Оценивание
параметров процесса контролируемого процесса в предположении нормальности
закона распределения
1. Оценивание параметров
производственного процесса в пусковой период
2. Оценка уровня настройки
процесса
Общее выборочное среднее
Среднее значение выборочных медиан
Медиана средних выборочных значений
3. Оценка технологического
рассеяния
Общее выборочное стандартное отклонение с поправкой
Среднее значение выборочных стандартных отклонений с поправкой
Корень квадратный из средней выборочной дисперсии с поправкой
Среднее значение размахов выборок с поправкой
Медиана размахов выборок с поправкой
Таблица 1. Коэффициенты для вычисления несмещенных оценок параметров и их дисперсий
См. также: Прикладная
математическая статистика (материалы к семинарам)
1. Оценивание параметров производственного процесса в пусковой
период
Во время пускового периода из текущего производства
для контролируемого показателя ![]() извлекаются выборки
извлекаются выборки ![]() ;
; ![]() .
.
Среднее значение, медиана, дисперсия, стандартное
отклонение и размах ![]() -й выборки
(
-й выборки
(![]() ) определяются соотношениями:
) определяются соотношениями:
![]() ,
(1)
,
(1)
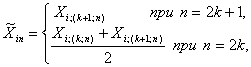 (2)
(2)
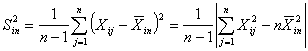 ,
(3)
,
(3)
![]() ,
(4)
,
(4)
![]() ,
(5)
,
(5)
где
![]() -
- ![]() -й элемент вариационного
ряда (упорядоченной
-й элемент вариационного
ряда (упорядоченной ![]() -й
выборки), построенного по
-й
выборки), построенного по ![]() -й выборке.
-й выборке.
Среднее значение выборочных средних, среднее значение выборочных медиан, среднее значение выборочных дисперсий, среднее значение выборочных стандартных отклонений и среднее значение выборочных размахов выборок:
![]() ,
(6)
,
(6)
![]() ,
(7)
,
(7)
![]() ,
(8)
,
(8)
![]() ,
(9)
,
(9)
![]() ,
(10)
,
(10)
Медиана выборочных средних, выборочных медиан, и выборочных размахов:
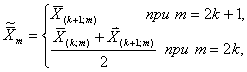 (11)
(11)
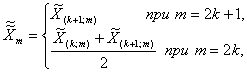 (12)
(12)
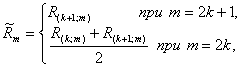 (13)
(13)
где
![]() -
- ![]() -й элемент в возрастающей
последовательности
-й элемент в возрастающей
последовательности ![]() выборочных средних
выборочных средних ![]() (в вариационном ряду). Аналогично
определяются
(в вариационном ряду). Аналогично
определяются ![]() и
и ![]() .
.
Оценки по всем выборкам определяем как общее выборочное среднее значение, общая выборочная дисперсия, общее выборочное стандартное отклонение:
![]() ,
(14)
,
(14)
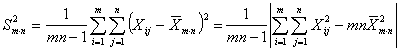 ,
(15)
,
(15)
![]() .
(16)
.
(16)
Через общую сумму квадратов отклонений
![]() (17)
(17)
общая выборочная дисперсия имеет вид
![]() .
(18)
.
(18)
2. Оценка уровня настройки процесса
Если уровень настройки процесса ![]() заранее неизвестен, то можно определить его
оценку, опираясь на данные, полученные в фазе пуска процесса. Для этого можно воспользоваться различными оценками для
заранее неизвестен, то можно определить его
оценку, опираясь на данные, полученные в фазе пуска процесса. Для этого можно воспользоваться различными оценками для ![]() . Рассматриваемые оценки являются
несмещенными и, по крайней мере, асимптотически нормально распределенными. Они имеют разные дисперсии, то есть отличаются по
эффективности.
. Рассматриваемые оценки являются
несмещенными и, по крайней мере, асимптотически нормально распределенными. Они имеют разные дисперсии, то есть отличаются по
эффективности.
Общее выборочное среднее ![]() имеет в качестве математического ожидания
имеет в качестве математического ожидания ![]() и дисперсию
и дисперсию
![]() ,
(19)
,
(19)
где
![]() – дисперсия процесса. Оценка подчиняется
нормальному закону, если нормальному закону подчиняются
– дисперсия процесса. Оценка подчиняется
нормальному закону, если нормальному закону подчиняются ![]() .
.
Медиана выборочных медиан. Медианы
отдельных выборок ![]() при нормально
распределенных
при нормально
распределенных ![]() распределены с математическим ожиданием
распределены с математическим ожиданием ![]() и дисперсией
и дисперсией
![]() .
(20)
.
(20)
Медиана ![]() выборочных медиан приблизительно нормально
распределена с математическим ожиданием
выборочных медиан приблизительно нормально
распределена с математическим ожиданием ![]() и дисперсией
и дисперсией
![]() .
(21)
.
(21)
Значения всех коэффициентов, встречающихся в соотношениях табулированы (таблица 1).
Среднее значение выборочных медиан ![]() имеет почти нормальное распределение с
математическим ожиданием
имеет почти нормальное распределение с
математическим ожиданием ![]() и дисперсией
и дисперсией
![]() .
(22)
.
(22)
Медиана средних выборочных значений ![]() распределена почти нормально с математическим
ожиданием
распределена почти нормально с математическим
ожиданием ![]() и дисперсией
и дисперсией
![]() .
(23)
.
(23)
При
![]() ,
, ![]() при
при ![]() и
и ![]() , поэтому
, поэтому
![]() <
< ![]() <
< ![]() <
< ![]() .
.
Наибольшей эффективностью из
рассмотренных оценок обладает общее среднее ![]() , наибольшей устойчивостью –
, наибольшей устойчивостью – ![]() .
.
3. Оценка технологического рассеяния
Технологическое рассеяние ![]() подлежит оцениванию по результатам исследования
пускового периода производственного процесса, если оно не известно заранее. Для
этого можно воспользоваться различными оценками для
подлежит оцениванию по результатам исследования
пускового периода производственного процесса, если оно не известно заранее. Для
этого можно воспользоваться различными оценками для ![]() . Рассматриваемые оценки
являются несмещенными (с использованием поправок). Оценки различаются
дисперсиями, то есть отличаются по эффективности.
. Рассматриваемые оценки
являются несмещенными (с использованием поправок). Оценки различаются
дисперсиями, то есть отличаются по эффективности.
Общее выборочное стандартное отклонение с поправкой.
Оценка (18) ![]() является несмещенной оценкой для
является несмещенной оценкой для ![]() . Однако
. Однако ![]() не является несмещенной
оценкой для стандартного отклонения
не является несмещенной
оценкой для стандартного отклонения ![]() . Несмещенной оценкой для стандартного отклонения
. Несмещенной оценкой для стандартного отклонения ![]() является оценка
является оценка
![]() ,
(24)
,
(24)
(![]() – табулировано) с дисперсией
– табулировано) с дисперсией
![]() ,
(25)
,
(25)
Среднее значение выборочных стандартных отклонений с
поправкой. Все ![]() стандартных отклонений, вычисляемые по
соотношению (4)
стандартных отклонений, вычисляемые по
соотношению (4) ![]() при
нормально распределенных
при
нормально распределенных ![]() имеют математическое ожидание
имеют математическое ожидание ![]() и дисперсию
и дисперсию
![]() ,
, ![]() .
(26)
.
(26)
Исправленное среднее значение выборочных стандартных отклонений дает несмещенную оценку
![]() ,
(27)
,
(27)
с дисперсией
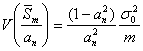 .
(28)
.
(28)
Корень квадратный из средней выборочной дисперсии с поправкой. Оценка
![]() (29)
(29)
имеет дисперсию
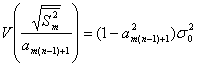 .
(30)
.
(30)
Среднее значение размахов выборок с поправкой. Все ![]() размахов
размахов ![]() в отдельных выборках при
нормально распределенных
в отдельных выборках при
нормально распределенных ![]() имеют математическое ожидание
имеют математическое ожидание ![]() и дисперсию
и дисперсию
![]() ,
, ![]() .
(31)
.
(31)
Несмещенная оценка стандартного отклонения
![]() (32)
(32)
имеет дисперсию
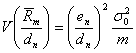 .
(33)
.
(33)
Медиана размахов выборок с поправкой. Вместо ![]() в качестве оценки можно
использовать медиану размахов выборки с поправкой
в качестве оценки можно
использовать медиану размахов выборки с поправкой
![]() ,
(34)
,
(34)
которая имеет дисперсию
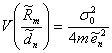 .
(35)
.
(35)
Все использованные выше коэффициенты табулированы (таблица 1).
Для
дисперсий данных оценок при ![]() справедливо неравенство:
справедливо неравенство:
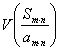 <
< 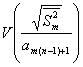 <
< 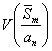 <
< 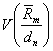 <
< 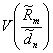 .
.
Таблица 1. Коэффициенты для вычисления несмещенных оценок параметров и их дисперсий
|
n |
cn |
an |
bn |
bn / an |
dn |
en |
en / dn |
|
|
|
2 |
1.000 |
0.798 |
0.603 |
0.756 |
1.128 |
0.853 |
0.756 |
0.954 |
0.450 |
|
3 |
1.160 |
0.886 |
0.463 |
0.523 |
1.693 |
0.888 |
0.525 |
1.588 |
0.435 |
|
4 |
1.092 |
0.921 |
0.389 |
0.422 |
2.059 |
0.880 |
0.427 |
1.978 |
0.445 |
|
5 |
1.198 |
0.940 |
0.341 |
0.363 |
2.326 |
0.864 |
0.371 |
2.257 |
0.457 |
|
6 |
1.136 |
0.952 |
0.308 |
0.324 |
2.534 |
0.848 |
0.335 |
2.472 |
0.468 |
|
7 |
1.214 |
0.959 |
0.282 |
0.294 |
2.704 |
0.833 |
0.308 |
2.645 |
0.447 |
|
8 |
1.159 |
0.965 |
0.262 |
0.272 |
2.847 |
0.820 |
0.288 |
2.791 |
0.487 |
|
9 |
1.223 |
0.969 |
0.246 |
0.254 |
2.970 |
0.808 |
0.272 |
2.915 |
0.495 |
|
10 |
1.175 |
0.973 |
0.232 |
0.238 |
3.078 |
0.797 |
0.259 |
3.024 |
0.503 |
|
11 |
1.229 |
0.975 |
0.221 |
0.227 |
3.173 |
0.787 |
0.248 |
3.121 |
0.509 |
|
12 |
1.190 |
0.978 |
0.211 |
0.216 |
3.258 |
0.778 |
0.239 |
3.207 |
0.515 |
|
13 |
1.233 |
0.979 |
0.202 |
0.206 |
3.336 |
0.770 |
0.231 |
3.285 |
0.521 |
|
14 |
1.195 |
0.981 |
0.194 |
0.198 |
3.407 |
0.762 |
0.224 |
3.356 |
0.527 |
|
15 |
1.237 |
0.982 |
0.187 |
0.190 |
3.472 |
0.755 |
0.217 |
3.422 |
0.532 |
|
16 |
1.202 |
0.983 |
0.181 |
0.184 |
3.532 |
0.749 |
0.212 |
3.482 |
|
|
17 |
1.238 |
0.985 |
0.175 |
0.178 |
3.588 |
0.743 |
0.207 |
3.538 |
|
|
18 |
1.207 |
0.985 |
0.170 |
0.173 |
3.640 |
0.738 |
0.203 |
3.591 |
|
|
19 |
1.239 |
0.986 |
0.165 |
0.167 |
3.689 |
0.733 |
0.199 |
3.640 |
|
|
20 |
1.212 |
0.987 |
0.161 |
0.163 |
3.735 |
0.729 |
0.195 |
3.686 |
|
|
¥ |
1.253 |
1 |
0 |
0 |
- |
- |
- |
- |
|