Определения. 1

Вопросы проверки гипотез о согласии по цензурированным выборкам. 2

Критерии Реньи. 2

Критерии типа Колмогорова-Смирнова. 4

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СТАТИСТИК КРИТЕРИЕВ РЕНЬИ И КОЛМОГОРОВА ПО ЦЕНЗУРИРОВАННЫМ ВЫБОРКАМ.. 6

Исследование распределений статистики Реньи при проверке простых гипотез о согласии по цензурированным выборкам. 7

Случай цензурирования I типа. 7

Случай цензурирования II типа. 12

Построение модифицированной статистики Реньи в случае цензурирования I типа 18

Исследование распределений статистики критерия Колмогорова при проверке простых гипотез о согласии по цензурированным выборкам. 21

Исследование распределений статистики Колмогорова по цензурированным выборкам при проверке сложных гипотез о согласии. 25

Определения

Определение 4. Выборка называется цензурированной справа (или слева) типа I в точке  (или ), если наблюдаются лишь те члены независимой выборки , значения которых принадлежат подмножеству  (или ) действительной прямой.

Определение 5. Выборка называется цензурированной справа (или слева) типа II, если наблюдаются лишь  наименьших (или  наибольших) членов вариационного ряда, построенного по выборке , , .

В случае цензурирования I типа, по сути, фиксируются вероятности попадания в интервалы цензурирования  и , а  и  обозначают случайное число наблюдений, попавших в интервалы цензурирования. При II типе количество цензурированных наблюдений  и  известно, а граничные точки  и  случайны. В таком случае в качестве  обычно выбирают наименьшее наблюдаемое значение, а в качестве  - наибольшее.

Определение 6. Степенью цензурирования  будем называть вероятность попадания в интервал цензурирования в случае цензурирования I типа, или отношение количества цензурированных наблюдений к полному объему выборки в случае цензурирования II типа.

С цензурированными выборками чаще всего сталкиваются при статистическом анализе данных типа времени жизни. Это могут быть наблюдения, полученные в ходе исследований в биологии и медицине или результаты испытаний на надежность некоторых технических систем, когда эксперимент проходит в условиях ограниченности по времени (цензурирование I типа) или по количеству наблюдений (цензурирование II типа).

Вопросы проверки гипотез о согласии по цензурированным выборкам

Критерии Реньи.

Статистики критерия Реньи, применяемого для проверки простой непараметрической гипотезы , согласно которой независимые одинаково распределенные случайные величины  имеют заданную непрерывную функцию распределения , задаются следующими выражениями [64, 70]:

– в случае цензурирования слева ():

,

,

;

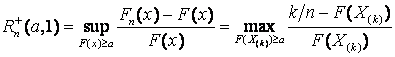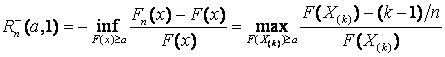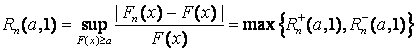– в случае цензурирования справа ():

,

,

,

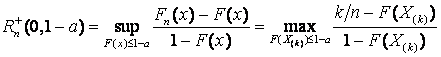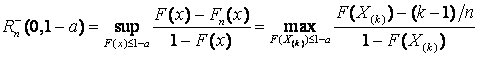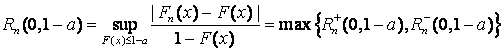где  – любое фиксированное число из промежутка (0, 1), отражающее, по сути, степень цензурирования. Если имеет место цензурирование I типа (см. определение 4), то  – при цензурировании слева или  – при цензурировании справа; в случае цензурирования II типа (см. определение 5)  – при цензурировании слева или  – при цензурировании справа.  – члены вариационного ряда , построенного по наблюдениям .

Случайные величины , ,  и  распределены одинаково (аналогичное утверждение справедливо и для статистик  и ) и, как показал Реньи [38], имеют место предельные соотношения:

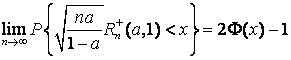,                               (1.10)

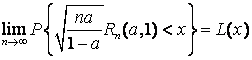,  ,                             (1.11)

где  – функция стандартного нормального распределения,  – функция распределения Реньи:

.

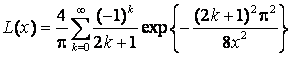Для статистик , ,  и  в [23, 135] получены точные распределения.

Критерии типа Колмогорова-Смирнова.

Для проверки согласия эмпирического распределения  с теоретическим  по цензурированным данным также могут использоваться критерии типа Колмогорова-Смирнова. Статистики Колмогорова-Смирнова определяются следующими выражениями [114]:

– в случае цензурирования слева:

, ,

– в случае цензурирования справа:

, ,

,

где  – степень цензурирования (вероятность попадания в интервал цензурирования в случае I типа или отношение количества цензурированных наблюдений к потенциальному объему выборки в случае II типа цензурирования). Точнее: ,  – статистики Смирнова,  – статистика Колмогорова.

На практике статистику Колмогорова удобнее вычислять следующим образом [64]:

,

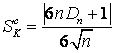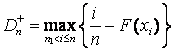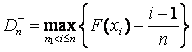где  и ,  – в случае цензурирования слева, 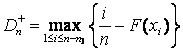,  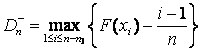– в случае цензурирования справа, где  и  – количество наблюдений, попавших в левый или правый интервал цензурирования, соответственно.

В работах [2, 114] выведено предельное соотношение:

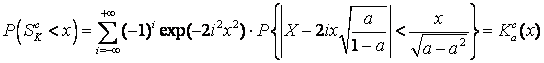,    (1.12)

где  – случайная величина, подчиненная стандартному нормальному закону. При  предельное распределение статистики  совпадает с классическим распределением Колмогорова (для случая полной выборки):

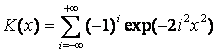.                                   (1.13)

В [29] приведена таблица процентных точек для распределения  при различных значениях степени цензурирования . В [135] получено точное распределение для статистик Смирнова (см. также [22, 76]).

Отметим еще раз, что применение перечисленных выше критериев предполагает проверку простых гипотез . Однако в практике статистического анализа очень часто приходится сталкиваться с необходимостью проверки гипотез о согласии после оценивания по этой же выборке параметров предполагаемого закона распределения. К сожалению, в отличие от критериев согласия типа , непараметрические критерии типа Реньи и Колмогорова в случае проверки сложных гипотез теряют свойство “свободы от распределения”. Распространенная ошибка, связанная с пренебрежением существующей проблемы, когда при проверке сложной гипотезы пользуются предельными распределениями, полученными для случая простой гипотезы, чаще всего приводит к необоснованному принятию нулевой гипотезы.

Для случая проверки сложных гипотез о согласии по полным выборкам, когда исследователю доступны все индивидуальные наблюдения, в литературе описаны различные подходы к решению данной проблемы. Если объем выборки достаточно велик, можно, опираясь на результаты, полученные в [12], оценивать параметры распределения по одной половине, а проверять согласие – по другой. В [147–149] для статистик типа Колмогорова-Смирнова и некоторых законов, соответствующих гипотезе , получены формулы для приближенного вычисления вероятностей «согласия» вида , где  – вычисленное по выборке значение соответствующей статистики . Построенные формулы дают достаточно хорошие приближения при малых значениях соответствующих вероятностей. Однако в случае цензурированных выборок этот подход неприменим. Существует совершенно иной подход, основанный на статистическом моделировании. Для заданного закона распределения в зависимости от того, какие параметры оцениваются и какой метод оценивания используется, моделируется эмпирическое распределение статистики и проводится процедура идентификации полученного распределения [93].

Теоретически статистики типа Реньи имеют то преимущество, что предельные распределения этих статистик в случае проверки простых гипотез не зависят от степени цензурирования, и по идее, такими критериями удобнее пользоваться на практике. Однако вопрос о том, насколько хорошо распределения статистик Реньи согласуются с соответствующими предельными законами при ограниченных объемах выборок, до сих пор не исследовался. Неизвестно и то, насколько быстро сходятся к своим предельным законам распределения статистики Колмогорова в случае цензурированных выборок.

В 5 главе данной работы исследуются распределения статистик типа Реньи и Колмогорова при проверке простых и сложных гипотез о согласии, моделируются законы распределения, аппроксимирующие предельные распределения статистики Колмогорова  при проверке сложных гипотез и использовании ОМП по цензурированным данным.

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СТАТИСТИК КРИТЕРИЕВ РЕНЬИ И КОЛМОГОРОВА ПО ЦЕНЗУРИРОВАННЫМ ВЫБОРКАМ

В данной главе исследуются распределения статистик типа Реньи и типа Колмогорова при проверке простых и сложных гипотез по цензурированным выборкам в зависимости от степени цензурирования. Строятся аппроксимации предельных распределений статистики Колмогорова при проверке сложных гипотез с использованием ОМП по цензурированным выборкам.

Результаты исследований, представленные в данной главе, опубликованы в [103, 109, 151].

Исследование распределений статистики Реньи при проверке простых гипотез о согласии по цензурированным выборкам

Случай цензурирования I типа

Целью настоящего раздела является исследование сходимости распределений статистик Реньи к соответствующим предельным законам при различной величине наблюдаемой области в случае одностороннего цензурирования I типа, когда фиксируется вероятность попадания в интервал цензурирования, а число наблюдений, попавших в интервал цензурирования, случайно. Другими словами, необходимо выяснить, начиная с какого объема выборки при проверке простой гипотезы о согласии можно пользоваться предельными соотношениями (1.5) и (1.6). В случае I типа цензурирования в выражениях для статистик Реньи  – это вероятность попадания наблюдения в интервал цензурирования.

Для этого моделировались и исследовались эмпирические распределения статистик Реньи при различных проверяемых гипотезах. По каждому закону распределения  моделировалась серия из  выборок объемом . Для каждой выборки проводилась процедура цензурирования (слева или справа), после чего по ней вычислялось значение статистики Реньи. Ниже приводятся результаты моделирования и анализа, которые позволяют сделать определенные выводы.

Предельным распределением статистик  и  (двустороннего критерия Реньи) является распределение  (1.6).

На рис. 5.1 приведены эмпирические распределения статистики  для случая проверки простой гипотезы о согласии с экспоненциальным законом с параметром масштаба  по цензурированным слева выборкам, с вероятностью попадания в интервал цензурирования . Из рисунка видно, что при такой степени цензурирования даже при потенциальном (полном) объеме выборки  (в этом случае количество наблюдаемых значений в выборке около 100) эмпирическое распределение статистики Реньи существенно отличается от предельного закона .

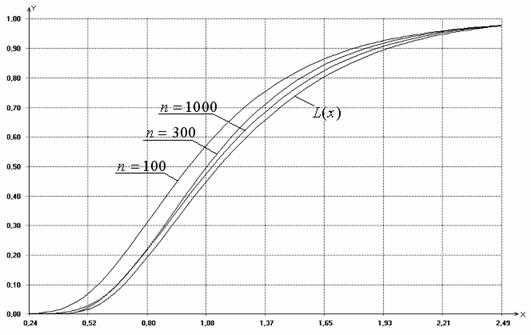
Рис. 5.1. Распределения статистики  при 10% наблюдаемой области

(), цензурирование слева, I тип

Рис. 5.2 иллюстрирует зависимость распределений статистики  от степени цензурирования. Из рисунка видно, что наилучшее согласие с предельным распределением  достигается при 50% наблюдаемой области определения случайной величины, а при малой или, наоборот, высокой степени цензурирования распределения статистики существенно отличаются от предельного.

Необходимо отметить, что в случаях проверки согласия с другими законами распределения, прослеживаются те же закономерности.

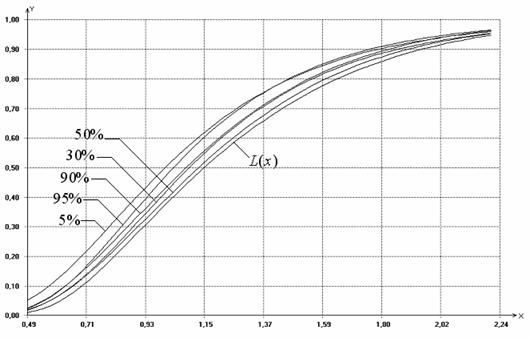
Рис. 5.2. Распределения статистики, , цензурирование слева, I типа при различной величине наблюдаемой области, %

Для уточнения анализа сходимости распределений статистик  и  к предельному распределению  рассмотрим в качестве меры близости эмпирического распределения статистики Реньи с  статистику Колмогорова . То есть, используя критерий согласия Колмогорова, будем проверять простую гипотезу о согласии вида:

 – в случае цензурирования слева,                    (5.1)

 – в случае цензурирования справа,             (5.2)

где  и  – эмпирические функции распределения статистик  и  при условии, что верна основная гипотеза ,  – количество выборок наблюдений случайной величины из распределения  (объем выборки статистик). Статистику Колмогорова удобнее вычислять следующим образом [64]:

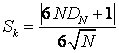,                                                 (5.3)

где ,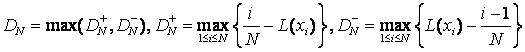

 – упорядоченные по возрастанию значения рассматриваемой статистики Реньи.

Вычисляя значения статистики Колмогорова, можно для конкретных объемов выборки  и степени цензурирования  определить достигаемый уровень значимости , т.е. вероятность истинности гипотез (5.1) и (5.2) , где  – распределение Колмогорова (1.13). Рассмотрим в качестве  экспоненциальное распределение с параметром масштаба , .

В таблице 5.1 представлены значения статистики Колмогорова при проверке гипотезы (5.1) и соответствующие вероятности истинности данной гипотезы (достигаемый уровень значимости). Для того, чтобы можно было сделать вывод об общей закономерности, каждое значение статистики Колмогорова усреднялось по 100 экспериментам. В таблице 5.2 представлены аналогичные значения, но для случая проверки гипотезы (5.2). Гипотезы (5.1) и (5.2) различаются только тем, что в первом случае выборка наблюдений цензурируется слева, а во втором случае – справа.

Таблица 5.1

Значения статистики Колмогорова при проверке гипотезы (5.1) и соответствующие достигаемые уровни значимости

0,95	4,76	0,00	2,93	0,00	2,39	0,00	1,98	0,00
0,9	2,92	0,00	2,09	0,00	1,81	0,00	1,60	0,01
0,8	2,01	0,00	1,52	0,02	1,47	0,03	1,26	0,09
0,7	1,74	0,00	1,36	0,05	1,32	0,06	1,18	0,12
0,6	1,61	0,01	1,31	0,06	1,22	0,10	1,14	0,15
0,5	1,56	0,02	1,28	0,08	1,17	0,13	1,14	0,15
0,4	1,57	0,01	1,24	0,09	1,17	0,13	1,15	0,14
0,3	1,56	0,02	1,24	0,09	1,19	0,12	1,11	0,17
0,2	1,72	0,01	1,43	0,03	1,30	0,07	1,23	0,09
0,1	2,15	0,00	1,69	0,01	1,49	0,02	1,36	0,05
0,05	3,09	0,00	2,18	0,00	1,88	0,00	1,55	0,02

Таблица 5.2

Значения статистики Колмогорова при проверке гипотезы (5.2) и соответствующие достигаемые уровни значимости

0,95	4,75	0,00	2,89	0,00	2,35	0,00	1,85	0,00
0,9	2,86	0,00	1,98	0,00	1,72	0,01	1,48	0,02
0,8	2,02	0,00	1,50	0,02	1,39	0,04	1,32	0,06
0,7	1,81	0,00	1,43	0,03	1,30	0,07	1,22	0,10
0,6	1,63	0,01	1,31	0,06	1,23	0,10	1,16	0,14
0,5	1,56	0,02	1,27	0,08	1,23	0,10	1,17	0,13
0,4	1,45	0,03	1,26	0,08	1,17	0,13	1,18	0,12
0,3	1,52	0,02	1,31	0,06	1,21	0,11	1,11	0,17
0,2	1,68	0,01	1,39	0,04	1,31	0,06	1,17	0,13
0,1	2,09	0,00	1,74	0,00	1,50	0,02	1,36	0,05
0,05	3,04	0,00	2,24	0,00	1,93	0,00	1,63	0,01

Сравнивая соответствующие значения в табл. 5.1 и 5.2, несложно заметить, что эти значения практически совпадают, т.е. распределения статистики Реньи не зависят от того, является ли выборка цензурированной слева или справа.

Как видно из таблиц 5.1 и 5.2, при значительной степени цензурирования (), а также, наоборот, когда вероятность попадания в наблюдаемую область близка к единице (), вероятность принять гипотезу  не достигает даже значения . Это говорит о том, что в этом случае при уровне значимости, равном  гипотезы о согласии (5.1) и (5.2) отвергаются, т.е. эмпирические распределения статистик  и  не согласуются с предельным распределением . При степени цензурирования  вероятность истинности  гипотезы  достигает значения  при объеме выборки  и если  – при .

Таким образом, достаточно хорошее согласие эмпирических распределений статистики Реньи с предельным законом  в случае цензурирования I типа достигается лишь при  и вероятности попадания в интервал цензурирования, близкой к 0,5. Аналогичные закономерности прослеживаются и при проверке согласия с другими законами распределения.

Полученные результаты, вообще говоря, указывают на то, что при ограниченных объемах выборки () критерий Реньи для проверки согласия цензурированной I типа выборки с некоторым теоретическим распределением неприменим.

Случай цензурирования II типа

В данном разделе исследуется сходимость распределений статистик Реньи к соответствующим предельным законам при различной величине наблюдаемой области в случае одностороннего цензурирования II типа, когда фиксируется количество наблюдений, а вероятность попадания в интервал цензурирования и, соответственно, граничная точка – случайны. В этом случае в выражениях для статистик Реньи величина  – это отношение количества наблюдений, попадающих в интервал цензурирования к общему объему выборки:  в случае цензурирования слева или  в случае цензурирования справа.

На рис. 5.3 представлены эмпирические распределения статистики  (цезурирование слева, II тип) при объемах выборки ,  при проверке простой гипотезы о согласии с экспоненциальным законом с параметром масштаба . При II типе цензурирования графики эмпирических распределений статистики Реньи пересекают график предельного закона распределения .

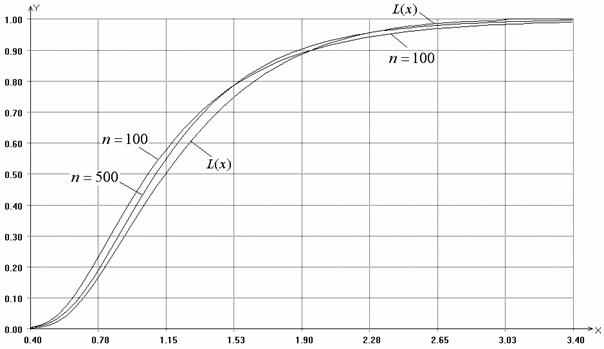
Рис. 5.3. Распределения статистики  при 10% наблюдаемой области,

цензурирование слева, II тип

Несмотря на то, что эмпирические распределения статистики Реньи при I и II типах цензурирования имеют существенные отличия по форме, скорость сходимости распределения статистики Реньи к предельному закону  с ростом объема выборки при I и II типе совпадают. В этом несложно убедиться, сравнивая соответствующие значения таблицы 5.1 и таблицы 5.3, в которой представлены усредненные по 100 экспериментам значения статистики Колмогорова, полученные при проверке гипотезы (5.1) при тех же условиях, что и в таблице 5.1, но в случае цензурирования II типа.

В таблице 5.4 представлены значения статистики Колмогорова, полученные при проверке гипотезы (5.2). Эти значения получены аналогично случаю, представленному в табл. 5.2, но при II типе цензурирования.

Таблица 5.3

Значения статистики Колмогорова при проверке гипотезы (5.1) и соответствующие достигаемые уровни значимости

0,95	3,24	0,00	2,39	0,00	2,06	0,00	1,83	0,00
0,9	2,43	0,00	1,90	0,00	1,68	0,01	1,54	0,02
0,8	1,88	0,00	1,47	0,03	1,44	0,03	1,24	0,09
0,7	1,67	0,01	1,34	0,05	1,31	0,06	1,16	0,13
0,6	1,59	0,01	1,26	0,08	1,21	0,11	1,15	0,15
0,5	1,54	0,02	1,25	0,09	1,18	0,12	1,13	0,16
0,4	1,59	0,01	1,29	0,07	1,18	0,13	1,16	0,14
0,3	1,71	0,01	1,30	0,07	1,22	0,10	1,13	0,15
0,2	1,97	0,00	1,49	0,02	1,35	0,05	1,23	0,10
0,1	2,68	0,00	1,96	0,00	1,69	0,01	1,43	0,03
0,05	4,15	0,00	2,71	0,00	2,20	0,00	1,74	0,00

Таблица 5.4

Значения статистики Колмогорова при проверке гипотезы (5.2) и соответствующие достигаемые уровни значимости

0,95	3,17	0,00	2,33	0,00	2,13	0,00	1,84	0,00
0,9	2,46	0,00	2,01	0,00	1,79	0,00	1,64	0,01
0,8	1,90	0,00	1,40	0,04	1,44	0,03	1,40	0,04
0,7	1,64	0,01	1,55	0,02	1,35	0,05	1,30	0,07
0,6	1,60	0,01	1,42	0,03	1,32	0,06	1,05	0,22
0,5	1,67	0,01	1,22	0,10	1,32	0,06	1,16	0,14
0,4	1,69	0,01	1,39	0,04	1,36	0,05	1,08	0,19
0,3	1,73	0,01	1,41	0,04	1,25	0,09	1,11	0,17
0,2	1,94	0,00	1,38	0,04	1,47	0,03	1,25	0,09
0,1	2,67	0,00	1,79	0,00	1,82	0,00	1,51	0,02
0,05	4,16	0,00	2,85	0,00	2,53	0,00	1,87	0,00

Если сравнивать полученные результаты при цензурировании слева и справа, т.е. сравнить значения в табл. 5.3 и 5.4, то можно заметить, что, в целом, отличия несущественные, но небольшая разница все же наблюдается: в случае цензурирования справа закономерности прослеживаются менее четко и эмпирические распределения статистики Реньи сходятся к предельному закону  медленнее, чем при цензурировании слева. Объясняется это тем, что правый «хвост» экспоненциального распределения содержит гораздо больше информации о распределении, чем левый и поэтому разброс значений статистики Реньи при цензурировании справа шире, чем в аналогичной ситуации, но при цензурировании слева.

Различия между эмпирическими распределениями статистики Реньи и предельным законом при II типе цензурирования обусловлены не только формой распределения, но и существенным различием в масштабе, в отличие от случая цензурирования I типа. Так как параметр  входит в выражение для статистики Реньи в качестве масштабирующего множителя, то можно попытаться изменить статистику Реньи следующим образом: при вычислении статистики для каждой выборки наблюдений в качестве значения  брать вероятность попадания в интервал цензурирования, а не заданное изначально отношение числа наблюдений в интервале цензурирования к потенциальному объему выборки. Понятно, что от выборки к выборке при II типе цензурирования значение вероятности будет меняться, т.к. в этом случае в качестве граничной точки выбирается последнее (при цензурировании справа) или первое (при цензурировании слева) наблюдаемое выборочное значение. Так как предельное распределение статистики  от  не зависит, то такое изменение правомерно. В таблицах 5.5 и 5.6 представлены значения статистики Колмогорова при проверке гипотезы  при цензурировании слева и справа соответственно, а величина  в выражении для статистики Реньи вычислялась как вероятность попадания в интервал цензурирования.

Таблица 5.5

Значения статистики Колмогорова при проверке гипотезы (5.1) и соответствующие достигаемые уровни значимости

0,95	1,26	0,08	1,33	0,06	1,35	0,05	1,40	0,04
0,9	1,32	0,06	1,33	0,06	1,29	0,07	1,32	0,06
0,8	1,18	0,12	1,13	0,16	1,22	0,10	1,11	0,17
0,7	1,13	0,15	1,08	0,20	1,15	0,14	1,06	0,21
0,6	1,09	0,18	1,07	0,20	1,07	0,20	1,07	0,20
0,5	1,07	0,20	1,03	0,24	1,03	0,24	1,06	0,21
0,4	1,09	0,19	1,04	0,23	1,03	0,24	1,06	0,21
0,3	1,07	0,20	1,00	0,27	1,01	0,26	1,00	0,27
0,2	1,05	0,22	1,04	0,22	1,06	0,21	1,07	0,21
0,1	1,05	0,22	1,10	0,18	1,12	0,16	1,11	0,17
0,05	1,20	0,11	1,11	0,17	1,12	0,17	1,08	0,19

Таблица 5.6

Значения статистики Колмогорова при проверке гипотезы (5.2) и соответствующие достигаемые уровни значимости

0,95	1,29	0,07	1,32	0,06	1,36	0,05	1,32	0,06
0,9	1,27	0,08	1,31	0,07	1,21	0,11	1,19	0,12
0,8	1,25	0,09	1,18	0,12	1,18	0,12	1,17	0,13
0,7	1,17	0,13	1,14	0,15	1,10	0,18	1,11	0,17
0,6	1,14	0,15	1,06	0,22	1,05	0,22	1,07	0,21
0,5	1,10	0,18	1,01	0,26	1,08	0,19	1,07	0,21
0,4	1,00	0,27	1,07	0,20	1,05	0,22	1,07	0,20
0,3	1,00	0,27	1,02	0,25	1,03	0,24	1,05	0,22
0,2	0,99	0,28	1,03	0,24	1,10	0,18	1,03	0,24
0,1	1,00	0,27	1,05	0,22	1,12	0,16	1,07	0,20
0,05	1,19	0,12	1,09	0,19	1,17	0,13	1,15	0,14

Как видно из таблиц 5.5 и 5.6, если параметр  в выражении для статистики Реньи вычислять как вероятность попадания в интервал цензурирования, то при II типе цензурирования скорость сходимости эмпирических распределений статистики Реньи к предельному закону существенно выше, чем если в качестве  брать фиксированную величину  при цензурировании слева или  при цензурировании справа. Уже при потенциальном объеме выборки  и степени цензурирования , при  и  наблюдается хорошее согласие эмпирических распределений статистики Реньи с . При высокой степени цензурирования  вероятности истинности гипотезы  выше, чем соответствующие вероятности в таблицах 5.3 и 5.4, но все же разница между эмпирическими распределениями статистики Реньи и предельным законом существенная.

В качестве примера на рисунке 5.4 приведены эмпирические распределения статистики Реньи при проверке согласия с распределением Вейбулла с параметром масштаба  и параметром формы  в случае цензурирования слева, II тип, при величине наблюдаемой области 5%, 10% и 30%, . Из рисунка видно, что при 5% наблюдаемой области отличие между эмпирическим распределением статистики Реньи и  существенно, при 10% - различие по-прежнему заметно, но уже не столь существенно, а при 30% наблюдаемой области визуально уже трудно различить эмпирическое распределение от предельного.

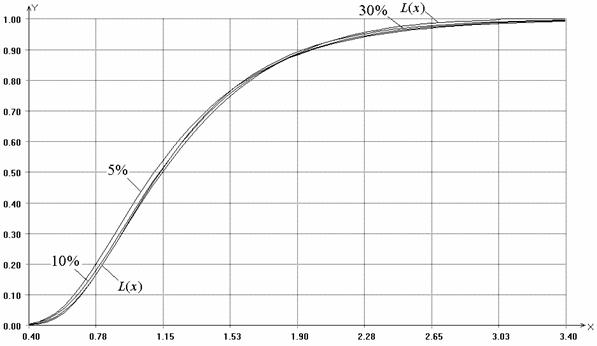
Рис. 5.4. Распределения статистики  при ,

цензурирование слева, II тип

Построение модифицированной статистики Реньи в случае цензурирования I типа

Анализ полученных результатов наталкивает на мысль о том, что можно ввести некоторую поправку, обратно пропорциональную объему выборки, в выражениях для статистик Реньи так, чтобы распределения модифицированной статистики быстрее сходились к предельному закону . Введем поправку  следующим образом:

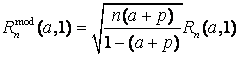.                                  (5.4)

Будем искать оценку  как решение оптимизационной задачи

,                                 (5.5)

где  – эмпирическая функция распределения статистики , получаемая при моделировании выборки объема  значений этой статистики в случае проверки простой гипотезы ,  – предельное распределение Реньи (1.6). Минимизируемый функционал представляет собой статистику Колмогорова. Введем обозначение: . Так как функционал  не является унимодальным, т.е. имеет множество локальных экстремумов, но в то же время из способа введения поправки  (5.4) понятно, что , будем искать решение задачи (5.5) простым перебором на промежутке . Значения  вычисляются в соответствии со следующим алгоритмом:

1. Моделируется выборка из распределения  объемом .

2. Проводится цензурирование полученной выборки I типа, слева при заданной степени цензурирования .

3. По цензурированной выборке вычисляется значение статистики .

4. Повторяя пункты 1-3  раз, получим выборку значений статистики .

5. По полученной выборке из значений статистики вычисляется статистика Колмогорова по формуле (5.3).

Функция  зависит не только от , но и от конкретной реализации выборочных значений. Поэтому необходимо начинать моделирование выборки значений статистики  с одного и того же начального значения датчика случайных чисел, т.е. будем находить  по некоторому фиксированному набору выборок. Таким образом, будем получать оптимальное значение  для некоторого одного эмпирического распределения статистики Реньи. Находя оптимальное значение поправки  для 100 различных реализаций эмпирического распределения статистики Реньи и вычисляя среднюю величину  по этим 100 экспериментам, получим оценку поправки  для конкретного объема выборки  и степени цензурирования .

Результаты поиска оптимального значения поправки  для случая экспоненциального распределения представлены в таблице 5.7. В последней строке таблицы приведены усредненные по степени цензурирования значения.

Таблица 5.7

Оценки поправки  к статистике Реньи в случае цензурирования I типа

	n=100	n=150	n=200	n=250	n=300	n=350	n=400
0,95	0,0126	0,0095	0,0072	0,0061	0,0056	0,0049	0,0047
0,9	0,0139	0,0112	0,0091	0,0075	0,0069	0,0065	0,0056
0,8	0,0144	0,0125	0,0105	0,0090	0,0094	0,0072	0,0074
0,7	0,0140	0,0122	0,0101	0,0104	0,0096	0,0090	0,0081
0,6	0,0123	0,0123	0,0118	0,0092	0,0101	0,0094	0,0088
0,5	0,0131	0,0122	0,0105	0,0100	0,0097	0,0087	0,0077
0,4	0,0135	0,0115	0,0112	0,0099	0,0092	0,0079	0,0075
0,3	0,0121	0,0104	0,0109	0,0095	0,0091	0,0087	0,0091
0,2	0,0128	0,0105	0,0110	0,0082	0,0071	0,0074	0,0061
0,1	0,0119	0,0080	0,0066	0,0070	0,0056	0,0049	0,0047
0,05	0,0090	0,0072	0,0059	0,0049	0,0048	0,0042	0,0037
среднее	0,0127	0,0107	0,0095	0,0083	0,0079	0,0072	0,0067

Анализируя полученные значения поправки , можно заметить, что при  значения  близки к средним величинам при конкретных объемах выборки, а при  значения  меньше средних примерно в 1,45 раза. Составим уравнение парной регрессии относительно зависимой переменной  и независимой переменной . После оценивания коэффициентов регрессии методом наименьших квадратов получена следующая оценка зависимости средних величин  от объема выборки:

.                               (5.6)

В таблицах 5.8 и 5.9 представлены усредненные по 100 экспериментам значения статистики Колмогорова, полученные для случая проверки гипотезы вида

,                                (5.7)

а также соответствующие значения достигнутого уровня значимости. В качестве  взято логнормальное распределение с параметром сдвига  и параметром масштаба , .

Таблица 5.8

Значения статистики Колмогорова при проверке гипотезы (5.7) в случае цензурирования слева и соответствующие достигаемые уровни значимости

	n=100		n=150		n=200		n=300		n=400		n=500
0,95	2,15	0,00	1,43	0,03	1,19	0,12	0,99	0,29	0,90	0,39	0,92	0,36
0,9	1,60	0,01	1,29	0,07	1,14	0,15	1,00	0,26	0,98	0,29	0,93	0,35
0,8	1,03	0,24	0,91	0,39	0,96	0,32	0,90	0,39	0,88	0,41	0,89	0,41
0,7	1,03	0,24	0,95	0,33	0,95	0,33	0,91	0,37	0,92	0,37	0,88	0,42
0,6	1,03	0,24	0,95	0,33	0,95	0,32	0,95	0,33	0,91	0,38	0,85	0,46
0,5	0,99	0,28	0,94	0,35	0,94	0,35	0,93	0,35	0,94	0,34	0,86	0,46
0,4	0,96	0,31	0,89	0,41	0,94	0,34	0,91	0,38	0,94	0,33	0,86	0,44
0,3	0,90	0,39	0,89	0,41	0,93	0,35	0,89	0,41	0,95	0,32	0,90	0,40
0,2	0,88	0,42	0,93	0,36	0,91	0,38	0,87	0,43	0,88	0,41	0,90	0,39
0,1	0,92	0,37	0,96	0,31	0,94	0,34	0,95	0,33	0,92	0,37	0,92	0,36
0,05	1,03	0,24	0,97	0,31	0,92	0,37	0,96	0,31	0,96	0,31	0,96	0,31

Таблица 5.9

Значения статистики Колмогорова при проверке гипотезы (5.7) в случае цензурирования справа и соответствующие достигаемые уровни значимости

	n=100		n=150		n=200		n=300		n=400		n=500
0,95	2,10	0,00	1,49	0,02	1,12	0,17	0,99	0,28	0,94	0,34	0,92	0,37
0,9	1,55	0,02	1,27	0,08	1,10	0,18	1,01	0,26	1,01	0,26	0,97	0,31
0,8	1,02	0,25	1,00	0,27	0,90	0,39	0,95	0,32	0,97	0,30	0,90	0,40
0,7	0,98	0,30	0,99	0,28	0,93	0,35	0,94	0,34	0,94	0,34	0,96	0,31
0,6	0,94	0,34	1,00	0,27	0,93	0,36	0,90	0,39	0,95	0,33	0,89	0,40
0,5	0,90	0,39	1,00	0,27	0,95	0,32	0,91	0,38	0,90	0,39	0,90	0,39
0,4	0,88	0,42	0,95	0,33	0,92	0,37	0,86	0,46	0,90	0,39	0,92	0,36
0,3	0,89	0,41	0,89	0,41	0,87	0,43	0,89	0,41	0,86	0,45	0,93	0,35
0,2	0,91	0,38	0,89	0,40	0,88	0,42	0,86	0,45	0,90	0,39	0,93	0,36
0,1	0,94	0,34	0,92	0,36	0,95	0,33	0,92	0,36	0,93	0,36	0,93	0,35
0,05	1,04	0,23	0,91	0,38	0,94	0,34	0,94	0,34	0,94	0,33	0,91	0,38

Как видно из табл. 5.8, 5.9, уже при потенциальном объеме выборки  для  и начиная с  для  распределения модифицированной статистики Реньи (5.4) с поправкой (5.6) при цензурировании I типа хорошо согласуются с предельным законом распределения .

Исследование распределений статистики критерия Колмогорова при проверке простых гипотез о согласии по цензурированным выборкам

Предельное распределение статистики Колмогорова в случае цензурированных выборок определяется выражением (1.7) и в отличие от предельного распределения Реньи зависит от степени цензурирования. Используя методику компьютерного моделирования и анализа статистических закономерностей, исследуем сходимость эмпирического распределения статистики Колмогорова к соответствующему предельному закону при различной величине наблюдаемой области. На рис. 5.5 представлены эмпирические функции распределения статистики Колмогорова при проверке простой гипотезы о согласии с экспоненциальным законом с параметром масштаба  при  и степени цензурирования , а также соответствующие предельные распределения статистики Колмогорова по цензурированным выборкам.

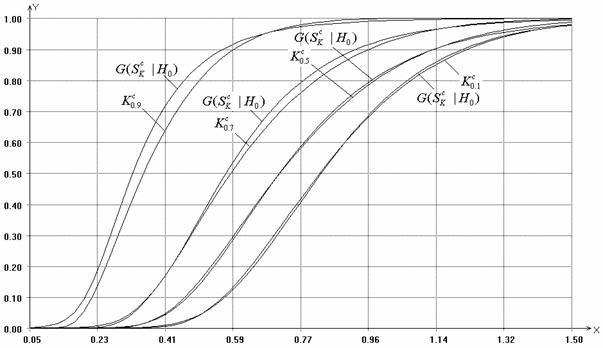
Рис. 5.5. Распределения статистики  при различной степени цензурирования и , цензурирование слева, I тип

Из рис. 5.5 видно, что уже при потенциальном объеме выборки  в случае  и ниже (т.е. при величине наблюдаемой части 50% от области определения случайной величины и выше) эмпирические распределения статистики Колмогорова хорошо согласуются с соответствующими предельными распределениями , а при величине наблюдаемой области меньше 30% наблюдается существенное отличие эмпирических распределений статистики  от соответствующих предельных законов.

Для более точного анализа согласованности эмпирических распределений статистики Колмогорова для цензурированных выборок как и при исследовании распределений статистики Реньи, рассмотрим задачу проверки гипотезы о согласии вида:

,                                             (5.8)

где  – эмпирическая функция распределения статистики  при верности основной гипотезы. Значения  вычисляются для случая проверки простой гипотезы ,  – количество выборок наблюдений случайной величины из распределения . Для проверки гипотез  снова воспользуемся критерием согласия Колмогорова (для полных выборок). 

  Как отмечается в [93], в случае полных (нецензурированных) выборок эмпирические распределения статистики Колмогорова уже при объеме выборки  хорошо согласуются с распределением Колмогорова. Рассмотрим степень согласованности эмпирических распределений статистики Колмогорова по цензурированным выборкам при . В таблице 5.10 представлены значения вероятности истинности гипотезы (5.8) (значения достигнутого уровня значимости)  для различной степени цензурирования . В качестве  взято экспоненциальное распределение, количество выборок .

Таблица 5.10

Значения достигнутого уровня значимости при проверке гипотезы (5.8)

	I тип, слева	I тип, справа	II тип, слева	II тип, справа
0,95	0,0000	0,0000	0,0000	0,0000
0,9	0,0000	0,0000	0,0031	0,0021
0,8	0,0000	0,0000	0,1043	0,0629
0,7	0,0062	0,0000	0,2419	0,1914
0,6	0,0818	0,0027	0,3054	0,2160
0,5	0,2213	0,0394	0,3310	0,2695
0,4	0,3416	0,1066	0,3498	0,2691
0,3	0,3920	0,1957	0,3275	0,2688
0,2	0,4020	0,2653	0,3350	0,3004
0,1	0,4071	0,3243	0,4035	0,3828
0,05	0,3959	0,3469	0,4237	0,4135

Как видно из таблицы 5.10, степень согласованности эмпирических распределений статистики Колмогорова с соответствующими предельными распределениями зависит от того, к какому типу цензурирования относится выборка. В случае цензурирования I типа при степени цензурировании  вероятность истинности гипотезы (5.8) превышает 0,2, что говорит о том, что распределения статистики Колмогорова действительно хорошо описываются предельным законом (1.7). При цензурировании I типа справа для случая экспоненциального распределения значения вероятностей  при проверке гипотезы (5.8) ниже, чем при цензурировании слева, и достигают величины 0,2 только при . Эта разница вновь объясняется тем, что правый «хвост» экспоненциального распределения содержит гораздо больше информации о распределении, чем левый. Если в качестве  при вычислении значений статистики  при проверке гипотезы (5.8) выбрать нормальное распределение, то никаких различий в результатах при цензурировании слева и справа не будет, т.к. это симметричное распределение.

Для несимметричных законов распределения исследуемой случайной величины при малых объемах выборки () распределения статистики Колмогорова зависят от того, с какой стороны (слева или справа) цензурируется выборка.

Таким образом, исследуя величины вероятности  при проверке гипотезы (5.8), находим минимальный объем выборки, при котором достигается хорошее согласие эмпирических распределений статистики Колмогорова с соответствующими предельными законами для различных типов цензурирования. Результаты представлены в таблице 5.11.

Таблица 5.11

Минимальный объем выборки, при котором достигаемый уровень значимости при проверке гипотезы (5.8) превышает 0,2

	I тип, слева	I тип, справа	II тип, слева	II тип, справа
0,95	500	500	500	500
0,9	200	200	100	100
0,8	100	130	40	40

Продолжение таблицы 5.11

0,7	50	70	20	30
0,6	30	60	20	20
0,5	20	50	20	20
0,4	20	40	20	20
0,3	20	20	20	20
0,2	20	20	20	20
0,1	20	20	20	20
0,05	20	20	20	20

Исследование распределений статистики Колмогорова по цензурированным выборкам при проверке сложных гипотез о согласии

Как уже отмечалось во введении и в разделе 1.5, в случае проверки сложных гипотез статистики непараметрических критериев теряют свойство «свободы от распределения», т.е. предельные распределения статистик становятся зависящими от вида проверяемой гипотезы, метода оценивания параметров, какие именно параметры оцениваются. В случае цензурированных выборок предельные распределения статистики Колмогорова, очевидно, зависят еще и от типа и степени цензурирования.

На рис. 5.6 приведено распределение статистики Колмогорова  при проверке гипотезы о согласии, когда по выборке вычислялись ОМП параметров масштаба и формы распределения Вейбулла в случае цензурирования I типа справа, степень цензурирования , потенциальный объем выборки . На этом же рисунке также приведено распределение Колмогорова , которому подчиняется статистика , если по выборке не оцениваются параметры.

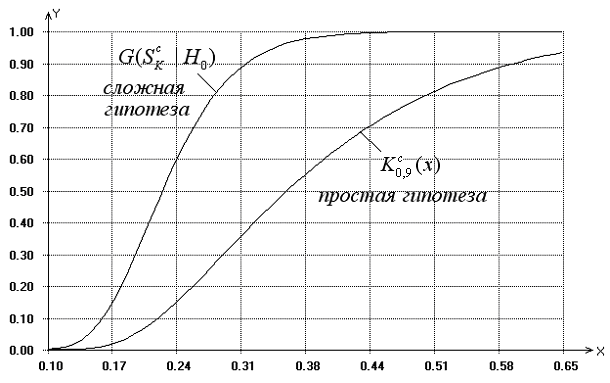
Рис. 5.6. Распределения статистики Колмогорова при проверке

простой и сложной гипотез по цензурированной выборке

Результаты моделирования однозначно указывают на то, что предельные распределения статистики  при условии оценивания параметров конкретного закона настолько сильно отличаются от распределения Колмогорова, что использование последнего в случае проверки сложной гипотезы никак не может быть оправдано из-за высокого риска неверных выводов.

Наиболее реальный выход видится в моделировании предельных законов распределения статистик непараметрических критериев и в последующей идентификации полученных эмпирических законов. Под идентификацией понимается выбор такого теоретического закона распределения, который наиболее хорошо согласуется с эмпирической функцией распределения. Результаты такого моделирования позволяют, с одной стороны, количественно оценить возможные ошибки в случае пренебрежения фактом оценивания по выборке параметров наблюдаемого закона, с другой стороны, дают возможность с достаточной для практики точностью использовать эти результаты при проверке гипотез.

Результаты исследования методами статистического моделирования распределений статистики Колмогорова, полученных с использованием ОМП параметров проверяемых распределений, при различной величине степени цензурирования  показывают, что при  начиная с  и при  – с , с дальнейшим увеличением объема выборки между распределениями статистики значимых различий уже не наблюдается. Это, по существу, указывает на то, что эти распределения (при ) соответствуют некоторому (неизвестному) предельному распределению статистики Колмогорова. Значит, если смоделировать эмпирическое распределение статистики Колмогорова при  для заданного закона распределения , соответствующего проверяемой гипотезе, заданной величины  и структуры цензурирования, а затем осуществить идентификацию этого эмпирического закона, то мы получим аппроксимацию предельного закона распределения статистики Колмогорова.

Реализованный алгоритм численного моделирования выглядит следующим образом.

1. Моделируется  выборок заданного объема  в соответствии с заданным законом распределения .

2. По каждой выборке оцениваются параметры этого закона распределения (один параметр, или другой, или два одновременно).

3. Вычисляются значения соответствующих непараметрических статистик.

4. По накопленной выборке значений статистики объема  анализируется полученное эмпирическое распределение статистики и осуществляется его идентификация.

Как показывают результаты идентификации, распределения статистики Колмогорова при проверке сложных гипотез с использованием ОМП по цензурированным выборкам хорошо описываются логарифмически нормальным законом (lnN).

Результаты моделирования представлены в табл. 5.12 – 5.15.

Таблица 5.12

Предельные распределения статистики Колмогорова в случае проверки сложной гипотезы о согласии с экспоненциальным законом и оценивании параметра масштаба методом максимального правдоподобия

	I тип, слева	I тип, справа	II тип, слева	II тип, справа
0,95	lnN(-1,7696, 0,2799)	lnN(-1,7035, 0,3122)	lnN(-1,7512, 0,2578)	lnN(-1,6717, 0,2861)
0,9	lnN (-1,4189, 0,2659)	lnN(-1,3542, 0,2983)	lnN(-1,4159, 0,2604)	lnN(-1,3393, 0,2854)
0,8	lnN (-1,0583, 0,2681)	lnN(-1,0177, 0,2873)	lnN(-1,0580, 0,2661)	lnN(-1,0114, 0,2812)
0,7	lnN (-0,8395, 0,2742)	lnN(-0,8293, 0,2815)	lnN(-0,8375, 0,2726)	lnN(-0,8260, 0,2789)
0,6	lnN (-0,6830, 0,2785)	lnN(-0,6982, 0,2773)	lnN(-0,6836, 0,2781)	lnN(-0,6961, 0,2749)
0,5	lnN (-0,5671, 0,2848)	lnN(-0,6009, 0,2718)	lnN(-0,5678, 0,2846)	lnN(-0,6006, 0,2704)
0,4	lnN (-0,4781, 0,2844)	lnN(-0,5197, 0,2666)	lnN(-0,4780, 0,2838)	lnN(-0,5191, 0,2666)
0,3	lnN (-0,4147, 0,2761)	lnN(-0,4654, 0,2644)	lnN(-0,4174, 0,2761)	lnN(-0,4641, 0,2631)
0,2	lnN (-0,3739, 0,2666)	lnN(-0,4117, 0,2585)	lnN(-0,3723, 0,2690)	lnN(-0,4126, 0,2590)
0,1	lnN (-0,3501, 0,2586)	lnN(-0,3770, 0,2567)	lnN(-0,3536, 0,2595)	lnN(-0,3779, 0,2567)
0,05	lnN (-0,3452, 0,2546)	lnN(-0,3591, 0,2581)	lnN(-0,3466, 0,2585)	lnN(-0,3594, 0,2581)

Таблица 5.13

Предельные распределения статистики Колмогорова для случая проверки сложной гипотезы о согласии с распределением Рэлея и оценивании параметра масштаба методом максимального правдоподобия

	I тип, слева	I тип, справа	II тип, слева	II тип, справа
0,95	lnN(-1,7748, 0,2803)	lnN(-1,7010, 0,3110)	lnN(-1,7516, 0,2574)	lnN(-1,6709, 0,2866)
0,9	lnN(-1,4195, 0,2668)	lnN(-1,3563, 0,2960)	lnN(-1,4115, 0,2596)	lnN(-1,3417, 0,2860)
0,8	lnN(-1,0557, 0,2675)	lnN(-1,0213, 0,2889)	lnN(-1,0561, 0,2656)	lnN(-1,0149, 0,2823)
0,7	lnN(-0,8391, 0,2750)	lnN(-0,8283, 0,2821)	lnN(-0,8390, 0,2750)	lnN(-0,8226, 0,2792)
0,6	lnN(-0,6846, 0,2772)	lnN(-0,6963, 0,2775)	lnN(-0,6846, 0,2768)	lnN(-0,6941, 0,2749)
0,5	lnN(-0,5669, 0,2826)	lnN(-0,5986, 0,2741)	lnN(-0,5672, 0,2821)	lnN(-0,5973, 0,2721)
0,4	lnN(-0,4780, 0,2832)	lnN(-0,5241, 0,2664)	lnN(-0,4790, 0,28300	lnN(-0,5230, 0,2654)
0,3	lnN(-0,4163, 0,2772)	lnN(-0,4646, 0,2647)	lnN(-0,4161, 0,27570	lnN(-0,4637, 0,2639)
0,2	lnN(-0,3688, 0,2670)	lnN(-0,4132, 0,2607)	lnN(-0,3697, 0,2665)	lnN(-0,4131, 0,2604)
0,1	lnN(-0,3508, 0,2595)	lnN(-0,3765, 0,2582)	lnN(-0,3515, 0,2594)	lnN(-0,3769, 0,2579)
0,05	lnN(-0,3473, 0,2592)	lnN(-0,3609, 0,2589)	lnN(-0,3475, 0,2594)	lnN(-0,3610, 0,2590)

Таблица 5.14

Предельные распределения статистики Колмогорова для случая проверки сложной гипотезы о согласии с распределением Вейбулла и оценивании двух параметров (масштаба и формы) методом максимального правдоподобия

	I тип, слева	I тип, справа	II тип, слева	II тип, справа
0,95	lnN(-1,8407, 0,2813)	lnN(-1,8519, 0,2766)	lnN(-1,8161, 0,2493)	lnN(-1,8315, 0,2480)
0,9	lnN(-1,4942, 0,2674)	lnN(-1,5105, 0,2619)	lnN(-1,4822, 0,2495)	lnN(-1,5021, 0,2486)
0,8	lnN(-1,1547, 0,2589)	lnN(-1,1734, 0,2571)	lnN(-1,1480, 0,2497)	lnN(-1,1682, 0,2487)
0,7	lnN(-0,9631, 0,2519)	lnN(-0,9777, 0,2504)	lnN(-0,9605, 0,2463)	lnN(-0,9752, 0,2463)
0,6	lnN(-0,8314, 0,2472)	lnN(-0,8419, 0,2458)	lnN(-0,8293, 0,2445)	lnN(-0,8415, 0,2435)
0,5	lnN(-0,7322, 0,2408)	lnN(-0,7431, 0,2415)	lnN(-0,7288, 0,2400)	lnN(-0,7412, 0,2395)
0,4	lnN(-0,6517, 0,2386)	lnN(-0,6635, 0,2404)	lnN(-0,6517, 0,2397)	lnN(-0,6613, 0,2392)
0,3	lnN(-0,5961, 0,2333)	lnN(-0,6038, 0,2349)	lnN(-0,5940, 0,2340)	lnN(-0,6050, 0,2349)
0,2	lnN(-0,5439, 0,2307)	lnN(-0,5550, 0,2303)	lnN(-0,5461, 0,2303)	lnN(-0,5552, 0,2297)
0,1	lnN(-0,5105, 0,2267)	lnN(-0,5163, 0,2274)	lnN(-0,5092, 0,2249)	lnN(-0,5142, 0,2249)
0,05	lnN(-0,5004, 0,2255)	lnN(-0,5019, 0,2253)	lnN(-0,4951, 0,2266)	lnN(-0,5021, 0,2261)

Таблица 5.15

Предельные распределения статистики Колмогорова для случая проверки сложной гипотезы о согласии с логарифмически (ln) нормальным  или нормальным распределениями и оценивании двух параметров (сдвига и масштаба) методом максимального правдоподобия

	Логарифмически (ln) нормальное распределение		Нормальное распределение
	I тип	II тип	I тип	II тип
0,95	lnN(-1,8490, 0,2797)	lnN(-1,8275, 0,2467)	lnN(-1,8499, 0,2785)	lnN(-1,8275, 0,2467)
0,9	lnN(-1,5031, 0,2664)	lnN(-1,4899, 0,2497)	lnN(-1,5013, 0,2665)	lnN(-1,4902, 0,2498)
0,8	lnN(-1,1589, 0,2570)	lnN(-1,1572, 0,2502)	lnN(-1,1592, 0,2588)	lnN(-1,1547, 0,2527)
0,7	lnN(-0,9646, 0,2550)	lnN(-0,9626, 0,2488)	lnN(-0,9659, 0,2511)	lnN(-0,9659, 0,2474)
0,6	lnN(-0,8322, 0,2472)	lnN(-0,8329, 0,2467)	lnN(-0,8336, 0,2491)	lnN(-0,8302, 0,2478)
0,5	lnN(-0,7322, 0,2449)	lnN(-0,7284, 0,2436)	lnN(-0,7309, 0,2450)	lnN(-0,7291, 0,2425)
0,4	lnN(-0,6545, 0,2406)	lnN(-0,6536, 0,2405)	lnN(-0,6527, 0,2414)	lnN(-0,6505, 0,2425)
0,3	lnN(-0,5901, 0,2395)	lnN(-0,5925, 0,2351)	lnN(-0,5929, 0,2379)	lnN(-0,5915, 0,2355)
0,2	lnN(-0,5430, 0,2358)	lnN(-0,5446, 0,2328)	lnN(-0,5414, 0,2346)	lnN(-0,5384, 0,2325)
0,1	lnN(-0,5044, 0,2309)	lnN(-0,5029, 0,2297)	lnN(-0,5046, 0,2298)	lnN(-0,5032, 0,2290)
0,05	lnN(-0,4891, 0,2289)	lnN(-0,4894, 0,2272)	lnN(-0,4911, 0,2285)	lnN(-0,4910, 0,2285)

Исследуем влияние применения поправок на смещение ОМП по сильно цензурированным выборкам, полученных в главе 4 диссертации, на распределения статистики Колмогорова при проверке сложных гипотез.

В [99, 100] нами было исследовано влияние точности оценивания на распределения статистик непараметрических критериев Колмогорова, Смирнова, ,  Мизеса в случае проверки сложных гипотез по полным выборкам. Показано, что незначительные отклонения в распределениях оценок практически не влияют на распределения непараметрических статистик. При наличии же значимых различий между распределениями «точных» и приближенных оценок различия между распределениями статистик, полученных при использовании тех и других оценок становятся весьма существенными. Выявленная закономерность распространяется и на случай использования ОМП и ОМП с поправкой на смещение.

Поправки на смещение ОМП получены для объемов выборки , для больших  величина смещения близка к нулю. Очевидно, что асимптотические свойства ОМП и ОМП с поправкой на смещение совпадают, следовательно, предельные распределения непараметрических статистик с использованием этих оценок также совпадают. Однако на практике, естественно, имеют дело с выборками ограниченного объема и, как правило, . В такой ситуации различия между ОМП и ОМП с поправкой на смещение при высокой степени цензурирования существенны и, следовательно, различия между распределениями статистики Колмогорова при использовании тех и других оценок также существенны. Например, на рис. 5.7 представлены распределения статистики Колмогорова при проверке сложной гипотезы о согласии с распределением Вейбулла по цензурированным слева выборкам II типа объема  и использовании ОМП с поправкой на смещение.  – это соответствующая аппроксимация предельного распределения статистики Колмогорова при вычислении ОМП параметров распределения Вейбулла (см. табл. 5.14),  – предельное распределение статистики Колмогорова при проверке простой гипотезы.

Рис. 5.7. Распределения статистики Колмогорова по цензурированным слева выборкам II типа

Таким образом, применение поправок на смещение ОМП по цензурированным выборкам оказывает существенное влияние на распределения статистики Колмогорова при проверке сложных гипотез. Значит пользоваться полученными аппроксимациями предельных распределений статистики Колмогорова при использовании ОМП с поправками на смещение ,  нельзя. Т.е. поправку на смещение нужно делать после проверки гипотезы о согласии полученной выборки наблюдений с предполагаемым законом распределения.