x1 Ј x2 Ј … Ј xn.
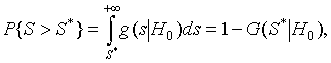
где
G(S|H0) – распределение статистики критерия при справедливости гипотезы H0.Сложная проверяемая гипотеза имеет вид
H0: F(x)О{F(x,q), qОQ}, где F(x,q) – функция распределения вероятностей, с которой проверяется согласие наблюдаемой выборки, Q – множество возможных значений параметра q (скалярного или векторного).При проверке сложных гипотез, когда по той же самой выборке оцениваются параметры наблюдаемого закона распределения вероятностей, непараметрические критерии согласия типа Колмогорова, Смирнова,
w2 и W2 Мизеса теряют свойство “свободы от распределения”. В этом случае предельные распределения статистик этих критериев будут зависеть от закона, которому подчинена наблюдаемая выборка. Более того, распределения статистик G(S|H0) непараметрических критериев согласия зависят от целого ряда факторов, определяющих “сложность” гипотезы. На распределение G(S|H0) влияют: вид наблюдаемого закона распределения F(x,q), соответствующего истинной гипотезе H0; тип оцениваемого параметра и количество оцениваемых параметров; в некоторых ситуациях конкретное значение параметра (например, в случае гамма-распределения); используемый метод оценивания параметров.При проверке согласия опытного распределения с теоретическим распределением случайной величины X действуют в соответствии с пп. 1-7.
x1 Ј x2 Ј … Ј xn.
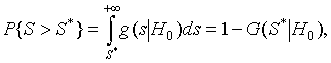
где
G(S|H0) – распределение статистики критерия при справедливости гипотезы H0.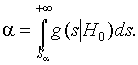
Гипотеза о согласии отвергается, если значение статистики попадает в критическую область, т. е. при
S* > Sa .