1.1. Контрольные карты для управления процессом по уровню настройки
1.2. 
-карты для средних значений
1.6. Контрольные карты для управления процессом по технологическому рассеянию
1.7. 
-карты стандартных
отклонений
2. Модифицированные карты Шухарта для количественных признаков
2.1. Коэффициенты устойчивости производственного процесса
2.2. Определение контрольных границ
3. Контрольные карты с памятью
3.1. Введение в контрольные карты с памятью..
3.2. KUSUM-карты средних значений
3.3. Метод обработки KUSUM-карт с использованием V-маски
3.4. Метод обработки KUSUM-карт с использованием схемы интервалов принятия решений
3.5. EWMA-карты средних значений
Таблица 2.
Квантили 
распределения
размаха
1. Контрольные карты Шухарта
Контрольные карты качества служат для постоянного контроля за тем, чтобы процесс оставался статистически подконтрольным.
Для контроля по качественному признаку используют: 
-карты
для подсчета числа дефектов на единицу товарной продукции; 
-карты для
подсчета числа дефектов на условную единицу. В обоих случаях исходным
распределением является распределение Пуассона, если допустить, что
последовательность дефектов имеет пуассоновский процесс. (Распределение
Пуассона часто аппроксимируют нормальным законом.)
Число дефектных изделий в выборке можно применить непосредственно в качестве
контрольной величины или разделить ее на объем выборки и получить долю
дефектных изделий. В первом случае работают с -картами, во втором – с 
-картами.
В обоих случаях исходным будет биномиальное распределение, так как
выборка берется из текущего процесса производства и поэтому генеральная
совокупность бесконечна. (Биномиальное распределение также часто аппроксимируют
нормальным.)
Для контроля по количественным признакам используют контрольные карты, как правило, опирающиеся на нормальное распределение. Поэтому следует удостовериться в правильности этого предположения относительно наблюдаемого признака на основании применения критериев согласия. В противном случае применение как критерия Бартлетта, так и аппарата контрольных карт может оказаться некорректным.
Используются следующие виды контрольных карт
качества: для средних значений – -карты; для медиан – 
-карты;
для текущих (исходных) значений – -карты (карты экстремальных
значений); для стандартных отклонений – -карты; для размахов – 
-карты.
1.1. Контрольные карты для управления процессом по уровню настройки
Уровень 
средней линии для всех контрольных
карт для уровня настройки определяется некоторым требуемым значением 
(заданное,
опытное значение или оценка, полученная на начальном этапе невозмущенного
процесса). Определение верхних и нижних контрольных границ (OEG и
UEG) верхних и нижних предупредительных границ (OWG и
UWG) зависит от информации о рассеянии процесса 
,
которая может быть задана в виде заданного или опытного значения или в виде
оценки 
. Границы для контрольных карт
находятся в виде:
,
(1)
,
(2)
где
коэффициенты 
и 
, как правило,
определяются таким образом, чтобы контрольная величина при невозмущенном
процессе могла оказаться вне интервалов (UEG, OEG)
или (UWG, OWG) с вероятностями 
или 
соответственно.
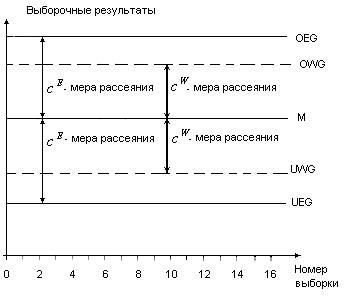
Рис. 1. Схема двусторонней контрольной карты для управления по уровню настройки
Коэффициенты и зависят от объема
выборки и контрольной величины.
При построении карт предполагается, что контролируемый
признак 
распределен по нормальному закону
с параметрами (
, 
).
1.2. 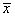-карты
для средних значений
Контрольной величиной является выборочное среднее арифметическое
.
Если рассеяние процесса постоянно, то эта величина
подчиняется нормальному закону с параметрами (, /
).
Двусторонний доверительный интервал для 
определяется
уравнением
,
где
–
соответствующий квантиль стандартного нормального закона, определяемый
соотношением
.
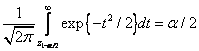Контрольные границы принимают значения
,
(3)
предупредительные границы –
.
(4)
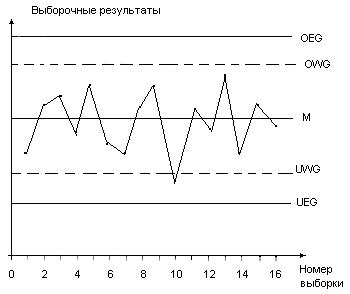
Рис. 2. Двусторонняя контрольная карта средних значений
1.3. 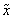-карты
медиан
В качестве контрольной величины рассматривается медиана по
выборке объема
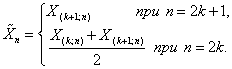
Контрольная величина 
распределена с
математическим ожиданием 
и дисперсией 
.
Двусторонний доверительный интервал для определяется
уравнением
,
где
-
табулирован.
Контрольные границы принимают значения
,
(5)
предупредительные границы –
. (6)
1.4. 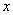-карты
исходных значений
Контрольной величиной для
карты исходных значений является сам выборочный вектор 
. В контрольную
карту вносят все его значения. Если только все значения наблюдений лежат внутри
контрольных или предупредительных границ, то остановки процесса на подналадку
или появления сигнала предупреждения не происходит. Необходимость коррекции
связана с минимальным и максимальным элементами выборки. Поэтому карту
исходных значений называют еще картой экстремальных значений.
Все компонентов выборки независимы
и распределены по нормальному закону с параметрами (, ).
Контрольные границы определяются таким образом,, чтобы все
компоненты 
при невозмущенном процессе (при 
)
лежали внутри границ с вероятностью 
. Поскольку все независимы и
одинаково распределены, то это условие можно сформулировать по другому:
контрольные границы определяются так, чтобы любой компонент находился
внутри этих границ с вероятностью 
.
Поэтому двусторонний доверительный интервал для определяется
уравнением
,
где
–
квантиль стандартного нормального закона при 
.
Контрольные границы принимают значения
,
(7)
предупредительные границы –
.
(8)
Из рассмотренных контрольных карт наибольшей мощностью обладают карты средних значений, наименьшей – карты исходных значений.
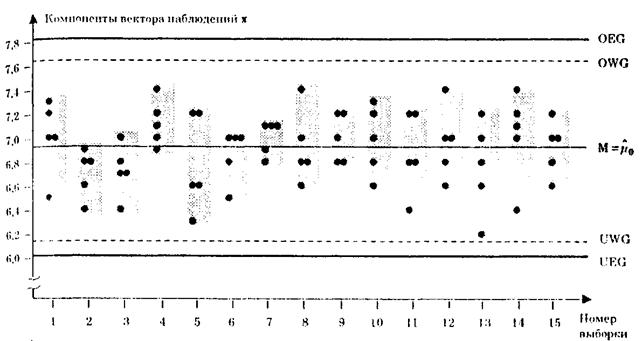
Рис. 3. Карта исходных значений с двусторонними границами
1.5. Карты отдельных значений
Применяются, если измерение
признака качества связано с большими затратами или если по сравнению со
скоростью протекания процесса измерение происходит очень медленно. Контрольной
величиной в данном случае является результат измерения 
выборки объемом
из
текущего производства. Переменные подчиняются нормальному закону с
параметрами (, ). Поэтому при нормальном
ходе процесса (при ) выполняется условие
.
Контрольные границы принимают значения
,
(9)
предупредительные границы –
.
(10)
1.6. Контрольные карты для управления процессом по технологическому рассеянию
Для управления процессом по технологическому рассеянию, как правило, применяют односторонние контрольные карты. Этому случаю соответствует проверка гипотезы
: 
,
(11)
против
: 
.
(12)
В более редких ситуациях строят двусторонние карты, которым соответствует проверка гипотез
: 
,
(13)
против
: 
.
(14)
Уровень средней линии у всех контрольных карт для
управления процессом по технологическому рассеянию определяется известной
информацией о требуемом значении (заданное или опытное значение или
оценка) 
. Контрольные и предупредительные
границы принимают вид:
,
(15)
,
(16)
где
коэффициенты и , как правило,
определяют таким образом, чтобы контрольная величина при невозмущенном процессе
достигала или превышала соответствующие границы OEG или OWG с
вероятностями или соответственно.
При построении карт предполагается, что контролируемый
признак распределен по нормальному закону
с параметрами (, ).
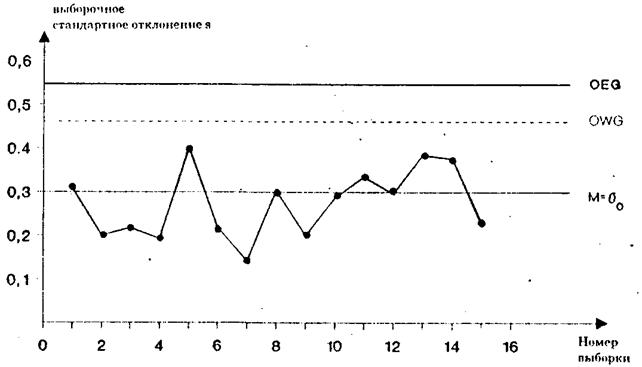
Рис. 4. Карта стандартных отклонений с односторонними границами и выборочными данными, полученными в фазе пуска процесса
1.7. 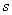-карты
стандартных отклонений
Контрольной величиной для карт стандартных отклонений является выборочное стандартное отклонение
.
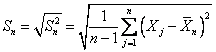Поскольку принадлежит нормальному закону с
параметрами (, ), то величина 
имеет 
-распределение.
При нормальном ходе процесса, то есть при 
, справедливо соотношение
.
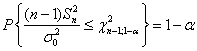(17)
Для 
отсюда следует, что
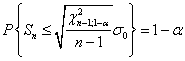. (18)
Откуда контрольная и предупредительная границы имеют вид:
,
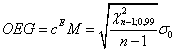(19)
.
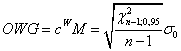(20)
1.8. 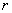-карты
размахов
Контрольной величиной для карты размахов является размах (разность между наибольшим и наименьшим значением)
(21)
выборки
объемом с признаком качества ,
имеющим нормальный закон с параметрами (, ),. Если квантиль порядка
функции
распределения 
обозначить через , а
квантиль распределения нормированного размаха выборки 
через 
, то по
определению квантилей должно выполняться равенство
.
Для невозмущенного процесса, то есть и тем самым 
,
выполняется условие
.
(22)
Следовательно, контрольные и предупредительные границы равны соответственно
,
(23)
.
(24)
Квантили 
и 
табулированы (Таблица 2).
2. Модифицированные карты Шухарта для количественных признаков
2.1. Коэффициенты устойчивости производственного процесса
Модифицированные карты Шухарта предназначены для управления процессом по уровню настройки с учетом заданных полей допусков.
Если заданы поля допуска 
и 
для признака
качества , то на этапе пуска
производственного процесса необходимо оценить его устойчивость. Степень
устойчивости процесса зависит от того, насколько велика доля изделий, для
которых признак качества находится в поле допуска [,]. На
практике об устойчивости процесса судят по коэффициенту устойчивости – безразмерной
величине, служащей мерой устойчивости производственного процесса.
Наиболее распространенной мерой устойчивости процесса является неотрицательный коэффициент
.
(25)
Например, требование 
требует выполнения
условия 
. Коэффициент 
не зависит от
уровня настройки процесса. Его можно интерпретировать как меру потенциальной
устойчивости процесса.
Коэффициент
,
(26)
где
(27)
и
(28)
–
середина поля допуска, учитывает не только рассеяние, но и уровень настройки
процесса. Он характеризует различие между действительным и оптимальным уровнем
настройки процесса 
. Чем меньше 
, тем ближе
уровень настройки к оптимальному. Если 
коэффициент 
лежит между 0 и
.
Следующий коэффициент устойчивости
, (29)
где
.
Поэтому для коэффициента 
можно использовать
выражение
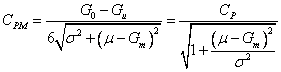. (30)
В то же время
.
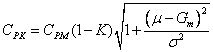(31)
2.2. Определение контрольных границ
Пусть заданы два предельных значения и .
Уровень средней линии определяется серединой поля
допуска . Взятое из текущего процесса
изделие с показателем качества бракуется как дефектное с
вероятностью
. (32)
В случае нормального закона показателя качества –
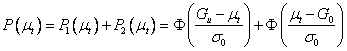. (33)
Минимальная доля брака согласно (85) получается при 
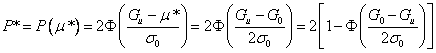. (34)
При определении контрольных границ на контрольной
карте для управления процессом по уровню настройки с учетом заданных границ
поля допуска [,] исходят из того, что
уровень настройки процесса внутри поля
допуска может смещаться от его середины до уровня, при котором доля брака 
достигает
некоторого критического значения 
. При достижении критического
значения процесс останавливают на
поднастройку с заданной вероятностью 
. То есть, для используемой
контрольной статистики
. (35)
При нормальности закона распределения рассматриваемой
статистики 
показателя качества процесса при
вычислении контрольных границ можно полагать, что
, (36)
.
(37)
При значениях коэффициента
, (38)
. (39)
И с хорошим приближением можно считать
,
(40)
.
(41)
При этом 
и 
вычисляются как:
,
(42)
.
(43)
Так как контрольные границы по (92)-(93) должны лежать
внутри интервала [,] и в связи с
симметричностью одинаково удалены от и , их можно представить в
виде:
, (44)
.
(45)
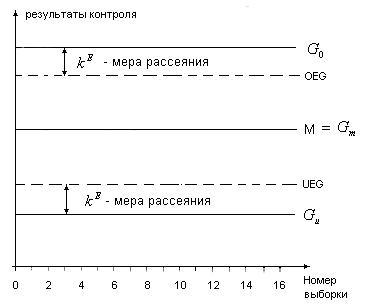
Рис.5. Схема двусторонней карты для управления процессом по уровню настройки
2.3. Карты средних значений
Так как контрольная величина
.
подчиняется
нормальному закону с параметрами (, /), по
соотношениям (40)–(41) можно получить выражение для определения контрольных
границ:
,
.
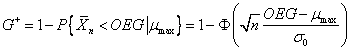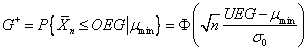Отсюда следует, что
,
.
Разрешая эти выражения относительно контрольных границ, получаем:
,
(46)
.
(47)
Подставляя сюда (94)-(95), определим контрольные границы:
,
(48)
(49)
при
. (50)
2. 4. Карты медиан
В качестве контрольной величины используется выборочная медиана
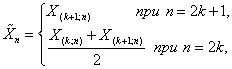
подчиняющаяся
нормальному закону с математическим ожиданием и дисперсией .
Аналогично предыдущему случаю, контрольные границы получаются в виде:
, (51)
,
(52)
но при
.
(53)
2.5. Карты исходных значений
Контрольные границы вычисляются таким образом, чтобы
все компоненты выборки объемом с заданной вероятностью лежали
внутри этих границ, если доля брака достигает заданного критического значения .
Контрольные границы находятся как:
,
(54)
,
(55)
где
,
(56)
.
(57)
3. Контрольные карты с памятью
3.1. Введение в контрольные карты с памятью
При использовании контрольных карт Шухарта решение о переналадке производственного процесса принимается на основании анализа текущей выборки. Карты Шухарта называются еще контрольными картами без памяти. При выборочном контроле в контрольных картах с памятью принимаются во внимание результаты контроля предыдущих выборок. Такие контрольные карты могут быть более чувствительными к возмущениям, то есть уже при самом начале сдвига уровня настройки или изменения технологического рассеяния указывать на необходимость вмешательства в процесс.
В картах Шухарта в качестве контрольной величины
используется некоторая статистика (функция) 
от текущей выборки 
, в
качестве которой могут быть, например, выборочное среднее или выборочное
стандартное отклонение. В контрольных картах с памятью наряду с результатами
текущего контроля учитываются результаты контроля на предыдущих выборках. Если
контрольная величина учитывает результаты контроля во всех предыдущих выборках,
то соответствующая контрольная карта обладает неограниченной памятью. Если
используются результаты контроля только по последним 
выборкам, то
карта имеет конечную память. При 
– карты без памяти.
Различают карты с равномерной и неравномерной
памятью. В первом случае величины из разных этапов контроля в контрольной
величине имеют одинаковый вес, во втором – различный. В картах второго типа
значимость результатов контроля, как правило, уменьшается с удалением от
настоящего момента времени 
: карты с убывающей памятью.
Для различения выборочных характеристик из разных
выборок вводится индекс времени 
, принимающий значения от 1 до : 
–
момент взятия первой выборки, 
– последней. Все взятые до момента
времени выборки образуют систему
выборочных векторов
, 
.
Для каждого выборочного вектора по единому правилу
строится статистика 
. Система выборочных характеристик 
, 
, …, 
преобразуется
в скалярную контрольную величину 
. Наиболее простой является
линейная комбинация
.
(58)
Вид
памяти зависит от коэффициентов 
в (110).
В картах Шухарта:
, (59)
,
(60)
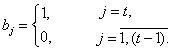(61)
В MOSUM-картах:
,
(62)
,
(63)
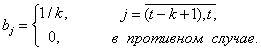(64)
Контрольной величиной является скользящее среднее 
последних
выборок (mosum= moving sum). Карты имеют конечную и
равномерную память за периодов.
В EWMA-картах используют контрольную величину
, 
,
(65)
причем
задается
как требуемое значение уровня настройки процесса или технологического рассеяния.
Контрольная величина является экспоненциально взвешенным средним значением (EWMA=exponential weighted moving average)
всех выборочных характеристик, полученных к моменту времени . При
последовательной подстановке получаем:
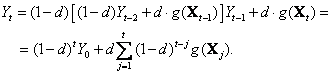(66)
Таким образом,
,
(67)
, .
(68)
Эти карты имеют неограниченную неравномерную память.
В KUSUM-картах используется контрольная величина:
,
(69)
причем
задается
как требуемое значение уровня настройки процесса или технологического
рассеяния.
Таким образом,
,
(70)
, .
(71)
Контрольную величину (69) можно интерпретировать как
накопленную сумму отклонений всех выборочных характеристик от заданного
значения . KUSUM-карты
имеют равномерную память, которая начинается с момента времени 
.
3.2. KUSUM-карты средних значений
Пусть контролю подлежит среднее значение распределенного
по нормальному закону с параметрами (, ) признаками качества с
постоянной технологической дисперсией . Пусть для задано значение
и
недопустимы слишком сильные отклонения от него в обе стороны.
В карте средних значений Шухарта контрольная
величина 
, представляющая собой среднее
значение выборки объемом , взятой к моменту ,
подчиняется (согласно принятому условию) нормальному распределению с
параметрами (, /), поэтому 
.
Отсюда следует, что 
, если 
. Значения
контрольной величины карты средних значений Шухарта при постоянном уровне
настройки процесса 
рассеяны относительно прямой 
,
параллельной оси времени . При нормальном ходе процесса,
когда 
, график реализаций величины 
колеблется
вокруг прямой 
.
При использовании KUSUM-карт
средних значений отклонения 
между -м выборочным значением и
заданным значением суммируются с начала процесса или
с момента последней поднастройки
.
(72)
В силу того, что величина 
должна
подчиняться нормальному закону с параметрами (
, /),
статистика имеет математическое ожидание
.
(73)
Следовательно,
,
если . (74)
Это означает, что математическое ожидание
накопленной суммы отклонений 
при постоянном уровне настройки
процесса являются линейной функцией от .
Соответствующая прямая имеет крутизну 
. При график значений (кривая)
случайно блуждает относительно оси времени . Если, начиная с момента
времени 
, происходит смещение уровня
настройки 
, то кривая с момента времени 
начнет
колебаться относительно полупрямой, начинающейся при и имеющей
крутизну подъема .
Таким образом, если кривая на карте начинает слишком быстро падать или возрастать, то это означает, что произошло недопустимое смещение уровня настройки, и следует предпринять вмешательство в ход процесса.
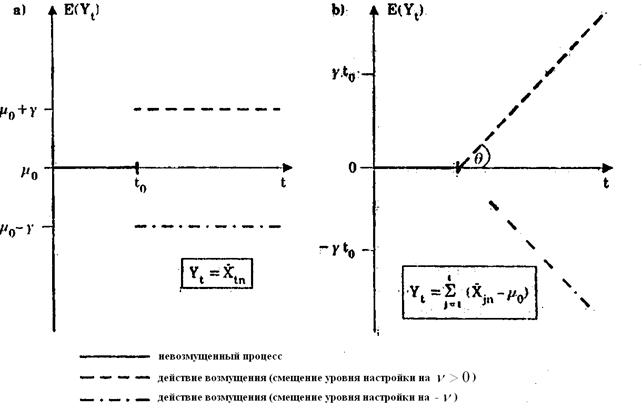
Рис. 6. Математическое ожидание контрольной величины карты средних значений Шухарта и KUSUM-карты как функции времени
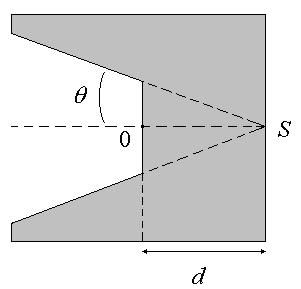
3.3. Метод обработки KUSUM-карт с использованием V-маски
V-маской называется шаблон с
разрезом в виде буквы V, форма которой определяется
углом раскрытия 2
и высотой основания 
(см.
рис.).
V-маску помещают так, чтобы последнее значение KUSUM-значение на контрольной карте совпало с точкой 0.
Если весь график [последовательность значений точек
(1, 
),
(2, 
),
…, (,) на
карте] находится внутри V-маски (внутри угла), то можно
сделать вывод о том, что до момента времени смещение уровня
настройки процесса от требуемого значения было незначительным и
вмешиваться в процесс с целью подналадки не следует.
Если график пересекает одну из сторон V-маски (сторону угла), то это свидетельствует о том, что
отклонение хода процесса от номинала к моменту времени , (
)
настолько велико, что необходимо предпринять вмешательство в процесс,
увеличивая или уменьшая значение уровня настройки в зависимости от того, какая
из сторон маски пересекается графиком.
При заданных вероятностях ошибок первого 
и
второго рода 
параметры V-маски
определяются соотношениями
,
(75)
где 
, 
. Если
пренебречь , то получается хорошее приближение
.
(76)
Угол 2, определяющий раскрытие V-маски, находится из соотношения 
:
.
(77)
Это справедливо, если величины по оси абсцисс и оси
ординат откладываются в тех же единицах. Если 
единиц (>0)
по оси ординат соответствует одной единице по оси абсцисс, то угол определяется
по более общей формуле:
.
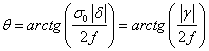(78)
3.4. Метод обработки KUSUM-карт с использованием схемы интервалов принятия решений
В этом случае вводится две новые KUSUM-величины:
,
(79)
,
(80)
где – некоторая
постоянная. Реализации величин (131)-(132) 
и 
сравниваются с
границами интервала принятия решений [
, 
].
При работе с такой контрольной картой действуют следующим образом:
1. Пока
выполняются условия 
и 
, контрольная карта не
заполняется.
2. Начиная
с 
подсчитывается
сумма . Эта сумма уменьшается или
увеличивается в зависимости от величины ее новых слагаемых. Если она становится
меньшей или равной нулю, процесс счета прекращается.
3. Начиная
с 
подсчитывается
сумма . Эта сумма уменьшается или
увеличивается в зависимости от величины ее новых слагаемых. Если она становится
большей или равной нулю, процесс счета прекращается.
4. После
прекращения счета образование возобновляется, как только
выполнится , возобновление подсчета начинается,
как только выполнится .
5. Если
достигает
значения или превышает его, то это
свидетельствует о том, что отклонение хода процесса от номинала к
моменту времени , (
) настолько велико, что
необходимо предпринять вмешательство в процесс, уменьшая уровень настройки.
6. Если
достигает
значения или опускается ниже его, то это
свидетельствует о том, что отклонение хода процесса от номинала к
моменту времени , () настолько велико, что
необходимо предпринять вмешательство в процесс, увеличивая уровень настройки.
Средняя линия такой контрольной карты 
,
контрольные границы – горизонтальные линии на расстоянии от средней.
При заданных вероятностях ошибок первого и
второго рода параметры определяется
соотношением
,
(81)
что справедливо, если
величины по оси абсцисс и оси ординат откладываются в тех же единицах. Если единиц
(>0)
по оси ординат соответствует одной единице по оси абсцисс, то
.
(82)
Для контрольных границ
.
(83)
3.5. EWMA-карты средних значений
Они обладают такой же высокой чувствительностью по отношению к малым смещениям уровня настройки, как и KUSUM-карты.
Пусть контролю подлежит среднее значение распределенного
по нормальному закону с параметрами (, ) признаками качества с
постоянной технологической дисперсией . Требуемое значение уровня
настройки равно .
Контрольная величина определяется рекурсивным соотношением
, ,
(84)
где 
- среднее
значение в -й выборке, имеющей распределение
нормальное распределение с параметрами (,/).
Если начальное значение 
, то
,
(85)
Выбором параметра
контрольной карты определяется степень влияния
результатов, полученных при анализе предыдущих выборок, на принятие решения по
результатам контроля текущей выборки. Чем больше , тем меньше влияние
предыстории изменения качества. При =1, получаем контрольную карту
Шухарта без памяти. Чем ближе значение к 0, тем больше веса приближаются
к весовым коэффициентам KUSUM-карт.
Контрольные границы OEG и UEG определяются соотношениями:
,
(86)
. (87)
С учетом того, что
выборочные средние значения независимы и подчиняются нормальному распределению
с параметрами (,/), дисперсия
переменной (85) составляет
.
(88)
Асимптотическая дисперсия
при 
.
(89)
,
(92)
.
(91)
При определении
параметров карты задается значение 
, а величины и определяются
по номограммам.