6. Задачи корреляционного анализа
Выделение аномальных измерений
Выделение аномальных измерений
6.7. Частная линейная регрессия
6.10. Статистические распределения
При анализе совокупности случайных величин нас может интересовать либо взаимозависимость между несколькими случайными величинами, либо зависимость одной или большего числа величин от остальных.
Теория корреляции занимается изучением взаимозависимости. Именно на это нацелены алгоритмы и методы корреляционного анализа многомерных случайных величин. С помощью аппарата корреляционного анализа можно убедиться в наличии взаимозависимости величин, исследовать взаимозависимость величин при устранении влияния совокупности других (частная корреляция), рассмотреть зависимость одной величины от группы величин (множественная корреляция), прийти к выводу о наличии статистической зависимости, возможно даже предположить и наличие функциональной зависимости, скрытой за ошибками результатов измерений. Но с помощью статистических методов невозможно установить причинной связи. Исследование функциональных закономерностей, присущих соответствующей области, лежит вообще за рамками статистики. Корреляционный анализ не занимается и построением регрессионных зависимостей. Исследованием статистических зависимостей, построением моделей занимаются уже в рамках регрессионного анализа.
С использованием результатов корреляционного анализа исследователь может делать определённые выводы о наличии и характере взаимозависимости, что уже само по себе может представлять существенную информацию об исследуемом объекте. Результаты могут подсказать и направление дальнейших исследований, и совокупность требуемых методов, в том числе статистических, необходимых для более полного изучения объекта.
Особенно реальную пользу применение аппарата корреляционного анализа может принести на стадии ранних исследований в областях, где характеры причин определённых явлений ещё недостаточно понятны. Это может касаться изучения очень сложных систем различного характера: как технических, так и социальных.
Комплекс программ корреляционного анализа предназначен для анализа и обработки выборок многомерных случайных величин (векторного параметра некоторой системы или некоторого технологического процесса).
Он позволяет вычислять оценки вектора математических ожиданий, ковариационной матрицы, матрицы парных корреляций, матрицы корреляционных отношений, матриц частных корреляций, вектора множественных корреляций, проверять гипотезы о значимости различных параметров или о равенстве их определенным значениям, о наличии функциональных зависимостей.
Предоставляет возможности анализа многомерных выборок на наличие аномальных измерений, на случайность, на принадлежность к нормальной генеральной совокупности.
Позволяет вычислять вероятности и квантили для ряда статистических распределений, наиболее часто используемых в задачах проверки статистических гипотез.
Использование комплекса дает возможность выявления характера статистических зависимостей между компонентами многомерной случайной величины и определения меры линейности этих связей.
Комплекс программ будет весьма полезен при обработке результатов экспериментальных исследований и анализе статистических данных в технике, медицине, биологии, при обработке социологических обследований.
В состав программного обеспечения входят 5 файлов:
kora.exe
kora00.exe
kora01.exe
kr_ega.exe
title.leo
kora.hlp
act.txt
Головной программой является kora.exe. Остальные файлы должны находиться в этой же директории.
Файлы kora00.exe и kora01.exe осуществляют вычисления в соответствии с алгоритмами выбранных задач и запускаются непосредственно программой kora.exe. Управляющая информация о заданной задаче, исходной выборке, ее местонахождении и, определенные пользователем известные ему параметры задачи передаются через формируемый файл с именем KoraBase.txt.
В процессе работы по желанию пользователя система создает файл результатов (по умолчанию KoraRes.txt).
В меню системы входит ряд сервисных функций, поддерживающих выбор требуемой задачи, определение входного файла, содержащего данные с исходной выборкой, задание размерности анализируемой случайной величины и объема выборки, задание имени файла, в который будут записаны результаты вычислений, запуск выбранной задачи на выполнение. Встроенный редактор позволяет создавать исходные файлы с данными, просматривать и при необходимости корректировать файлы с результатами.
Движение по разделам меню и выбор определенной задачи или функции осуществляется перемещением указателя курсора и клавишей <Enter> или с помощью манипулятора "мышь". Выбор определенной задачи осуществляется повторным нажатием клавиши <Enter>. Для возврата на предыдущий уровень меню необходимо нажать клавишу <Esc>.
Для обращения за пояснениями к выбираемой задаче или функции (для обращения за справками к файлу kora.hlp) необходимо нажать клавишу <F1>. Выбор соответствующей подсказки может быть осуществлен указателем курсора и клавишей <Enter> или манипулятором "мышь". Отказ от помощи - манипулятором "мышь", а при ее отсутствии - клавишей <Esc>.
Файл act.txt - это демонстрационный
файл с исходной выборкой случайной величины размерности ![]() и объемом
и объемом ![]() является
примером подготовки исходных данных. Все приводимые ниже примеры используют в
качестве исходной выборки этот файл.
является
примером подготовки исходных данных. Все приводимые ниже примеры используют в
качестве исходной выборки этот файл.
Информация, содержащаяся в этом файле, имеет следующий вид:
|
X1 |
X2 |
X3 |
X4 |
|
154.0 |
178.0 |
59.0 |
21.0 |
|
133.0 |
164.0 |
63.0 |
27.0 |
|
58.0 |
75.0 |
36.0 |
18.0 |
|
145.0 |
161.0 |
62.0 |
10.0 |
|
94.0 |
107.0 |
48.0 |
26.0 |
|
... |
... |
... |
... |
|
85.0 |
91.0 |
48.0 |
25.0 |
Первая строка файла является символьной, она обязательно должна присутствовать, но может иметь и другой содержательный смысл (вид).
Результаты наблюдений многомерной случайной величины (выборка) должны быть представлены в исходном файле в аналогичном виде. размерность наблюдаемой величины определит количество X-столбцов, а объем выборки - количество строк.
|
№ |
X1 |
X2 |
X3 |
X4 |
№ |
X1 |
X2 |
X3 |
X4 |
|
1 |
154 |
178 |
59 |
21 |
31 |
98 |
140 |
40 |
30 |
|
2 |
133 |
164 |
63 |
27 |
32 |
97 |
115 |
86 |
35 |
|
3 |
58 |
75 |
36 |
18 |
33 |
105 |
101 |
55 |
15 |
|
4 |
145 |
161 |
62 |
10 |
34 |
71 |
93 |
43 |
7 |
|
5 |
94 |
107 |
48 |
26 |
35 |
39 |
69 |
30 |
29 |
|
6 |
113 |
141 |
64 |
20 |
36 |
122 |
147 |
55 |
28 |
|
7 |
86 |
97 |
44 |
23 |
37 |
33 |
52 |
25 |
38 |
|
8 |
121 |
127 |
57 |
33 |
38 |
78 |
117 |
56 |
11 |
|
9 |
119 |
138 |
62 |
19 |
39 |
114 |
138 |
62 |
15 |
|
10 |
112 |
125 |
51 |
27 |
40 |
125 |
149 |
63 |
20 |
|
11 |
85 |
97 |
45 |
25 |
41 |
73 |
76 |
32 |
21 |
|
12 |
41 |
72 |
45 |
5 |
42 |
77 |
85 |
43 |
24 |
|
13 |
96 |
113 |
51 |
16 |
43 |
47 |
61 |
36 |
16 |
|
14 |
45 |
89 |
41 |
13 |
44 |
68 |
85 |
38 |
15 |
|
15 |
99 |
109 |
49 |
29 |
45 |
137 |
142 |
61 |
21 |
|
16 |
51 |
95 |
46 |
33 |
46 |
44 |
69 |
32 |
27 |
|
17 |
101 |
114 |
63 |
9 |
47 |
92 |
116 |
48 |
7 |
|
18 |
169 |
209 |
73 |
19 |
48 |
141 |
157 |
54 |
30 |
|
19 |
87 |
101 |
55 |
21 |
49 |
155 |
193 |
60 |
29 |
|
20 |
88 |
139 |
65 |
30 |
50 |
136 |
155 |
65 |
6 |
|
21 |
83 |
98 |
46 |
25 |
51 |
82 |
81 |
41 |
17 |
|
22 |
106 |
111 |
58 |
25 |
52 |
136 |
163 |
55 |
27 |
|
23 |
92 |
104 |
45 |
20 |
53 |
72 |
79 |
43 |
23 |
|
24 |
85 |
103 |
46 |
21 |
54 |
66 |
81 |
40 |
21 |
|
25 |
112 |
118 |
55 |
33 |
55 |
42 |
61 |
29 |
22 |
|
26 |
98 |
102 |
48 |
14 |
56 |
113 |
123 |
49 |
6 |
|
27 |
103 |
108 |
50 |
20 |
57 |
42 |
85 |
36 |
22 |
|
28 |
99 |
119 |
60 |
11 |
58 |
133 |
147 |
52 |
12 |
|
29 |
104 |
128 |
41 |
25 |
59 |
153 |
179 |
72 |
27 |
|
30 |
107 |
118 |
65 |
12 |
60 |
85 |
91 |
48 |
25 |
Результаты вычислений оценок параметров или проверки конкретных гипотез могут выводиться либо в файл на диске, либо на экран. Но в последнем случае их затруднительно фиксировать.
При выборе вывода результатов "В файл" система предлагает вывод в файл "KoraRes.txt" в текущей директории, но может быть указан любой другой файл. При решении каждой очередной задачи результаты решения предыдущей теряются, если только Вы не поменяете имя файла вывода.
После завершения очередной задачи, результаты ее решения могут быть вызваны для визуального просмотра. Для этого в меню "Выход" должно быть выбрано подменю "Просмотр", а затем команда "Просмотр результатов".
6. Задачи корреляционного анализа
6.1. Проверка предпосылок
Сюда входят проверка выборки на наличие грубых, аномальных измерений, проверка гипотез о случайности выборочных данных и принадлежности выборки нормальной генеральной совокупности. Статистические выводы осуществляются отдельно по каждой компоненте наблюдённой многомерной случайной величины
Выделение аномальных измерений. Резко выделяющиеся наблюдения, или выбросы, могут быть реакцией системы на некоторое резкое случайное воздействие, либо быть ошибками измерений. Выброс может оказаться также одним из экстремальных значений случайной величины. В первом случае выброс должен быть отброшен, а во втором - он несёт полезную информацию о системе.
Если выборка взята из нормальной
совокупности с известной дисперсией, то самый простой анализ её на наличие
аномальных измерений может быть проведен по правилу “трёх сигм”. Пусть ![]() выборка одномерной
случайной величины,
выборка одномерной
случайной величины, ![]() - выборочное среднее. Тогда величины
- выборочное среднее. Тогда величины ![]() ,
распределены по нормальному закону с нулевым математическим ожиданием и
дисперсией
,
распределены по нормальному закону с нулевым математическим ожиданием и
дисперсией ![]() .
Поэтому как аномальные надо отбросить те наблюдения, для которых
.
Поэтому как аномальные надо отбросить те наблюдения, для которых ![]() .
.
Проверка случайности выборки. Внешним проявлением случайности наблюдений является полная непредсказуемость очередного результата. Наиболее часто при проверке случайности используется непараметрический критерий ранговой корреляции Кендалла.
Рангом ![]() i-го наблюдения
i-го наблюдения ![]() из выборки
из выборки ![]() называется
номер этого наблюдения в упорядоченной по возрастанию последовательности. Инверсией
называется ситуация, когда больший ранг предшествует меньшему:
называется
номер этого наблюдения в упорядоченной по возрастанию последовательности. Инверсией
называется ситуация, когда больший ранг предшествует меньшему: ![]() при
при ![]() .
.
Статистика
![]() ,
,
где ![]() - число инверсий в перестановке рангов,
- число инверсий в перестановке рангов, ![]() - объем
выборки, имеет нормальное распределение с нулевым математическим ожиданием и
дисперсией
- объем
выборки, имеет нормальное распределение с нулевым математическим ожиданием и
дисперсией 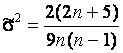 .
Гипотеза о случайности принимается, если
.
Гипотеза о случайности принимается, если ![]() и
и ![]() определяется из условия
определяется из условия
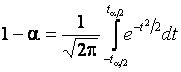 .
.
Проверка нормальности выборки. При проверке гипотезы о нормальности выборки одним из критериев проверки является следующий. Вычисляется статистика
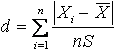 ,
,
где ![]() ,
, 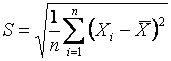 , которая при
, которая при ![]() распределена приближенно по
нормальному закону с математическим ожиданием
распределена приближенно по
нормальному закону с математическим ожиданием 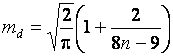 и дисперсией
и дисперсией 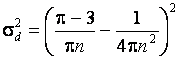 . Если
выполняется неравенство
. Если
выполняется неравенство
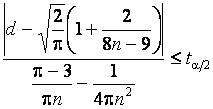 ,
,
где ![]() определяется как и в
предыдущем случае при проверке случайности, то гипотеза о нормальности
принимается.
определяется как и в
предыдущем случае при проверке случайности, то гипотеза о нормальности
принимается.
Примечание: При выявлении аномальных измерений, последние фиксируются в файле результатов, но не исключаются из входного файла. Поэтому следует помнить, что для того, чтобы эти измерения в дальнейшем не влияли на результаты анализа, Вы должны сами удалить указанные аномальные наблюдения из входного файла.
Ниже приведен результат решения этих задач с исходными данными из прилагаемого файла act.txt:
Файл ввода act.txt
В исходной выборке аномальных наблюдений нет
"Анализ выборки на случайность"
Уровень значимости alfa = 0.0500
Гипотеза о случайности выборки ПРИНИМАЕТСЯ
"Анализ выборки на нормальность"
Уровень значимости alfa = 0.0500
Гипотеза о нормальности выборки ПРИНИМАЕТСЯ
Известно, что задачи и методы корреляционного анализа опираются на многомерное нормальное распределение. И, очевидно, что если гипотеза о нормальности наблюденной выборки не отвергается, и выборка случайна, то дальнейшие выводы статистического анализа будут наиболее достоверными.
В то же время решение задач корреляционого анализа принесет несомненную пользу и в том случае, когда гипотеза о нормальности исходной выборки отвергается.
В данном случае могут решаться 2 задачи.
Первая - оценка параметров многомерного нормального распределения: вектора
математических ожиданий ![]() , где
, где ![]() -
- ![]() -мерная случайная величина,
ковариационной матрицы
-мерная случайная величина,
ковариационной матрицы ![]() и матрицы коэффициентов парных
корреляций с элементами
и матрицы коэффициентов парных
корреляций с элементами
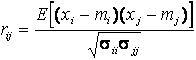 ,
,
где ![]() - математическое ожидание, а
- математическое ожидание, а ![]() -
диагональный элемент матрицы
-
диагональный элемент матрицы ![]() , дисперсия случайной компоненты
, дисперсия случайной компоненты ![]() .
.
Оценка максимального правдоподобия (ОМП)
математического ожидания многомерной случайной величины ![]() вычисляется по формуле
вычисляется по формуле
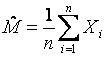 ,
,
где ![]() - выборка
- выборка ![]() -мерной случайной величины
-мерной случайной величины ![]() объёмом №.
Несмещенная ОМП ковариационной матрицы
объёмом №.
Несмещенная ОМП ковариационной матрицы ![]() определяется соотношением
определяется соотношением
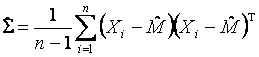 .
.
Элементы матрицы парных коэффициентов корреляции оцениваются в соответствии с выражением
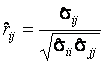 ,
,
где ![]() - элементы матрицы
- элементы матрицы ![]() .
.
Результаты оценивания параметров по выборке, содержащейся в файле act.txt, имеют вид:
Файл ввода act.txt
Вектор математического ожидания
|
№ |
1 |
2 |
3 |
4 |
|
1 |
9.603333e+01 |
1.151667e+02 |
5.070000e+01 |
2.093333e+01 |
Ковариационная матрица
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.0911510e+03 |
1.063689e+03 |
3.008068e+02 |
-2.218081e+00 |
|
2 |
1.063689e+03 |
1.185294e+03 |
3.135423e+02 |
7.231637e+00 |
|
3 |
3.008068e+02 |
3.135423e+02 |
1.423831e+02 |
-4.986442e+00 |
|
4 |
-2.218081e+00 |
7.231637e+00 |
-4.986442e+00 |
6.3351410e+01 |
Матрица парных коэффициентов корреляции
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
9.353179e-01 |
7.631606e-01 |
-8.436385e-03 |
|
2 |
9.353179e-01 |
1.000000e+00 |
7.632276e-01 |
2.639037e-02 |
|
3 |
7.631606e-01 |
7.632276e-01 |
1.000000e+00 |
-5.250291e-02 |
|
4 |
-8.436385e-03 |
2.639037e-02 |
-5.250291e-02 |
1.000000e+00 |
Этот же пункт меню предусматривает
проверку гипотез о равенстве математического ожидания некоторому известному
вектору, т.е. проверку гипотез вида ![]() .
.
Такая задача очень часто возникает на практике, когда, например, на основании наблюдений некоторого многомерного показателя технологического процесса желают убедиться, что эти показатели равны номинальному значению, т.е. процесс протекает нормально, а отклонения наблюденных значений от номинальных объясняются лишь ошибками наблюдений (измерений).
При решении этой задачи возможны две
ситуации: ковариационная матрица ![]() может быть известна из ранее проводимых
экспериментов, по другим выборкам, (в этом случае пользователь в процессе диалога
должен будет ввести элементы этой матрицы), или неизвестна, тогда в процессе
вычислений она должна быть оценена.
может быть известна из ранее проводимых
экспериментов, по другим выборкам, (в этом случае пользователь в процессе диалога
должен будет ввести элементы этой матрицы), или неизвестна, тогда в процессе
вычислений она должна быть оценена.
В случае проверки гипотезы ![]() при
известной ковариационной матрице вычисляется статистика
при
известной ковариационной матрице вычисляется статистика
![]() .
.
При справедливой гипотезе ![]() эта статистика имеет
эта статистика имеет ![]() распределение
с m степенями свободы. Таким образом, гипотеза
распределение
с m степенями свободы. Таким образом, гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где ![]() - уровень значимости и
- уровень значимости и
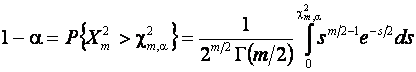 .
.
В случае проверки гипотезы ![]() при неизвестной
ковариационной матрице вычисляемая статистика имеет вид
при неизвестной
ковариационной матрице вычисляемая статистика имеет вид
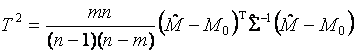 .
.
Если гипотеза ![]() справедлива, то эта статистика
подчиняется
справедлива, то эта статистика
подчиняется ![]() -распределению
Фишера с m и
-распределению
Фишера с m и ![]() степенями свободы. В данном случае
гипотеза
степенями свободы. В данном случае
гипотеза ![]() принимается,
если выполняется условие
принимается,
если выполняется условие
![]() .
.
Величина ![]() определяется из равенства
определяется из равенства
 ,
,
где ![]() .
.
В случае неизвестной матрицы по данным из файла act.txt имеем следующий результат:
Файл ввода act.txt
С уровнем значимости alfa = 0.0500 ОТВЕРГАЕТСЯ
гипотеза: МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ равно:
|
№ |
1 |
2 |
3 |
4 |
|
1 |
9.500000e+01 |
1.000000e+02 |
3.500000e+01 |
1.500000e+01 |
Этот пункт меню может выполняться либо с проверкой предпосылок, т.е. анализом на наличие грубых ошибок измерений, на случайность и нормальность, либо без. Если задание выполняется с проверкой предпосылок, и в выборке обнаруживаются аномальные измерения, то в дальнейшем анализе они не участвуют (но в исходном файле сохраняются!).
При выполнении этого задания вычисляются
оценки математического ожидания, ковариационной матрицы, матрицы парных корреляций,
проверяются гипотезы о значимости элементов этой матрицы, для значимых парных
корреляций строятся доверительные интервалы. Далее вычисляются оценки
корреляционных отношений и проверяются гипотезы о их значимости, т.е. гипотезы
вида ![]() :
: ![]() . Затем вычисляется
оценка матрицы частных корреляций, элементы которой представляют собой
корреляцию между соответствующими элементами, при условии что все остальные
. Затем вычисляется
оценка матрицы частных корреляций, элементы которой представляют собой
корреляцию между соответствующими элементами, при условии что все остальные ![]() компоненты
компоненты ![]() -мерной
случайной величины фиксированы (т.е. рассматривается условное распределение 2
компонент). Все элементы этой матрицы проверяются на значимость, для значимых
частных коэффициентов корреляции строятся доверительные интервалы.
-мерной
случайной величины фиксированы (т.е. рассматривается условное распределение 2
компонент). Все элементы этой матрицы проверяются на значимость, для значимых
частных коэффициентов корреляции строятся доверительные интервалы.
Вычисляется вектор множественных
коэффициентов корреляции, каждый элемент которого представляет собой корреляцию
(меру линейной зависимости) между соответствующей компонентой случайной
величины и множеством остальных ![]() компонент. Относительно каждого
элемента этого вектора проверяется гипотеза о значимости.
компонент. Относительно каждого
элемента этого вектора проверяется гипотеза о значимости.
Результаты выполнения этого пункта меню без проверки предпосылок для рассматриваемого примера имеют вид:
Файл ввода act.txt
Вектор математического ожидания
|
№ |
1 |
2 |
3 |
4 |
|
1 |
9.603333e+01 |
1.151667e+02 |
5.070000e+01 |
2.093333e+01 |
Ковариационная матрица
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.0911510e+03 |
1.063689e+03 |
3.008068e+02 |
-2.218081e+00 |
|
2 |
1.063689e+03 |
1.185294e+03 |
3.135423e+02 |
7.231637e+00 |
|
3 |
3.008068e+02 |
3.135423e+02 |
1.423831e+02 |
-4.986442e+00 |
|
4 |
-2.218081e+00 |
7.231637e+00 |
-4.986442e+00 |
6.3351410e+01 |
Матрица парных коэффициентов корреляции
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
9.353179e-01 |
7.631606e-01 |
-8.436385e-03 |
|
2 |
9.353179e-01 |
1.000000e+00 |
7.632276e-01 |
2.639037e-02 |
|
3 |
7.631606e-01 |
7.632276e-01 |
1.000000e+00 |
-5.250291e-02 |
|
4 |
-8.436385e-03 |
2.639037e-02 |
-5.250291e-02 |
1.000000e+00 |
Матрица значимых коэффициентов корреляции
Уровень значимости alfa = 0.0500
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
9.353179e-01 |
7.631606e-01 |
0.000000e+00 |
|
2 |
9.353179e-01 |
1.000000e+00 |
7.632276e-01 |
0.000000e+00 |
|
3 |
7.631606e-01 |
7.632276e-01 |
1.000000e+00 |
0.000000e+00 |
|
4 |
0.000000e+00 |
0.000000e+00 |
0.000000e+00 |
1.000000e+00 |
Доверительные интервалы для значимых парных коэф-в корреляции
Уровень значимости alfa =0.0500
|
Коэффициент корреляции |
Доверительный интервал |
|
r( 1, 2) = 0.9353179 |
0.8936307 0.9610038 |
|
r( 1, 3) = 0.7631606 |
0.6316382 0.8519835 |
|
r( 2, 3) = 0.7632276 |
0.6317346 0.8520275 |
Матрица корреляционных отношений
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
8.884497e-01 |
7.039601e-01 |
2.831308e-01 |
|
2 |
9.007756e-01 |
1.000000e+00 |
7.056496e-01 |
3.454498e-01 |
|
3 |
6.026155e-01 |
6.750155e-01 |
1.000000e+00 |
3.260075e-01 |
|
4 |
8.177995e-02 |
7.801921e-02 |
1.972346e-01 |
1.000000e+00 |
Матрица значимых корреляционных отношений
Уровень значимости alfa = 0.0500
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
8.884497e-01 |
7.039601e-01 |
0.000000e+00 |
|
2 |
9.007756e-01 |
1.000000e+00 |
7.056496e-01 |
3.454498e-01 |
|
3 |
6.026155e-01 |
6.750155e-01 |
1.000000e+00 |
3.260075e-01 |
|
4 |
0.000000e+00 |
0.000000e+00 |
0.000000e+00 |
1.000000e+00 |
Mатрица значимых корней кв. из корреляционных отношений
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
9.425761e-01 |
8.390233e-01 |
0.000000e+00 |
|
2 |
9.490920e-01 |
1.000000e+00 |
8.400295e-01 |
5.877498e-01 |
|
3 |
7.762831e-01 |
8.215933e-01 |
1.000000e+00 |
5.709707e-01 |
|
4 |
0.000000e+00 |
0.000000e+00 |
0.000000e+00 |
1.000000e+00 |
Матрица частных коэффициентов корреляции
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
8.455458e-01 |
2.073441e-01 |
-7.151330e-02 |
|
2 |
8.455458e-01 |
1.000000e+00 |
2.247293e-01 |
1.153210e-01 |
|
3 |
2.073441e-01 |
2.247293e-01 |
1.000000e+00 |
-9.491602e-02 |
|
4 |
-7.151330e-02 |
1.153210e-01 |
-9.491602e-02 |
1.000000e+00 |
Матрица значимых частных коэффициентов корреляции
Уровень значимости alfa = 0.0500
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
8.455458e-01 |
0.000000e+00 |
0.000000e+00 |
|
2 |
8.455458e-01 |
1.000000e+00 |
0.000000e+00 |
0.000000e+00 |
|
3 |
0.000000e+00 |
0.000000e+00 |
1.000000e+00 |
0.000000e+00 |
|
4 |
0.000000e+00 |
0.000000e+00 |
0.000000e+00 |
1.000000e+00 |
Доверительные интервалы для
Значимых частных коэффициентов корреляции
Уровень значимости alfa = 0.0500
|
Коэффициент корреляции |
Доверительный интервал |
|
r( 1, 2) =0.8455458 |
0.7513443 0.9059756 |
Вектор множественных коэффициентов корреляции
|
№ |
1 |
2 |
3 |
4 |
|
1 |
9.387504e-01 |
9.392858e-01 |
7.781507e-01 |
1.355840e-01 |
Вектор значимых множественных коэффициентов корреляции
Уровень значимости alfa = 0.0500
|
№ |
1 |
2 |
3 |
4 |
|
1 |
9.387504e-01 |
9.392858e-01 |
7.781507e-01 |
0.000000e+00 |
В данном пункте может анализироваться либо
вся матрица парных корреляций (оценивание, проверка значимости и построение
доверительных интервалов для значимых), либо отдельный коэффициент парной
корреляции. В последнем случае можно раздельно или совместно решать следующие
задачи: определение оценки парного коэффициента корреляции, проверка гипотезы о
его значимости (гипотезы вида ![]() :
: ![]() ), проверка, при необходимости, гипотезы
вида
), проверка, при необходимости, гипотезы
вида ![]() :
: ![]() (т.е. равенства его
определенному конкретному значению), а также построение для него
доверительного интервала.
(т.е. равенства его
определенному конкретному значению), а также построение для него
доверительного интервала.
Если оценка ковариационной матрицы ![]() уже известна,
то оценка парного коэффициента корреляции может быть найдена в соответствии с
выражением
уже известна,
то оценка парного коэффициента корреляции может быть найдена в соответствии с
выражением
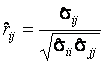 ,
,
где ![]() - элемент матрицы
- элемент матрицы ![]() .
.
При проверке гипотезы ![]() вычисляется статистика
вычисляется статистика
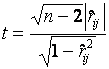 ,
,
которая при справедливой гипотезе ![]() имеет t-распределение
Стьюдента с
имеет t-распределение
Стьюдента с ![]() степенями
свободы. При конкурирующей гипотезе
степенями
свободы. При конкурирующей гипотезе ![]() гипотеза
гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где ![]() - уровень значимости. Величина
- уровень значимости. Величина ![]() при
при ![]() определяется
равенством
определяется
равенством
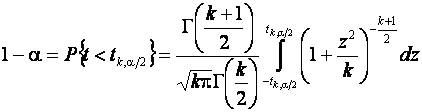 .
.
При проверке гипотезы ![]() статистика
статистика
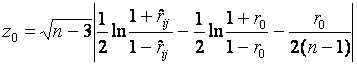 ,
,
при справедливой гипотезе ![]() подчиняется
стандартному нормальному распределению. Гипотеза
подчиняется
стандартному нормальному распределению. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где ![]() - квантиль стандартного нормального
распределения и
- квантиль стандартного нормального
распределения и
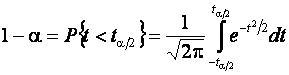 .
.
Доверительный интервал для парного коэффициента корреляции определяется неравенством
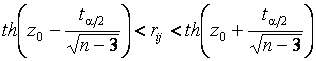 .
.
Ниже представлены результаты проверки
гипотезы о значимости, т.е. гипотезы вида ![]() , и гипотезы вида
, и гипотезы вида ![]() , для выборки
из файла act.txt:
, для выборки
из файла act.txt:
Файл ввода act.txt
Парный коэффициент корреляции r( 1, 2)=0.935318
ЗНАЧИМ с уровнем значимости alfa = 0.0500
Гипотеза: r=0.50000 ОТКЛОНЯЕТСЯ при alfa = 0.0500
Гипотеза будет принята при alfa < 2.93e-05
Доверительный интервал = (0.893631,0.961004)
Зачастую хотелось бы проверить гипотезу
вида ![]() :
:
![]() . А
сделать этого нельзя, так как в вычисляемой статистике оказывается 0 в
знаменателе. Но в то же время, Мы можем проверить, например, гипотезу вида
. А
сделать этого нельзя, так как в вычисляемой статистике оказывается 0 в
знаменателе. Но в то же время, Мы можем проверить, например, гипотезу вида ![]() :
: ![]() , т.е. сравнить с
величиной близкой к 1. Выдача результата в таком случае для нашей выборки имеет
вид:
, т.е. сравнить с
величиной близкой к 1. Выдача результата в таком случае для нашей выборки имеет
вид:
Файл ввода act.txt
Оценка парного коэф. корреляции r( 1, 2)=0.93532
Гипотеза: r=0.99000 ОТКЛОНЯЕТСЯ при alfa = 0.0500
Гипотеза будет принята при alfa < 5.36e-13
Корреляционное отношение случайной
величины ![]() по
по
![]() определяется
отношением дисперсии условного математического ожидания
определяется
отношением дисперсии условного математического ожидания ![]() к дисперсии
к дисперсии ![]() :
:
![]() .
.
Соотношение между коэффициентом корреляции
![]() и
корреляционным отношением
и
корреляционным отношением ![]() позволяет сделать следующие выводы:
позволяет сделать следующие выводы:
а) ![]() , если
, если ![]() и
и ![]() независимы;
независимы;
б) ![]() , тогда и только тогда, когда имеется
строгая линейная функциональная зависимость
, тогда и только тогда, когда имеется
строгая линейная функциональная зависимость ![]() от
от ![]() ;
;
в) ![]() , тогда и только тогда, когда имеется
строгая нелинейная функциональная зависимость
, тогда и только тогда, когда имеется
строгая нелинейная функциональная зависимость ![]() от
от ![]() ;
;
г) ![]() , тогда и только тогда, когда регрессия
, тогда и только тогда, когда регрессия ![]() по
по ![]() строго
линейна, но нет функциональной зависимости;
строго
линейна, но нет функциональной зависимости;
д) ![]() , указывает на то, что не существует
функциональной зависимости и некоторая нелинейная кривая регрессии "подходит"
лучше, чем "наилучшая" прямая линия.
, указывает на то, что не существует
функциональной зависимости и некоторая нелинейная кривая регрессии "подходит"
лучше, чем "наилучшая" прямая линия.
То есть, равенство квадрата коэффициента корреляции корреляционному отношению указывает на то, что для регрессии нельзя найти лучшей кривой, чем прямая линия.
Оценка корреляционного отношения определяется выражением
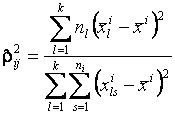 ,
,
где ![]() - количество интервалов значений
(сечений) для компоненты
- количество интервалов значений
(сечений) для компоненты ![]() ,
, ![]() - среднее значение
- среднее значение ![]() -го
-го ![]() -сечения,
-сечения, ![]() - число
наблюдений в этом сечении,
- число
наблюдений в этом сечении, ![]() - значение компоненты
- значение компоненты ![]() с номером
с номером ![]() в
в ![]() -м
-м ![]() -сечении,
-сечении, ![]() .
.
При проверке гипотезы ![]() используется
статистика
используется
статистика
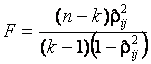 ,
,
которая при справедливой гипотезе ![]() имеет F-распределение
Фишера с числом степеней свободы
имеет F-распределение
Фишера с числом степеней свободы ![]() и
и ![]() . Гипотеза
. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где ![]() - критическая точка критерия с уровнем
значимости
- критическая точка критерия с уровнем
значимости ![]() .
.
При проверке гипотезы ![]() (гипотезы о линейности
регрессии
(гипотезы о линейности
регрессии ![]() по
по
![]() )
статистика имеет вид
)
статистика имеет вид
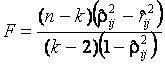 .
.
При справедливой гипотезе ![]() она подчиняется F-распределению
Фишера с числом степеней свободы
она подчиняется F-распределению
Фишера с числом степеней свободы ![]() и
и ![]() . Гипотеза
. Гипотеза ![]() принимается, если
принимается, если
![]() .
.
Данный пункт меню предусматривает либо
анализ матрицы корреляционных отношений (оценивание и проверку значимости
элементов матрицы), либо анализ определенного корреляционного отношения между
компонентами с номерами i и j случайной величины: вычисление
оценки ![]() ,
проверку значимости (гипотеза
,
проверку значимости (гипотеза ![]() :
: ![]() ), проверку линейности регрессии
), проверку линейности регрессии ![]() по
по ![]() (проверяется
гипотеза о равенстве корреляционного отношения квадрату парного коэффициента
корреляции).
(проверяется
гипотеза о равенстве корреляционного отношения квадрату парного коэффициента
корреляции).
Результат анализа выборки из файла act.txt в последнем случае имеет вид:
Файл ввода act.txt
Корреляционное отношение ro( 1, 2)=0.888450
ЗНАЧИМО с уровнем значимости alfa = 0.0500
Коэффициент корреляции r ( 1, 2)=0.935318
С уровнем значимости alfa = 0.0500
ПРИНИМАЕТСЯ гипотеза: ro=r*r
(наилучшая регрессия x( 1) по x( 2) - линейная) Гипотеза: ro=r*r будет отвергнута при alfa > 8.17e-01
В случае двух нормальных или почти нормальных случайных величин коэффициент корреляции между ними может быть использован в качестве меры взаимозависимости. На практике при интерпретации "взаимозависимости" приходится сталкиваться с трудностями следующего характера: если одна величина коррелирована с другой, то это может быть всего лишь отражением того факта, что они обе коррелированы с некоторой третьей величиной или совокупностью величин. Указанная возможность приводит к необходимости рассмотрения условных корреляций между двумя величинами при фиксированных значениях остальных величин, т.е. частных корреляций.
Если корреляция между двумя величинами уменьшается, когда мы фиксируем некоторую другую случайную величину (компоненту многомерной величины), то это означает, что их взаимозависимость возникает частично через воздействие этой величины; если же частная корреляция равна нулю или очень мала, то мы делаем вывод, что их взаимозависимость целиком обусловлена этим воздействием. Наоборот, когда частная корреляция больше первоначальной корреляции между двумя величинами, то мы заключаем, что другие величины ослабляли эту связь, или, можно сказать, "маскировали" корреляцию.
По существу, мы должны рассматривать условное
распределение ![]() подвектора
подвектора ![]() при известном подвекторе
при известном подвекторе ![]() и
анализировать корреляцию между компонентами подвектора
и
анализировать корреляцию между компонентами подвектора ![]() .
.
Представим случайный вектор ![]() в следующем
виде
в следующем
виде
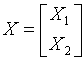 ,
,
где ![]() ,
, ![]() , соответственно, вектор математических
ожиданий и ковариационную матрицу
, соответственно, вектор математических
ожиданий и ковариационную матрицу
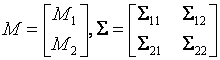 .
.
Если случайный вектор ![]() подчиняется
нормальному закону распределения с вектором средних
подчиняется
нормальному закону распределения с вектором средних ![]() и ковариационной
матрицей
и ковариационной
матрицей ![]() ,
то условное распределение подвектора
,
то условное распределение подвектора ![]() при известном
при известном ![]() является нормальным с
математическим ожиданием
является нормальным с
математическим ожиданием ![]() и ковариационной матрицей
и ковариационной матрицей ![]() , где
, где ![]() ,
, ![]() .
.
ОМП для частного коэффициента корреляции определяется следующим соотношением
 ,
,
где ![]() - элемент i-й строки и j-го
столбца матрицы
- элемент i-й строки и j-го
столбца матрицы ![]() . В данном случае при оценке
взаимозависимости между компонентами
. В данном случае при оценке
взаимозависимости между компонентами ![]() и
и ![]() случайной величины
случайной величины ![]() исключается влияние
компонент
исключается влияние
компонент ![]() .
.
При проверке гипотез вида ![]() и
и ![]() , а также
при построении доверительных интервалов для частного коэффициента корреляции
используются те же самые статистики, что и для парного коэффициента корреляции.
В этом случае в соответствующих соотношениях
, а также
при построении доверительных интервалов для частного коэффициента корреляции
используются те же самые статистики, что и для парного коэффициента корреляции.
В этом случае в соответствующих соотношениях ![]() заменяется на
заменяется на ![]() , где
, где ![]() - объём
выборки,
- объём
выборки, ![]() -
размерность случайного вектора,
-
размерность случайного вектора, ![]() - число компонент в условном
распределении (в частном случае
- число компонент в условном
распределении (в частном случае ![]() ).
).
В этом пункте меню может анализироваться
или вся матрица частных корреляций (оценивание, проверка значимости и
построение доверительных интервалов для значимых коэффициентов при условии, что
остальные ![]() компоненты
компоненты
![]() -мерной
величины фиксированы), или отдельный коэффициент частной корреляции. В
последнем случае можно, решая задачи отдельно или одновременно, найти оценку
частного коэффициента корреляции, проверить гипотезу о его значимости, при
необходимости проверить гипотезу вида
-мерной
величины фиксированы), или отдельный коэффициент частной корреляции. В
последнем случае можно, решая задачи отдельно или одновременно, найти оценку
частного коэффициента корреляции, проверить гипотезу о его значимости, при
необходимости проверить гипотезу вида ![]() , а также построить доверительный интервал
для частного коэффициента корреляции.
, а также построить доверительный интервал
для частного коэффициента корреляции.
Для выборки из файла act.txt результаты имеют следующий вид:
Файл ввода act.txt
Частный коэффициент корреляции r( 1, 2) = 0.845546
при фиксированных компонентах с индексами: 3, 4,
ЗНАЧИМ с уровнем значимости alfa = 0.0500
Гипотеза: частный коэф-т корреляции r( 1, 2)=0.700000 ОТВЕРГАЕТСЯ с уровнем значимости alfa = 0.0500
Гипотеза будет принята при alfa < 6.51e-03
Доверительный интервал =(0.751344,0.905976)
В предыдущих параграфах было получено, что
парный коэффициент корреляции ![]() , а вычисленный в данном пункте частный
коэффициент корреляции при исключении влияния на корреляцию компонент
, а вычисленный в данном пункте частный
коэффициент корреляции при исключении влияния на корреляцию компонент ![]() и
и ![]() равен
0.845546. Т.е. связь
равен
0.845546. Т.е. связь ![]() с
с ![]() частично осуществляется через
частично осуществляется через ![]() и
и ![]() . Продолжив
анализ и вычислив коэффициент корреляции при исключении влияния только
. Продолжив
анализ и вычислив коэффициент корреляции при исключении влияния только ![]() и только
и только ![]() , получим,
соответственно, 0.845086 и 0.935900. Отсюда можно сделать вывод, что связь
, получим,
соответственно, 0.845086 и 0.935900. Отсюда можно сделать вывод, что связь ![]() с
с ![]() осуществляется
частично через
осуществляется
частично через ![]() , но компонента
, но компонента ![]() на эту связь
практически не влияет. Кроме того, если в дальнейшем у Вас возникнет необходимость
в построении регрессионной модели, то, если рассматривать только регрессию
на эту связь
практически не влияет. Кроме того, если в дальнейшем у Вас возникнет необходимость
в построении регрессионной модели, то, если рассматривать только регрессию ![]() по
по ![]() , то наилучшая
модель линейная, а, если включать в нее
, то наилучшая
модель линейная, а, если включать в нее ![]() , то, возможно, нелинейная модель окажется
предпочтительней. Что касается компоненты
, то, возможно, нелинейная модель окажется
предпочтительней. Что касается компоненты ![]() , то ее влияние не значимо, и,
следовательно, присутствие в регрессионной модели будет излишним.
, то ее влияние не значимо, и,
следовательно, присутствие в регрессионной модели будет излишним.
6.7. Частная линейная регрессия
На основе частных коэффициентов корреляции можно найти оценки параметров частных линейных регрессионных зависимостей. Каждая i-я строка вычисляемой матрицы представляет собой линейную регрессионную модель вида
![]()
где в правой части равенства ![]() - элементы i-й
строки матрицы коэффициентов (
- элементы i-й
строки матрицы коэффициентов (![]() ),
), ![]() - условное математическое ожидание
случайной величины
- условное математическое ожидание
случайной величины ![]() .
.
Соответствующее уравнение регрессии имеет вид:
![]() .
.
Правомерность использования линейной регрессионной модели, описывающей связь между компонентами случайной величины выявляется в результате анализа соответствующих парных и частных коэффициентов корреляции и корреляционных отношений.
Для выборки из файла act.txt результаты имеют следующий вид:
Файл ввода act.txt
Матрица частных коэффициентов линейной регрессии
|
№ |
1 |
2 |
3 |
4 |
|
1 |
1.000000e+00 |
8.147302e-01 |
3.149224e-01 |
-1.032269e-01 |
|
2 |
8.775273e-01 |
1.000000e+00 |
3.542393e-01 |
1.727579e-01 |
|
3 |
1.365143e-01 |
1.425688e-01 |
1.000000e+00 |
-9.020554e-02 |
|
4 |
-4.954284e-02 |
7.698020e-02 |
-9.987264e-02 |
1.000000e+00 |
Т.е. линейная регрессия, например, для ![]() будет иметь
вид:
будет иметь
вид:
![]() .
.
Множественный коэффициент корреляции является мерой зависимости компоненты случайной величины от некоторого множества компонент.
Можно рассматривать корреляцию между одной компонентой случайного вектора и множеством всех остальных или каким-то подмножеством.
Следует отметить, что множественный
коэффициент корреляции ![]() случайной величины
случайной величины ![]() относительно некоторого
множества других случайных величин всегда не меньше, чем абсолютная величина
любого парного коэффициента корреляции
относительно некоторого
множества других случайных величин всегда не меньше, чем абсолютная величина
любого парного коэффициента корреляции ![]() с таким же первичным индексом. Более
того, множественный коэффициент корреляции никогда нельзя уменьшить путем расширения
множества величин, относительно которых измеряется зависимость
с таким же первичным индексом. Более
того, множественный коэффициент корреляции никогда нельзя уменьшить путем расширения
множества величин, относительно которых измеряется зависимость ![]() .
.
Если коэффициент корреляции между ![]() и множеством
всех остальных компонент многомерной случайной величины равен нулю (
и множеством
всех остальных компонент многомерной случайной величины равен нулю (![]() :
: ![]() ), то все коэффициенты
корреляции этой величины относительно любого подмножества также равны 0, т.е.
величина
), то все коэффициенты
корреляции этой величины относительно любого подмножества также равны 0, т.е.
величина ![]() полностью
некоррелирована со всеми остальными величинами.
полностью
некоррелирована со всеми остальными величинами.
С другой стороны, если ![]() относительно множества
всех остальных компонент равен единице (
относительно множества
всех остальных компонент равен единице (![]() :
: ![]() ), то по крайней мере один из
коэффициентов корреляции относительно некоторого подмножества компонент должен
быть равен 1.
), то по крайней мере один из
коэффициентов корреляции относительно некоторого подмножества компонент должен
быть равен 1.
Надо отметить, что коэффициент корреляции,
например, между ![]() и множеством всех остальных компонент
является обычным коэффициентом корреляции между
и множеством всех остальных компонент
является обычным коэффициентом корреляции между ![]() и условным математическим
ожиданием
и условным математическим
ожиданием ![]() .
.
Если представим случайный вектор ![]() в виде
в виде
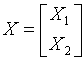 ,
,
где ![]() ,
, ![]() , и, соответственно, ковариационную
матрицу
, и, соответственно, ковариационную
матрицу
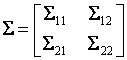 ,
,
тогда ОМП множественного коэффициента корреляции
между ![]() ,
,
![]() , и
множеством компонент
, и
множеством компонент ![]() определится соотношением
определится соотношением
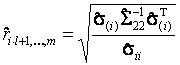 ,
,
где ![]() - элемент матрицы
- элемент матрицы ![]() , а
, а ![]() - i-я строка
матрицы
- i-я строка
матрицы ![]() .
.
При проверке гипотезы ![]() используется
статистика
используется
статистика
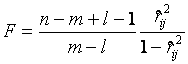 ,
,
которая при справедливой гипотезе ![]() имеет F-распределение
Фишера с числом степеней свободы
имеет F-распределение
Фишера с числом степеней свободы ![]() и
и ![]() . Гипотеза
. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где ![]() - уровень значимости, а
- уровень значимости, а ![]() - критическая
точка критерия с уровнем значимости
- критическая
точка критерия с уровнем значимости ![]() .
.
В данном пункте меню можно анализировать или вектор множественных коэффициентов корреляции (относительно множества всех остальных величин, образующих многомерную величину), находить оценки и проверять значимость компонент этого вектора, или анализировать множественный коэффициент корреляции между определенной компонентой и задаваемым подмножеством остальных компонент.
В последнем случае для выборки из файла act.txt получается результат:
Файл ввода act.txt
Множественный коэффициент корреляции между 1 компонентой
и множеством компонент с индексами: 3, 4,
r = 0.763818
ЗНАЧИМ с уровнем значимости alfa = 0.0500
Для сравнения, парный коэффициент
корреляции ![]() ,
а
,
а ![]() ,
и по абсолютной величине меньше вычисленного множественного коэффициента
корреляции.
,
и по абсолютной величине меньше вычисленного множественного коэффициента
корреляции.
Этот пункт предполагает решение задач проверки гипотез двух видов для каждой из компонент многомерной случайной величины:
·
проверку
гипотез о равенстве математических ожиданий компонент определенным значениям,
причем стандартные отклонения для этих компонент могут быть либо известны, либо
неизвестны (гипотезы ![]() :
: ![]() );
);
·
проверку
гипотез о равенстве стандартных отклонений известным величинам, и, в свою
очередь, соответствующие математические ожидания могут быть известны или нет
(гипотезы ![]() :
:
![]() ).
).
Следует подчеркнуть, что, строго говоря, проведение покомпонентного анализа оправдано при некоррелированности величин, входящих в систему.
Проверка гипотезы ![]() при известной
дисперсии компоненты
при известной
дисперсии компоненты ![]() . Вычисляемая статистика
. Вычисляемая статистика
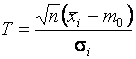 ,
,
где ![]() - среднее значение компоненты
- среднее значение компоненты ![]() , при
справедливой гипотезе
, при
справедливой гипотезе ![]() подчиняется стандартному нормальному
распределению. Гипотеза
подчиняется стандартному нормальному
распределению. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где критическое значение ![]() при заданном
при заданном ![]() определяется
равенством
определяется
равенством
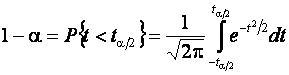 .
.
При проверке аналогичной гипотезы при неизвестной
дисперсии компоненты ![]() вычисляемая статистика
вычисляемая статистика
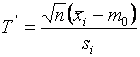 ,
,
где  и
и ![]() - j-е наблюдение компоненты
- j-е наблюдение компоненты ![]() , при
справедливой гипотезе
, при
справедливой гипотезе ![]() имеет t-распределение Стьюдента с
имеет t-распределение Стьюдента с
![]() степенью
свободы. Гипотеза
степенью
свободы. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где критическое значение ![]() при заданном
при заданном ![]() и
и ![]() определяется
равенством
определяется
равенством
 .
.
Проверка гипотезы ![]() при известном
математическом ожидании компоненты
при известном
математическом ожидании компоненты ![]() . В этом случае статистика
. В этом случае статистика
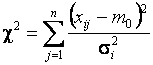
имеет ![]() -распределение с
-распределение с ![]() степенями свободы,
если гипотеза
степенями свободы,
если гипотеза ![]() справедлива. Гипотеза
справедлива. Гипотеза ![]() принимается, если
принимается, если
![]() ,
,
где значения ![]() и
и ![]() определяются равенством
определяются равенством
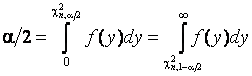 ,
,
и 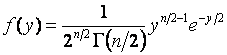 - функция плотности
- функция плотности ![]() -распределения с
-распределения с ![]() степенями
свободы.
степенями
свободы.
Если математическое ожидание компоненты неизвестно, то при проверке данной гипотезы вычисляемая статистика имеет вид
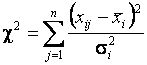
и при справедливой гипотезе ![]() имеет
имеет ![]() -распределение
с
-распределение
с ![]() степенями
свободы. Решение о принятии или отклонении гипотезы
степенями
свободы. Решение о принятии или отклонении гипотезы ![]() осуществляется как и в
предыдущем случае.
осуществляется как и в
предыдущем случае.
В случае проверки гипотез относительно математических ожиданий при неизвестных стандартных отклонениях для выборки из act.txt результаты имеют вид:
Файл ввода act.txt
"Покомпонентный анализ"
Проверка гипотезы о значимости отклонения математического ожидания от заданного значения при известном векторе стандартныx отклонений.
Уровень значимости alfa = 0.0500
|
№ компоненты |
Заданное значение мат.ожидания |
Вычисленное значение мат.ожидания |
Значимость отклонения |
|
1 |
9.600000e+01 |
9.603333e+01 |
Незначимо |
|
2 |
1.150000e+02 |
1.151667e+02 |
Незначимо |
|
3 |
5.000000e+01 |
5.070000e+01 |
Незначимо |
|
4 |
2.000000e+01 |
2.093333e+01 |
Незначимо |
6.10. Статистические распределения
В данном пункте меню предоставляется возможность вычисления вероятностей или квантилей для распределений наиболее часто используемых в задачах статистического анализа:
· стандартного нормального распределения;
·
![]() -распределения;
-распределения;
· t-распределения Стьюдента;
· F-распределения Фишера;
· B-распределения (бета).
Функция плотности нормального распределения имеет вид
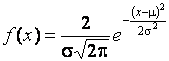 ,
,
![]() -распределения с числом степеней свободы
-распределения с числом степеней свободы ![]() -
-
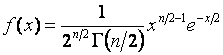 ,
,
t-распределения Стьюдента с числом степеней
свободы ![]() -
-
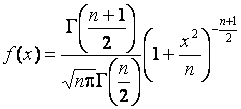
F-распределения Фишера с числом степеней свободы ![]() и
и ![]()
 ,
,
B-распределения -
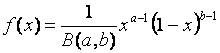 ,
,
где ![]() - бета-функция.
- бета-функция.
При определении вероятности того, что случайная величина X больше x вычисляется интеграл вида
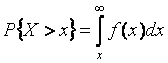 ,
,
а при вычислении квантили решается уравнение
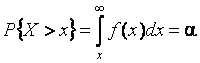 .
.
Например, при вычислении квантили для F-распределения Фишера с числом степеней свободы 3 и 8 результат имеет вид:
F-распределение Фишера (числа ст.св.- 3,8)
P{ X ≥2.92380e+00} = 1.00000e-01
Здесь символ P{.} означает вероятность события. А для квантили B-распределения с параметрами a=5 и b=4:
B(5.000000,4.000000)-распределение
P{ X ≥3.44623e-01} = 9.00000e-01
1. Андерсон Т. Введение в многомерный статистический анализ. - М.: Физматгиз, 1963.
2. Кендалл М., Стьюарт А.. Статистические выводы и связи. - М.: Наука, 1973.
3. Кендалл М., Стьюарт А.. Многомерный статистический анализ и временные ряды. - М.: Наука, 1976.