УДК 519.2

Лемешко Б.Ю., Маклаков А.А.

(Новосибирск)

НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ ПРИ ПРОВЕРКЕ СЛОЖНЫХ ГИПОТЕЗ О СОГЛАСИИ С РАСПРЕДЕЛЕНИЯМИ ЭКСПОНЕНЦИАЛЬНОГО СЕМЕЙСТВА[1]

Методами статистического моделирования исследованы распределения статистик непараметрических критериев типа Колмогорова, типа  и  Мизеса при проверке сложных гипотез о согласии эмпирических данных с распределениями экспоненциального семейства. При различных значениях параметра формы экспоненциального семейства построены и рекомендуются для применения в задачах статистического анализа модели предельных распределений статистик рассматриваемых критериев согласия. Полученные результаты дополняют рекомендации по стандартизации Р 50.1.037-2002 Госстандарта РФ.

1. Введение

Ошибки измерительных приборов и систем, базирующихся на различных физических принципах, часто не удается описать с помощью нормального закона распределения [1]. В таких ситуациях в случае симметричности законов наблюдаемых случайных величин достаточно хорошей моделью оказывается экспоненциальное семейство распределений с плотностью

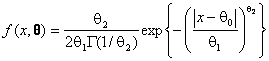.                                        (1)

Частными случаями этого закона при значениях параметра формы , равных 2 и 1, соответственно являются распределения нормальное и Лапласа. Плотности закона при различных значениях параметра формы  приведены на рисунке 1.

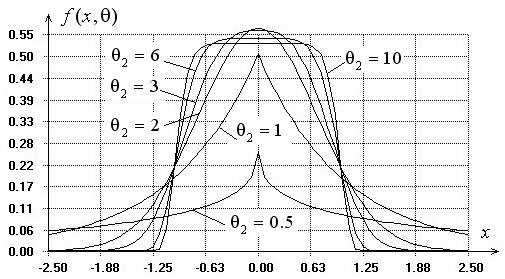
Рис.1. Плотности распределения семейства (1) при различных значениях параметра

Семейство (1) в последнее время достаточно часто используется у качестве вероятностных моделей ошибок наблюдений в задачах регрессионного и дисперсионного анализов при нарушении классических предположений, когда закон распределения ошибок существенно отличается от нормального.

Столкнувшись с необходимостью определения закона распределения ошибок измерений прибора или измерительной системы, ошибок наблюдений при проведении экспериментальных исследований, исследователь должен, опираясь на результаты наблюдений, подобрать модель, наиболее близкую к реальному закону, то есть идентифицировать закон распределения ошибок.  

 Процесс идентификации закона распределения по экспериментальным наблюдениям ошибок измерений (или некоторой другой наблюдаемой случайной величины) реально заключается в решении последовательности задач оценивания параметров вероятностных моделей, проверки адекватности построенных моделей с помощью критериев согласия и последующего выбора на основании этой проверки наиболее подходящего теоретического закона из множества рассматриваемых. 

Проверка согласия полученного опытного распределения с теоретическим является одной из наиболее распространенных задач статистического анализа, решаемой при обработке измерительной информации. Следует подчеркнуть, что до настоящего времени реальная практика применения как непараметрических критериев согласия, так и критериев типа  изобилует примерами некорректного использования. В случае использования непараметрических критериев согласия ошибки, как правило, бывают связаны с тем, что не учитывается фактор сложности проверяемой гипотезы.

 Применяя критерии согласия, следует различать проверку простых и сложных гипотез. Простая проверяемая гипотеза имеет вид : , где  – функция распределения вероятностей, с которой проверяется согласие наблюдаемой выборки, а  – известное значение параметра (векторного или скалярного). При проверке сложной гипотезы проверяемая гипотеза имеет вид : . В этом случае оценка параметра распределения  вычисляется по той же самой выборке, по которой проверяется согласие.

Непараметрические критерии согласия типа Колмогорова, типа  Мизеса (Крамера-Мизеса-Смирнова) и  Андерсона-Дарлинга [2] относятся к наиболее часто используемым критериям согласия. При проверке простых гипотез они являются “свободными от распределения”: условные распределения  статистик  этих критериев не зависят от вида проверяемой гипотезы  (от теоретического закона, с которым проверяется согласие).

В критерии типа Колмогорова используется статистика вида [2]

,                                                                  (2)

где

, , ,

 - объем выборки,  - упорядоченные по возрастанию выборочные значения,  - функция закона распределения, согласие с которым проверяется. Распределение величины  при простой гипотезе в пределе подчиняется закону Колмогорова  [2].

            В критерии типа  Мизеса используется статистика вида [2]

,                                        (3)

которая в случае простой гипотезы подчиняется распределению  [2].

            В критерии типа  Мизеса (Андерсона-Дарлинга) используемая статистика имеет вид [2]

.               (4)

В случае простой гипотезы в пределе эта статистика подчиняется распределению  [2].

При проверке сложных гипотез, когда по той же самой выборке оцениваются параметры наблюдаемого закона , непараметрические критерии согласия теряют свойство “свободы от распределения”. На условный закон распределения статистики при проверке сложных гипотез влияет целый ряд факторов, определяющих “сложность” проверяемой гипотезы : вид наблюдаемого закона , соответствующего истинной гипотезе ; тип оцениваемого параметра; количество оцениваемых параметров; в некоторых ситуациях конкретное значение параметра (например, в случае гамма- и бета-распределений); используемый метод оценивания параметров.

Отличия в предельных распределениях тех же самых статистик при проверке простых и (различных) сложных гипотез настолько существенны, что пренебрегать всеми указанными факторами при использовании непараметрических критериев согласия абсолютно недопустимо.

С момента появления работы [3], в которой была обозначена проблема, связанная с применением непараметрических критериев согласия для проверки сложных гипотез, к исследованию предельных распределений статистик данных критериев применялись различные подходы: предельные распределения исследовались аналитически [4]; процентные точки распределений строились методами статистического моделирования [6-8]; для приближенного вычисления вероятностей “согласия” вида 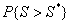 (достигаемого уровня значимости), где 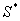 – значение статистики, вычисленное по выборке, строились формулы, дающие достаточно хорошие приближения при малых значениях соответствующих вероятностей [9-13]. Сложность и трудоемкость получения решений аналитическими методами предопределили ограниченность конкретных результатов.

В наших работах [14-20] к задаче исследования распределений статистик непараметрических критериев согласия при проверке сложных гипотез и к построению моделей этих распределений мы подошли с позиций компьютерных методов моделирования и исследования статистических закономерностей [21]. Полученные в совокупности результаты позволили сформировать рекомендации по стандартизации [22], которые существенно расширили область корректного применения непараметрических критериев согласия при проверке различных сложных гипотез. В данной работе мы приводим результаты исследований и построенные модели предельных распределений рассматриваемых критериев для проверки сложных гипотез о согласии эмпирических распределений с теоретическими законами семейства (1) при различных значениях параметра формы .

2. Распределения статистик критериев при проверке согласия с экспоненциальным семейством

Распределения статистик  рассматриваемых непараметрических критериев при проверке согласия с экспоненциальным семейством зависят от всех перечисленных выше факторов, определяющих “сложность” проверяемой гипотезы, в том числе, и от конкретного значения параметра формы . В данном случае непростая задача построения моделей распределений  статистик критериев усугубляется количеством параметров, определяющих закон вида (1). Это означает, что для определенного метода оценивания параметров и для конкретного значения параметра формы  необходимо построить модели распределений статистик при различных комбинациях оцениваемых параметров сдвига , масштаба  и формы  (7 различных видов сложных гипотез).

В данной работе рассматривался только один метод оценивания параметров – метод максимального правдоподобия, который позволяет получать оценки с наилучшими свойствами. При этом оценка максимального правдоподобия (ОМП) параметра  определяется как решение уравнения правдоподобия

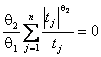,                                                                 (5)

где .  ОМП параметра  находится в качестве решения уравнения правдоподобия вида

,                                                         (6)

а ОМП параметра  – в качестве решения уравнения правдоподобия

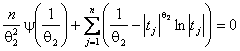,                                          (7)

где  - логарифмическая производная гамма-функции (дигамма-функция).

            При одновременном оценивании нескольких параметров максимизируется логарифм функции правдоподобия

,

и вектор оценок являются решением соответствующей системы (подсистемы) уравнений правдоподобия (5)-(7).

Подчеркнем, что метод оценивания должен обязательно учитываться при проверке сложных гипотез [18]. Как в данном случае зависят распределения статистик от метода оценивания, иллюстрирует рисунок 2.

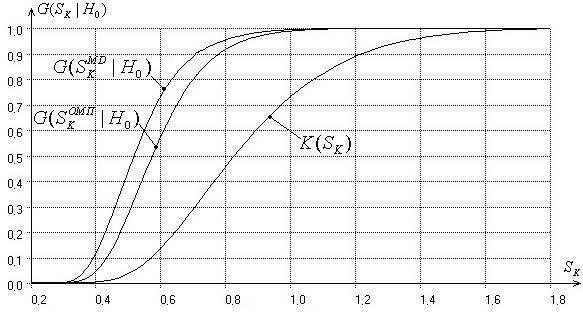
Рис. 2. Распределения статистики типа Колмогорова при оценивании всех параметров закона (1) и использовании ОМП и MD-оценок

На рисунке представлены распределения статистики типа Колмогорова при оценивании всех параметров распределения (1) при значении параметра формы =2 и использовании 2-х методов оценивания: максимального правдоподобия и MD-оценивания, при котором оценка вектора параметров получается минимизацией статистики Колмогорова (2). Для сравнения здесь же приведено распределение Колмогорова, которому подчиняется статистика (2) при проверке простых гипотез.

Статистическое моделирование и исследование получаемых эмпирических распределений статистик (2)-(4) при справедливости гипотезы , соответствующей закону (1), показало существенную и не совсем обычную зависимость распределений статистик  от параметра формы . Как правило, с ростом  от 0 до ≈1.6 происходит уменьшение масштабного параметра распределения статистики , а при дальнейшем росте   – увеличение масштабного параметра. При значениях  > 7  распределения статистик при соответствующих сложных гипотезах практически не меняются.

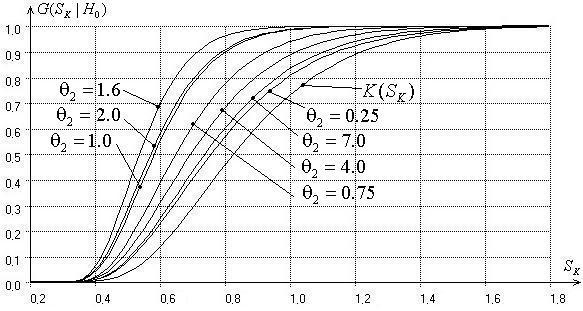
Рис. 3. Зависимость распределения статистики критерия типа Колмогорова от параметра формы  при оценивании всех 3-х параметров распределения (1)

В частности, рисунок 3 иллюстрирует зависимость распределений статистики типа Колмогорова от параметра формы  для случая, когда все три параметра распределения (1) оцениваются методом максимального правдоподобия. На рисунке 4 представлена аналогичная картина, соответствующая оцениванию только 2-х параметров: сдвига  и масштаба  при известном параметре формы .

Рисунок 5 отражает характер зависимости распределения статистики критерия типа Колмогорова от числа и типа параметров, оцениваемых методом максимального правдоподобия, при значении параметра формы =1.6. Этому значению параметра формы соответствуют самые “сдвинутые” влево распределения статистик непараметрических критериев согласия при проверке гипотез относительно закона (1).  На рисунках 5-8 соответствующие распределения  помечены перечнем оцениваемых параметров.

Аналогичная картина для распределений статистики типа  Крамера-Мизеса-Смирнова представлена на рисунке 6. Здесь же для сравнения приведена функция распределения , которой подчиняется статистика в случае проверки простой гипотезы.

Для такой же ситуации на рисунке 7 приведены распределения статистики критерия типа  Андерсона-Дарлинга при проверке сложных гипотез относительно закона (1) при параметре формы =1.6, а также распределение , которому в пределе подчиняется эта же статистика при проверке простых гипотез.

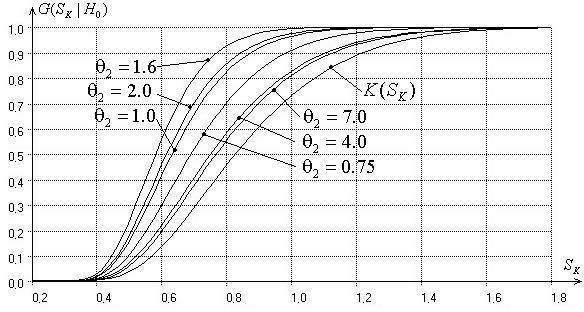
Рис. 4. Зависимость распределения статистики критерия типа Колмогорова от параметра формы  при оценивании только параметров сдвига и масштаба распределения (1)

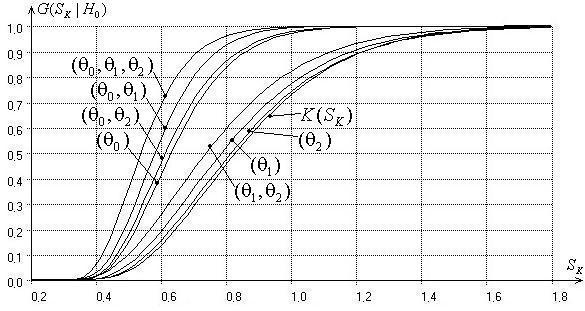
Рис. 5. Зависимость распределения статистики критерия типа Колмогорова от числа и типа оцениваемых методом максимального правдоподобия параметров при значении параметра формы =1.6

Для сравнения на рисунке 8 приведена картина, аналогичная рисунку 5, на которой отражена зависимость распределения статистики критерия типа Колмогорова от числа и типа параметров при значении параметра формы =2. В этом случае плотность (1) соответствует нормальному закону.

Получаемые в результате статистического моделирования эмпирические распределения статистик критериев согласия сглаживались различными теоретическими моделями законов, включенными в систему [21]. В результате подбиралось теоретическое распределение, наилучшим образом описывающее эмпирическое. Как и в предыдущих случаях [14-19], наиболее хорошими аналитическими моделями для распределений  данных статистик чаще всего оказывались модели, соответствующие одному из следующих трех законов: гамма-распределению, распределению Su-Джонсона или распределению Sl-Джонсона.

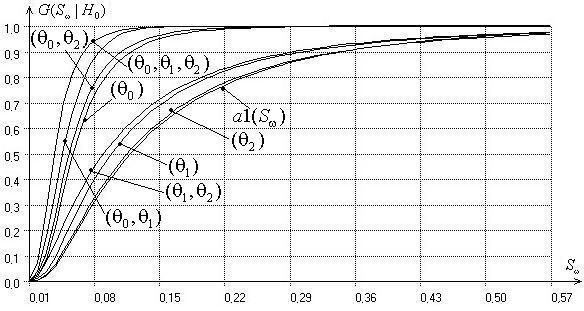
Рис. 6. Зависимость распределения статистики критерия типа  Крамера-Мизеса-Смирнова от числа и типа оцениваемых методом максимального правдоподобия параметров при значении параметра формы =1.6

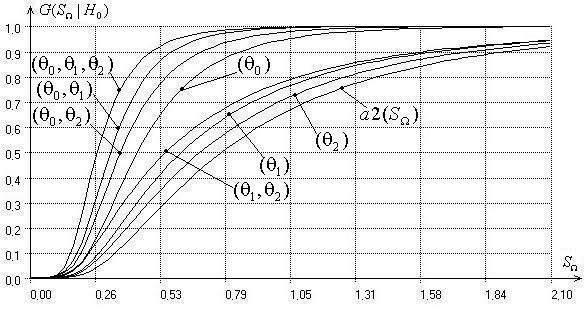
Рис. 7. Зависимость распределения статистики критерия типа  Андерсона-Дарлинга от числа и типа параметров, оцениваемых методом максимального правдоподобия, при значении параметра формы =1.6

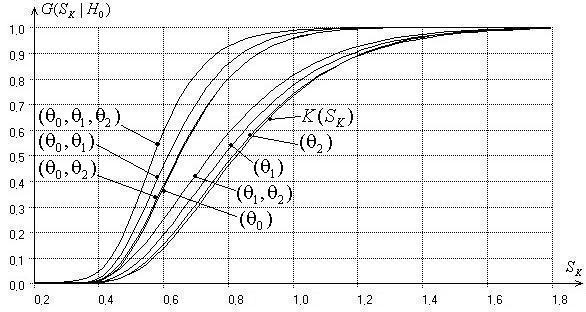
Рис. 8. Зависимость распределения статистики критерия типа Колмогорова от числа и типа оцениваемых методом максимального правдоподобия параметров при значении параметра формы =2

Построенные модели для распределений статистик  критериев типа Колмогорова, Крамера-Мизеса-Смирнова и Андерсона-Дарлинга для проверки сложных гипотез о согласии с экспоненциальным семейством при различных значениях параметра формы  представлены соответственно в таблицах 1-3. В данных таблицах, содержащих полученные и рекомендуемые для использования при проверке сложных гипотез распределения  статистик рассматриваемых критериев, через  обозначено гамма-распределение с функцией плотности

,

через  - распределение Sl-Джонсона с плотностью

,

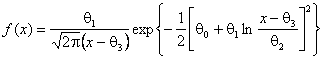через  - распределение Su-Джонсона с плотностью

.

Таблица 1

Аппроксимация предельных распределений статистики Колмогорова при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании только параметра формы	При оценивании только масштабного параметра	При оценивании только параметра сдвига	При оценивании трех параметров (формы, масштаба и сдвига)
1	0.25	g(3,3957; 0,1419; 0,3342)	g(3,2891;0,1454;0,3361)	g(4,1678; 0,1293; 0,3334)	g(3,5003; 0,1370; 0,3229)
2	0.5	g(3,7204; 0,1365; 0,3266)	g(3,5436; 0,1387; 0,3232)	g(3,7577; 0,1336; 0,3448)	g(3,6501; 0,1237; 0,3140)
3	0.75	g(3,7924; 0,1367; 0,3213)	g(3,4892; 0,1396; 0,3319)	g(4,1868; 0,1068; 0,3339)	g(3,9498; 0,0936; 0,3106)
4	1.0	g(3,4680; 0,1467; 0,3428)	g(3,7599; 0,1342; 0,3209)	g(4,1175; 0,0935; 0,3408)	g(4,5150; 0,0689; 0,2945)
5	1.5	g(3,5197; 0,1434; 0,3563)	g(3,9228; 0,1296; 0,3155)	g(4,5449; 0,0741; 0,3173)	g(4,9547; 0,052; 0,2929)
6	1.6	g(3,8275; 0,1375; 0,3336)	g(3,4907; 0,1424; 0,334)	g(5.2114; 0,0676; 0,3011)	g(4,7791; 0,0545; 0,2953)
7	2.0	g(3,5579; 0,1441; 0,3523)	g(3,4864; 0,1424; 0,3371)	g(4,4963; 0,078; 0,3250)	g(4,1586; 0,0714; 0,2989)
8	3.0	g(4,1405; 0,1312; 0,3256)	g(3,5201; 0,1401; 0,3411)	g(4,2098; 0,0971; 0,3311)	g(4,3976; 0,0902; 0,2809)
9	4.0	g(3,9274; 0,1356; 0,3394)	g(3,6132; 0,1393; 0,3432)	g(3,9069; 0,1122; 0,3326)	g(3,9126; 0,1095; 0,3033)
10	5.0	g(3,7127; 0,1407; 0,3518)	g(3,4220; 0,1469; 0,3513)	g(3,9228; 0,1183; 0,3308)	g(3,7199; 0,1180; 0,3113)
11	6.0	g(4,14; 0,1295; 0,3313)	g(3,4004; 0,1478; 0,3507)	g(4,1123; 0,117; 0,328)	g(3,4870; 0,1282; 0,3222)
12	7.0	g(3,9512; 0,1351; 0,3385)	g(3,8910; 0,1351; 0,3254)	g(3,6487; 0,1289; 0,3475)	g(3,6734; 0,1262; 0,317)

Окончание таблицы 1

Аппроксимация предельных распределений статистики Колмогорова при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании двух параметров (формы и масштаба)	При оценивании двух параметров (формы и сдвига)	При оценивании двух параметров (масштаба и сдвига)
1	0,25	g(3,2071; 0,1416; 0,348)	g(3,6141; 0,1345; 0,329)	g(3,2012; 0,1467; 0,3411)
2	0,5	g(3,4833; 0,1330; 0,3117)	g(3,448; 0,135; 0,3433)	g(3,2933; 0,1354; 0,3433)
3	0,75	g(3,741; 0,1310; 0,2925)	g(4,2278; 0,1025; 0,317)	g(4,2809; 0,0956; 0,3132)
4	1,0	g(3,2291; 0,1447; 0,3186)	g(4,6295; 0,0809; 0,3120)	g(4,5961; 0,0760; 0,3084)
5	1,5	g(3,3351; 0,1425; 0,3150)	g(5,3387; 0,0644; 0,2937)	g(4,9614; 0,0588; 0,3066)
6	1,6	g(3,5941; 0,1340; 0,3005)	g(4,4359; 0,0716; 0,3191)	g(6,0113; 0,0529; 0,2807)
7	2,0	g(3,3243; 0,1431; 0,3175)	g(4,4110; 0,0802; 0,3195)	g(4,5532; 0,0722; 0,3106)
8	3,0	g(3,2322; 0,1458; 0,3305)	g(4,2836; 0,0955; 0,3258)	g(3,957; 0,0992; 0,3263)
9	4,0	g(3,5176; 0,1428; 0,3195)	g(3,9688; 0,1097; 0,3368)	g(3,8001; 0,1221; 0,3272)
10	5,0	g(3,8539; 0,1361; 0,3016)	g(3,4492; 0,1275; 0,3547)	g(3,6304; 0,11198; 0,3401)
11	6,0	g(3,2838; 0,1493; 0,3337)	g(4,0420; 0,1189; 0,3308)	g(3,5027; 0,1261; 0,3478)
12	7,0	g(3,3896; 0,1464; 0,3339)	g(3,7526; 0,1276; 0,3419)	g(3,9828; 0,1206; 0,3276)

Таблица 2

Аппроксимация предельных распределений статистики Мизеса при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании только параметра формы	При оценивании только масштабного параметра	При оценивании только параметра сдвига	При оценивании трех параметров (формы, масштаба и сдвига)
1	0.25	Sl(0,9970; 1,0278; 0,2233; 0,0157)	Sl(1,3009; 1,0402; 0,3113; 0,0104)	Sl(0,8362; 1,1012; 0,2234; 0,0125)	Sl(1,5828; 1,0581; 0,3775; 0,0097)
2	0.5	Sl(1,2174; 1,0729; 0,2863; 0,0103)	Sl(0,0880; 1,0126; 0,0926; 0,0121)	Sl(1,0095; 1,1215; 0,2377; 0,0117)	Su(-2,5153; 0,9719; 0,0105; 0,0157)
3	0.75	Sl(1,1095; 1,0685; 0,2635; 0,0114)	Sl(1,1818; 1,0525; 0,2757; 0,0111)	Sl(0,7165; 1,2655; 0,1404; 0,0091)	Su(-2,2482; 1,0158; 0,0097; 0,0169)
4	1.0	Sl(0,1324; 1,0347; 0,1083; 0,0130)	Sl(0,1218; 1,0473; 0,0990; 0,0122)	Su(-2,3848; 1,3757; 0,0188; 0,0173)	Su(-2,1532; 1,2270; 0,0104; 0,0154)
5	1.5	Sl(1,1294; 1,1011; 0,2796; 0,0117)	Sl(0,9558; 1,0559; 0,2173; 0,0125)	Su(-2,2563; 1,3959; 0,0159; 0,0170)	Su(-2,0280; 1,4821; 0,0113; 0,0152)
6	1.6	Sl(1,0768; 1,1009; 0,2770; 0,0114)	Su(-2,4611; 1,0097; 0,0141; 0,0187)	Su(-2,2391; 1,4169; 0,0171; 0,0176)	Su(-1,9635; 1,5327; 0,0132; 0,0151)
7	2.0	Sl(0,1533; 1,1027; 0,1170; 0,0121)	Sl(0,0713; 1,0480; 0,0970; 0,0118)	Su(-2,2789; 1,4329; 0,0190; 0,0164)	Su(-2,1446; 1,3616; 0,0110; 0,0152)
8	3.0	Sl(1,1683; 1,12; 0,3001; 0,0104)	Sl(0,0522; 1,0483; 0,0980; 0,0113)	Su(-2,3109; 1,3327; 0,0212; 0,0184)	Sl(1,1877; 1,1921; 0,1163; 0,0103)
9	4.0	Sl(0,1567; 1,1166; 0,1236; 0,0117)	Sl(0,0646; 1,0404; 0,1021; 0,0128)	Sl(0,8090; 1,2596; 0,1385; 0,0107)	Su(-2,4293; 1,0725; 0,0101; 0,0160)
10	5.0	Sl(0,1610; 1,1007; 0,12; 0,0137)	Sl(0,1120; 1,0821; 0,1085; 0,0118)	Su(-2,3334; 1,2109; 0,0211; 0,0189)	Sl(0,9678; 1,1536; 0,1459; 0,0102)
11	6.0	Sl(1,0459; 1,0951; 0,2698; 0,0137)	Sl(1,13; 1,0799; 0,2783; 0,0116)	Su(-2,4741; 1,2378; 0,0223; 0,0163)	Sl(0,8553; 1,1436; 0,1480; 0,0090)
12	7.0	Sl(1,0257; 1,1205; 0,2652; 0,0122)	Sl(1,0057; 1,1013; 0,2447; 0,0112)	Sl(1,0185; 1,1612; 0,2043; 0,0117)	Sl(0,8799; 1,1287; 0,1593; 0,0089)

Окончание таблицы 2

Аппроксимация предельных распределений статистики Мизеса при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании двух параметров (формы и масштаба)	При оценивании двух параметров (формы и сдвига)	При оценивании двух параметров (масштаба и сдвига)
1	0,25	Sl(1,4204; 1,0381; 0,3432; 0,0113)	Sl(0,9357; 1,0704; 0,2133; 0,0104)	Sl(1,2041; 1,0005; 0,2672; 0,0139)
2	0,5	Sl(1,3181; 0,9793; 0,2937; 0,0124)	Su(-2,4218; 1,0104; 0,0137; 0,0189)	Su(-2,4606; 1,0049; 0,0124; 0,0182)
3	0,75	Sl(1,2082; 1,0205; 0,2651; 0,0086)	Sl(0,8253; 1,2348; 0,1298; 0,0088)	Sl(0,7641; 1,1956; 0,1141; 0,0106)
4	1,0	Sl(0,1625; 0,9807; 0,0950; 0,0106)	Su(-2,1457; 1,4641; 0,0205; 0,0178)	Su(-2,2979; 1,3722; 0,0146; 0,0163)
5	1,5	Sl(1,4317; 1,0457; 0,3333; 0,0077)	Su(-2,2136; 1,4914; 0,0170; 0,0160)	Su(-2,0345; 1,5384; 0,0153; 0,0165)
6	1,6	Sl(1,2852; 1,0206; 0,2884; 0,0085)	Su(-2,2342; 1,4491; 0,0166; 0,0161)	g(2,4197; 0,0163; 0,0119)
7	2,0	Sl(0,1190; 1,0057; 0,0913; 0,0102)	Su(-2,2482; 1,4212; 0,0186; 0,0163)	Su(-2,1977; 1,4459; 0,0160; 0,0161)
8	3,0	Sl(0,1032; 0,9903; 0,0888; 0,0123)	Su(-2,3540; 1,3160; 0,0192; 0,0168)	Sl(0,6710; 1,3212; 0,0916; 0,0092)
9	4,0	Sl(0,1129; 1,0053; 0,0956; 0,0118)	Su(-2,4512; 1,3068; 0,0217; 0,0150)	Sl(0,9618; 1,1902; 0,1428; 0,0111)
10	5,0	Sl(0,1193; 1,0379; 0,0990; 0,0101)	Su(-2,4928; 1,2563; 0,0210; 0,0160)	Sl(0,7066; 1,2649; 0,1307; 0,0074)
11	6,0	Sl(1,1421; 1,0377; 0,263; 0,0109)	Su(-2,4060; 1,2517; 0,0236; 0,0175)	Sl(0,8397; 1,1470; 0,1536; 0,0110)
12	7,0	Sl(1,2261; 1,0383; 0,2870; 0,0115)	Sl(0,7949; 1,1333; 0,1711; 0,0120)	Sl(0,8055; 1,1475; 0,1653; 0,0110)

Таблица 3

Аппроксимация предельных распределений статистики  Мизеса при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании только параметра формы	При оценивании только масштабного параметра	При оценивании только параметра сдвига	При оценивании трех параметров (формы, масштаба и сдвига)
1	0.25	Sl(0,8745; 1,1415; 1,1035; 0,1002)	Sl(1,2310; 1,1339; 1,5755; 0,1026)	Sl(1,0109; 1,2891; 1,4503; 0,0940)	Su(-2,3812; 1,0889; 0,1015; 0,1485)
2	0.5	Su(-2,5811; 1,0889; 0,0908; 0,1502)	Su(-2,4437; 1,0649; 0,0919; 0,1550)	Sl(0,9215; 1,1284; 1,2930; 0,1159)	Sl(1,0190; 1,0398; 1,1220; 0,1135)
3	0.75	Sl(1,0242; 1,1631; 1,3162; 0,1026)	Su(-2,4034; 1,0931; 0,1025; 0,1527)	Sl(0,8710; 1,3996; 1,0112; 0,0804)	Su(-2,1784; 1,1030; 0,0802; 0,1439)
4	1.0	Su(-2,9616; 1,1617; 0,0850; 0,1204)	Su(-2,4983; 1,0832; 0,0911; 0,1548)	Su(-2,1865; 1,5178; 0,1810; 0,1669)	Su(-2,1179; 1,3890; 0,0939; 0,1309)
5	1.5	Sl(1,0533; 1,1878; 1,4052; 0,105)	Su(-2,4417; 1,1123; 0,1039; 0,1547)	Su(-2,0561; 1,4573; 0,1450; 0,1605)	Su(-2,0642; 1,5304; 0,0864; 0,1192)
6	1.6	Sl(0,9294; 1,2394; 1,2802; 0,0838)	Su(-2,4245; 1,0923; 0,1007; 0,1545)	Su(-2,1491; 1,5130; 0,1476; 0,1458)	Su(-1,9792; 1,4810; 0,0822; 0,1255)
7	2.0	Sl(0,8791; 1,2097; 1,2371; 0,1054)	Sl(0,5880; 1,0827; 0,8719; 0,1221)	Su(-2,2029; 1,4414; 0,1313; 0,1517)	Su(-2,0023; 1,4458; 0,0809; 0,1269)
8	3.0	Su(-2,9061; 1,2003; 0,1029; 0,140)	Su(-2,6636; 1,1316; 0,0915; 0,1454)	Su(-2,1666; 1,4595; 0,160; 0,1518)	Su(-2,27; 1,2970; 0,0723; 0,1228)
9	4.0	Su(-3,0980; 1,2257; 0,1032; 0,1255)	Su(-2,687; 1,1707; 0,1035; 0,14125)	Su(-2,2756; 1,4168; 0,1677; 0,1415)	Su(-2,3153; 1,1754; 0,0707; 0,1256)
10	5.0	Su(-3,1001; 1,2525; 0,1104; 0,1214)	Su(-2,7074; 1,1463; 0,1003; 0,141)	Su(-2,3443; 1,3488; 0,1511; 0,1536)	Sl(0,5525; 1,2411; 0,5018; 0,0831)
11	6.0	Sl(0,8671; 1,1959; 1,2956; 0,1158)	Sl(1,0228; 1,1518; 1,3609; 0,1083)	Su(-2,3719; 1,3537; 0,1623; 0,1462)	Sl(0,5166; 1,2025; 0,5222; 0,0882)
12	7.0	Sl(1,1286; 1,2642; 1,6235; 0,0929)	Sl(0,9102; 1,2147; 1,2198; 0,0939)	Sl(0,6061; 1,2797; 0,7946; 0,0980)	Su(-2,4112; 1,1873; 0,0905; 0,1194)

Окончание таблицы 3

Аппроксимация предельных распределений статистики  Мизеса при проверке согласия с классом экспоненциальных распределений и использовании метода максимального правдоподобия
№ п/п	Значение параметра формы	При оценивании двух параметров (формы и масштаба)	При оценивании двух параметров (формы и сдвига)	При оценивании двух параметров (масштаба и сдвига)
1	0,25	Sl(1,0488; 1,0925; 1,2482; 0,0932)	Su(-2,3820; 1,1381; 0,1180; 0,1536)	Su(-2,4011; 1,0665; 0,0952; 0,1462)
2	0,5	Su(-2,4405; 1,0159; 0,0752; 0,1457)	Sl(1,2511; 1,14; 1,4661; 0,1067)	Su(-2,3619; 1,0352; 0,0814; 0,1621)
3	0,75	Sl(1,0707; 1,0907; 1,2632; 0,0941)	Su(-2,3367; 1,2714; 0,1190; 0,1369)	Su(-2,2040; 1,1573; 0,0965; 0,1602)
4	1,0	Su(-2,3917; 0,9957; 0,0772; 0,1414)	Su(-2,0747; 1,4923; 0,1427; 0,1533)	Su(-1,9642; 1,4128; 0,1289; 0,1568)
5	1,5	Su(-2,3473; 1,0625; 0,0970; 0,1335)	Su(-2,1035; 1,5579; 0,1265; 0,1432)	Su(-1,9488; 1,5350; 0,1071; 0,1406)
6	1,6	Su(-2,4953; 1,0236; 0,0736; 0,1305)	Su(-2,0957; 1,5279; 0,1241; 0,1367)	Su(-1,9403; 1,6314; 0,1232; 0,1409)
7	2,0	Su(-2,3736; 0,9870; 0,0734; 0,1472)	Su(-2,2201; 1,4813; 0,1249; 0,1282)	Su(-2,0349; 1,5403; 0,1173; 0,1372)
8	3,0	Sl(0,9651; 1,1157; 1,1347; 0,0897)	Su(-2,2047; 1,4; 0,1345; 0,1419)	Su(-2,2749; 1,4149; 0,1095; 0,1322)
9	4,0	Su(-2,5015; 1,0159; 0,0756; 0,1424)	Sl(0,6802; 1,3306; 0,6817; 0,0929)	Su(-2,2539; 1,2894; 0,1055; 0,1412)
10	5,0	Su(-2,4061; 1,0454; 0,0935; 0,1373)	Su(-2,3961; 1,3816; 0,1552; 0,1271)	Sl(0,6031; 1,3879; 0,6263; 0,0702)
11	6,0	Sl(1,0578; 1,1194; 1,2773; 0,0968)	Su(-2,3468; 1,3099; 0,1467; 0,1363)	Su(-2,3690; 1,2866; 0,1221; 0,1339)
12	7,0	Sl(1,2054; 1,1242; 1,5073; 0,0980)	Su(-2,4149; 1,2619; 0,1381; 0,1385)	Sl(0,6352; 1,1862; 0,7252; 0,1065)

3. Применение результатов

В процессе проверки гипотезы о согласии эмпирического распределения с теоретическим по выборке вычисляется значение  статистики используемого критерия. Затем для того, чтобы сделать вывод о том, принять или отклонить гипотезу , необходимо, зная условное распределение  статистики  при справедливости , вычислить вероятность

,

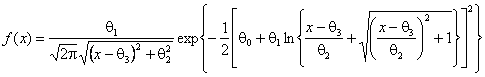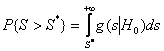где  – условная плотность. Если эта вероятность достаточно большая, по крайней мере , где  – задаваемый уровень значимости (вероятность ошибки первого рода – отклонить справедливую гипотезу ), то принято считать, что нет оснований для отклонения гипотезы .

            Рассмотрим использование полученных результатов при проверке сложных гипотез на следующем примере.

Пример. Пусть проверяется гипотеза о принадлежности выборки из 100 наблюдений

-1.17    -1.09    -0.91    -0.90    -0.89    -0.88    -0.86    -0.85    -0.85    -0.75

-0.73    -0.66    -0.64    -0.58    -0.58    -0.55    -0.54    -0.53    -0.52    -0.50

-0.50    -0.50    -0.47    -0.45    -0.44    -0.42    -0.41    -0.41    -0.40    -0.40

-0.39    -0.38    -0.37    -0.30    -0.30    -0.29    -0.28    -0.24    -0.23    -0.21

-0.20    -0.18    -0.17    -0.16    -0.15    -0.15    -0.13    -0.09    -0.05    -0.05

-0.03    -0.02    0.00    0.02    0.05    0.08    0.10    0.11    0.11    0.14

 0.15    0.16    0.18    0.25    0.25    0.26    0.27    0.28    0.30    0.33

 0.33    0.36    0.40    0.41    0.42    0.43    0.44    0.48    0.51    0.52

 0.53    0.54    0.55    0.58    0.61    0.63    0.68    0.69    0.71    0.72

 0.74    0.76    0.79    0.80    0.88    0.96    0.96    0.97    1.12    1.39

экспоненциальному семейству с известным параметром формы . Вычисленные по данной выборке ОМП параметров сдвига и масштаба соответственно равны  и . На рисунке 9 отражены построенная по выборке эмпирическая функция распределения и теоретическая функция распределения закона (1) с полученным вектором параметров.

Рис. 9. Теоретическая и эмпирическая функции распределения

Проверим гипотезу о согласии по всем рассматриваемым в работе критериям. В данном случае проверяется сложная гипотеза с оцениванием методом максимального правдоподобия параметров сдвига и масштаба. Вычисленные по выборке значения статистик оказались равными: статистика (2) Колмогорова ; статистика (3) Крамера-Мизеса-Смирнова ; статистика (4) Андерсона-Дарлинга .

 Вычисленное в соответствии с гамма-распределением g(3,8001; 0,1221; 0,3272) (см. таблицу 1 при значении параметра формы ) значение вероятности  для критерия типа Колмогорова говорит о хорошем согласии выборки с теоретическим распределением.

Аналогично, для статистики  Крамера-Мизеса-Смирнова в соответствии с распределением Sl-Джонсона Sl(0,9618; 1,1902; 0,1428; 0,0111) (см. таблицу 2) находим значение вероятности . А для статистики Андерсона-Дарлинга (см. таблицу 3) в соответствии с распределением Su-Джонсона Su(-2,2539; 1,2894; 0,1055; 0,1412) вычисляем значение вероятности .

Таким образом, по всем критериям подтверждается хорошее согласие анализируемой выборки с теоретической моделью вида (1).

4. Заключение

Опираясь на компьютерные методы исследования статистических закономерностей, в основе которых лежит статистическое моделирование эмпирических распределений статистик, последующий анализ этих распределений и построение для них простых аналитических моделей, исследованы распределения статистик критериев согласия типа Колмогорова, типа  Крамера-Мизеса-Смирнова и типа  Андерсона-Дарлинга.

Получены модели предельных распределений данных статистик при проверке сложных гипотез в случае оценивания методом максимального правдоподобия различных комбинаций параметров экспоненциального семейства распределений. Такие модели получены для различных значений параметра формы .

Построенные аппроксимации предельных распределений статистик непараметрических критериев расширяют рекомендации по стандартизации [22] и позволяют корректно применять данные критерии для проверки адекватности моделей вида (1), используемых для описания ошибок измерительных систем и в других задачах статистического анализа наблюдений.

Литература

1. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомиздат, 1991. – 303 с.

2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

3. Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat. – 1955. – V.26. – P.189-211.

4. Мартынов Г.В. Критерии омега–квадрат. – М.: Наука, 1978. – 80 с.

5. Pearson E.S., Hartley H.O. Biometrica tables for Statistics. V.2. – Cambridge: University Press, 1972. – 634 p.

6. Stephens M.A. Use of Kolmogorov–Smirnov, Cramer – von Mises and related statistics – vithout extensive table // J. R. Stat. Soc. – 1970. – B. 32. – P. 115-122.

7. Stephens M.A. EDF statistics for goodness of fit and some comparisons // J. Am. Statist. Assoc. – 1974. – V.69. – P. 730-737.

8. Chandra M., Singpurwalla N.D., Stephens M.A. Statistics for Test of Fit for the Extrem-Value and Weibull Distribution // J. Am. Statist. Assoc. – 1981. – V.76. – P. 375.

9. Тюрин Ю.Н. О предельном распределении статистик Колмогорова–Смирнова для сложной гипотезы // Изв. АН СССР. Сер. Матем. – 1984. – Т. 48. – № 6. – C. 1314-1343.

10. Тюрин Ю.Н., Саввушкина Н.Е. Критерии согласия для распределения Вейбулла–Гнеденко. // Изв. АН СССР. Сер. Техн. Кибернетика. – 1984. – № 3. – C. 109-112.

11. Тюрин Ю.Н. Исследования по непараметрической статистике (непараметрические методы и линейная модель): Автореф. дисс. … д-ра физ.-мат. наук. – М., 1985. – 33 с. – (МГУ).

12. Саввушкина Н.Е. Критерий Колмогорова-Смирнова для логистического и гамма–распределения // Сб. тр. ВНИИ систем. исслед. – 1990, № 8.

13. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. // М.: ИНФРА–М, Финансы и статистика, 1995. – 384 с.

14. Лемешко Б.Ю., Постовалов С.Н. Прикладные аспекты использования критериев согласия в случае проверки сложных гипотез // Надежность и контроль качества. – 1997. – № 11. – С. 3-17.

15. Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. – 1998. – Т. 64. – № 3. – С. 61-72.

16. Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ. – 1999. – 86 с.

17. Лемешко Б.Ю., Постовалов С.Н. Применение непараметрических критериев согласия при проверке сложных гипотез // Автометрия. 2001. – № 2. – С. 88-102.

18. Лемешко Б.Ю., Постовалов С.Н. О зависимости распределений статистик непараметрических критериев и их мощности от метода оценивания параметров // Заводская лаборатория. Диагностика материалов. 2001. Т. 67. – № 7. – С. 62-71.

19. Лемешко Б.Ю., Постовалов С.Н. Непараметрические критерии при проверке сложных гипотез о согласии с распределениями Джонсона // Доклады СО АН ВШ. 2002. – № 1(5). – С.65-74.

20. Лемешко Б.Ю., Постовалов С.Н., Французов А.В. К применению непараметрических критериев согласия для проверки адекватности непараметрических моделей // Автометрия. 2002. – № 2. – С.3-14.

21. Лемешко Б.Ю., Постовалов С.Н. Система статистического анализа наблюдений и исследования статистических закономерностей // Сб. "Моделирование, автоматизация и оптимизация наукоемких технологий". – Новосибирск: изд-во НГТУ, 2000. – С. 44-46.

22. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. – М.: Изд-во стандартов. 2002. – 64 с.

---

[1] Работа выполнена при поддержке Минобразования РФ (проект № ТО2-3.3-3356)