Поиск ассоциативных правил в Data Mining
Введение
Развитие компьютерных технологий послужило
значительному увеличению объема хранимых данных. Это в свою очередь привело к
тому, что человеку стало все труднее
проанализировать их. Хотя необходимость проведения такого анализа вполне очевидна,
ведь в этих 'сырых данных' заключены знания, которые могут быть использованы
при принятии решений. Поэтому стали развиваться методы, позволяющие проводить
автоматический анализ данных.
Data Mining – это процесс обнаружения в 'сырых' данных
ранее неизвестных нетривиальных практически полезных и доступных интерпретации
знаний, необходимых для принятия решений в различных сферах человеческой
деятельности.
Информация, найденная в
процессе применения методов Data Mining, должна быть нетривиальной и ранее неизвестной,
например, средние продажи не являются таковыми. Знания должны описывать новые
связи между свойствами, предсказывать значения одних признаков на основе других
и т.д. Найденные знания должны быть применимы и на новых данных с некоторой
степенью достоверности. Полезность заключается в том, чтобы эти знания могли
принести определенную выгоду при их применении. Знания должны быть в понятном
для пользователя-нематематика виде. Например, проще всего воспринимаются
человеком логические конструкции 'если … то …'. Более того, такие правила могут
быть использованы в различных СУБД в качестве SQL-запросов. В случае, когда
извлеченные знания непрозрачны для пользователя, должны существовать методы
постобработки, позволяющие привести их к интерпретируемому виду. Алгоритмы,
используемые в Data Mining, требуют большого количества вычислений. Раньше это
являлось сдерживающим фактором широкого практического применения Data Mining,
однако сегодняшний рост производительности современных процессоров снял остроту
этой проблемы. Теперь за приемлемое время можно провести качественный анализ
сотен тысяч и миллионов записей.
Для решения данных задач
используются различные методы и алгоритмы Data Mining. Большую популярность
получили следующие методы Data Mining: нейронные сети, деревья решений,
алгоритмы кластеризации, в том числе и масштабируемые, алгоритмы обнаружения
ассоциативных связей между событиями и т.д.
1. Введение в анализ ассоциативных правил
В последнее время неуклонно растет интерес к
методам 'обнаружения знаний в базах данных'. Объемы современных баз данных,
которые весьма внушительны, вызвали устойчивый спрос на новые масштабируемые
алгоритмы анализа данных. Одним из популярных методов обнаружения знаний стали
алгоритмы поиска ассоциативных правил.
Ассоциативные правила позволяют находить
закономерности между связанными событиями. Примером такого правила, служит
утверждение, что покупатель, приобретающий 'Хлеб', приобретет и 'Молоко' с
вероятностью 72%. Первый алгоритм поиска
ассоциативных правил, называвшийся AIS
был разработан в 1993 году сотрудниками исследовательского центра IBM
Almaden. С этой пионерской работы возрос интерес к ассоциативным правилам; на
середину 90-х годов прошлого века пришелся пик исследовательских работ в этой
области, и с тех пор каждый год появлялось по несколько алгоритмов.
1.1 Ассоциативные правила
Впервые это задача была предложена поиска ассоциативных
правил для нахождения типичных шаблонов покупок, совершаемых в супермаркетах,
поэтому иногда ее еще называют анализом рыночной корзины (market basket
analysis).
Пусть имеется база данных, состоящая из покупательских
транзакций. Каждая транзакция – это набор товаров, купленных покупателем
за один визит. Такую транзакцию еще называют рыночной корзиной.
Пусть I = {i1, i2, i3, …in} –
множество (набор) товаров, называемых элементами. Пусть D – множество
транзакций, где каждая транзакция T – это набор элементов из I, T 
I. Каждая
транзакция представляет собой бинарный вектор, где t[k]=1, если ik
элемент присутствует в транзакции, иначе t[k]=0. Мы говорим, что транзакция T
содержит X, некоторый набор элементов из I, если X T.
Ассоциативным правилом называется импликация X 
Y, где X 
I, Y I и X 
Y = 
. Правило X Y имеет
поддержку s (support), если s% транзакций из D, содержат X 
Y, supp(X Y) = supp (X
Y).
Достоверность правила показывает какова вероятность того, что из X следует Y.
Правило X Y
справедливо с достоверностью (confidence) c, если c% транзакций из D,
содержащих X, также содержат Y, conf(X Y) = supp(X Y)/supp(X ).
Покажем на конкретном
примере: '75% транзакций, содержащих хлеб, также содержат молоко. 3% от общего
числа всех транзакций содержат оба товара'. 75% – это достоверность (confidence)
правила, 3% это поддержка (support), или 'Хлеб' 'Молоко' с
вероятностью 75%. Другими словами, целью анализа является установление
следующих зависимостей: если в транзакции встретился некоторый набор элементов
X, то на основании этого можно сделать вывод о том, что другой набор элементов
Y также же должен появиться в этой транзакции. Установление таких зависимостей
дает нам возможность находить очень простые и интуитивно понятные правила.
Алгоритмы поиска ассоциативных правил предназначены для нахождения
всех правил X Y, причем
поддержка и достоверность этих правил должны быть выше некоторых наперед
определенных порогов, называемых соответственно минимальной поддержкой
(minsupport) и минимальной достоверностью (minconfidence).
Задача нахождения ассоциативных правил разбивается на две
подзадачи:
1. Нахождение всех наборов элементов, которые
удовлетворяют порогу minsupport. Такие наборы элементов называются часто
встречающимися.
2. Генерация правил из наборов элементов,
найденных согласно п.1. с достоверностью, удовлетворяющей порогу minconfidence.
Значения для параметров
минимальная поддержка и минимальная достоверность выбираются таким образом,
чтобы ограничить количество найденных правил. Если поддержка имеет большое
значение, то алгоритмы будут находить правила, хорошо известные аналитикам или
настолько очевидные, что нет никакого смысла проводить такой анализ. С другой
стороны, низкое значение поддержки ведет к генерации огромного количества
правил, что, конечно, требует существенных вычислительных ресурсов. Тем не
менее, большинство интересных правил находится именно при низком значении
порога поддержки. Хотя слишком низкое значение поддержки ведет к генерации
статистически необоснованных правил.
Поиск
ассоциативных правил совсем не тривиальная задача, как может показаться на
первый взгляд. Одна из проблем – алгоритмическая сложность при нахождении
часто встречающих наборов элементов, т.к. с ростом числа элементов в I (| I |)
экспоненциально растет число потенциальных наборов элементов.
1.2 Свойство анти-монотонности
Выявление часто
встречающихся наборов элементов – операция, требующая много вычислительных
ресурсов и, соответственно, времени. Примитивный подход к решению данной
задачи – простой перебор всех возможных наборов элементов. Это потребует
O(2|I|) операций, где |I| – количество элементов. Поэтому
используют одно из свойств поддержки, гласящее: поддержка любого набора элементов не может превышать минимальной
поддержки любого из его подмножеств. Например, поддержка 3-элементного
набора {Хлеб, Масло, Молоко} будет всегда меньше или равна поддержке
2-элементных наборов {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко}. Дело в
том, что любая транзакция, содержащая {Хлеб, Масло, Молоко}, также должна
содержать {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко}, причем обратное не верно.
Это свойство носит название анти-монотонности и служит для снижения размерности
пространства поиска.
Свойству
анти-монотонности можно дать и другую формулировку: с ростом размера набора
элементов поддержка уменьшается, либо остается такой же. Из всего
вышесказанного следует, что любой k-элементный набор будет часто встречающимся
тогда и только тогда, когда все его (k-1)-элементные подмножества будут часто
встречающимися. Все возможные наборы элементов из I можно представить в виде
решетки, начинающейся с пустого множества, затем на 1 уровне 1-элементные
наборы, на 2-м – 2-элементные и т.д. На k уровне представлены k-элементные
наборы, связанные со всеми своими (k-1)-элементными подмножествами. Рассмотрим
Рис.1, иллюстрирующий набор элементов I – {A, B, C, D}. Предположим, что
набор из элементов {A, B} имеет поддержку ниже заданного порога и,
соответственно, не является часто встречающимся. Тогда, согласно свойству
анти-монотонности, все его супермножества также не являются часто
встречающимися и отбрасываются. Вся эта ветвь, начиная с {A, B}, отмечена
желтым фоном. Использование этой эвристики позволяет существенно сократить
пространство поиска.
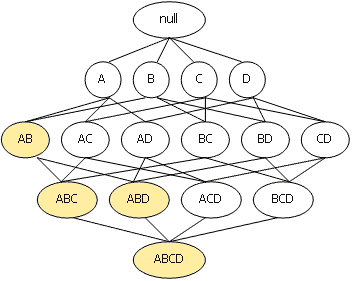
Рис. 1
1.3 Обобщенные ассоциативные правила
При поиске ассоциативных правил, мы
предполагали, что все анализируемые элементы однородны. Возвращаясь к анализу
рыночной корзины, это товары, имеющие совершенно одинаковые атрибуты, за
исключением названия. Однако не составит большого труда дополнить транзакцию
информацией о том, в какую товарную группу входит товар и построить иерархию
товаров. Приведем пример такой группировки (таксономии) в виде иерархической
модели.
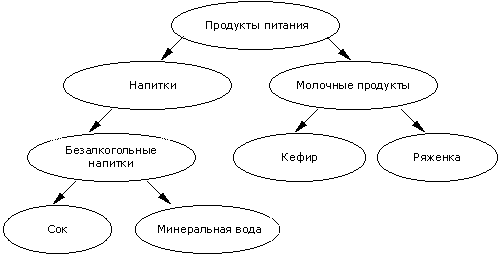
Рис. 2
Пусть нам дана база транзакций D и известно в
какие группы (таксоны) входят элементы. Тогда можно извлекать из данных
правила, связывающие группы с группами, отдельные элементы с группами и т.д. Например,
если Покупатель купил товар из группы 'Безалкогольные напитки', то он купит и
товар из группы 'Молочные продукты' или 'Сок' 'Молочные
продукты'. Эти правила носят название обобщенных ассоциативных правил.
Обобщенным
ассоциативным правилом называется импликация X Y, где X I, Y I и X Y= и где ни
один из элементов, входящих в набор Y, не является предком ни одного элемента,
входящего в X. Поддержка и достоверность подсчитываются так же, как и в случае
ассоциативных правил (см. Определение 1).
Введение дополнительной
информации о группировке элементов в виде иерархии даст следующие преимущества:
1. Это помогает установить ассоциативные
правила не только между отдельными элементами, но и между различными уровнями
иерархии (группами).
2. Отдельные элементы могут иметь
недостаточную поддержку, но в целом группа может удовлетворять порогу
minsupport.
Для нахождения таких правил нужно каждую
транзакцию нужно дополнить всеми предками каждого элемента, входящего в
транзакцию. Однако, применение 'в лоб' этих алгоритмов неизбежно приведет к
следующим проблемам:
1. Элементы на верхних уровнях иерархии
стремятся к значительно большим значениям поддержки по сравнению с элементами
на нижних уровнях.
2. С добавлением в транзакции групп
увеличилось количество атрибутов и соответственно размерность входного
пространства. Это усложняет задачу, а также ведет к генерации большего
количества правил.
3. Появление избыточных правил,
противоречащих определению обобщенного ассоциативного правила, например, 'Сок' 'Прохладительные
напитки'. Очевидно, что практическая ценность такого 'открытия' нулевая при
100% достоверности. Следовательно, нужны специальные операторы, удаляющие
подобные избыточные правила.
Группировать элементы можно не только по
вхождению в определенную товарную группу, но и по другим характеристикам,
например по цене (дешево, дорого), брэнду и т.д.
1.4 Определение 'интересных' правил
Для решения задачи, поиска 'излишних' обобщенных
ассоциативных правил применяется такой параметр правила как уровень интереса.
Пусть Z –
это предок Z, где Z и Z – множества элементов, входящих в иерархию
(Z,Z 
I). Z
является предком Z, только в том случае, если Z можно получить из Z
путем подмены одного или нескольких элементов их предками. Если рассматривать
иерархию на рис. 2, то примером могут быть эти два множества: Z={Сок, Кефир,
Бумага}, Z={Напитки, Молочные продукты, Бумага}. Будем называть правила X
Y, X Y, X
Y
предками правила X Y.
Правило X 
Y
является ближайшим предком правила X 
Y, если не
существует такого правила X' Y', что X' Y' –
это предок X Y и X
Y –
это предок X' Y'.
Рассмотрим
правило X Y. Пусть Z =
X 
Y. Заметим
что supp(X Y) =
supp(Z). Назовем 
ожидаемым значением Pr(Z) относительно Z.
Пусть Z={z1, …, zn}, Z={z1, …, zj,
zj+1, …, zn}, 
. Тогда можно определить:
Аналогично
определим
как ожидаемое значение достоверности правила X 
Y
относительно X 
Y.
Пусть Y={y1, …, yn}, Y={y1, …, yj,
yj+1…, yn},
. Тогда можно определить
Пример. Пусть в результате
работы алгоритмы мы получили следующие правила (табл. 1). Поддержка элементов
входящих в них приведена в таблице 2. Иерархия элементов дана рис. 2. Уровень
интереса R=1.3.
Таблица 1. Обобщенные ассоциативные правила.
|
N правила |
Текст правила |
Поддержка, % |
|
1 |
Сок |
10 |
|
2 |
Безалкогольные напитки |
15 |
|
3 |
Сок |
9 |
Таблица 2. Поддержка элементов.
|
Элемент |
Поддержка, % |
|
Напитки |
7 |
|
Безалкогольные напитки |
5 |
|
Сок |
3 |
|
Молочные продукты |
6 |
|
Кефир |
4 |
Рассмотрим правило номер 3. Определим является
ли это правило интересным или нет. Другими словами, нам необходимо проверить
неравенство
Правило
2 является ближним предком правила 3, посчитаем ожидаемую поддержку.
Неравенство
не
выполняется, следовательно, правило 3 не является интересным.
1.5 Численные ассоциативные правила
При поиске ассоциативных правил задача была
существенно упрощена. По сути все сводилось к тому, присутствует в транзакции
элемент или нет. Т.е. если рассматривать случай рыночной корзины, то мы
рассматривали два состояния: куплен товар или нет, проигнорировав, например,
информацию о том, сколько было куплено, кто купил, характеристики покупателя и
т.д. И можно сказать, что рассматривали 'булевские' ассоциативные правила. Если
взять любую базу данных, каждая транзакция состоит из различных типов данных:
числовых, категориальных и т.д. Для обработки таких записей и извлечения
численных ассоциативных правил также были предложены алгоритм поиска.
Пример численного ассоциативного правила:
[Возраст: 30-35] и [Семейное положение: женат] [Месячный
доход: 1000-1500 тугриков].
Помимо описанных выше ассоциативных правил существуют косвенные
ассоциативные правила, ассоциативные правила c отрицанием, временные
ассоциативные правила для событий связанных во времени и другие.
2. Алгоритмы
Рассмотрев
ассоциативные правила, перейдем к описанию алгоритмов их реализации.
2.1 Apriori -- масштабируемый алгоритм поиска
ассоциативных правил
Современные базы данных
имеют очень большие размеры, достигающие гига- и терабайтов, и тенденцию к
дальнейшему увеличению. И поэтому, для нахождения ассоциативных правил
требуются эффективные масштабируемые алгоритмы, позволяющие решить задачу за
приемлемое время. Одним из таких алгоритмов является алгоритм Apriori.
Для того, чтобы было
возможно применить алгоритм, необходимо провести предобработку данных:
во-первых, привести все данные к бинарному виду; во-вторых, изменить структуру
данных.
Обычный
вид базы данных транзакций:
Таблица 3
|
Номер транзакции |
Наименование элемента |
Количество |
|
1001 |
А |
2 |
|
1001 |
D |
3 |
|
1001 |
E |
1 |
|
1002 |
А |
2 |
|
1002 |
F |
1 |
|
1003 |
B |
2 |
|
1003 |
A |
2 |
|
1003 |
C |
2 |
|
… |
… |
… |
Нормализованный
вид:
Таблица 4
|
TID |
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
… |
|
1001 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
… |
|
1002 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
… |
|
1003 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
… |
Количество
столбцов в таблице равно количеству элементов, присутствующих в множестве
транзакций D. Каждая запись соответствует транзакции, где в соответствующем
столбце стоит 1, если элемент присутствует в транзакции, и 0 в противном
случае. Заметим, что исходный вид таблицы может быть отличным от приведенного в
таблице 3. Главное, чтобы данные были преобразованы к нормализованному виду,
иначе алгоритм не применим. Кроме того, все элементы должны быть упорядочены в
алфавитном порядке (если это числа, они должны быть упорядочены в числовом
порядке).
Алгоритм
Apriori работает в два этапа: на первом шаге необходимо
найти часто встречающиеся наборы элементов, а затем, на втором, извлечь из них
правила. Количество элементов в наборе будем называть размером набора, а набор,
состоящий из k элементов, – k-элементным набором.
На первом шаге алгоритма подсчитываются 1-элементные часто
встречающиеся наборы. Для этого необходимо пройтись по всему набору данных и
подсчитать для них поддержку, т.е. сколько раз встречается в базе. Следующие
шаги будут состоять из двух частей: генерации потенциально часто встречающихся
наборов элементов (их называют кандидатами) и подсчета поддержки для
кандидатов.
Описанный
выше алгоритм можно записать в виде следующего псевдокода:
1. F1 = {часто встречающиеся 1-элементные
наборы}
2. для (k=2; Fk-1 <> ; k++) {
3. Ck = Apriorigen(Fk-1) //
генерация кандидатов
4. для всех транзакций t 
T {
5. Ct = subset(Ck,
t) // удаление избыточных правил
6. для всех кандидатов c Ct
7. c.count ++
8. }
9. Fk = { c Ck | c.count
>= minsupport} // отбор кандидатов
10. Результат U Fk
Опишем функцию генерации кандидатов. На
это раз нет никакой необходимости вновь обращаться к базе данных. Для того,
чтобы получить k-элементные наборы, воспользуемся (k-1)-элементными наборами,
которые были определены на предыдущем шаге и являются часто встречающимися.
Вспомним, что наш
исходный набор хранится в упорядоченном виде. Генерация кандидатов также будет
состоять из двух шагов.
1. Объединение. Каждый кандидат Ck будет
формироваться путем расширения часто встречающегося набора размера (k-1)
добавлением элемента из другого (k-1)- элементного набора. Приведем алгоритм
этой функции Apriorigen в виде небольшого SQL-подобного запроса:
INSERT
into Ck
SELECT
p.item1,
p.item2, …, p.itemk-1, q.itemk-1
FROM
Fk-1 p, Fk-1
q
WHERE
p.item1= q.item1,
p.item2 = q.item2, … , p.itemk-2 = q.itemk-2,
p.itemk-1 < q.itemk-1
2. Удаление избыточных правил. На основании свойства
анти-монотонности, следует удалить все наборы c 
Ck
если хотя бы одно из его (k-1) подмножеств не является часто встречающимся.
После генерации
кандидатов следующей задачей является подсчет поддержки для каждого кандидата.
Очевидно, что количество кандидатов может быть очень большим и нужен
эффективный способ подсчета. Самый тривиальный способ – сравнить каждую
транзакцию с каждым кандидатом. Но это далеко не лучшее решение. Гораздо
быстрее и эффективнее использовать подход, основанный на хранении кандидатов в
хэш-дереве. Внутренние узлы дерева содержат хэш-таблицы с указателями на
потомков, а листья – на кандидатов. Это дерево нам пригодится для быстрого
подсчета поддержки для кандидатов.
Хэш-дерево строится
каждый раз, когда формируются кандидаты. Первоначально дерево состоит только из
корня, который является листом, и не содержит никаких кандидатов-наборов.
Каждый раз, когда формируется новый кандидат, он заносится в корень дерева и
так до тех пор, пока количество кандидатов в корне-листе не превысит некоего
порога. Как только количество кандидатов становится больше порога, корень
преобразуется в хэш-таблицу, т.е. становится внутренним узлом, и для него
создаются потомки-листья. И все примеры распределяются по узлам-потомкам
согласно хэш-значениям элементов, входящих в набор, и т.д. Каждый новый
кандидат хэшируется на внутренних узлах, пока он не достигнет первого
узла-листа, где он и будет храниться, пока количество наборов опять же не
превысит порога.
Хэш-дерево с
кандидатами-наборами построено, теперь, используя хэш-дерево, легко подсчитать
поддержку для каждого кандидата. Для этого нужно 'пропустить' каждую транзакцию
через дерево и увеличить счетчики для тех кандидатов, чьи элементы также
содержатся и в транзакции, т.е. Ck Ti
= Ck. На корневом уровне хэш-функция применяется к каждому элементу
из транзакции. Далее, на втором уровне, хэш-функция применяется ко вторым
элементам и т.д. На k-уровне хэшируется k-элемент. И так до тех пор, пока не
достигнем листа. Если кандидат, хранящийся в листе, является подмножеством
рассматриваемой транзакции, тогда увеличиваем счетчик поддержки этого кандидата
на единицу.
После того, как каждая
транзакция из исходного набора данных 'пропущена' через дерево, можно проверить
удовлетворяют ли значения поддержки кандидатов минимальному порогу. Кандидаты,
для которых это условие выполняется, переносятся в разряд часто встречающихся.
Кроме того, следует запомнить и поддержку набора, она нам пригодится при
извлечении правил. Эти же действия применяются для нахождения (k+1)-элементных
наборов и т.д. После того как найдены все часто встречающиеся наборы элементов,
можно приступить непосредственно к генерации правил.
Извлечение правил –
менее трудоемкая задача. Во-первых, для подсчета достоверности правила
достаточно знать поддержку самого набора и множества, лежащего в условии
правила. Например, имеется часто встречающийся набор {A, B, C} и требуется
подсчитать достоверность для правила AB C. Поддержка
самого набора нам известна, но и его множество {A, B}, лежащее в условии
правила, также является часто встречающимся в силу свойства анти-монотонности,
и значит его поддержка нам известна. Тогда мы легко сможем подсчитать
достоверность. Это избавляет нас от нежелательного просмотра базы транзакций,
который потребовался в том случае, если бы это поддержка была неизвестна.
Чтобы извлечь правило из
часто встречающегося набора F, следует найти все его непустые подмножества. И
для каждого подмножества s мы сможем сформулировать правило s (F –
s), если достоверность правила conf(s (F –
s)) = supp(F)/supp(s) не меньше порога minconf.
Заметим, что числитель
остается постоянным. Тогда достоверность имеет минимальное значение, если
знаменатель имеет максимальное значение, а это происходит в том случае, когда в
условии правила имеется набор, состоящий из одного элемента. Все супермножества
данного множества имеют меньшую или равную поддержку и, соответственно, большее
значение достоверности. Это свойство может быть использовано при извлечении
правил. Если мы начнем извлекать правила, рассматривая сначала только один
элемент в условии правила, и это правило имеет необходимую поддержку, тогда все
правила, где в условии стоят супермножества этого элемента, также имеют
значение достоверности выше заданного порога. Например, если правило A BCDE
удовлетворяет минимальному порогу достоверности minconf, тогда AB CDE также
удовлетворяет. Для того, чтобы извлечь все правила используется рекурсивная
процедура. Важное замечание: любое правило, составленное из часто
встречающегося набора, должно содержать все элементы набора. Например, если
набор состоит из элементов {A, B, C}, то правило A B не должно
рассматриваться.
2.2 Алгоритм вычисления обобщенных ассоциативных
правил
Как может показаться с первого взгляда, для вычисления
обобщенных ассоциативных правил можно использовать любой алгоритм выявления
ассоциативных правил, дополнив каждую транзакцию предками каждого элемента,
входящего в транзакцию. Однако такой метод 'в лоб' очень неэффективен и
использование его влечет за собой следующие проблемы:
1. Размер каждой транзакции увеличивается в зависимости
от глубины дерева от нескольких десятков процентов до нескольких раз, и как
следствие, увеличение времени вычисления и количества правил.
2. Появление избыточных правил, в которых в условии и в
следствии находятся элемент и его предок. Примером такого правила может быть
'Если покупатель купил Кефир, то он, скорее всего, захочет купить Молочные
продукты'. Совершенно ясно, что практическая ценность этого правила равна нулю
при достоверности равной 100%.
Для решения этой
проблемы может быть использование специального алгоритма, учитывающего всю
специфику обобщенных ассоциативных правил.
Процесс вычисления
обобщенных ассоциативных правил можно разбить на несколько этапов:
1. Поиск часто встречающихся множеств элементов,
поддержка которых больше чем заданный порог поддержки (минимальная поддержка).
2. Вычисления правил на основе найденных на предыдущем
этапе часто встречающихся множеств элементов. Основная идея вычисления правил
на основе часто встречающихся множеств заключается в следующем: Если
ABCD – это часто встречающееся множество элементов, то на основе этого
множества можно построить правила X 
Y (например,
AB CD), причем
X Y = ABCD.
Поддержка правила равна поддержке часто встречающегося множества. Достоверность
правила вычисляется по формуле conf(X Y) = supp(X Y) /
supp(X). Правило добавляется к результирующему списку правил, если
достоверность этого правила больше порога minconf.
3. Из результирующего списка правил удаляются все
'неинтересные' правила.
2.3 Базовый алгоритм поиска часто встречающихся
множеств
На первом шаге алгоритма
подсчитываются 1-элементные часто встречающиеся наборы. При этом элементы могут
находиться на любом уровне таксономии. Для этого необходимо 'пройтись' по всему
набору данных и подсчитать для них поддержку, т.е. сколько раз встречается в
базе.
Следующие шаги будут
состоять из двух частей: генерации потенциально часто встречающихся наборов
элементов (их называют кандидатами) и подсчета поддержки для кандидатов.
Описанный
выше алгоритм можно записать в виде следующего псевдокода:
1. L1 = { Часто встречающиеся множества
элементов и групп элементов };
2. для( k=2; Lk-1 <> 
; k++ )
3. {
4. Ck = { Генерация кандидатов
мощностью k на основе Lk-1 };
5. для всех транзакций t 
D
6. {
7. Расширить
транзакцию t предками всех элементов,
8. входящих
в транзакцию;
9. Удалить
дубликаты из транзакции t;
10. для
всех кандидатов с Ck
11. если
с 
t то
12. c.count++;
13. }
14. Lk = { с Ck
| c.count >= minsupp }; // Отбор кандидатов
15. }
16. Результат = UkLk;
Опишем
функцию генерации кандидатов. Для того чтобы получить k-элементные наборы,
воспользуемся (k-1)-элементными наборами, которые были определены на предыдущем
шаге и являются часто встречающимися.
Алгоритм
генерации кандидатов будет состоять из двух шагов:
1. Объединение. Каждый кандидат Ck будет
формироваться путем расширения часто встречающегося набора размера (k-1)
добавлением элемента из другого (k-1)- элементного набора.Приведем алгоритм
этой функции в виде небольшого SQL-подобного запроса:
INSERT INTO Ck
SELECT a.item1,
a.item2, …, a.itemk-1, b.itemk-1
FROM Fk-1
a, Fk-1 b
WHERE a.item1 = b.item1,
a.item2 = b.item2, … , a.itemk-2 = b.itemk-2,
a.itemk-1 < b.itemk-1
2. Удаление избыточных правил. На основании свойства
анти-монотонности, следует удалить все наборы c Ck, если хотя бы
одно из его (k-1) подмножеств не является часто встречающимся.
Для эффективного подсчета поддержки кандидатов можно
использовать хэш-дерево. Хеш-дерево строится каждый раз, когда формируются
кандидаты. Первоначально дерево состоит только из корня, который является
листом, и не содержит никаких кандидатов-наборов. Каждый раз, когда формируется
новый кандидат, он заносится в корень дерева и так до тех пор, пока количество
кандидатов в корне-листе не превысит некоего порога. Как только количество
кандидатов становится больше порога, корень преобразуется в хеш-таблицу, т.е.
становится внутренним узлом, и для него создаются потомки-листья. И все примеры
распределяются по узлам-потомкам согласно хеш-значениям элементов, входящих в
набор, и т.д. Каждый новый кандидат хешируется на внутренних узлах, пока он не
достигнет первого узла-листа, где он и будет храниться, пока количество наборов
опять же не превысит порога.
2.4 Улучшенный алгоритм поиска часто
встречающихся множеств
К базовому алгоритму можно добавить несколько оптимизаций,
которые увеличат скорость работы базового алгоритма:
1. Целесообразно единожды вычислить множества предков для
каждого элемента иерархии как для элемента нижнего уровня таксономии (лист
дерева), так и для элемента внутреннего уровня.
2. Необходимо удалять кандидаты, содержащие элемент и его
предок. Для реализации этой оптимизации рассмотрим следующие две леммы:
Лемма
1. Поддержка множества X, содержащего
и элемент x и его предок x вычисляется по формуле supp(X)=supp(X-x).Принимая
во внимание эту лемму, мы будем удалять кандидаты, содержащие и элемент и его
предок из списка кандидатов до начала процесса подсчета поддержки.
Лемма
2. Если Lk – это
список часто встречающихся множеств, не содержащий множеств, включающих и
элемент и его предок в одном множестве, то Ck+1 (список кандидатов,
получаемых из Lk) также не будет содержать множеств, включающих и
элемент и его предок.
Учитывая утверждение, данное в этой лемме, мы будем
удалять кандидатов, включающих и элемент и его предок, из списка кандидатов
только на первой итерации внешнего цикла.
3. Нет необходимости в добавлении всех предков всех
элементов, входящих в транзакцию. Если кокой-то элемент, у которого есть
предок, не находится в списке кандидатов, то в списке элементов с предками он
помечается как удаленный. Следовательно, из транзакции удаляются элементы,
помеченные как удаленные, или производится замена этих элементов на их предков.
К транзакции добавляются только не удаленные предки.
4. Не 'пропускать' транзакцию через хэш-дерево, если ее
мощность меньше чем мощность элементов, расположенных в хэш-дереве.
5. Целесообразно помечать транзакции как удаленные и не
использовать их при подсчете поддержки на следующих итерациях, если на текущей
итерации в эту транзакцию не вошел ни один кандидат.
Учитывая
написанное выше, получаем следующий алгоритм:
1. // Оптимизация 1
2. Вычислить I* множества предков элементов для каждого
элемента;
3. L1 = {Часто встречающиеся множества
элементов и групп элементов};
4. для ( k = 2; Lk-1 <> ; k++ )
5. {
6. Ck
= {Генерация кандидатов мощностью k на основе Lk-1};
7. //
Оптимизация 2
8. если k
= 2 то
9. удалить
те кандидаты из Ck, которые содержат элемент и его предок;
10. //
Оптимизация 3
11. Пометить
как удаленные множества предков элемента, который не содержится в списке
кандидатов;
12. для
всех транзакций t D
13. {
14. //
Оптимизация 3
15. для
каждого элемента х t
16. добавить
всех предков х из I* к t;
17. Удалить
дубликаты из транзакции t;
18. //
Оптимизация 4,5
19. если
(t не помечена как удаленная) и ( |t| >= k) то
20. {
21. для
всех кандидатов с Ck
22. если
с t то
23. c.count++;
24. //
Оптимизация 5
25. если
в транзакцию t не вошел ни один кандидат то
26. пометить
эту транзакцию как удаленную;
27. }
28. }
29. //
Отбор кандидатов
30. Lk
= { с >= Ck | c.count
>= minsupp };
31. }
32. Результат = UkLk;
Заключение
В данной работе были рассмотрены ассоциативные правила, как один из инструментов Data
Mining, позволяющие эффективно обрабатывать большие объемы данных
и находить необходимую информацию. Как было сказано,
задача поиска ассоциативных правил впервые была представлена для анализа
рыночной корзины. Ассоциативные правила эффективно используются в сегментации
покупателей по поведению при покупках, анализе предпочтений клиентов,
планировании расположения товаров в супермаркетах, кросс-маркетинге, адресной
рассылке. Однако, сфера применения этих алгоритмов не ограничивается лишь одной
торговлей. Их также успешно применяют и в других областях: медицине, для
анализа посещений веб-страниц (Web Mining), для анализа текста (Text Mining),
для анализа данных по переписи населения, в анализе и прогнозировании сбоев
телекоммуникационного оборудования и т.д.