Помадин С.С. Исследование распределений статистик многомерного анализа данных при нарушении предположений о нормальности // Диссертация на соискание уч. ст. к.т.н. по специальности 05.13.17 — теоретические основы информатики / Научн. рук. д.т.н., проф. Лемешко Б.Ю./ Новосибирский государственный технический университет, 2004 г.
Глава 1. Постановка задач исследования
1.1. Основные понятия и определения
1.2. Задачи корреляционного анализа
1.2.1. Критерии проверки гипотез о векторе математических ожиданий и ковариационной матрице
1.2.2. Критерии проверки гипотез о коэффициентах корреляции
1.2.3. Критерии проверки гипотез о корреляционном отношении
1.4. Проблемы моделирования многомерных псевдослучайных величин
2.1. Классические критерии проверки гипотез о математических ожиданиях и дисперсиях
2.2.
Распределения статистик ![]() ,
,
![]() ,
, ![]() ,
, ![]() при нарушении предположений
о нормальности
при нарушении предположений
о нормальности
3.1.1. Проверка гипотез о векторе математических ожиданий
3.1.2. Проверка гипотез о ковариационной матрице
3.3. Исследование распределений статистик при законах, отличающихся от нормального
3.4. Уточнение моделей распределений статистик рассматриваемых критериев
4. Исследование критериев проверки гипотез о коэффициентах корреляции
4.1. Классические критерии проверки гипотез о коэффициентах корреляции
4.1.1. Проверка гипотез о коэффициентах парной корреляции
4.1.2. Проверка гипотез о коэффициентах частной корреляции
4.1.3. Проверка гипотезы о коэффициенте множественной корреляции
4.2. Исследование распределений статистик критериев для различных многомерных законов
4.2.1. В случае принадлежности наблюдений многомерному нормальному закону
4.2.3. Случай принадлежности наблюдений многомерному закону Стьюдента
5. Исследование критериев проверки гипотез о корреляционном отношении
5.1. Классические критерии проверки гипотез о корреляционном отношении
5.4.
Исследование распределений статистики критерия линейности регрессии ![]() по
по ![]()
Глава 6. Описание программной системы
6.1. Общая характеристика программной системы
6.2. Краткое описание интерфейса программной системы
6.2.2. Вспомогательная программа
6.3. Моделирование псевдослучайных величин.
6.3.1. Моделирование одномерных распределений.
6.3.2. Моделирование псевдослучайных нормальных векторов
6.3.3. Моделирование многомерных величин по законам, отличным от нормального
6.3.5.
Моделирование функциональной линейной зависимости между ![]() и
и ![]()
6.4. Пример использования программной системы при обработке данных в медицине
Список использованных источников
Введение
Современное состояние и актуальность темы исследований. Существует множество работ по многомерному статистическому анализу [13, 31, 36, 44, 45, 47, 94, 95, 108, 114], содержание которых указывает на актуальность и эффективность применения соответствующего математического аппарата в различных областях знаний, таких как экономика, биология и медицина. При этом в практике статистического анализа возникает существенно больше постановок задач, чем предлагается решений в классической математической статистике [101]. Разнообразие статистических гипотез, выдвигаемых в процессе статистического анализа в различных приложениях, оказывается существенно шире предлагаемого классическим аппаратом. Классический аппарат включает в себя ограниченный перечень задач проверки статистических гипотез, для которых найдены предельные распределения статистик, используемых в соответствующих критериях. Поэтому классические результаты оказываются применимыми при выполнении достаточно строгих предположений, которые на практике часто не имеют места.
С другой стороны, для обнаружения закономерных связей можно использовать аппарат анализа данных [53,54,63,64], когда рассматриваемые объекты представляются как <<черные ящики>>. В данном случае на анализируемые данные не накладываются какие"– либо строгие ограничения. Но применение такого подхода обычно привязано к определенному классу задач, например, распознавание образов, и поэтому далеко не всегда удается использовать методы анализа данных в растущем множестве различных статистических задач.
Таким образом, можно говорить о наличии в математической статистике множества <<пробелов>>, которые чаще всего связаны с проверкой разного рода статистических гипотез. В этом случае вопрос обычно упирается в необходимость нахождения предельного распределения статистики построенного критерия или распределения статистики при заданном объеме выборки. Как правило, нахождение предельного закона для статистики критерия проверки конкретной гипотезы аналитическими методами оказывается чрезвычайно сложной задачей, а задач, требующих разрешения, "— слишком много [124].
В большинстве случаев отсутствие необходимых теоретических результатов объясняется сложностью и трудоемкостью получения решений аналитическими методами. Можно констатировать, что количество и уровень сложности задач, выдвигаемых практикой, возрастают настолько быстро, что ресурсы человеческого интеллекта, его производительность просто не в состоянии обеспечить решение такого множества задач без создания и использования соответствующих вычислительных технологий.
Сегодня в связи с бурным развитием и внедрением персональных компьютеров, особую актуальность приобретает задача обеспечения высокого качества пакетов прикладных статистических программ. Несмотря на то, что, рынок насыщен различными пакетами программных систем статистического анализа[22,115], реализуемые в них методы и алгоритмы сильно отстают от последних достижений в области статистических исследований. С одной стороны это объясняется, прежде всего, тем, что подробное описание последних результатов исследований очень сложно отыскать в литературных источниках, поэтому они остаются труднодоступными для разработчиков программного обеспечения. К сожалению, с другой стороны необходимо отметить и то, что в некоторых работах встречаются ошибки применения статистических методов [98], что также не облегчает быстрое внедрение новых методов в программные пакеты.
Перспективы программного обеспечения по статистическому анализу данных обсуждались в работах [27-30,38], современные проблемы внедрения прикладной статистики поднимались в [100]. Расширяющиеся использование ЭВМ и их совершенствование в свою очередь отражается на развитии статистических методов и использовании статистических методов в приложениях [14, 32, 35, 42, 48, 56, 65, 104, 109, 116, 120].
Вышесказанное подчеркивает необходимость (а практика уже показывает возможность [61,67,81,82,86,89,90]) развития компьютерных методов исследования статистических закономерностей, компьютерных методов исследования свойств оценок и статистик различных критериев проверки статистических гипотез, построения вероятностных моделей для исследуемых закономерностей. Это позволяет с меньшими интеллектуальными затратами получать фундаментальные знания в области математической статистики, и, следовательно, осуществлять корректные статистические выводы при анализе данных в различных прикладных областях.
В последние годы при исследовании некоторых задач математической и прикладной статистики получено множество результатов, связанных с исследованием распределений статистик критериев согласия в случае проверки простых и сложных гипотез [84,86-88], с исследованием статистических свойств различных оценок [69,91], полученных как раз благодаря применению методов компьютерного моделирования. Накопленный опыт в данной области показал, что с использованием методов статистического моделирования и последующего анализа можно получать результаты по точности не уступающие аналитическим. Например, при оценивании параметров распределений некоторых законов в случаях проверки сложных гипотез с использованием методов статистического моделирования, когда наиболее часто применяют метод Монте"– Карло [37, 49, 51, 52, 113], были получены таблицы процентных точек для предельных распределений статистик непараметрических критериев [5, 17, 23, 24, 117–119, 121]. В этой связи появилась обоснованная уверенность, что с использованием данного подхода можно закрывать многие существующие в прикладной статистике <<пробелы>>, применяя относительно простой вычислительный и математический аппарат.
В различных приложениях статистического анализа многомерных случайных величин одну из ключевых позиций занимают задачи корреляционного анализа [122]. В процессе решения задач корреляционного анализа выявляется наличие и характер взаимосвязи величин, взаимозависимости величин при устранении влияния совокупности других или зависимости одной случайной величины от группы величин. Вычисляются оценки коэффициентов и матриц парной, частной и множественной корреляции, проверяются различные статистические гипотезы относительно параметров многомерного распределения и коэффициентов корреляции. На основании результатов корреляционного анализа может делаться вывод о наличии и характере функциональной зависимости или предпочтительности для описания исследуемого объекта регрессионной модели того или иного вида.
В основе существующего аппарата корреляционного анализа лежит предположение о принадлежности наблюдаемого случайного вектора многомерному нормальному закону. Базируясь на этом, получены предельные распределения статистик, используемых в критериях многомерного анализа [2, 16, 33, 57–59].
На практике, исследователь далеко не всегда имеет дело с нормальным законом [16,94,99]. Как правило, многие исследователи вообще не придают значения проверке этого важного предположения корреляционного анализа, либо они вынуждены <<в силу обстоятельств>> работать только с многомерными величинами, имеющим нормальное распределение, как это сделано в работах [31,114]. Например, в нашей жизни достаточно мало экономических процессов, отклонения которых распределены по нормальному закону. Поэтому данное ограничение приводит к сужению области применения корреляционного анализа в экономике. Естественно, возникает вопрос о справедливости выводов, получаемых на основании результатов корреляционного анализа при нарушении основного предположения. В доступной литературе ответ на данный вопрос найден не был, хотя можно найти указания на робастность некоторых критериев, применяемых в многомерном анализе.
Целью данной диссертационной работы явилось стремление разобраться, что будет происходить с распределениями различных статистик корреляционного анализа, если наблюдаемый закон будет отличаться от многомерного нормального.
Немаловажен и такой аспект. Большинство наиболее весомых результатов
в математической статистике имеет асимптотический характер. На практике же
всегда имеют дело с ограниченными объемами наблюдений. И свойства используемых
статистик в таких ситуациях порой существенно отличаются от асимптотических. Не
являются исключением и предельные распределения статистик корреляционного
анализа, которые получены для выборок многомерных величин с объемом ![]() [2, 33, 57,
58]. На практике исследователю важно знать конечные объемы выборок, начиная с
которых можно пользоваться найденными предельными законами. Поэтому в процессе
проводимых исследований можно оценить объемы выборок, которые могут быть
рекомендованы как достаточные для принятия правильного решения по соответствующему
критерию корреляционного анализа.
[2, 33, 57,
58]. На практике исследователю важно знать конечные объемы выборок, начиная с
которых можно пользоваться найденными предельными законами. Поэтому в процессе
проводимых исследований можно оценить объемы выборок, которые могут быть
рекомендованы как достаточные для принятия правильного решения по соответствующему
критерию корреляционного анализа.
Очевидно, что ответить на поставленные вопросы, используя аналитические методы, чрезвычайно сложно из-за нетривиальности возникающих задач. Поэтому в основу проводимого исследования положена развиваемая на кафедре прикладной математики НГТУ методика компьютерного моделирования и анализа статистических закономерностей.
Цели и задачи исследований. Основной целью диссертационной работы является исследование поведения (предельных) законов распределений статистик многомерного анализа в случае принадлежности наблюдаемых случайных величин многомерным законам распределения, отличным от нормального.
Для достижения поставленной цели было предусмотрено решение следующих задач:
· исследование эмпирических распределений статистик корреляционного анализа в случае многомерного нормального закона для подтверждения теоретических результатов и выявления скорости сходимости распределений к соответствующим предельным;
· моделирование многомерных законов, отличных от нормального, с заданными вектором математических ожиданий, ковариационной матрицей и задаваемой мерой отклонения от нормального;
· исследование распределений статистик, используемых при проверке гипотез о векторе математических ожиданий и ковариационной матрице, в случае многомерных законов, отличающихся от нормального;
· исследование распределений статистик, используемых при проверке гипотез о парном, частном и множественном коэффициентах корреляции, в случае многомерных законов, отличающихся от нормального;
· исследование влияния способов группирования и количества интервалов на оценку корреляционного отношения, исследование критериев, используемых при проверке гипотез о корреляционном отношении;
· исследование критериев проверки гипотез о математическом ожидании и дисперсии в одномерном случае при наблюдениях, не подчиняющихся нормальному закону.
Методы исследования. Для решения поставленных задач использовался аппарат теории вероятностей, математической статистики, вычислительной математики, математического программирования, статистического моделирования.
Научная новизна диссертационной работы заключается в:
· результатах исследования распределений статистик многомерного анализа данных при нарушении предположений о нормальном законе многомерных случайных величин;
· результатах исследования распределений статистик критериев, используемых при проверке гипотез о математическом ожидании и дисперсии, в случае принадлежности наблюдений семейству симметричных распределений;
· методе моделирования многомерных случайных величин по законам, заданным образом отличающихся от нормального.
Основные положения, выносимые на защиту.
Результаты исследования сходимости распределений статистик многомерного анализа к предельным распределениям в зависимости от объема выборки при наблюдаемом нормальном законе случайных векторов.
Подход и алгоритм моделирования многомерного закона распределения, отличающегося от нормального, с заданными вектором математических ожиданий и ковариационной матрицей.
Результаты исследований распределений статистик многомерного анализа для ситуаций, когда наблюдаемый многомерный закон отличается от нормального.
Результаты исследований распределений статистик критериев, используемых для проверки гипотез о математическом ожидании и дисперсии.
Практическая ценность и реализация результатов. Результаты исследования распределений статистик классического корреляционного анализа позволяют существенно расширить сферу корректного применения ряда критериев на многомерные законы, в достаточно широких пределах отличающиеся от нормального (более островершинных или более плосковершинных). Для законов такого вида показано, что распределения статистик, используемых в критериях проверки гипотез о векторе математических ожиданий и о нулевых значениях парного, частного и множественного коэффициентов корреляции, по–прежнему хорошо описываются классическими предельными распределениями. В случае других исследуемых критериев выявлена явная зависимость от наблюдаемого многомерного закона. Предложен метод моделирования многомерных случайных векторов с задаваемым параметром отклонения от многомерного нормального закона.
Апробация работы. Основные результаты исследований докладывались на Новосибирской межвузовской НТК <<Интеллектуальный потенциал Сибири>> (Новосибирск, 2000); Российской НТК <<Информатика и проблемы телекоммуникаций>> (Новосибирск, 2000, 2001, 2002, 2003, 2004); V международной конференции <<Актуальные проблемы электронного приборостроения АПЭП-2000>> (Новосибирск, 2000); Региональной НТК студентов, аспирантов, молодых ученых <<Наука. Техника. Инновации>> (Новосибирск, 2001); Всероссийской НТК <<Информационные системы и технологии ИСТ-2001>> (Нижний Новгород, 2001); VI международной конференции <<Актуальные проблемы электронного приборостроения АПЭП-2002>> (Новосибирск, 2002); Региональной конференции <<Вероятностные идеи в науке и философии>> (Новосибирск, 2003); всероссийской НТК <<Информационные системы и технологии ИСТ-2004>> (Нижний Новгород, 2004). Исследования по теме диссертации были поддержаны грантом Минобразования РФ (проект A03-2.8-280), вошли составной частью в работы, поддержанные Российским фондом фундаментальных исследований (проект 00-01-00913) и грантом Минобразования РФ (проект T02-3.3-3356).
Публикации. По теме диссертации опубликовано 16 печатных работ. Среди которых 8 публикаций отражают основные результаты исследований.
Структура работы. Диссертация состоит из введения, 6 глав основного содержания, включая 11 таблиц и 48 рисунков, заключения, списка использованных источников и приложения.
Краткое содержание работы. В первой главе представлен обзор проблем, связанных с встречающимися на практике многомерными наблюдениями, не подчиняющимися нормальному закону, и, как следствие, неприменимости ряда критериев многомерного анализа данных. Даются основные определения и теоремы, на которых базируется классический аппарат корреляционного анализа.
Во второй главе исследуются распределения классических статистик, используемых в критериях проверки гипотез о математических ожиданиях и дисперсиях, если наблюдаемый закон в той или иной мере отличается от нормального.
В третьей главе исследуются распределения статистик критериев, используемых при проверке гипотез о векторе математических ожиданий и ковариационной матрице, в случае многомерных законов, отличных от нормального.
В четвертой главе приводятся результаты исследования распределений статистик, применяемых в критериях проверки гипотез о парном, частном и множественном коэффициентах корреляции.
В пятой главе рассматриваются проблемы, связанные с вычислением оценки корреляционного отношения и влиянием различных способов группирования на получаемую оценку, исследуются критерии проверки гипотез о корреляционном отношении.
В шестой главе дано краткое описание исследовательской программной системы и предлагается метод моделирования многомерных случайных величин с заданным <<отклонением>> от многомерного нормального закона. Показывается различие между моделируемым и многомерным нормальным законами.
Глава 1. Постановка задач исследования
1.1. Основные понятия и определения
Введем для дальнейшего использования следующие обозначения:
![]() —
выборка из
—
выборка из ![]() наблюдений
наблюдений
![]() -мерного
случайного вектора;
-мерного
случайного вектора;
![]() —
математическое ожидание случайного вектора
—
математическое ожидание случайного вектора ![]() ;
;
![]() —
ковариационная матрица случайного вектора
—
ковариационная матрица случайного вектора ![]() ;
;
![]() —
парный коэффициент корреляции между компонентами
—
парный коэффициент корреляции между компонентами ![]() и
и ![]() случайного вектора
случайного вектора ![]() ;
;
![]() —
частный коэффициент корреляции между компонентами
—
частный коэффициент корреляции между компонентами ![]() и
и ![]() случайного вектора
случайного вектора ![]() при исключении
влияния компонент
при исключении
влияния компонент ![]() ;
;
![]() —
множественный коэффициент корреляции между
—
множественный коэффициент корреляции между ![]() и множеством компонент
и множеством компонент ![]() случайного
вектора
случайного
вектора ![]() ;
;
![]() —
корреляционное отношение компоненты
—
корреляционное отношение компоненты ![]() по
по ![]() случайного вектора
случайного вектора ![]() ;
;
![]() и
и ![]() — несмещенные
оценки максимального правдоподобия (ОМП) математического ожидания и
ковариационной матрицы, которые вычисляются по следующим формулам
— несмещенные
оценки максимального правдоподобия (ОМП) математического ожидания и
ковариационной матрицы, которые вычисляются по следующим формулам
![]()
![]() ,
, ![]() ,
, ![]() и
и ![]() — ОМП соответствующих
величин, вычисляемых по формулам (4.1), (4.5), (4.8) и (5.2).
— ОМП соответствующих
величин, вычисляемых по формулам (4.1), (4.5), (4.8) и (5.2).
![]() (4.1)
(4.1)
Представим случайный вектор ![]() в следующем виде [33]:
в следующем виде [33]:
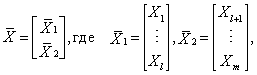
а вектор математических ожиданий и ковариационную матрицу соответственно в виде
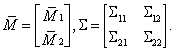
Тогда если случайный вектор ![]() подчиняется нормальному закону с
вектором средних
подчиняется нормальному закону с
вектором средних ![]() и ковариационной матрицей
и ковариационной матрицей ![]() , то условное
распределение подвектора
, то условное
распределение подвектора ![]() при известном
при известном ![]() является нормальным с
математическим ожиданием
является нормальным с
математическим ожиданием ![]() и ковариационной матрицей
и ковариационной матрицей ![]() , где
, где ![]() ,
, ![]() [58].
[58].
ОМП для частного коэффициента корреляции определяется соотношением:
![]() (4.5)
(4.5)
где ![]() —
элемент
—
элемент ![]() -й
строки и
-й
строки и ![]() -го
столбца матрицы
-го
столбца матрицы ![]() ,
, ![]() — число компонент в условном
распределении,
— число компонент в условном
распределении, ![]() .
В данном случае при оценке взаимозависимости между компонентами
.
В данном случае при оценке взаимозависимости между компонентами ![]() и
и ![]() случайной
величины
случайной
величины ![]() исключается
влияние компонент
исключается
влияние компонент ![]() .
.
С учетом выше рассмотренного разбиения случайного вектора ![]() ОМП множественного
коэффициента корреляции между
ОМП множественного
коэффициента корреляции между ![]() и множеством компонент
и множеством компонент ![]() определяется
соотношением
определяется
соотношением
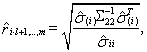 (4.8)
(4.8)
где ![]() —
i-ая строка матрицы
—
i-ая строка матрицы ![]() ,
, ![]() — элемент матрицы
— элемент матрицы ![]() .
.
Корреляционное отношение случайной величины ![]() по
по ![]() определяется отношением
дисперсии условного математического ожидания
определяется отношением
дисперсии условного математического ожидания ![]() к дисперсии
к дисперсии ![]() :
:
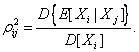 (5.1)
(5.1)
В отличие от коэффициента корреляции ![]() корреляционное отношение
корреляционное отношение ![]() несимметрично
относительно
несимметрично
относительно ![]() и
и
![]() .
Соотношение между коэффициентом корреляции
.
Соотношение между коэффициентом корреляции ![]() и корреляционным отношением
и корреляционным отношением ![]() в случае
многомерного нормального закона позволяет утверждать следующее[58]:
в случае
многомерного нормального закона позволяет утверждать следующее[58]:
·
![]() ,
если
,
если ![]() и
и
![]() независимы;
независимы;
·
![]() ,
тогда и только тогда, когда имеется строгая линейная функциональная зависимость
,
тогда и только тогда, когда имеется строгая линейная функциональная зависимость
![]() от
от ![]() ;
;
·
![]() ,
тогда и только тогда, когда имеется строгая нелинейная функциональная
зависимость
,
тогда и только тогда, когда имеется строгая нелинейная функциональная
зависимость ![]() от
от
![]() ;
;
·
![]() ,
тогда и только тогда, когда регрессия
,
тогда и только тогда, когда регрессия ![]() по
по ![]() строго линейная, но нет
функциональной зависимости;
строго линейная, но нет
функциональной зависимости;
·
![]() ,
указывает на то, что не существует функциональной зависимости, и некоторая
нелинейная кривая регрессии <<подходит>> лучше, чем <<наилучшая>>
прямая линия.
,
указывает на то, что не существует функциональной зависимости, и некоторая
нелинейная кривая регрессии <<подходит>> лучше, чем <<наилучшая>>
прямая линия.
Таким образом, равенство квадрата коэффициента корреляции корреляционному отношению указывает на то, что для регрессии нельзя найти лучшей кривой, чем прямая линия.
Оценка корреляционного отношения определяется выражением
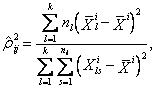 (5.2)
(5.2)
где ![]() —
количество интервалов сечений для компоненты
—
количество интервалов сечений для компоненты ![]() ;
; ![]() — среднее значение компоненты
— среднее значение компоненты ![]() в
в ![]() – ом
сечении;
– ом
сечении; ![]() —
число наблюдений компоненты
—
число наблюдений компоненты ![]() в
в ![]() – ом сечении;
– ом сечении; ![]() — значение компоненты
— значение компоненты
![]() с
номером
с
номером ![]() в
в ![]() – ом
сечении.
– ом
сечении.
1.2. Задачи корреляционного анализа
1.2.1. Критерии проверки гипотез о векторе математических ожиданий и ковариационной матрице
Важными статистическими задачами корреляционного анализа являются
задачи проверки гипотез о том, что вектор математических ожиданий нормального
распределения является данным вектором. Эти задачи могут быть рассмотрены в предположении,
что ковариационная матрица ![]() известна из ранее проводимых
экспериментов, или неизвестна, тогда она должна быть оценена.
известна из ранее проводимых
экспериментов, или неизвестна, тогда она должна быть оценена.
Критерии для проверки гипотез о векторе математических ожиданий, основываются на следующих двух теоремах [2-4,18,19,25,33,59].
Теорема 1. Если проверяемая гипотеза для выборки объема ![]() , взятой из
совокупности с нормальным законом
, взятой из
совокупности с нормальным законом ![]() , имеет вид
, имеет вид ![]() и ковариационная матрица
и ковариационная матрица ![]() известна, тогда
гипотеза
известна, тогда
гипотеза ![]() не
отклоняется с уровнем значимости
не
отклоняется с уровнем значимости ![]() при выполнении неравенства
при выполнении неравенства
![]() (1.1)
(1.1)
где распределение ![]() левой части неравенства есть
левой части неравенства есть ![]() "– распределение
с
"– распределение
с ![]() степенями
свободы, и
степенями
свободы, и ![]() удовлетворяет
равенству
удовлетворяет
равенству
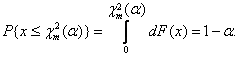 (1.2)
(1.2)
Теорема 2. Когда ковариационная матрица ![]() неизвестна и проверяется
гипотеза
неизвестна и проверяется
гипотеза ![]() по
выборке
по
выборке ![]() "– мерного
случайного вектора объема
"– мерного
случайного вектора объема ![]() , полученной из совокупности с
нормальным законом
, полученной из совокупности с
нормальным законом ![]() , то гипотеза
, то гипотеза ![]() не отвергается для уровня
значимости
не отвергается для уровня
значимости ![]() ,
если
,
если
![]() (1.3)
(1.3)
где распределение ![]() левой части неравенства есть
левой части неравенства есть ![]() "– распределение
Фишера с
"– распределение
Фишера с ![]() и
и
![]() степенями
свободы, и
степенями
свободы, и ![]() удовлетворяет
равенству
удовлетворяет
равенству
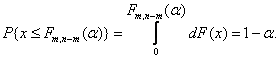 (1.4)
(1.4)
Задачи проверки гипотез о ковариационной матрице имеют вид ![]() , где
, где ![]() "—
номинальное значение ковариационной матрицы. Подразумевается, что вектор математических
ожиданий будет оцениваться по исследуемой выборке. В случае, когда проверяется
совместная гипотеза о векторе математических ожиданий и о ковариационной матрице,
тогда гипотеза имеет вид
"—
номинальное значение ковариационной матрицы. Подразумевается, что вектор математических
ожиданий будет оцениваться по исследуемой выборке. В случае, когда проверяется
совместная гипотеза о векторе математических ожиданий и о ковариационной матрице,
тогда гипотеза имеет вид ![]() . В корреляционном анализе для задач
о ковариационных матрицах используют критерии, определяемые следующими теоремами [2,11,33].
. В корреляционном анализе для задач
о ковариационных матрицах используют критерии, определяемые следующими теоремами [2,11,33].
Теорема 3. Если проверяемая гипотеза имеет вид ![]() для
для ![]() "– мерных
случайных векторов
"– мерных
случайных векторов ![]() , подчиняющихся нормальному закону
, подчиняющихся нормальному закону ![]() , тогда отношение
правдоподобия имеет вид
, тогда отношение
правдоподобия имеет вид
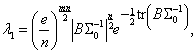 (1.5)
(1.5)
где
![]() (1.6)
(1.6)
В этом случае распределение ![]() статистики
статистики ![]() представляет собой
представляет собой ![]() "– распределение
с
"– распределение
с ![]() степенями
свободы. Гипотеза
степенями
свободы. Гипотеза ![]() принимается с уровнем значимости
принимается с уровнем значимости ![]() , когда выполняется
условие
, когда выполняется
условие
![]() (1.7)
(1.7)
где ![]() удовлетворяет
равенству
удовлетворяет
равенству
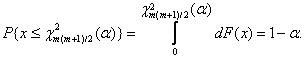 (1.8)
(1.8)
Теорема 4. Для проверки гипотезы ![]() по выборке
по выборке ![]() "– мерных
случайных векторов
"– мерных
случайных векторов ![]() , принадлежащих нормальному закону
, принадлежащих нормальному закону ![]() , отношение правдоподобия
имеет вид
, отношение правдоподобия
имеет вид
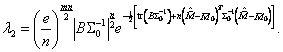 (1.9)
(1.9)
В этом случае распределение ![]() статистики
статистики ![]() представляет собой
представляет собой ![]() "– распределение
с
"– распределение
с ![]() степенями
свободы. Гипотеза
степенями
свободы. Гипотеза ![]() не отвергается при уровне
значимости
не отвергается при уровне
значимости ![]() ,
если
,
если
![]() (1.10)
(1.10)
где ![]() определяется
равенством
определяется
равенством
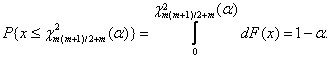 (1.11)
(1.11)
1.2.2. Критерии проверки гипотез о коэффициентах корреляции
В случае необходимости исследования взаимозависимости случайных величин применяют различные критерии корреляционного анализа, предназначенные для выявления характера статистической зависимости. В данной работе затрагиваются задачи корреляционного анализа, связанные с парной, частной и множественной корреляцией случайных величин.
Если требуется исследовать взаимозависимость двух величин, применяют критерии о парной корреляции, которые базируются на следующих теоремах [2,10,12,33,57,58].
Теорема 5. Пусть ![]() "— независимые одинаково
распределенные случайные величины с нормальным законом распределения
"— независимые одинаково
распределенные случайные величины с нормальным законом распределения ![]() . Если
проверяемая гипотеза имеет вид
. Если
проверяемая гипотеза имеет вид ![]() , тогда гипотеза
, тогда гипотеза ![]() не отвергается с уровнем
значимости
не отвергается с уровнем
значимости ![]() при
условии, что выполняется неравенство
при
условии, что выполняется неравенство
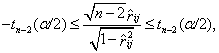 (1.12)
(1.12)
где ![]() "—
ОМП парного коэффициента корреляции между компонентами вектора
"—
ОМП парного коэффициента корреляции между компонентами вектора ![]() и
и ![]() , распределение
, распределение ![]() статистики
статистики ![]() есть
есть ![]() "– распределение
Стьюдента с числом степеней свободы
"– распределение
Стьюдента с числом степеней свободы ![]() , и
, и ![]() удовлетворяет равенству
удовлетворяет равенству
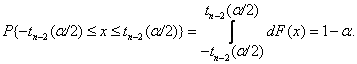 (1.13)
(1.13)
Теорема 6. Если проверяется гипотеза ![]() по выборке
по выборке ![]() случайных
векторов, распределенных по нормальному закону
случайных
векторов, распределенных по нормальному закону ![]() , то гипотеза
, то гипотеза ![]() принимается с уровнем
значимости
принимается с уровнем
значимости ![]() ,
если выполняется соотношение
,
если выполняется соотношение
![]() (1.14)
(1.14)
где 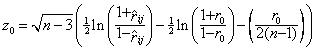 ,
, ![]() "— ОМП парного коэффициента
корреляции между компонентами вектора
"— ОМП парного коэффициента
корреляции между компонентами вектора ![]() и
и ![]() , распределение
, распределение ![]() статистики
статистики ![]() есть стандартное
нормальное распределение, и
есть стандартное
нормальное распределение, и ![]() удовлетворяет
удовлетворяет
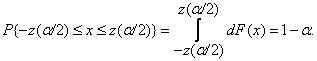 (1.15)
(1.15)
Если нас интересует взаимозависимость двух величин при устранении
воздействия остальных величин, то исследуется, так называемая, частная
корреляция. Критерии проверки гипотез о частном коэффициенте корреляции вида ![]() и
и ![]() базируются на
тех же самых теоремах[2,8,33,58], что и для парного коэффициента корреляции.
Только в этом случае в соответствующих соотношениях
базируются на
тех же самых теоремах[2,8,33,58], что и для парного коэффициента корреляции.
Только в этом случае в соответствующих соотношениях ![]() заменяется на
заменяется на ![]() , где
, где ![]() "— число
компонент случайного вектора в условном распределении
"— число
компонент случайного вектора в условном распределении ![]() и
и ![]() при фиксировании
остальных.
при фиксировании
остальных.
Когда исследуется зависимость единственной величины от группы других, рассматривается множественная корреляция, и используют критерии проверки гипотез о множественной корреляции. В работе рассматривается критерий проверки гипотезы о значимости множественного коэффициента корреляции, базирующийся на следующей теореме [2,9,33,58].
Теорема 7. Если проверяется гипотеза вида ![]() по выборке
по выборке ![]() "– мерного
случайного вектора объема
"– мерного
случайного вектора объема ![]() , полученной из совокупности с
нормальным законом, тогда гипотеза
, полученной из совокупности с
нормальным законом, тогда гипотеза ![]() принимается с уровнем значимости
принимается с уровнем значимости ![]() , если
справедливо следующее неравенство
, если
справедливо следующее неравенство
![]() (1.16)
(1.16)
где ![]() "—
ОМП множественного коэффициента корреляции. Распределение
"—
ОМП множественного коэффициента корреляции. Распределение ![]() левой части неравенства
представляет собой
левой части неравенства
представляет собой ![]() "– распределение Фишера с
"– распределение Фишера с ![]() и
и ![]() степенями
свободы,
степенями
свободы, ![]() удовлетворяет
равенству
удовлетворяет
равенству
 (1.17)
(1.17)
1.2.3. Критерии проверки гипотез о корреляционном отношении
В корреляционном анализе на основании соотношений между парным коэффициентом корреляции и корреляционным отношением можно судить о характере зависимости между компонентами случайного вектора.
Если требуется проверить гипотезы вида: о равенстве корреляционного
отношения нулю ![]() или
о равенстве корреляционного отношения квадрату коэффициента корреляции
или
о равенстве корреляционного отношения квадрату коэффициента корреляции ![]() (критерий
линейности регрессии
(критерий
линейности регрессии ![]() по
по ![]() ), применяют критерии о
корреляционном отношении, которые базируются на следующих теоремах[58].
), применяют критерии о
корреляционном отношении, которые базируются на следующих теоремах[58].
Теорема 8. Если проверяется гипотеза вида ![]() по выборке
по выборке ![]() "– мерного
случайного вектора объема
"– мерного
случайного вектора объема ![]() , полученной из совокупности с
нормальным законом, тогда гипотеза
, полученной из совокупности с
нормальным законом, тогда гипотеза ![]() принимается с уровнем значимости
принимается с уровнем значимости ![]() , если
справедливо следующее неравенство
, если
справедливо следующее неравенство
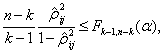 (1.18)
(1.18)
где ![]() "—
оценка корреляционного отношения. Распределение
"—
оценка корреляционного отношения. Распределение ![]() левой части неравенства представляет
собой
левой части неравенства представляет
собой ![]() "– распределение
Фишера с
"– распределение
Фишера с ![]() и
и
![]() степенями
свободы,
степенями
свободы, ![]() удовлетворяет
равенству
удовлетворяет
равенству
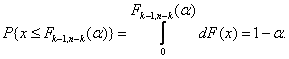 (1.19)
(1.19)
Теорема 9. В случае, когда проверяется гипотеза вида ![]() по выборке
по выборке ![]() случайных
векторов, распределенных по нормальному закону
случайных
векторов, распределенных по нормальному закону ![]() , то гипотеза
, то гипотеза ![]() принимается с уровнем
значимости
принимается с уровнем
значимости ![]() ,
если справедливо следующее неравенство
,
если справедливо следующее неравенство
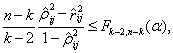 (1.20)
(1.20)
где ![]() и
и
![]() "—
соответственно оценка корреляционного отношения и ОМП парного коэффициента
корреляции. Распределение
"—
соответственно оценка корреляционного отношения и ОМП парного коэффициента
корреляции. Распределение ![]() левой части неравенства
представляет собой
левой части неравенства
представляет собой ![]() "– распределение Фишера с
"– распределение Фишера с ![]() и
и ![]() степенями
свободы,
степенями
свободы, ![]() удовлетворяет
равенству
удовлетворяет
равенству
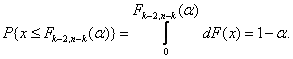 (1.21)
(1.21)
Из приведенных теорем видно, что рассмотренные критерии и распределения статистик получены в предположении о нормальном законе наблюдаемого случайного вектора.
1.3. Цели исследования распределений статистик корреляционного анализа при нарушении предположения о нормальности
Как уже отмечалось, в основе аппарата классического корреляционного анализа лежит предположение о принадлежности наблюдаемого случайного вектора многомерному нормальному закону. Базируясь на этом, сформулированы теоремы о распределениях статистик, используемых в критериях классического корреляционного анализа.
На практике предпосылки классического корреляционного анализа выполняются далеко не всегда. Очевидно и то, что многомерный нормальный закон далеко не всегда является наилучшей моделью для описания реально наблюдаемых многомерных случайных величин [99]. Например, в работе [94] Леонов В. П. отмечает, что за последние 10 лет ему довелось провести достаточно детальный статистический анализ более 150 массивов данных из различных областей экспериментальной биологии и медицины, содержавших от 10 до 300 признаков и от 100 до нескольких десятков тысяч наблюдений. Получилось, что в 50-80% случаев количественные показатели биологических объектов не подчинялись нормальному распределению.
Поэтому центральное место нормального закона не стоит объяснять его универсальной применимостью. Нормальный закон "— это один из многих типов распределения, правда, имеющий основание с относительно большим удельным весом для применения на практике. Его основная привлекательность "— это полнота теоретических исследований. В своих работах [93,94] Леонов В. П. призывает специалистов в биомедицине уделять больше внимания проверке выборок наблюдений на нормальность. Так, проанализированные им работы указывают на то, что некоторые авторы <<забывают>> об осуществлении соответствующих проверок, и впоследствии интерпретируют результаты некорректного применения классических критериев.
Что делать в случае, когда исследователь сталкивается с многомерным законом, который не является нормальным? Как использовать критерии корреляционного анализа? Или какой вид анализа применять в таком случае? Например, в работе [31] Айвазян С. А. предлагает два подхода для исследований наблюдений, которые не подчиняются многомерному нормальному закону. Первый подход заключается в использовании классических алгоритмов для получения первого начального приближения, а второй "— в подборе такого преобразования, которое осуществило бы переход к многомерному нормальному закону. Оба способа очень тяжело реализуются в общем случае, да и исследователь должен быть весьма подготовлен в области статистического анализа, чтобы корректно видоизменять и интерпретировать наблюдаемые величины.
Поэтому с практической точки зрения интересен вопрос о степени корректности выводов, формируемых на основании применения конкретных процедур классического корреляционного анализа, в случае нарушения основного предположения. Насколько корректны будут выводы статистического анализа, если истинная модель многомерного закона в той или иной мере отличается от нормального, и как такое отличие влияет на распределения исследуемых статистик?
Настоятельная потребность в исследовании некоторых критериев корреляционного анализа на устойчивость или, наоборот, неустойчивость к отклонению многомерного закона от нормального проявилась давно. Например, А. Гейен [58] рассмотрел устойчивость коэффициента корреляции к отклонениям от двумерного нормального закона. Им было показано что, когда коэффициент корреляции равен нулю и, в частности, когда случайные величины независимы, критерий проверки гипотезы о нулевом значении коэффициента корреляции устойчив. Но при больших значениях этого коэффициента отклонения от нормальной теории становятся заметными.
В данной работе при помощи методов компьютерного моделирования и анализа закономерностей мы попытались определить границы применимости классического корреляционного анализа, ответить на вопрос, какие критерии можно уверенно применять при отклонении многомерной выборки от нормального закона, а применение каких критериев требует строгого выполнения всех налагаемых условий.
Для подтверждения работоспособности методов компьютерного моделирования и исследования статистических закономерностей в случае многомерных величин в работе исследованы эмпирические распределения статистик классического корреляционного анализа в случае многомерного нормального закона. Эти исследования должны были подтвердить классические результаты и показать близость получаемых эмпирических распределений статистик, в данном случае, известным предельным законам. Соответствие в такой ситуации эмпирических распределений, получаемых в процессе моделирования, предельным классическим распределениям статистик должно послужить доводом, подчеркивающим достоверность результатов в общем случае.
1.4. Проблемы моделирования многомерных псевдослучайных величин
Ключевым моментом для исследования распределений статистик корреляционного анализа при некоторых произвольных многомерных законах (отличающихся от нормального) является необходимость моделирования псевдослучайных векторов в соответствии с такими законами. Причем желательно иметь возможность моделирования псевдослучайных векторов по законам с <<регулируемым удалением>> от многомерного нормального, чтобы проследить соответствующие изменения распределений исследуемых статистик корреляционного анализа.
Алгоритмы моделирования случайных векторов в случае нормального закона, а также для некоторых других частных случаев известны давно [51,52,106]. Эти алгоритмы позволяют достаточно быстро получать выборки случайных векторов произвольных объемов и при различных задаваемых параметрах: векторе математических ожиданий и ковариационной матрице.
Однако моделирование случайных векторов с произвольным распределением до сих пор остается нерешенной проблемой, так как реализация известных общих подходов для решения этой задачи обычно приводит либо к непреодолимым практическим трудностям [51], либо огромным вычислительным затратам для получения больших объемов выборок, например, при использовании метода исключений.
Поэтому возникает потребность в разработке процедуры моделирования многомерных величин, распределенных по законам, отличным от нормального, с заданными математическим ожиданием и ковариационной матрицей, а для задач исследования критериев корреляционного анализа еще и с некоторой заданной мерой близости к многомерному нормальному закону.
В работе [60] Кирьяновым Б. Ф. предложен метод моделирования случайных векторов с произвольным, но одинаковым для всех координат одномерным законом распределения и с заданной ковариационной матрицей. Такой подход базируется на реализации системы линейных разностных уравнений со случайными коэффициентами. Однако, как отмечает сам автор, реализация указанных разностных уравнений приводит к корреляции между последовательно генерируемыми векторами, что во многих случаях недопустимо.
В данной работе предлагается процедура моделирования многомерных величин, распределенных по законам, отличным от нормального, с заданными математическим ожиданием и ковариационной матрицей [72]. Она базируется на подходе, используемом для нормальных случайных векторов [49,51], и выборе <<удобного>> одномерного закона распределения для всех координат моделируемого вектора. В качестве одномерного закона используется семейство симметричных распределений (6.4).
К сожалению, реализованная процедура не позволяет моделировать многомерный закон с некоторой произвольной функцией распределения, на <<заданном>> расстоянии (определяемом в смысле некоторой меры) от многомерного нормального закона. Однако мы можем построить датчик, генерирующий псевдослучайные векторы по закону, отличающемуся от нормального (в соответствии с процессом моделирования), с известными математическим ожиданием и ковариационной матрицей. К тому же, на практике, при наблюдении выборок многомерных случайных векторов вставал бы вопрос об определении закона, которому они принадлежат. А покоординатный анализ сводится к одномерному случаю, который достаточно хорошо исследован и изучен.
Таким образом, на настоящем этапе исследований предложено направление решения задачи по моделированию закона с заданными математическим ожиданием и ковариационной матрицей с введением параметра в качестве меры различия между моделируемым и многомерным нормальным законами распределений.
1.5. Выводы
В данной главе диссертации рассмотрены некоторые критерии классического корреляционного анализа, связанные с проверкой гипотез о математическом ожидании, ковариационной матрице, парном, частном и множественном коэффициентах корреляции, из которых очевидна актуальность решения следующих задач:
· исследование эмпирических распределений статистик корреляционного анализа в случае многомерного нормального закона для выявления скорости их сходимости к соответствующим предельным распределениям;
· моделирование <<удобным>> способом многомерного закона, отличного от нормального;
· исследование распределений различных статистик классического корреляционного анализа в случае законов распределений, отличных от многомерного нормального.
Глава 2. Исследование критериев проверки гипотез о математических ожиданиях и дисперсиях при вероятностных законах, отличающихся от нормального
При поверке измерительных приборов, в задачах контроля качества и в
других приложениях часто возникает необходимость в проверке статистических
гипотез о значении математического ожидания ![]() или о значении дисперсии
или о значении дисперсии ![]() . В основе
применяемого классического аппарата проверки гипотез такого вида лежит
предположение о принадлежности наблюдаемых данных (ошибок измерений)
нормальному закону распределения. В то же время, не секрет, что ошибки
измерений приборов и систем во многих случаях не удается удовлетворительно
описать моделью нормального закона [97]. Необходимость проверки гипотез о
математических ожиданиях и дисперсиях при нарушении предположений о
нормальности наблюдаемого закона встречается во многих приложениях. Насколько
корректно в этом случае применение классического аппарата проверки данных
гипотез? Когда можно без боязни использовать классические критерии, а когда их
применение является некорректным, и как следует поступать в данном случае?
. В основе
применяемого классического аппарата проверки гипотез такого вида лежит
предположение о принадлежности наблюдаемых данных (ошибок измерений)
нормальному закону распределения. В то же время, не секрет, что ошибки
измерений приборов и систем во многих случаях не удается удовлетворительно
описать моделью нормального закона [97]. Необходимость проверки гипотез о
математических ожиданиях и дисперсиях при нарушении предположений о
нормальности наблюдаемого закона встречается во многих приложениях. Насколько
корректно в этом случае применение классического аппарата проверки данных
гипотез? Когда можно без боязни использовать классические критерии, а когда их
применение является некорректным, и как следует поступать в данном случае?
В работе [58] обобщены теоретические исследования Бартлетта, Гири и Гейена, в которых рассматривались вопросы об устойчивости критериев проверки гипотез о математических ожиданиях по отношению к виду наблюдаемого закона и содержатся указания на существенную зависимость от вида закона критериев проверки гипотез о дисперсиях. Сведения, которые практик может почерпнуть из этого, сводятся к тому, что при нарушении нормальности нельзя использовать классические результаты для проверки гипотез о дисперсиях, а для проверки гипотез о математических ожиданиях, по-видимому, можно, но с долей осторожности.
Целью данной главы явилось стремление установить при помощи численных исследований, что происходит с распределениями классических статистик, используемых в критериях проверки гипотез о математических ожиданиях и дисперсиях, если наблюдаемый закон в той или иной мере отличается от нормального; проверить, насколько будут корректны статистические выводы, базирующиеся на классических результатах, если нарушено предположение о нормальности; дать в руки исследователя необходимый математический аппарат, обеспечивающий корректность выводов при законах распределения, существенно отличающихся от нормального [76,80,107].
2.1. Классические критерии проверки гипотез о математических ожиданиях и дисперсиях
Пусть мы имеем выборку ![]() случайных величин, распределенных
по нормальному закону
случайных величин, распределенных
по нормальному закону ![]() . В этом случае задачи проверки
гипотез о математических ожиданиях и дисперсиях формулируются следующим
образом.
. В этом случае задачи проверки
гипотез о математических ожиданиях и дисперсиях формулируются следующим
образом.
В критерии проверки гипотез вида ![]() при известной дисперсии
при известной дисперсии ![]() используется
статистика
используется
статистика
![]() (2.1)
(2.1)
которая при справедливости гипотезы ![]() подчиняется нормальному распределению:
подчиняется нормальному распределению:
![]() [123].
Проверяемая гипотеза
[123].
Проверяемая гипотеза ![]() отклоняется при больших отклонениях
отклоняется при больших отклонениях
![]() от
от ![]() .
.
Для проверки гипотезы ![]() при неизвестной дисперсии
при неизвестной дисперсии ![]() используется
статистика
используется
статистика
![]() (2.2)
(2.2)
где ![]() ,
,
![]() . При
справедливости
. При
справедливости ![]() статистика
статистика
![]() распределена
как
распределена
как ![]() —
распределение Стьюдента [123].
—
распределение Стьюдента [123].
Для проверки гипотезы вида ![]() при известном математическом
ожидании
при известном математическом
ожидании ![]() вычисляется
статистика
вычисляется
статистика
![]() (2.3)
(2.3)
условным распределением которой является ![]() — распределение [123].
— распределение [123].
В критерии проверки гипотезы вида ![]() при неизвестном математическом
ожидании
при неизвестном математическом
ожидании ![]() используется
статистика
используется
статистика
![]() (2.4)
(2.4)
подчиняющаяся ![]() — распределению [123].
— распределению [123].
Для иллюстрации работоспособности применяемой методики исследований
приведем результаты моделирования эмпирических распределений данных статистик в
случае нормального закона регистрируемых наблюдений. В дальнейшем ![]() указывает на
объемы смоделированных выборок статистик рассматриваемых критериев.
указывает на
объемы смоделированных выборок статистик рассматриваемых критериев.
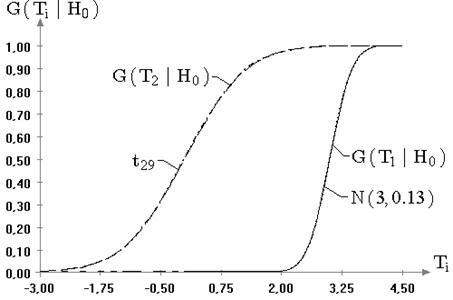
Рис. 2.1. Эмпирические и теоретические функции распределения
статистик ![]() ,
, ![]() при проверке гипотезы
при проверке гипотезы ![]() при известной (
при известной (![]() ) и неизвестной дисперсии:
) и неизвестной дисперсии: ![]() ;
; ![]()
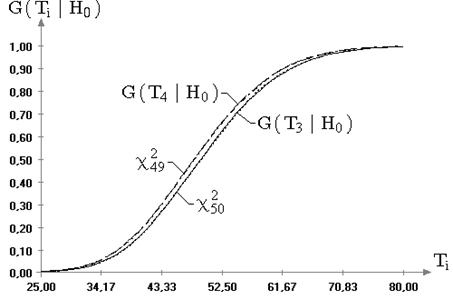
Рис. 2.2. Эмпирические и теоретические функции распределения
статистик ![]() и
и ![]() при проверке гипотезы
при проверке гипотезы ![]() при известном (
при известном (![]() ) и неизвестном
математическом ожидании:
) и неизвестном
математическом ожидании: ![]() ;
; ![]()
В качестве примера рассмотрены распределения статистик ![]() ,
, ![]() ,
, ![]() ,
, ![]() при проверяемых
гипотезах
при проверяемых
гипотезах ![]() и
и
![]() . На
рис. 2.1 отражены полученные в результате моделирования эмпирические распределения
статистик
. На
рис. 2.1 отражены полученные в результате моделирования эмпирические распределения
статистик ![]() ,
,
![]() и
теоретические распределения данных статистик при нормальности наблюдаемого
закона. Видно, что смоделированные распределения статистик, используемых при
проверке гипотез о значении математического ожидания, визуально совпадают со
своими предельными законами: нормальным и
и
теоретические распределения данных статистик при нормальности наблюдаемого
закона. Видно, что смоделированные распределения статистик, используемых при
проверке гипотез о значении математического ожидания, визуально совпадают со
своими предельными законами: нормальным и ![]() — распределением
Стьюдента. Количественной мерой близости полученных эмпирических распределений
статистик и теоретических предельных служат достигнутые уровни значимости
— распределением
Стьюдента. Количественной мерой близости полученных эмпирических распределений
статистик и теоретических предельных служат достигнутые уровни значимости ![]() по критериям
согласия
по критериям
согласия ![]() Пирсона,
Колмогорова,
Пирсона,
Колмогорова, ![]() Крамера– Мизеса"– Смирнова,
Крамера– Мизеса"– Смирнова,
![]() Андерсона"–
Дарлинга [111,112], где
Андерсона"–
Дарлинга [111,112], где ![]() — статистика соответствующего критерия
согласия,
— статистика соответствующего критерия
согласия, ![]() —
ее значение, вычисленное по конкретной выборке исследуемых статистик. Чем
больше достигнутый уровень значимости, чем ближе он к 1, тем лучше согласуется
эмпирическое распределение статистики с теоретическим. Приведенные в таблице на
рис. 2.1 значения достигнутых уровней значимости
—
ее значение, вычисленное по конкретной выборке исследуемых статистик. Чем
больше достигнутый уровень значимости, чем ближе он к 1, тем лучше согласуется
эмпирическое распределение статистики с теоретическим. Приведенные в таблице на
рис. 2.1 значения достигнутых уровней значимости ![]() для статистик
для статистик ![]() и
и ![]() говорят об очень
высокой близости полученных в результате моделирования эмпирических
распределений статистик к предельным. Аналогичная картина наблюдается на
рис. 2.2, где приведены результаты моделирования распределений статистик
говорят об очень
высокой близости полученных в результате моделирования эмпирических
распределений статистик к предельным. Аналогичная картина наблюдается на
рис. 2.2, где приведены результаты моделирования распределений статистик ![]() ,
, ![]() , используемых в
критериях проверки гипотез о значениях дисперсии.
, используемых в
критериях проверки гипотез о значениях дисперсии.
2.2. Распределения статистик 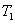 ,
, 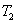 ,
, 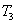 ,
,  при нарушении
предположений о нормальности
при нарушении
предположений о нормальности
В работе [68] распределения статистик ![]() ,
, ![]() были исследованы в случае принадлежности
наблюдаемых случайных величин распределениям экстремальных значений,
логистическому и Лапласа. В данном случае рассмотрено распределение, более
перспективное для описания ошибок измерений. Очень хорошей моделью для закона
распределения ошибок конкретной измерительной системы иногда оказывается распределение
из семейства с плотностью (6.4) и параметром формы
были исследованы в случае принадлежности
наблюдаемых случайных величин распределениям экстремальных значений,
логистическому и Лапласа. В данном случае рассмотрено распределение, более
перспективное для описания ошибок измерений. Очень хорошей моделью для закона
распределения ошибок конкретной измерительной системы иногда оказывается распределение
из семейства с плотностью (6.4) и параметром формы ![]() , так как данное семейство
охватывает широкий класс симметричных законов.
, так как данное семейство
охватывает широкий класс симметричных законов.
Далее будем рассматривать распределения статистик ![]() ,
, ![]() ,
, ![]() ,
, ![]() в случае принадлежности
наблюдаемых случайных величин указанному семейству распределений
в случае принадлежности
наблюдаемых случайных величин указанному семейству распределений ![]() ,
, ![]() . Предельные
распределения статистик
. Предельные
распределения статистик ![]() ,
, ![]() ,
, ![]() ,
, ![]() известны только для частного случая
этого семейства при
известны только для частного случая
этого семейства при ![]() (нормального закона).
(нормального закона).
Для статистик, вычисляемых по выборкам случайных величин ![]() ,
, ![]() , распределенных
по семейству (6.4) с параметром формы
, распределенных
по семейству (6.4) с параметром формы ![]() , введем обозначения
, введем обозначения ![]() .
.
Результаты моделирования выборок статистик ![]() и
и ![]() , где параметр
, где параметр ![]() изменялся в
диапазоне от 1 до 10, показали, что значимого изменения предельных распределений
статистик
изменялся в
диапазоне от 1 до 10, показали, что значимого изменения предельных распределений
статистик ![]() и
и
![]() , используемых
в критериях проверки гипотез о значениях математического ожидания (при
известной и неизвестной дисперсии), не происходит.
, используемых
в критериях проверки гипотез о значениях математического ожидания (при
известной и неизвестной дисперсии), не происходит.
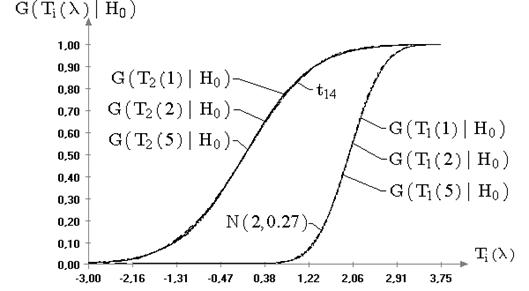
Рис. 2.3. Эмпирические и теоретические функции распределения
статистик ![]() и
и ![]() при проверке гипотезы
при проверке гипотезы ![]() при известной (
при известной (![]() ) и неизвестной дисперсии:
) и неизвестной дисперсии: ![]() ;
; ![]()
На рис. 2.3 в качестве примера представлены графики
теоретических предельных, соответствующих классическому случаю, и полученных
эмпирических функций распределения статистик ![]() и
и ![]() для объемов выборок
для объемов выборок ![]() , используемых
при проверке гипотезы
, используемых
при проверке гипотезы ![]() при известной (
при известной (![]() ) и неизвестной
дисперсиях. Визуальная близость распределений статистик, построенных в случае
принадлежности выборок семейству (6.4), к предельным (классическим)
распределениям, полученным для нормального закона, позволяет отметить, что
значимого изменения распределений статистик не произошло. Это же подтверждает
применение критериев согласия для проверки значимости отклонений
смоделированных эмпирических распределений статистик
) и неизвестной
дисперсиях. Визуальная близость распределений статистик, построенных в случае
принадлежности выборок семейству (6.4), к предельным (классическим)
распределениям, полученным для нормального закона, позволяет отметить, что
значимого изменения распределений статистик не произошло. Это же подтверждает
применение критериев согласия для проверки значимости отклонений
смоделированных эмпирических распределений статистик ![]() и
и ![]() от классических
предельных распределений (при нормальном законе наблюдаемых величин). Достигнутые
уровни значимости
от классических
предельных распределений (при нормальном законе наблюдаемых величин). Достигнутые
уровни значимости ![]() представлены в таблице 2.1.
представлены в таблице 2.1.
Таблица 2.1. Значения достигнутых уровней значимости критериев согласия для примера на рис. 2.3
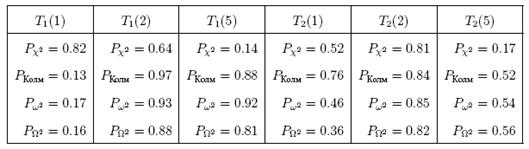
Результаты исследований распределений статистик ![]() и
и ![]() позволяют утверждать, что
в случае отклонений наблюдаемого закона от нормального (при сохранении симметричности),
использование классических предельных распределений для статистик
позволяют утверждать, что
в случае отклонений наблюдаемого закона от нормального (при сохранении симметричности),
использование классических предельных распределений для статистик ![]() и
и ![]() не нарушает
корректности выводов статистического анализа при проверке гипотез вида
не нарушает
корректности выводов статистического анализа при проверке гипотез вида ![]() .
.
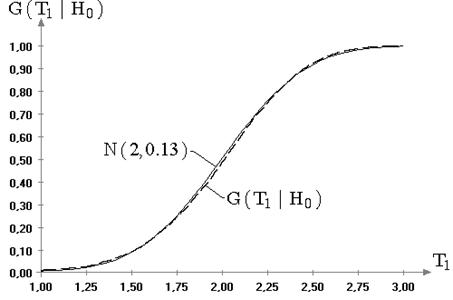
Рис. 2.4. Эмпирическая и теоретическая функции распределения
статистики ![]() ,
смоделированной по распределению минимального значения, при проверке гипотезы
,
смоделированной по распределению минимального значения, при проверке гипотезы ![]() для известной дисперсии (
для известной дисперсии (![]() ):
): ![]() ;
; ![]()
В случае несимметричных законов наблюдаемых величин, например, при
распределениях экстремальных значений, распределения статистик ![]() и
и ![]() претерпевают
значимые изменения, которые можно заметить как визуально, так и с
использованием критериев согласия. Соответствующий пример демонстрирует
картина, представленная на рис. 2.4. Пример свидетельствует все-таки об
ограниченной области устойчивости критериев проверки гипотез о математическом
ожидании. В таблице на рисунке приведены достигнутые значения уровня
значимости, которые свидетельствуют, что, не смотря на визуальную близость
эмпирического распределения статистики к теоретическому, в данном случае
гипотеза о нормальности статистики
претерпевают
значимые изменения, которые можно заметить как визуально, так и с
использованием критериев согласия. Соответствующий пример демонстрирует
картина, представленная на рис. 2.4. Пример свидетельствует все-таки об
ограниченной области устойчивости критериев проверки гипотез о математическом
ожидании. В таблице на рисунке приведены достигнутые значения уровня
значимости, которые свидетельствуют, что, не смотря на визуальную близость
эмпирического распределения статистики к теоретическому, в данном случае
гипотеза о нормальности статистики ![]() при уровне значимости
при уровне значимости ![]() должна быть отклонена.
должна быть отклонена.
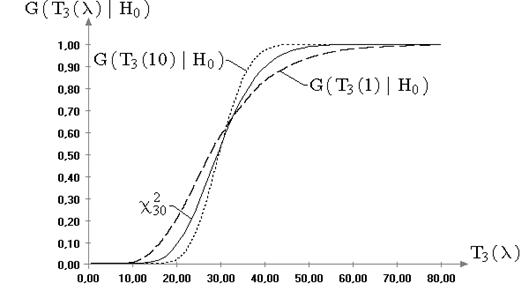
Рис. 2.5. Теоретическая и эмпирические функции распределения
статистики ![]() при
проверке гипотезы
при
проверке гипотезы ![]() при
известном (
при
известном (![]() )
математическом ожидании:
)
математическом ожидании: ![]() ;
; ![]()
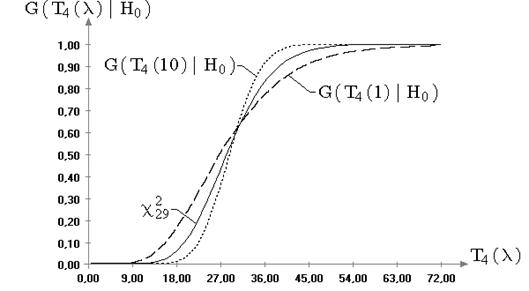
Рис. 2.6. Теоретическая и эмпирические функции распределения
статистики ![]() при
проверке гипотезы
при
проверке гипотезы ![]() при
неизвестном математическом ожидании:
при
неизвестном математическом ожидании: ![]() ;
;
![]()
В отличие от ![]() и
и ![]() распределения статистик
распределения статистик ![]() и
и ![]() , используемых в
критериях проверки гипотез о дисперсии, как в случае известного математического
ожидания, так и в случае неизвестного очень чувствительны к виду наблюдаемого
закона распределения. Иллюстрацией к сказанному являются рисунки 2.5 и 2.6,
на которых изображены графики эмпирических функций распределений статистик
, используемых в
критериях проверки гипотез о дисперсии, как в случае известного математического
ожидания, так и в случае неизвестного очень чувствительны к виду наблюдаемого
закона распределения. Иллюстрацией к сказанному являются рисунки 2.5 и 2.6,
на которых изображены графики эмпирических функций распределений статистик ![]() и
и ![]() , смоделированных
при семействе распределений (6.4) с параметром формы
, смоделированных
при семействе распределений (6.4) с параметром формы ![]() равным 1 и 10. На
рисунках приведены также предельные распределения статистик
равным 1 и 10. На
рисунках приведены также предельные распределения статистик ![]() и
и ![]() в случае нормального
закона (
в случае нормального
закона (![]() и
и ![]() —
распределения, соответственно).
—
распределения, соответственно).
Из представленной на рис. 2.5 картины очевидно, что
распределения статистики ![]() , смоделированные при выборках
случайных величин, принадлежащих семейству распределений (6.4) с
параметром формы не равным 2, существенно отличаются от предельного
распределения, полученного для нормального закона. Аналогичную зависимость от
вида наблюдаемого закона демонстрирует статистика
, смоделированные при выборках
случайных величин, принадлежащих семейству распределений (6.4) с
параметром формы не равным 2, существенно отличаются от предельного
распределения, полученного для нормального закона. Аналогичную зависимость от
вида наблюдаемого закона демонстрирует статистика ![]() при проверке гипотезы о значении
дисперсии при неизвестном математическом ожидании (см. рис. 2.6).
при проверке гипотезы о значении
дисперсии при неизвестном математическом ожидании (см. рис. 2.6).
Результаты проведенных исследований говорят о том, что распределения статистик, используемых при проверке гипотез о дисперсии (математическое ожидание известно или неизвестно), значимо отличаются от классических предельных при отклонениях наблюдаемого закона от нормального. Поэтому при использовании классических процедур для проверки гипотез о дисперсии целесообразно удостовериться в том, что наблюдаемый закон является нормальным, применяя соответствующие критерии проверки нормальности.
Таким образом, приводимые результаты показывают, с одной стороны,
высокую устойчивость к отклонениям от нормальности наблюдаемых величин
критериев проверки гипотез о математических ожиданиях. А, с другой стороны, —
неустойчивость критериев, используемых при проверке гипотез о дисперсиях. В то
же время результаты подтверждают возможность построения моделей предельных
распределений для статистик ![]() и
и ![]() при произвольных наблюдаемых
законах случайных величин, что актуально для различных приложений задач
статистического анализа данных.
при произвольных наблюдаемых
законах случайных величин, что актуально для различных приложений задач
статистического анализа данных.
Для построения приближенных моделей, наилучшим образом описывающих
распределения статистик ![]() и
и ![]() при конкретных значениях
при конкретных значениях ![]() и
и ![]() , принципиальных
трудностей нет. К сожалению, не удается построить аналитические модели
распределений данных статистик с параметрами, зависящими от
, принципиальных
трудностей нет. К сожалению, не удается построить аналитические модели
распределений данных статистик с параметрами, зависящими от ![]() и
и ![]() . Поэтому на основании
результатов статистического моделирования были вычислены таблицы верхних
процентных точек (квантилей) для ряда значений
. Поэтому на основании
результатов статистического моделирования были вычислены таблицы верхних
процентных точек (квантилей) для ряда значений ![]() и
и ![]() . Процентные точки рассчитывались по
выборкам значений статистик достаточно больших объемов (
. Процентные точки рассчитывались по
выборкам значений статистик достаточно больших объемов (![]() ,
, ![]() и
и ![]() ), а затем усреднялись по
ряду экспериментов.
), а затем усреднялись по
ряду экспериментов.
Полученные процентные точки для статистик ![]() и
и ![]() при параметре формы
при параметре формы ![]() семейства распределений (6.4),
равном 1, 1.5, 3, 4, 5 и 10 приведены в таблицах 2.2 и 2.3 соответственно.
Значения процентных точек при параметре формы
семейства распределений (6.4),
равном 1, 1.5, 3, 4, 5 и 10 приведены в таблицах 2.2 и 2.3 соответственно.
Значения процентных точек при параметре формы ![]() , приведенные в таблицах,
соответствуют предельным распределениям статистик при нормальном законе наблюдаемых
величин.
, приведенные в таблицах,
соответствуют предельным распределениям статистик при нормальном законе наблюдаемых
величин.
Таблица 2.2. Верхние процентные точки для статистики ![]() в случае принадлежности
наблюдаемого закона семейству распределений (6.4) с параметром формы
в случае принадлежности
наблюдаемого закона семейству распределений (6.4) с параметром формы ![]()
|
|
|
l = 1 |
l = 1,5 |
l = 2 |
l = 3 |
l = 4 |
l = 5 |
l = 10 |
|
n = 15 |
a = 0,15 |
22,94 |
21,45 |
20,64 |
19,76 |
19,39 |
19,18 |
18,81 |
|
a = 0,1 |
25,98 |
23,54 |
22,34 |
21,06 |
20,58 |
20,28 |
19,77 |
|
|
a = 0,05 |
31,38 |
26,98 |
25,01 |
23,08 |
22,41 |
21,96 |
21,22 |
|
|
a = 0,025 |
37,02 |
30,23 |
27,46 |
24,88 |
24,04 |
23,45 |
22,51 |
|
|
a = 0,01 |
44,36 |
34,40 |
30,59 |
27,03 |
26,00 |
25,21 |
24,02 |
|
|
n = 30 |
a = 0,15 |
41,85 |
39,31 |
38,01 |
36,79 |
36,21 |
35,89 |
35,37 |
|
a = 0,1 |
45,97 |
42,09 |
40,26 |
38,60 |
37,84 |
37,41 |
36,71 |
|
|
a = 0,05 |
52,92 |
46,49 |
43,80 |
41,37 |
40,28 |
39,70 |
38,70 |
|
|
a = 0,025 |
59,56 |
50,59 |
46,97 |
43,80 |
42,47 |
41,72 |
40,46 |
|
|
a = 0,01 |
68,51 |
55,65 |
50,88 |
46,78 |
45,08 |
44,15 |
42,52 |
|
|
n = 50 |
a = 0,15 |
65,86 |
62,02 |
60,30 |
58,77 |
58,02 |
57,60 |
56,91 |
|
a = 0,1 |
70,83 |
65,50 |
63,15 |
61,00 |
60,04 |
59,51 |
58,61 |
|
|
a = 0,05 |
78,47 |
70,91 |
67,51 |
64,42 |
63,10 |
62,36 |
61,17 |
|
|
a = 0,025 |
85,83 |
75,66 |
71,34 |
67,51 |
65,86 |
64,94 |
63,39 |
|
|
a = 0,01 |
95,36 |
81,92 |
76,15 |
71,24 |
69,22 |
67,98 |
66,05 |
|
|
n = 100 |
a = 0,15 |
122,67 |
116,99 |
114,57 |
112,34 |
111,27 |
110,69 |
109,77 |
|
a = 0,1 |
129,31 |
121,54 |
118,47 |
115,47 |
114,13 |
113,38 |
112,15 |
|
|
a = 0,05 |
139,98 |
128,64 |
124,29 |
120,07 |
118,37 |
117,38 |
115,67 |
|
|
a = 0,025 |
149,80 |
135,17 |
129,33 |
124,27 |
122,14 |
120,90 |
118,78 |
|
|
a = 0,01 |
162,04 |
143,38 |
135,95 |
129,27 |
126,64 |
125,05 |
122,42 |
Таблица 2.3. Верхние процентные точки для статистики ![]() в случае принадлежности
наблюдаемого закона семейству распределений (6.4) с параметром формы
в случае принадлежности
наблюдаемого закона семейству распределений (6.4) с параметром формы ![]()
|
|
|
l = 1 |
l = 1,5 |
l = 2 |
l = 3 |
l = 4 |
l = 5 |
l = 10 |
|
n = 15 |
a = 0,15 |
21,49 |
20,16 |
19,40 |
18,65 |
18,34 |
18,14 |
17,82 |
|
a = 0,1 |
24,38 |
22,19 |
21,03 |
19,95 |
19,53 |
19,26 |
18,80 |
|
|
a = 0,05 |
29,52 |
25,46 |
23,65 |
21,92 |
21,34 |
20,94 |
20,27 |
|
|
a = 0,025 |
34,79 |
28,64 |
26,12 |
23,71 |
22,95 |
22,41 |
21,56 |
|
|
a = 0,01 |
41,88 |
32,70 |
29,25 |
25,85 |
24,94 |
24,22 |
23,09 |
|
|
n = 30 |
a = 0,15 |
40,54 |
38,09 |
36,88 |
35,71 |
35,17 |
34,89 |
34,39 |
|
a = 0,1 |
44,53 |
40,83 |
39,11 |
37,49 |
36,79 |
36,42 |
35,73 |
|
|
a = 0,05 |
51,36 |
45,20 |
42,60 |
40,25 |
39,25 |
38,71 |
37,73 |
|
|
a = 0,025 |
57,85 |
49,20 |
45,74 |
42,70 |
41,41 |
40,77 |
39,51 |
|
|
a = 0,01 |
66,49 |
54,21 |
49,59 |
45,61 |
44,01 |
43,13 |
41,60 |
|
|
n = 50 |
a = 0,15 |
64,62 |
60,90 |
59,24 |
57,70 |
56,99 |
56,59 |
55,92 |
|
a = 0,1 |
69,58 |
64,30 |
62,06 |
59,95 |
59,01 |
58,51 |
57,63 |
|
|
a = 0,05 |
77,18 |
69,65 |
66,39 |
63,35 |
62,07 |
61,37 |
60,17 |
|
|
a = 0,025 |
84,42 |
74,42 |
70,20 |
66,46 |
64,79 |
63,96 |
62,41 |
|
|
a = 0,01 |
93,75 |
80,63 |
74,94 |
70,21 |
68,13 |
66,98 |
65,05 |
|
|
n = 100 |
a = 0,15 |
121,51 |
115,87 |
113,54 |
111,29 |
110,26 |
109,71 |
108,77 |
|
a = 0,1 |
128,08 |
120,45 |
117,35 |
114,43 |
113,11 |
112,39 |
111,15 |
|
|
a = 0,05 |
138,70 |
127,50 |
123,22 |
119,07 |
117,36 |
116,38 |
114,67 |
|
|
a = 0,025 |
148,27 |
134,04 |
128,29 |
123,18 |
121,07 |
119,87 |
117,79 |
|
|
a = 0,01 |
160,22 |
142,27 |
134,71 |
128,13 |
125,55 |
124,04 |
121,34 |
2.3. Выводы
Таким образом, численные исследования подтвердили теоретические
результаты, приведенные в [58], а именно: устойчивость распределений статистик ![]() и
и ![]() , используемых в
критериях проверки гипотез о математических ожиданиях, к отклонениям наблюдаемого
закона от нормального и неустойчивость распределений статистик
, используемых в
критериях проверки гипотез о математических ожиданиях, к отклонениям наблюдаемого
закона от нормального и неустойчивость распределений статистик ![]() ,
, ![]() . Эмпирические
распределения статистик
. Эмпирические
распределения статистик ![]() и
и ![]() хорошо согласуются с предельными, полученными
в предположении о нормальности наблюдаемого закона. Это позволяет на практике
корректно применять классические результаты при наблюдаемых законах, существенно
отличающихся от нормального. В частности, в таких ситуациях можно уверенно
руководствоваться стандартом [39].
хорошо согласуются с предельными, полученными
в предположении о нормальности наблюдаемого закона. Это позволяет на практике
корректно применять классические результаты при наблюдаемых законах, существенно
отличающихся от нормального. В частности, в таких ситуациях можно уверенно
руководствоваться стандартом [39].
Полученные в данном разделе результаты подчеркивают общую закономерность: критерии, связанные с проверкой гипотез о математических ожиданиях устойчивы к отклонениям наблюдаемых величин от нормального закона. Это было показано при исследовании распределений статистик, используемых при проверке гипотез о векторе математических ожиданий многомерного закона распределения [74].
В то же время, как предполагалось [58], распределения статистик ![]() и
и ![]() очень существенно
зависят от вида наблюдаемого закона. Если наблюдаемый закон значимо отличается
от нормального, использование классических результатов для данных критериев недопустимо,
так как такая попытка неизбежно приведет к некорректным выводам. В тех
ситуациях, когда хорошей моделью для наблюдаемых случайных величин оказывается
семейство симметричных распределений (6.4) с параметром формы
очень существенно
зависят от вида наблюдаемого закона. Если наблюдаемый закон значимо отличается
от нормального, использование классических результатов для данных критериев недопустимо,
так как такая попытка неизбежно приведет к некорректным выводам. В тех
ситуациях, когда хорошей моделью для наблюдаемых случайных величин оказывается
семейство симметричных распределений (6.4) с параметром формы ![]() , можно воспользоваться
таблицами процентных точек, полученными в данной главе.
, можно воспользоваться
таблицами процентных точек, полученными в данной главе.
Глава 3. Исследование критериев проверки гипотез о векторе математических ожиданий и ковариационной матрице
В данном разделе методами компьютерного моделирования исследуются распределения статистик критериев проверки гипотез о векторе математических ожиданий и ковариационной матрице при наблюдении случайных величин, подчиняющихся различным многомерным законам распределения [70, 71, 73–75, 78, 79, 83].
3.1. Классические критерии проверки гипотез о векторе математических ожиданий и ковариационной матрице
3.1.1. Проверка гипотез о векторе математических ожиданий
Одной из важных статистических проблем является проблема проверки
гипотезы о том, что вектор среднего значения нормального распределения является
данным вектором ![]() . Такая задача очень часто возникает
на практике, когда, например, на основании наблюдений некоторого
технологического процесса желают убедиться, что эти показатели равны
номинальному значению
. Такая задача очень часто возникает
на практике, когда, например, на основании наблюдений некоторого
технологического процесса желают убедиться, что эти показатели равны
номинальному значению ![]() , т.е. процесс протекает нормально,
а отклонения наблюдаемых значений от номинальных объясняются лишь ошибками
наблюдений (измерений). При решении этой задачи возможны две ситуации: ковариационная
матрица
, т.е. процесс протекает нормально,
а отклонения наблюдаемых значений от номинальных объясняются лишь ошибками
наблюдений (измерений). При решении этой задачи возможны две ситуации: ковариационная
матрица ![]() может
быть известна из ранее проводимых экспериментов, или неизвестна, тогда в
процессе вычислений для нее будет построена оценка.
может
быть известна из ранее проводимых экспериментов, или неизвестна, тогда в
процессе вычислений для нее будет построена оценка.
Для проверки гипотезы ![]() в зависимости от априорной
информации могут использоваться различные критерии.
в зависимости от априорной
информации могут использоваться различные критерии.
Ковариационная матрица ![]() известна. В этом случае вычисляется
статистика
известна. В этом случае вычисляется
статистика
![]() (3.1)
(3.1)
которая при справедливой гипотезе ![]() в качестве предельного распределения
в качестве предельного распределения
![]() имеет
имеет ![]() –распределение, с
числом степеней свободы
–распределение, с
числом степеней свободы ![]() [33].
[33].
Ковариационная матрица ![]() неизвестна. Тогда в критерии
проверки гипотезы используется статистика
неизвестна. Тогда в критерии
проверки гипотезы используется статистика
![]() (3.2)
(3.2)
которая при справедливости гипотезы ![]() в пределе подчиняется распределению
Фишера с параметрами
в пределе подчиняется распределению
Фишера с параметрами ![]() и
и ![]() :
: ![]() [33].
[33].
3.1.2. Проверка гипотез о ковариационной матрице
Не менее важной задачей классического корреляционного анализа
(вектор ![]() принадлежит
нормальному закону) является проверка гипотезы о ковариационной матрице
принадлежит
нормальному закону) является проверка гипотезы о ковариационной матрице ![]() , где
, где ![]() "—
номинальное значение ковариационной матрицы. В этом случае подразумевается, что
вектор математических ожиданий будет оцениваться по данной выборке. Если
одновременно проверяется гипотеза и о векторе математических ожиданий, тогда
проверяемая гипотеза имеет вид
"—
номинальное значение ковариационной матрицы. В этом случае подразумевается, что
вектор математических ожиданий будет оцениваться по данной выборке. Если
одновременно проверяется гипотеза и о векторе математических ожиданий, тогда
проверяемая гипотеза имеет вид ![]() .
.
В критериях проверки данных гипотез используются следующие статистики.
Если проверяется гипотеза ![]() (математическое ожидание
(математическое ожидание ![]() неизвестно),
тогда вычисляется статистика
неизвестно),
тогда вычисляется статистика
![]() (3.3)
(3.3)
где
![]()
При справедливости гипотезы ![]() данная статистика имеет
данная статистика имеет ![]() –распределение с
числом степеней свободы
–распределение с
числом степеней свободы ![]() :
: ![]() [33].
[33].
Если проверяется гипотеза ![]() , то используется статистика,
, то используется статистика,
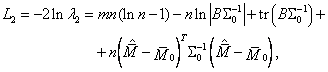 (3.4)
(3.4)
которая при справедливой гипотезе ![]() в качестве предельного
распределения
в качестве предельного
распределения ![]() имеет
имеет
![]() –
распределение, с числом степеней свободы
–
распределение, с числом степеней свободы ![]() [33].
[33].
Подчеркнем, что рассмотренные выше статистики имеют в качестве предельных указанные распределения лишь при наблюдении многомерного нормального закона. Как изменятся предельные распределения статистик, если наблюдаемый многомерный закон отличается от нормального, заранее сказать нельзя.
3.2. Исследование распределений статистик критериев в случае принадлежности наблюдений нормальному закону
На первом этапе методами статистического моделирования исследовались распределения статистик корреляционного анализа при условии, что наблюдения принадлежат многомерному нормальному закону. Близость получаемых эмпирических распределений статистик, в данном случае, известным предельным законам, является основанием, подтверждающим корректность применения используемой методики при анализе достоверности результатов последующих исследований.
Моделирование и исследование эмпирических распределений статистик классического корреляционного анализа показало, что они хорошо согласуются с соответствующими теоретическими предельными распределениями.
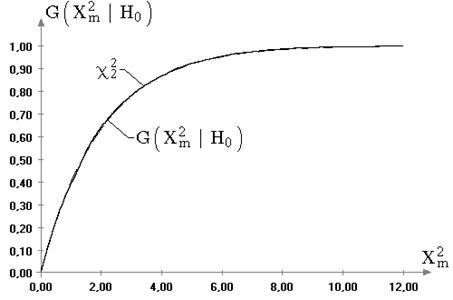
Рис. 3.1. Эмпирическая и теоретическая функции распределения
статистики ![]() при
проверке гипотезы
при
проверке гипотезы ![]() (ковариационная
матрица известна):
(ковариационная
матрица известна): ![]() ,
, ![]()
Например, на рис. 3.1 представлены полученное в результате
моделирования эмпирическое распределение статистики ![]() (3.1) и соответствующее
предельное
(3.1) и соответствующее
предельное ![]() —
распределение при проверке гипотезы
—
распределение при проверке гипотезы ![]() (ковариационная матрица
(ковариационная матрица ![]() известна) для
размерности
известна) для
размерности ![]() и
объеме выборки
и
объеме выборки ![]() ,
где использовались
,
где использовались
![]()
Рисунок дополнен таблицей, где отражены результаты проверки согласия
эмпирического распределения с теоретическим предельным по критериям ![]() Пирсона,
Колмогорова,
Пирсона,
Колмогорова, ![]() и
и
![]() Мизеса
[43,85]: по каждому из критериев приведен достигнутый уровень значимости
Мизеса
[43,85]: по каждому из критериев приведен достигнутый уровень значимости ![]() , где
, где ![]() — предельное
распределение статистики
— предельное
распределение статистики ![]() соответствующего критерия согласия
при справедливости проверяемой гипотезы
соответствующего критерия согласия
при справедливости проверяемой гипотезы ![]() .
.
В ходе исследований объемы выборок значений статистик ![]() , формируемых в результате
моделирования, если не оговариваются явно, в данном разделе и далее предполагаются
равными 5000.
, формируемых в результате
моделирования, если не оговариваются явно, в данном разделе и далее предполагаются
равными 5000.
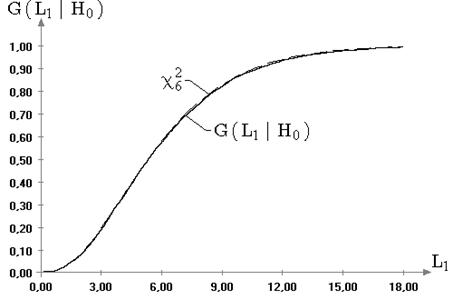
Рис. 3.2. Эмпирическая и теоретическая функции
распределения статистики ![]() при
проверке гипотезы
при
проверке гипотезы ![]() (математическое
ожидание неизвестно):
(математическое
ожидание неизвестно): ![]() ,
, ![]()
На рис. 3.2 приведен пример, где отображены полученная в
результате моделирования эмпирическая и теоретическая функции распределения
статистики ![]() ,
используемой для проверки гипотезы
,
используемой для проверки гипотезы ![]() (математическое ожидание
неизвестно), где использовались следующие значения параметров
(математическое ожидание
неизвестно), где использовались следующие значения параметров ![]() и
и ![]() ,
,

Приведенные примеры подтверждают, что эмпирические распределения
статистик, используемых в критериях проверки гипотез о векторе математических
ожиданий и ковариационной матрице при наблюдении многомерного нормального
закона распределения, действительно хорошо описываются соответствующими
предельными законами, полученными в [33]. Аналогичная картина, подтверждающая
очень хорошее согласие смоделированных эмпирических распределений статистик с
классическими предельными, наблюдается и для распределений статистик ![]() (3.2) и
(3.2) и ![]() (3.4).
(3.4).
Исследование сходимости распределений рассматриваемых статистик к
предельным в зависимости от объема выборки ![]() многомерного нормального закона
показало, что для статистик [
многомерного нормального закона
показало, что для статистик [![]() (3.1),
(3.1), ![]() (3.3) и
(3.3) и ![]() (3.4)],
параметры предельных распределений которых не зависят от объема выборки,
эмпирические распределения статистик оказываются близки к предельным уже при
выборках сравнительно небольшого объема
(3.4)],
параметры предельных распределений которых не зависят от объема выборки,
эмпирические распределения статистик оказываются близки к предельным уже при
выборках сравнительно небольшого объема ![]() . Так, у статистики
. Так, у статистики ![]() высокий
достигаемый уровень значимости по критериям согласия наблюдается, начиная с
объемов выборки
высокий
достигаемый уровень значимости по критериям согласия наблюдается, начиная с
объемов выборки ![]() , а для статистик
, а для статистик ![]() и
и ![]() — с
— с ![]() .
.
Предельное распределение статистики ![]() зависит от объема выборки случайной
величины
зависит от объема выборки случайной
величины ![]() .
Поэтому предельное распределение как бы <<подстраивается>> под
объем выборки случайного вектора. Вследствие этого уже при малых объемах
выборок
.
Поэтому предельное распределение как бы <<подстраивается>> под
объем выборки случайного вектора. Вследствие этого уже при малых объемах
выборок ![]() наблюдаются
достаточно высокие достигаемые уровни значимости при проверке соответствия
эмпирических распределений статистик предельным законам по критериям согласия.
наблюдаются
достаточно высокие достигаемые уровни значимости при проверке соответствия
эмпирических распределений статистик предельным законам по критериям согласия.
Отметим, что при исследовании не было выявлено существенного влияния
размерности случайного вектора ![]() на сходимость распределений
соответствующих статистик к предельным. Исследования проводились для
размерности случайного вектора в диапазоне
на сходимость распределений
соответствующих статистик к предельным. Исследования проводились для
размерности случайного вектора в диапазоне ![]() .
.
3.3. Исследование распределений статистик при законах, отличающихся от нормального
Далее проводились исследования распределений статистик для законов
многомерных величин, моделируемых в соответствии с предложенной и описанной в
главе 6 процедурой. Процедура моделирования опирается на семейство
распределений (6.4) и позволяет генерировать псевдослучайные векторы, подчиняющиеся
многомерным симметричным законам, более островершинным (![]() ) или более плосковершинным
(
) или более плосковершинным
(![]() ) по
сравнению с нормальным законом. Исследования были проведены при значениях параметра
) по
сравнению с нормальным законом. Исследования были проведены при значениях параметра
![]() . Это
ограничение обусловлено тем, что предельным случаем семейства распределений (6.4)
при
. Это
ограничение обусловлено тем, что предельным случаем семейства распределений (6.4)
при ![]() является
распределение Коши, которое представляет собой пример
<<патологического>> распределения: не существует математического
ожидания и дисперсия расходится. Поэтому в результате моделирования
псевдослучайных векторов при параметре
является
распределение Коши, которое представляет собой пример
<<патологического>> распределения: не существует математического
ожидания и дисперсия расходится. Поэтому в результате моделирования
псевдослучайных векторов при параметре ![]() мы получаем закон с ковариационной
матрицей близкой к вырожденной.
мы получаем закон с ковариационной
матрицей близкой к вырожденной.
Распределения статистик корреляционного анализа при многомерных
законах, отличающихся от нормального и моделируемых в соответствии с
предлагаемой процедурой, базирующейся на семействе распределений (6.4) с
параметром формы ![]() , определяющим вид закона, исследовались
при различных объемах выборок
, определяющим вид закона, исследовались
при различных объемах выборок ![]() и различной размерности
и различной размерности ![]() случайных
величин. Ниже приведены примеры моделирования распределений исследуемых
статистик с отражением соответствующих предельных распределений классических
статистик. На рисунках представлены значения достигнутых уровней значимости по
критериям
случайных
величин. Ниже приведены примеры моделирования распределений исследуемых
статистик с отражением соответствующих предельных распределений классических
статистик. На рисунках представлены значения достигнутых уровней значимости по
критериям ![]() Пирсона,
Колмогорова,
Пирсона,
Колмогорова, ![]() и
и
![]() Мизеса
при проверке согласия полученных в результате моделирования эмпирических
распределений статистик с предельными распределениями классических статистик.
Мизеса
при проверке согласия полученных в результате моделирования эмпирических
распределений статистик с предельными распределениями классических статистик.
Для статистик, вычисляемых по выборкам псевдослучайных векторов,
смоделированных с использованием параметра формы ![]() , введем новые обозначения, где в
скобках отразим зависимость распределения статистики от параметра
, введем новые обозначения, где в
скобках отразим зависимость распределения статистики от параметра ![]() . Например, для
статистики
. Например, для
статистики ![]() будем
использовать новое обозначение
будем
использовать новое обозначение ![]() .
.
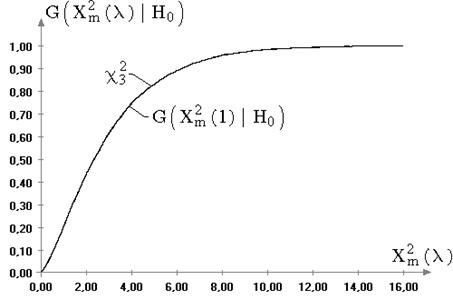
Рис. 3.3. Распределение статистики ![]() и классическое предельное
и классическое предельное ![]() – распределение (
– распределение (![]() ,
, ![]() )
)
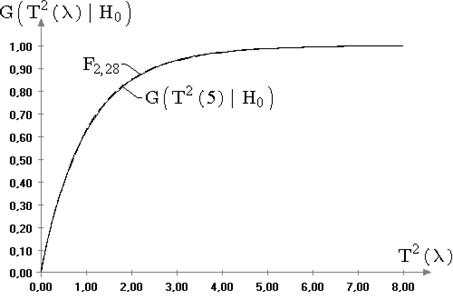
Рис. 3.4. Распределение статистики ![]() и классическое предельное
и классическое предельное ![]() – распределение (
– распределение (![]() ,
, ![]() )
)
На рис. 3.3 показан вид распределения статистики ![]() в случае закона,
смоделированного при параметре
в случае закона,
смоделированного при параметре ![]() . Высокие достигнутые уровни значимости
по всем критериям согласия и визуальная близость полученного эмпирического
распределения статистики
. Высокие достигнутые уровни значимости
по всем критериям согласия и визуальная близость полученного эмпирического
распределения статистики ![]() и предельного в случае многомерного
нормального закона
и предельного в случае многомерного
нормального закона ![]() — распределения, позволяют
утверждать, что вид предельного распределения статистики значимо не изменился.
Аналогичная картина видна на рис. 3.4, где показаны эмпирическое распределение
статистики
— распределения, позволяют
утверждать, что вид предельного распределения статистики значимо не изменился.
Аналогичная картина видна на рис. 3.4, где показаны эмпирическое распределение
статистики ![]() и
предельное в классическом случае распределение Фишера.
и
предельное в классическом случае распределение Фишера.
Отметим, что при моделировании (6.6)– (6.7) многомерных величин
по несимметричным одномерным законам (в качестве примеров рассматривалась
принадлежность ![]() ,
распределениям экстремальных значений) распределения статистик, используемых в
критериях проверки гипотез о векторе математических ожиданий, по–прежнему
хорошо описываются предельными распределениями, полученными в предположении о
нормальности наблюдаемой выборки.
,
распределениям экстремальных значений) распределения статистик, используемых в
критериях проверки гипотез о векторе математических ожиданий, по–прежнему
хорошо описываются предельными распределениями, полученными в предположении о
нормальности наблюдаемой выборки.
Проведенные исследования распределений статистик ![]() и
и ![]() показали, что в случае
многомерных законов, достаточно существенно отличающихся от нормального (более
островершинных или более плосковершинных, и даже в случае многомерного закона,
построенного по несимметричному одномерному распределению), значимого изменения
предельных распределений статистик не происходит. Это позволяет утверждать, что
статистические выводы, опирающиеся на классический аппарат в исследованных
задачах корреляционного анализа о векторе математических ожиданий, будут
оставаться корректными и при нарушении предположений о нормальности
наблюдаемого многомерного закона при условии существования вектора
математических ожиданий и невырожденности ковариационной матрицы.
показали, что в случае
многомерных законов, достаточно существенно отличающихся от нормального (более
островершинных или более плосковершинных, и даже в случае многомерного закона,
построенного по несимметричному одномерному распределению), значимого изменения
предельных распределений статистик не происходит. Это позволяет утверждать, что
статистические выводы, опирающиеся на классический аппарат в исследованных
задачах корреляционного анализа о векторе математических ожиданий, будут
оставаться корректными и при нарушении предположений о нормальности
наблюдаемого многомерного закона при условии существования вектора
математических ожиданий и невырожденности ковариационной матрицы.
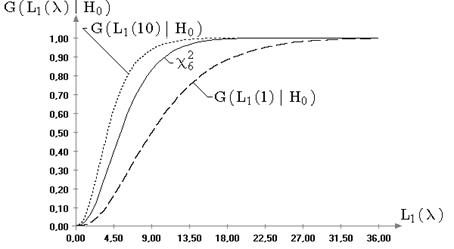
Рис. 3.5. Распределения статистик ![]() ,
, ![]() и предельное распределение
статистики
и предельное распределение
статистики ![]() :
: ![]() – распределение (
– распределение (![]() ,
, ![]() )
)
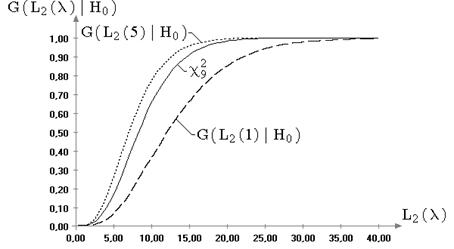
Рис. 3.6. Распределения статистик ![]() ,
, ![]() и предельное распределение
статистики
и предельное распределение
статистики ![]() :
: ![]() – распределение (
– распределение (![]() ,
, ![]() )
)
В отличие от ![]() и
и ![]() распределения статистик
распределения статистик ![]() и
и ![]() , используемых в
критериях проверки гипотез о ковариационной матрице, как в случае известного
вектора математических ожиданий, так и в случае неизвестного, очень
чувствительны к виду наблюдаемого закона распределения. Это хорошо видно на
приведенных в качестве примера рисунках 3.5 и 3.6, на которых отображены
графики эмпирических распределений статистик
, используемых в
критериях проверки гипотез о ковариационной матрице, как в случае известного
вектора математических ожиданий, так и в случае неизвестного, очень
чувствительны к виду наблюдаемого закона распределения. Это хорошо видно на
приведенных в качестве примера рисунках 3.5 и 3.6, на которых отображены
графики эмпирических распределений статистик ![]() ,
, ![]() и предельные распределения
статистик
и предельные распределения
статистик ![]() ,
,
![]() в
случае нормального закона (
в
случае нормального закона (![]() и
и ![]() — распределения, соответственно).
— распределения, соответственно).
Так, из представленной на рис. 3.5 картины очевидно, что
эмпирические распределения статистики ![]() , смоделированные при значении
параметра формы 1 и 10 семейства распределений (6.4), существенно
отличаются от предельного распределения статистики
, смоделированные при значении
параметра формы 1 и 10 семейства распределений (6.4), существенно
отличаются от предельного распределения статистики ![]() , полученного в случае
принадлежности наблюдений многомерному нормальному закону. Аналогичную
зависимость от вида наблюдаемого закона демонстрирует статистика
, полученного в случае
принадлежности наблюдений многомерному нормальному закону. Аналогичную
зависимость от вида наблюдаемого закона демонстрирует статистика ![]() при проверке
гипотезы о ковариационной матрице и математическом ожидании
при проверке
гипотезы о ковариационной матрице и математическом ожидании ![]() (см.
рис. 3.6).
(см.
рис. 3.6).
Результаты проведенных исследований говорят о том, что распределения статистик, используемых при проверке гипотез о ковариационной матрице, значимо отличаются от классических предельных при отклонениях наблюдаемого закона от многомерного нормального. Поэтому при использовании классических процедур для проверки гипотез о ковариационной матрице, также как в одномерном случае при проверке гипотез о дисперсии, целесообразно удостовериться в том, что наблюдаемый закон является нормальным, применяя соответствующие критерии проверки нормальности.
Для проверки предположения об устойчивости статистик ![]() и
и ![]() к отклонению
наблюдаемого закона от нормального, было проведено исследование распределений
данных статистик в случае многомерного распределения Стьюдента (6.19).
Напомним, что с ростом числа степеней свободы (
к отклонению
наблюдаемого закона от нормального, было проведено исследование распределений
данных статистик в случае многомерного распределения Стьюдента (6.19).
Напомним, что с ростом числа степеней свободы (![]() ) распределение Стьюдента стремится
к нормальному закону.
) распределение Стьюдента стремится
к нормальному закону.
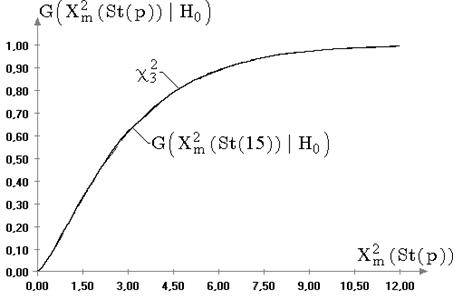
Рис. 3.7. Распределение статистики ![]() , построенной по многомерному
закону Стьюдента с числом степеней свободы
, построенной по многомерному
закону Стьюдента с числом степеней свободы ![]() , и классическое предельное
, и классическое предельное ![]() – распределение (
– распределение (![]() ,
, ![]() )
)
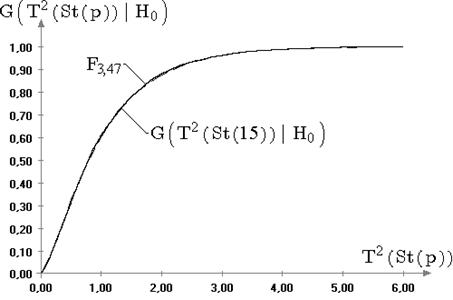
Рис. 3.8. Распределение статистики ![]() , построенной по многомерному
закону Стьюдента с
, построенной по многомерному
закону Стьюдента с ![]() степенями
свободы, и классическое предельное
степенями
свободы, и классическое предельное ![]() – распределение
(
– распределение
(![]() ,
, ![]() )
)
На приведенном рис. 3.7 видно, что, действительно, эмпирическое
распределение статистики ![]() в случае принадлежности наблюдаемой
многомерной случайной величины распределению Стьюдента хорошо описывается
в случае принадлежности наблюдаемой
многомерной случайной величины распределению Стьюдента хорошо описывается ![]() –
распределением. Здесь статистика
–
распределением. Здесь статистика ![]() была построена по распределению
Стьюдента с числом степеней свободы
была построена по распределению
Стьюдента с числом степеней свободы ![]() и следующих параметрах
моделирования:
и следующих параметрах
моделирования: ![]() ,
,
![]() .
.
Отметим, что в случае принадлежности случайного вектора многомерному
распределению Стьюдента статистика ![]() хорошо описывается классическим
хорошо описывается классическим ![]() распределением,
что отображено на рисунке 3.8.
распределением,
что отображено на рисунке 3.8.
При малых значениях степеней свободы ![]() распределения статистик
распределения статистик ![]() и
и ![]() претерпевают незначительные
изменения, что сказывается на достигаемых уровнях значимости по критериям
согласия. Предположительно, такое изменение распределений статистик обусловлено
<<утяжелением хвостов>> распределения Стьюдента. При
претерпевают незначительные
изменения, что сказывается на достигаемых уровнях значимости по критериям
согласия. Предположительно, такое изменение распределений статистик обусловлено
<<утяжелением хвостов>> распределения Стьюдента. При ![]() распределение
Стьюдента представляет собой распределение Коши. А ранее уже отмечалось
изменение предельных распределений статистик
распределение
Стьюдента представляет собой распределение Коши. А ранее уже отмечалось
изменение предельных распределений статистик ![]() и
и ![]() при многомерных законах, построенных
по семейству распределений (6.4) с параметром формы
при многомерных законах, построенных
по семейству распределений (6.4) с параметром формы ![]() .
.
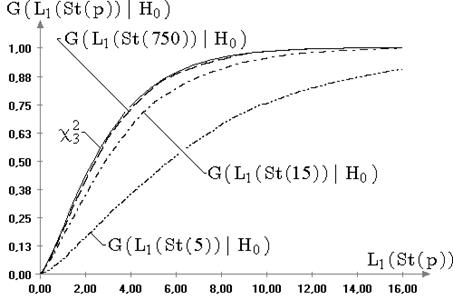
Рис. 3.9. Эмпирические распределения статистики ![]() , построенной по многомерному
закону Стьюдента с числами степеней свободы
, построенной по многомерному
закону Стьюдента с числами степеней свободы ![]() ,
, ![]() и
и ![]() , и классическое предельное
, и классическое предельное ![]() "– распределение (
"– распределение (![]() ,
, ![]() )
)
Полученные результаты для многомерного распределения Стьюдента не
опровергают ранее сделанных предположений об устойчивости критериев проверки
гипотез о векторе математических ожиданий к отклонению наблюдаемого
многомерного закона от нормального. Распределения статистик критериев проверки
гипотез о ковариационной матрице, как и ожидалось, сильно зависят от вида
многомерного закона. Поэтому распределения статистик ![]() и
и ![]() стремятся к классическим
предельным только при очень больших значениях числа степеней свободы
стремятся к классическим
предельным только при очень больших значениях числа степеней свободы ![]() (когда
распределение Стьюдента по виду очень близко к нормальному закону). В качестве
примера на рисунке 3.9 показано, что распределение статистики
(когда
распределение Стьюдента по виду очень близко к нормальному закону). В качестве
примера на рисунке 3.9 показано, что распределение статистики ![]() , моделируемой по
двумерному закону Стьюдента при очень большом значении числа степеней свободы
, моделируемой по
двумерному закону Стьюдента при очень большом значении числа степеней свободы ![]() , уже достаточно
хорошо описывается предельным классическим
, уже достаточно
хорошо описывается предельным классическим ![]() – распределением
статистики (3.3).
– распределением
статистики (3.3).
3.4. Уточнение моделей распределений статистик рассматриваемых критериев
Как показано выше, распределения статистик, используемых в критериях
проверки гипотез о векторе математических ожиданий, при существенном отличии
наблюдаемого закона от нормального незначимо отличаются от предельных
распределений, полученных в классическом случае. Результаты моделирования
распределений статистик ![]() и
и ![]() в случае принадлежности многомерных
величин законам, отличающимся от нормального, показали, что эмпирические
распределения статистик очень хорошо согласуются с предельными законами,
полученными в предположении о нормальности многомерного случайного вектора. Нет
оснований для отказа от использования в качестве предельных в соответствующих
случаях распределений
в случае принадлежности многомерных
величин законам, отличающимся от нормального, показали, что эмпирические
распределения статистик очень хорошо согласуются с предельными законами,
полученными в предположении о нормальности многомерного случайного вектора. Нет
оснований для отказа от использования в качестве предельных в соответствующих
случаях распределений ![]() или Фишера.
или Фишера.
Распределение ![]() представляет собой частный случай
гамма – распределения, F – распределение Фишера — частный случай бета
– распределения 2-го рода. Если, например, действительно
представляет собой частный случай
гамма – распределения, F – распределение Фишера — частный случай бета
– распределения 2-го рода. Если, например, действительно ![]() – распределение
является предельным распределением некоторой статистики и в том случае, когда
нарушается предположение о нормальности наблюдаемой многомерной величины, а мы
для выравнивания эмпирического распределения статистики каждый раз будем
использовать гамма – распределение, оценивая его параметры по выборке
статистики, то модель гамма – распределения с параметрами, полученными усреднением
по множеству экспериментов, должна привести нас к соответствующему
– распределение
является предельным распределением некоторой статистики и в том случае, когда
нарушается предположение о нормальности наблюдаемой многомерной величины, а мы
для выравнивания эмпирического распределения статистики каждый раз будем
использовать гамма – распределение, оценивая его параметры по выборке
статистики, то модель гамма – распределения с параметрами, полученными усреднением
по множеству экспериментов, должна привести нас к соответствующему ![]() – распределению.
– распределению.
Исходя из вышесказанного, мы попытались уточнить модели
распределений статистик ![]() и
и ![]() следующим образом. Моделировалась
выборка интересующей нас статистики, как правило, объемом в
следующим образом. Моделировалась
выборка интересующей нас статистики, как правило, объемом в ![]() наблюдений. Эмпирическое
распределение статистики сглаживалось соответствующей моделью (гамма
– распределением, бета – распределением) с оцениванием ее параметров.
Такой эксперимент повторялся несколько десятков раз. Параметры моделей
усреднялись по всей совокупности экспериментов. Если вид модели соответствует
предельному распределению статистики, то среднее арифметическое вектора параметров
модели должно сходиться к истинному значению вектора параметров. Например, от
модели гамма"– распределения будем приходить в соответствующем случае
к ее частному случаю
наблюдений. Эмпирическое
распределение статистики сглаживалось соответствующей моделью (гамма
– распределением, бета – распределением) с оцениванием ее параметров.
Такой эксперимент повторялся несколько десятков раз. Параметры моделей
усреднялись по всей совокупности экспериментов. Если вид модели соответствует
предельному распределению статистики, то среднее арифметическое вектора параметров
модели должно сходиться к истинному значению вектора параметров. Например, от
модели гамма"– распределения будем приходить в соответствующем случае
к ее частному случаю ![]() "– распределению.
"– распределению.
Предельным распределением классической статистики ![]() является
является ![]() "– распределение (3.1),
где
"– распределение (3.1),
где ![]() "—
размерность многомерного вектора. Это соответствует гамма"– распределению
с плотностью
"—
размерность многомерного вектора. Это соответствует гамма"– распределению
с плотностью
![]() (3.5)
(3.5)
с параметром формы ![]() и параметром масштаба
и параметром масштаба ![]() .
.
Таблица 3.1. Оценки параметров выравнивающего
гамма"– распределения для статистики ![]() , построенной по многомерным
законам с различными
, построенной по многомерным
законам с различными ![]() (
(![]() )
)
|
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.2. Оценки параметров выравнивающего
бета"– распределения для статистики ![]() , построенной по многомерным
законам с различными
, построенной по многомерным
законам с различными ![]() (
(![]() и
и ![]() )
)
|
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице 3.1 представлены усредненные по 50 смоделированным
выборкам статистики ![]() значения параметров модели
гамма"– распределения, аппроксимирующего распределение статистики в
случае законов многомерных величин, моделируемых при различных значениях
параметра датчика
значения параметров модели
гамма"– распределения, аппроксимирующего распределение статистики в
случае законов многомерных величин, моделируемых при различных значениях
параметра датчика ![]() (
(![]() соответствует нормальному закону).
В данном примере размерность моделируемых многомерных величин
соответствует нормальному закону).
В данном примере размерность моделируемых многомерных величин ![]() . Напомним, что
значимого влияния размерности
. Напомним, что
значимого влияния размерности ![]() на сходимость распределения
статистики
на сходимость распределения
статистики ![]() к
предельному выявлено не было. Очевидно, что значения параметров в случае
наблюдения нормального закона сходятся к значениям
к
предельному выявлено не было. Очевидно, что значения параметров в случае
наблюдения нормального закона сходятся к значениям ![]() и
и ![]() соответственно, что
соответствует
соответственно, что
соответствует ![]() "– распределению.
По крайней мере, нет оснований для отклонения данного предположения.
"– распределению.
По крайней мере, нет оснований для отклонения данного предположения.
При проверке аналогичной гипотезы при неизвестной ковариационной
матрице предельным распределение статистики ![]() является
является ![]() – распределение.
Данному случаю соответствует бета– распределение 2-го рода, плотность
которого имеет вид
– распределение.
Данному случаю соответствует бета– распределение 2-го рода, плотность
которого имеет вид
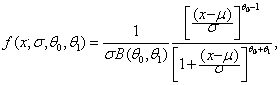 (3.6)
(3.6)
с масштабным параметром ![]() , параметрами формы
, параметрами формы ![]() и
и ![]() .
.
Представленные в таблице 3.2 усредненные по 50 смоделированным
выборкам статистики ![]() значения параметров
бета– распределения (при
значения параметров
бета– распределения (при ![]() и
и ![]() ) показывают аналогичную картину
сходимости. Очевидно, что значения параметров бета– распределения в случае
наблюдения нормального закона сходятся к значениям
) показывают аналогичную картину
сходимости. Очевидно, что значения параметров бета– распределения в случае
наблюдения нормального закона сходятся к значениям ![]() ,
, ![]() ,
, ![]() , что соответствует
F"– распределению Фишера с числом степеней свободы 3 и 27.
, что соответствует
F"– распределению Фишера с числом степеней свободы 3 и 27.
Таким образом, уточнение моделей распределений статистик ![]() и
и ![]() еще раз подтверждает
предположение об устойчивости соответствующих критериев к отклонению от
нормальности.
еще раз подтверждает
предположение об устойчивости соответствующих критериев к отклонению от
нормальности.
Таблица 3.3. Оценки параметров гамма – распределений,
используемых в качестве моделей распределений статистики ![]() , построенной по многомерным
законам с различными
, построенной по многомерным
законам с различными ![]()
|
|
|
|
|
|
|
|||||
|
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
4.21 |
1.46 |
2.00 |
1.50 |
1.68 |
1.49 |
1.45 |
1.50 |
1.48 |
1.43 |
|
|
3.83 |
2.71 |
2.00 |
3.00 |
1.74 |
2.97 |
1.70 |
2.85 |
1.69 |
2.77 |
|
|
3.58 |
4.43 |
2.00 |
5.00 |
1.80 |
4.99 |
1.78 |
4.84 |
1.75 |
4.80 |
|
|
- |
- |
2.00 |
7.50 |
1.84 |
7.50 |
1.87 |
7.08 |
1.85 |
7.00 |
Таблица 3.4. Оценки параметров гамма – распределений,
используемых в качестве моделей распределений статистики ![]() , построенной по многомерным
законам с различными
, построенной по многомерным
законам с различными ![]()
|
|
|
|
|
|
|
|||||
|
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
3.53 |
2.25 |
2.00 |
2.50 |
1.80 |
2.46 |
1.73 |
2.42 |
1.72 |
2.40 |
|
|
3.36 |
3.99 |
2.00 |
4.50 |
1.87 |
4.38 |
1.81 |
4.36 |
1.83 |
4.20 |
|
|
3.31 |
6.05 |
2.00 |
7.00 |
1.86 |
7.02 |
1.89 |
6.66 |
1.84 |
6.72 |
|
|
3.22 |
8.55 |
2.00 |
9.00 |
1.92 |
9.80 |
1.99 |
9.26 |
1.99 |
9.10 |
В случае статистик ![]() и
и ![]() , которые используются при проверке
гипотез о ковариационной матрице, видна явная зависимость распределений данных
статистик от вида наблюдаемого многомерного закона. Поэтому для распределений
статистик
, которые используются при проверке
гипотез о ковариационной матрице, видна явная зависимость распределений данных
статистик от вида наблюдаемого многомерного закона. Поэтому для распределений
статистик ![]() и
и
![]() постарались
найти подходящие аналитические модели законов. К сожалению, как и в одномерном
случае [76,77], нам не удалось построить модели распределений данных статистик
с параметрами, зависящими от
постарались
найти подходящие аналитические модели законов. К сожалению, как и в одномерном
случае [76,77], нам не удалось построить модели распределений данных статистик
с параметрами, зависящими от ![]() . Поэтому на основании результатов
статистического моделирования были найдены оценки параметров моделей законов,
которые наилучшим образом (по критериям согласия) подходят для описания
эмпирических распределений данных статистик. Оценки параметров распределений
находились по выборкам значений статистик
. Поэтому на основании результатов
статистического моделирования были найдены оценки параметров моделей законов,
которые наилучшим образом (по критериям согласия) подходят для описания
эмпирических распределений данных статистик. Оценки параметров распределений
находились по выборкам значений статистик ![]() и
и ![]() достаточно больших объемов (
достаточно больших объемов (![]() ), а затем
усреднялись по ряду экспериментов.
), а затем
усреднялись по ряду экспериментов.
Полученные оценки параметров гамма"– распределений,
которые оказались наилучшими моделями для распределений статистик ![]() и
и ![]() при значениях
параметра формы
при значениях
параметра формы ![]() , равном 1, 3, 4 и 5, приведены в
таблицах 3.3 и 3.4 соответственно. Значения параметров
гамма"– распределения при
, равном 1, 3, 4 и 5, приведены в
таблицах 3.3 и 3.4 соответственно. Значения параметров
гамма"– распределения при ![]() , приведенные в таблицах,
соответствуют предельным распределениям статистик при нормальном законе наблюдаемых
величин.
, приведенные в таблицах,
соответствуют предельным распределениям статистик при нормальном законе наблюдаемых
величин.
Если наблюдается многомерный закон, отличный от нормального, а
маргинальные функции плотности данного закона хорошо описываются семейством
распределений (6.4), тогда при помощи таблиц 3.3 и 3.4 можно подобрать
наилучшую модель для распределений статистик ![]() и
и ![]() . Например, если в двумерном случае
ковариационная матрица имеет диагональный вид, а маргинальные функции
распределения описываются семейством распределений (6.4) при параметре
формы равным 1, тогда в качестве предельного закона распределения статистики
. Например, если в двумерном случае
ковариационная матрица имеет диагональный вид, а маргинальные функции
распределения описываются семейством распределений (6.4) при параметре
формы равным 1, тогда в качестве предельного закона распределения статистики ![]() можно
использовать гамма – распределение с параметрами
можно
использовать гамма – распределение с параметрами ![]() и
и ![]() .
.
3.5. Выводы
Исследования эмпирических распределений статистик, используемых в критериях проверки гипотез о векторе математических ожиданий и ковариационной матрице, при псевдослучайных величинах, подчиняющихся многомерному нормальному закону, показали, что они хорошо согласуются с теоретическими предельными распределениями, полученными в классическом корреляционном анализе, и подтвердили эффективность методики исследований.
Исследования распределений статистик ![]() и
и ![]() в случае многомерных законов,
отличающихся от нормального в достаточно широких пределах (более островершинных
или более плосковершинных), показали, что значимого изменения предельных
распределений статистик не происходит. Эмпирические распределения данных
статистик по-прежнему хорошо описываются предельными законами, полученными в
классическом корреляционном анализе в предположении о нормальности наблюдаемого
вектора. Это существенно расширяет сферу корректного применения методов
классического корреляционного анализа при проверке гипотез о векторе
математических ожиданий в приложениях. Аналогичная ситуация наблюдается в одномерном
случае: на распределениях статистик, вычисляемых при проверке гипотез вида
в случае многомерных законов,
отличающихся от нормального в достаточно широких пределах (более островершинных
или более плосковершинных), показали, что значимого изменения предельных
распределений статистик не происходит. Эмпирические распределения данных
статистик по-прежнему хорошо описываются предельными законами, полученными в
классическом корреляционном анализе в предположении о нормальности наблюдаемого
вектора. Это существенно расширяет сферу корректного применения методов
классического корреляционного анализа при проверке гипотез о векторе
математических ожиданий в приложениях. Аналогичная ситуация наблюдается в одномерном
случае: на распределениях статистик, вычисляемых при проверке гипотез вида ![]() при известной и
неизвестной дисперсии, отклонения от нормальности наблюдаемого одномерного
закона сказываются незначительно.
при известной и
неизвестной дисперсии, отклонения от нормальности наблюдаемого одномерного
закона сказываются незначительно.
Используемые в критериях проверки гипотез о ковариационной матрице
многомерного закона статистики ![]() и
и ![]() существенно зависят от наблюдаемого
многомерного закона, что и подтвердили проведенные исследования. Это
согласуется с полученными результатами при моделировании распределений аналогичных
статистик в одномерном случае (при проверке гипотез вида
существенно зависят от наблюдаемого
многомерного закона, что и подтвердили проведенные исследования. Это
согласуется с полученными результатами при моделировании распределений аналогичных
статистик в одномерном случае (при проверке гипотез вида ![]() при известном и неизвестном
математическом ожидании). Для распределений статистик
при известном и неизвестном
математическом ожидании). Для распределений статистик ![]() и
и ![]() были найдены
аналитические модели законов, описывающие распределения этих статистик при
определенных значениях размерности
были найдены
аналитические модели законов, описывающие распределения этих статистик при
определенных значениях размерности ![]() и параметре формы
и параметре формы ![]() . При
необходимости аналогичные аналитические модели могут быть построены для любых
интересующих нас значений параметров
. При
необходимости аналогичные аналитические модели могут быть построены для любых
интересующих нас значений параметров ![]() и
и ![]() .
.
4. Исследование критериев проверки гипотез о коэффициентах корреляции
В классическом корреляционном анализе на основании исследований парных, частных и множественных корреляций можно делать выводы о характере статистической зависимости. Когда требуется определить взаимозависимость двух величин, исследуется парная корреляция. В случае, если интересует взаимозависимость двух величин, когда устранено воздействие остальных величин, то исследуется, так называемая, частная корреляция. А когда требуется рассмотреть зависимость единственной величины от группы других, исследуют множественную корреляцию. В этой главе исследуется устойчивость критериев, используемых в задачах о выявлении характера статистической зависимости между двумя или большим числом случайных величин при наблюдении различных многомерных законов распределения [70, 71, 73–75, 79].
4.1. Классические критерии проверки гипотез о коэффициентах корреляции
4.1.1. Проверка гипотез о коэффициентах парной корреляции
Взаимозависимость двух компонент случайного вектора характеризуется
парным коэффициентом корреляции ![]() . Он представляет собой меру тесноты
линейной связи. Известно, что независимость двух случайных величин влечет
равенство
. Он представляет собой меру тесноты
линейной связи. Известно, что независимость двух случайных величин влечет
равенство ![]() ,
однако обратное утверждение в общем случае неверно. Что и представляет
трудность интерпретации
,
однако обратное утверждение в общем случае неверно. Что и представляет
трудность интерпретации ![]() как коэффициента взаимозависимости
в общем случае. Однако, оно справедливо для совместно нормальных величин.
Коэффициент корреляции можно использовать в качестве некоторой меры
взаимозависимости для нормального закона. Если известна оценка ковариационной
матрицы
как коэффициента взаимозависимости
в общем случае. Однако, оно справедливо для совместно нормальных величин.
Коэффициент корреляции можно использовать в качестве некоторой меры
взаимозависимости для нормального закона. Если известна оценка ковариационной
матрицы ![]() ,
то оценка парного коэффициента корреляции может быть найдена в соответствии с
выражением
,
то оценка парного коэффициента корреляции может быть найдена в соответствии с
выражением
![]() (4.1)
(4.1)
В классическом корреляционном анализе относительно парного
коэффициента корреляции могут проверяться два вида гипотез: о значимости коэффициента
корреляции (![]() )
и о равенстве его номинальному значению (
)
и о равенстве его номинальному значению (![]() ).
).
В критерии проверки гипотезы ![]() используется статистика
используется статистика
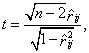 (4.2)
(4.2)
которая при справедливости гипотезы ![]() имеет в качестве предельного
распределение Стьюдента с
имеет в качестве предельного
распределение Стьюдента с ![]() степенями свободы:
степенями свободы: ![]() [33].
[33].
В случае проверки гипотезы ![]() вычисляется статистика
вычисляется статистика
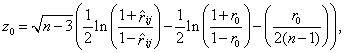 (4.3)
(4.3)
которая при справедливости гипотезы ![]() в качестве предельного
распределения
в качестве предельного
распределения ![]() имеет
стандартный нормальный закон
имеет
стандартный нормальный закон ![]() [33].
[33].
В [58] выдвинуто предположение о том, что критерий
некоррелированности (![]() ) можно строить без каких-либо
предположений о нормальности исходного распределения.
) можно строить без каких-либо
предположений о нормальности исходного распределения.
Известно, что оценка для ![]() является смещенной, когда
является смещенной, когда ![]() , что видно из выражения
[58]
, что видно из выражения
[58]
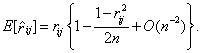
Олкин и Прэтт [58] рекомендуют использовать несмещенную оценку в виде
![]() . (4.4)
. (4.4)
4.1.2. Проверка гипотез о коэффициентах частной корреляции
Как ранее отмечалось, в случае двух нормальных или почти нормальных величин коэффициент корреляции между ними может быть использован в качестве меры взаимозависимости. Однако на практике при интерпретации <<взаимозависимости>> часто сталкиваются с трудностями, заключающимися в том, что, если одна величина коррелирована с другой, то это может быть всего лишь отражением того факта, что обе они коррелированы с некоторой третьей величиной или с совокупностью величин. Указанная возможность приводит к необходимости рассмотрения условных корреляций между двумя величинами при фиксированных значениях остальных величин. Это так называемые частные корреляции.
Если корреляция между двумя величинами уменьшается при фиксировании некоторой другой случайной величины, то это означает, что их взаимозависимость возникает частично через воздействие этой величины. Если же частная корреляция равна нулю или очень мала, то делается вывод, что их взаимозависимость целиком обусловлена этим воздействием. Наоборот, когда частная корреляция больше первоначальной корреляции между двумя величинами, то следует, что другие величины ослабляли связь, или, можно сказать, <<маскировали>> корреляцию. Но следует помнить, что даже в последнем случае нельзя предполагать наличие причинной связи, так как некоторая, совершенно отличная от рассматриваемых при анализе, величина может быть источником этой корреляции. Как при обычной корреляции, так и при частных корреляциях предположение о причинности должно всегда иметь внестатистические основания.
Представим случайный вектор ![]() в следующем виде [33]:
в следующем виде [33]:
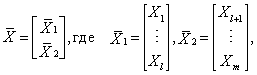
а вектор математических ожиданий и ковариационную матрицу соответственно в виде
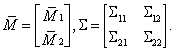
Тогда если случайный вектор ![]() подчиняется нормальному закону с
вектором средних
подчиняется нормальному закону с
вектором средних ![]() и ковариационной матрицей
и ковариационной матрицей ![]() , то условное
распределение подвектора
, то условное
распределение подвектора ![]() при известном
при известном ![]() является нормальным с
математическим ожиданием
является нормальным с
математическим ожиданием ![]() и ковариационной матрицей
и ковариационной матрицей ![]() , где
, где ![]() ,
, ![]() [58].
[58].
ОМП для частного коэффициента корреляции определяется соотношением:
![]() (4.5)
(4.5)
где ![]() —
элемент
—
элемент ![]() -й
строки и
-й
строки и ![]() -го
столбца матрицы
-го
столбца матрицы ![]() ,
, ![]() — число компонент в условном
распределении,
— число компонент в условном
распределении, ![]() .
В данном случае при оценке взаимозависимости между компонентами
.
В данном случае при оценке взаимозависимости между компонентами ![]() и
и ![]() случайной
величины
случайной
величины ![]() исключается
влияние компонент
исключается
влияние компонент ![]() .
.
При проверке гипотез относительно частных коэффициентов корреляции
вида ![]() и
и
![]() используются
те же самые статистики, что и для парного коэффициента корреляции. Но в данном
случае в соответствующих соотношениях
используются
те же самые статистики, что и для парного коэффициента корреляции. Но в данном
случае в соответствующих соотношениях ![]() заменяется на
заменяется на ![]() .
.
В критерии проверки гипотезы ![]() используется статистика
используется статистика
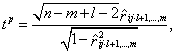 (4.6)
(4.6)
которая при справедливой гипотезе ![]() имеет в качестве предельного
распределение Стьюдента с
имеет в качестве предельного
распределение Стьюдента с ![]() степенями свободы:
степенями свободы: ![]() [33,58].
[33,58].
В случае проверки гипотезы ![]() вычисляемая статистика
вычисляемая статистика
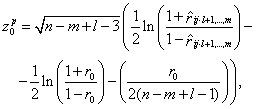 (4.7)
(4.7)
при справедливой гипотезе ![]() в качестве предельного
распределения
в качестве предельного
распределения ![]() имеет
стандартное нормальное распределение
имеет
стандартное нормальное распределение ![]() [33,58].
[33,58].
4.1.3. Проверка гипотезы о коэффициенте множественной корреляции
Множественный коэффициент корреляции является мерой зависимости компоненты многомерной случайной величины от некоторого множества компонент. Можно рассматривать корреляцию между одной компонентой случайного вектора и множеством всех остальных или каким-то подмножеством.
Следует отметить, что множественный коэффициент корреляции ![]() случайной
величины
случайной
величины ![]() относительно
некоторого множества других случайных величин всегда не меньше, чем абсолютная
величина любого парного коэффициента корреляции
относительно
некоторого множества других случайных величин всегда не меньше, чем абсолютная
величина любого парного коэффициента корреляции ![]() с таким же первичным индексом.
Более того, множественный коэффициент корреляции никогда нельзя уменьшить путем
расширения множества величин, относительно которых измеряется зависимость
с таким же первичным индексом.
Более того, множественный коэффициент корреляции никогда нельзя уменьшить путем
расширения множества величин, относительно которых измеряется зависимость ![]() .
.
Если коэффициент корреляции между ![]() и множеством всех остальных
компонент многомерной случайной величины равен нулю (
и множеством всех остальных
компонент многомерной случайной величины равен нулю (![]() ), то все коэффициенты
корреляции этой величины относительного любого подмножества также равны
), то все коэффициенты
корреляции этой величины относительного любого подмножества также равны ![]() , т.е. величина
, т.е. величина ![]() полностью
некоррелирована со всеми остальными величинами.
полностью
некоррелирована со всеми остальными величинами.
С другой стороны, если ![]() относительно множества всех
остальных компонент равен единице
относительно множества всех
остальных компонент равен единице ![]() , то, по крайней мере, один из
коэффициентов корреляции относительно некоторого подмножества компонент должен
быть равен 1.
, то, по крайней мере, один из
коэффициентов корреляции относительно некоторого подмножества компонент должен
быть равен 1.
Надо отметить, что коэффициент корреляции, например, между ![]() и множеством
всех остальных компонент является обычным коэффициентом корреляции между
и множеством
всех остальных компонент является обычным коэффициентом корреляции между ![]() и условным
математическим ожиданием
и условным
математическим ожиданием ![]() .
.
С учетом выше рассмотренного разбиения случайного вектора ![]() ОМП множественного
коэффициента корреляции между
ОМП множественного
коэффициента корреляции между ![]() и множеством компонент
и множеством компонент ![]() определяется
соотношением
определяется
соотношением
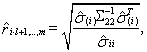 (4.8)
(4.8)
где ![]() —
i-ая строка матрицы
—
i-ая строка матрицы ![]() ,
, ![]() — элемент матрицы
— элемент матрицы ![]() .
.
Для проверки гипотезы о значимости множественного коэффициента
корреляции ![]() вычисляется
статистика
вычисляется
статистика
![]() (4.9)
(4.9)
предельным распределением ![]() которой является
которой является ![]() — распределение
Фишера с параметрами
— распределение
Фишера с параметрами ![]() и
и ![]() [33,58].
[33,58].
4.2. Исследование распределений статистик критериев для различных многомерных законов
4.2.1. В случае принадлежности наблюдений многомерному нормальному закону
Как и ранее в первую очередь при помощи статистического моделирования нами исследовались распределения статистик, используемых при проверке гипотез о различных коэффициентах корреляции, на подчиненность соответствующим предельным распределениям в случае многомерного нормального закона. Проведенные экспериментальные исследования подтвердили хорошее согласие между получаемыми эмпирическими распределениями статистик критериев о коэффициентах корреляции и соответствующими предельными законами.
В процессе исследования сходимости распределений статистик к
предельным в зависимости от объема выборки ![]() нами были оценены объемы выборок
нормальных псевдослучайных векторов, начиная с которых наблюдается близость
эмпирической и теоретической функций распределений статистик. Так, у статистик
нами были оценены объемы выборок
нормальных псевдослучайных векторов, начиная с которых наблюдается близость
эмпирической и теоретической функций распределений статистик. Так, у статистик ![]() и
и ![]() высокий достигаемый
уровень значимости наблюдается, начиная с объемов выборки
высокий достигаемый
уровень значимости наблюдается, начиная с объемов выборки ![]() , а для статистик
, а для статистик ![]() ,
, ![]() и
и ![]() — с
— с ![]() (следствие
зависимости предельных распределений данных статистик от
(следствие
зависимости предельных распределений данных статистик от ![]() ).
).
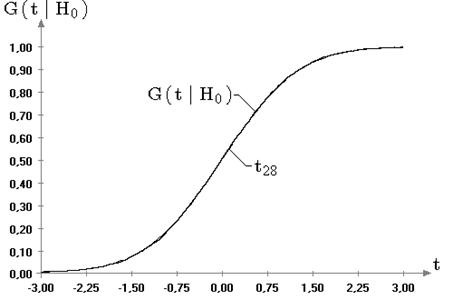
Рис. 4.1. Эмпирическая и теоретическая функции распределения
статистики ![]() (4.2) при проверке гипотезы
(4.2) при проверке гипотезы
![]() , построенная с
использованием параметров моделирования (4.10):
, построенная с
использованием параметров моделирования (4.10): ![]()
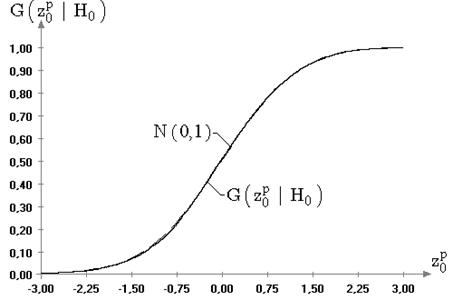
Рис. 4.2. Эмпирическая и теоретическая функции
распределения статистики ![]() (4.7)
при проверке гипотезы
(4.7)
при проверке гипотезы ![]() ,
построенной с использованием параметров моделирования (4.10):
,
построенной с использованием параметров моделирования (4.10): ![]()
Продемонстрируем сказанное на двух примерах, со следующими наборами параметров моделирования
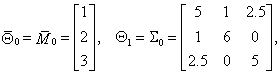 (4.10)
(4.10)
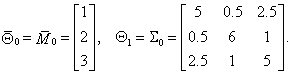 (4.11)
(4.11)
На рисунке 4.1 приведены в качестве примера полученная в
результате моделирования эмпирическая и теоретическая функции распределения
статистики ![]() (4.2),
используемой при проверке гипотезы о незначимости парного коэффициента
корреляции (
(4.2),
используемой при проверке гипотезы о незначимости парного коэффициента
корреляции (![]() ).
В данном случае при моделировании использовались следующие значения параметров:
).
В данном случае при моделировании использовались следующие значения параметров:
![]() ,
, ![]() , а
, а ![]() и
и ![]() из (1). На
основании достигнутых уровней значимости критериев согласия, приведенных на
рисунке, и визуальной близости эмпирической и теоретической функций
распределения статистики
из (1). На
основании достигнутых уровней значимости критериев согласия, приведенных на
рисунке, и визуальной близости эмпирической и теоретической функций
распределения статистики ![]() можно судить о достаточности объемов
выборок
можно судить о достаточности объемов
выборок ![]() случайных
векторов для приемлемого согласия. Аналогичная картина наблюдается и при
моделировании распределений статистики
случайных
векторов для приемлемого согласия. Аналогичная картина наблюдается и при
моделировании распределений статистики ![]() (4.6).
(4.6).
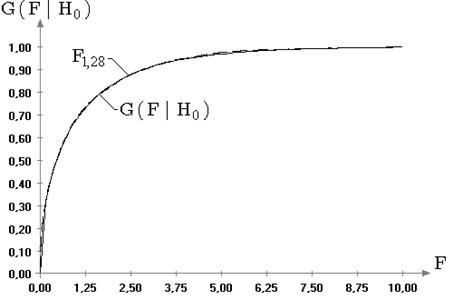
Рис. 4.3. Эмпирическая и теоретическая функции
распределения статистики ![]() (4.9)
при проверке гипотезы
(4.9)
при проверке гипотезы ![]() ,
построенная с использованием параметров моделирования (4.10):
,
построенная с использованием параметров моделирования (4.10): ![]()
Пример на рис. 4.2 демонстрирует близость между распределениями
статистики ![]() (4.7),
построенными для многомерного нормального закона при моделировании с параметрами
(4.7),
построенными для многомерного нормального закона при моделировании с параметрами
![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() (4.11). Вновь
наблюдается высокий достигаемый уровень значимости при проверке согласия между
эмпирическим и теоретическим распределениями используемой статистики, начиная с
объемов выборок
(4.11). Вновь
наблюдается высокий достигаемый уровень значимости при проверке согласия между
эмпирическим и теоретическим распределениями используемой статистики, начиная с
объемов выборок ![]() . Полученные результаты
моделирования статистики
. Полученные результаты
моделирования статистики ![]() подтверждают общую картину, полученную
при исследовании статистики
подтверждают общую картину, полученную
при исследовании статистики ![]() .
.
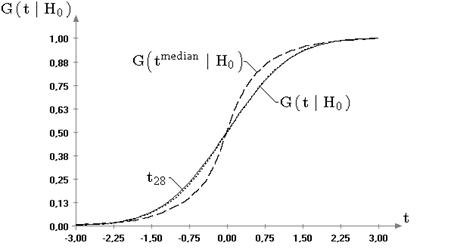
Рис. 4.4. Эмпирические и теоретическая функции
распределения статистики ![]() (4.2)
при проверке гипотезы
(4.2)
при проверке гипотезы ![]() ,
построенных с использованием оценок парного коэффициента корреляции по формулам (4.1)
и (4.12):
,
построенных с использованием оценок парного коэффициента корреляции по формулам (4.1)
и (4.12): ![]()
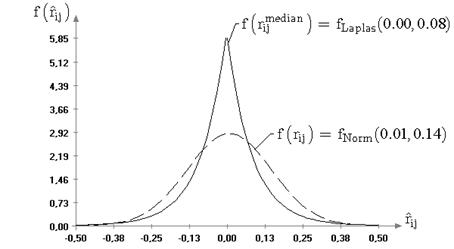
Рис. 4.5. Функции плотности оценок парного коэффициента корреляции, вычисляемого по формулам (4.1) и (4.12)
По результатам исследования распределений статистики ![]() (4.9),
используемой при проверке гипотезы о равенстве множественного коэффициента
корреляции нулевому значению, моделируемых, например, с параметрами
(4.9),
используемой при проверке гипотезы о равенстве множественного коэффициента
корреляции нулевому значению, моделируемых, например, с параметрами ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() (4.10), можно
говорить о <<достаточности>> объемов выборок случайных векторов,
начиная с
(4.10), можно
говорить о <<достаточности>> объемов выборок случайных векторов,
начиная с ![]() .
Результаты описанного эксперимента приведены на рис. 4.3.
.
Результаты описанного эксперимента приведены на рис. 4.3.
Отметим, что при исследовании вновь не было выявлено существенного
влияния размерности случайного вектора ![]() и на сходимость распределений
статистик данных критериев к соответствующим классическим предельным.
и на сходимость распределений
статистик данных критериев к соответствующим классическим предельным.
В работе [103] показано, что оценка парного коэффициента корреляции по формуле (4.1) не является устойчивой по отношению к нарушению предположения о нормальности распределения, из которого получена выборка для вычисления оценки. Различные робастные аналоги оценки коэффициента приведены во многих работах [1,7,20,21,42,102]. Например, одна из таких оценок имеет вид
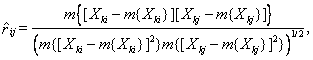 (4.12)
(4.12)
где ![]() —
медиана псевдослучайных величин
—
медиана псевдослучайных величин ![]() .
.
Если использовать оценку (4.12) в статистике ![]() (4.2), то
наблюдается явное изменение предельного распределения статистики, что отражено
на рисунке 4.4. Такое изменение объясняется тем, что функция плотности
распределения оценки (4.12) становится более
<<островершинной>> (следствие робастности оценки). На
рисунке 4.5 приведены функции плотности распределения оценок
(4.2), то
наблюдается явное изменение предельного распределения статистики, что отражено
на рисунке 4.4. Такое изменение объясняется тем, что функция плотности
распределения оценки (4.12) становится более
<<островершинной>> (следствие робастности оценки). На
рисунке 4.5 приведены функции плотности распределения оценок ![]() при
при ![]() , полученные в
результате моделирования. Где для распределения оценки, вычисленной по
формуле (4.1), лучше всего подходит нормальный закон с соответствующими
параметрами сдвига и масштаба
, полученные в
результате моделирования. Где для распределения оценки, вычисленной по
формуле (4.1), лучше всего подходит нормальный закон с соответствующими
параметрами сдвига и масштаба ![]() , а для оценки (4.12) —
распределение Лапласа
, а для оценки (4.12) —
распределение Лапласа ![]() . Это различие в распределениях
оценок коэффициента парной корреляции и приводит к существенному уменьшению
размаха предельного распределения статистики
. Это различие в распределениях
оценок коэффициента парной корреляции и приводит к существенному уменьшению
размаха предельного распределения статистики ![]() (см. рис. 4.4).
(см. рис. 4.4).
Отсюда следует, что применяя критерии проверки гипотез о парном коэффициенте корреляции, следует использовать оценки по методам, указанным при построении критериев: в данном случае — по методу максимального правдоподобия.
4.2.2. В случае принадлежности наблюдений многомерным законам, моделируемым на основе семейства симметричных распределений (6.4)
Распределения статистик, используемых в критериях проверки гипотез о
коэффициентах корреляции, исследовались при различных объемах выборок ![]() и различной
размерности случайных величин
и различной
размерности случайных величин ![]() на многомерных законах,
моделируемых с использованием предложенной в данной работе процедуры. Ранее отмечалось,
что в [58] выдвигалось предположение об устойчивости распределения статистики
на многомерных законах,
моделируемых с использованием предложенной в данной работе процедуры. Ранее отмечалось,
что в [58] выдвигалось предположение об устойчивости распределения статистики ![]() (4.2) (критерий
некоррелированности) к отклонениям от нормальности наблюдаемого закона. Там же
была показана явная зависимость распределения статистики
(4.2) (критерий
некоррелированности) к отклонениям от нормальности наблюдаемого закона. Там же
была показана явная зависимость распределения статистики ![]() (4.3) от вида
многомерного закона. Проверим эти предположения на моделируемых многомерных
законах.
(4.3) от вида
многомерного закона. Проверим эти предположения на моделируемых многомерных
законах.
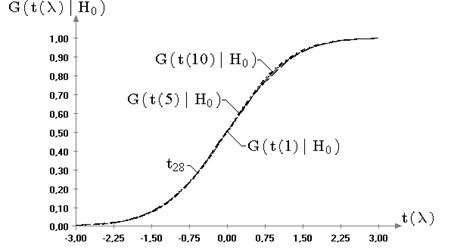
Рис. 4.6. Эмпирические распределения статистик ![]() ,
, ![]() ,
, ![]() и классическое предельное
и классическое предельное ![]() – распределение статистики
(4.2) при проверке гипотезы
– распределение статистики
(4.2) при проверке гипотезы ![]() , где
, где ![]() и (4.10)
и (4.10)
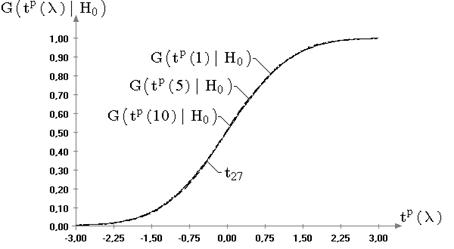
Рис. 4.7. Эмпирические распределения статистик ![]() ,
, ![]() ,
, ![]() и классическое предельное
и классическое предельное ![]() – распределение статистики
(4.6) при проверке гипотезы
– распределение статистики
(4.6) при проверке гипотезы ![]() , где
, где ![]() ,
, ![]() ,
, ![]() и (4.11)
и (4.11)
Приведем полученные в результате исследований примеры
смоделированных эмпирических распределений статистик с отражением близости их к
соответствующим предельным распределениям, полученным в предположении о
нормальности выборки. Количественной мерой близости служат достигаемые уровни
значимости по критериям согласия ![]() Пирсона, Колмогорова,
Пирсона, Колмогорова, ![]() и
и ![]() Мизеса. Чем
ближе достигнутый уровень значимости к 1, тем лучше согласие эмпирического
распределения с соответствующим теоретическим.
Мизеса. Чем
ближе достигнутый уровень значимости к 1, тем лучше согласие эмпирического
распределения с соответствующим теоретическим.
Из результатов приведенных на рисунках 4.6 и 4.7 следует, что нет
оснований для отклонения предположений о том, что предельными распределениями
статистик критериев проверки гипотез о равенстве парного и частного
коэффициентов корреляции нулевому значению при наблюдении многомерных законов,
построенных по одномерному закону из семейства распределений (6.4) при
разных параметрах формы ![]() , являются соответствующие
классические предельные распределения. Достигаемые уровни значимости по
критериям согласия для результатов, отраженных на данных рисунках, сведены в
таблицу 4.1. Результаты исследований показали, что распределения статистик
(4.2) и (4.6) устойчивы к отклонениям многомерного закона от нормального.
, являются соответствующие
классические предельные распределения. Достигаемые уровни значимости по
критериям согласия для результатов, отраженных на данных рисунках, сведены в
таблицу 4.1. Результаты исследований показали, что распределения статистик
(4.2) и (4.6) устойчивы к отклонениям многомерного закона от нормального.
Таблица 4.1. Значения достигнутых уровней значимости по
критериям согласия для распределений статистик ![]() ,
, ![]() и
и ![]() , смоделированных при
различных параметрах формы
, смоделированных при
различных параметрах формы ![]() ,
приведенных на рисунках 4.6, 4.7 и 4.8
,
приведенных на рисунках 4.6, 4.7 и 4.8
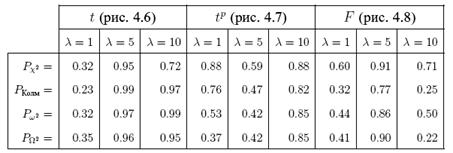
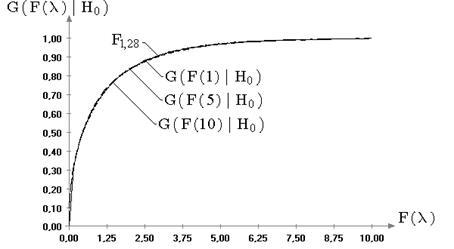
Рис. 4.8. Эмпирические распределения статистик ![]() ,
, ![]() ,
, ![]() и классическое предельное
и классическое предельное ![]() – распределение статистики
(4.9) при проверке гипотезы
– распределение статистики
(4.9) при проверке гипотезы ![]() , где
, где ![]() ,
, ![]() ,
, ![]() и (4.10)
и (4.10)
Статистика (4.9), используемая при проверке гипотезы о равенстве нулю множественного коэффициента корреляции, также оказалась нечувствительна к отклонениям многомерного закона от нормального (рис. 4.8, таб. 4.1).
Таким образом, проведенные численные исследования не опровергают выдвигаемого в [58] предположения об устойчивости критериев проверки гипотез о равенстве нулю парного коэффициента корреляции по отношению к нарушению основного предположения корреляционного анализа о нормальности многомерного закона. Исследования проводились на различных размерностях псевдослучайных векторов и большом количестве повторных экспериментов с целью исключения ошибок возможных отдельных экспериментов. Поэтому можно выдвинуть более широкое предположение о том, что критерии проверки гипотез о нулевых значениях парного, частного и множественного коэффициентов корреляции являются устойчивыми к отклонениям от нормальности.
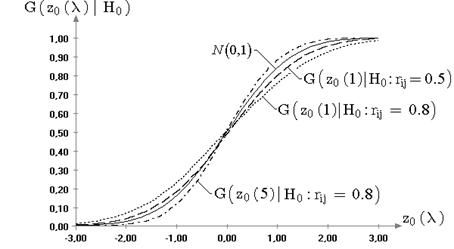
Рис. 4.9. Эмпирические распределения статистики ![]() , построенные для проверки
гипотез на равенство коэффициента парной корреляции различным значениям, и
классическое предельное
, построенные для проверки
гипотез на равенство коэффициента парной корреляции различным значениям, и
классическое предельное ![]() – распределение статистики (4.10)
– распределение статистики (4.10)
В критериях проверки гипотез о равенстве парного или частного коэффициента корреляции заданному значению распределения используемых статистик критериев очень чувствительны к виду наблюдаемого закона. Так, с ростом отклонения коэффициента корреляции от нулевого значения при прочих равных условиях происходит все более значимое отклонение распределения соответствующей статистики от классического предельного. Сказанное иллюстрирует рисунок 8, на котором показано, как с увеличением абсолютного значения коэффициента корреляции, изменяется распределение статистики данного критерия. В то время как в классическом случае распределение статистики в пределе стремится к стандартному нормальному распределению и не зависит от значения коэффициента корреляции.
На основании результатов исследований можно дать следующие
рекомендации. При законах, отличных от нормального, и малых значениях парного
(частного) коэффициента корреляции ![]() еще можно пользоваться стандартным
нормальным распределением как предельным для статистики
еще можно пользоваться стандартным
нормальным распределением как предельным для статистики ![]() (
(![]() ). Но при значениях
коэффициента корреляции
). Но при значениях
коэффициента корреляции ![]() требуется определение распределения
статистики используемого критерия.
требуется определение распределения
статистики используемого критерия.
Таблица 4.2. Значения
достигнутых уровней значимости по критериям согласия между ![]() – распределением и
распределением статистики
– распределением и
распределением статистики ![]() ,
смоделированной по многомерному закону Стьюдента при различных степенях свободы
,
смоделированной по многомерному закону Стьюдента при различных степенях свободы
![]() , усредненных по 3
экспериментам (
, усредненных по 3
экспериментам (![]() ,
, ![]() )
)
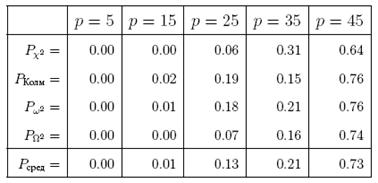
4.2.3. Случай принадлежности наблюдений многомерному закону Стьюдента
Исследования распределений статистик критериев проверки гипотез о
коэффициентах корреляции на многомерном распределении Стьюдента показало
ограниченность применения классических результатов для выборок, не
принадлежащих многомерному закону. Так, при наблюдении выборок, подчиняющихся
закону Стьюдента с числом степеней свободы ![]() , распределения статистик
, распределения статистик ![]() (42),
(42), ![]() (4.6) и
(4.6) и ![]() (4.9) не
сходятся к классическим предельным при объемах
(4.9) не
сходятся к классическим предельным при объемах ![]() , являющихся достаточными для нормального
закона. Это отражено на рисунках 4.10 и 4.11, где видно, что эмпирические
распределения данных статистик, полученные в результате моделирования
многомерных величин по закону Стьюдента с числом степеней свободы
, являющихся достаточными для нормального
закона. Это отражено на рисунках 4.10 и 4.11, где видно, что эмпирические
распределения данных статистик, полученные в результате моделирования
многомерных величин по закону Стьюдента с числом степеней свободы ![]() и
и ![]() , не подчиняются
соответствующим предельным распределениям для нормального случая. Значительное
увеличение объемов многомерных выборок
, не подчиняются
соответствующим предельным распределениям для нормального случая. Значительное
увеличение объемов многомерных выборок ![]() не улучшает сходимость распределений
статистик
не улучшает сходимость распределений
статистик ![]() ,
,
![]() и
и ![]() к классическим
предельным.
к классическим
предельным.
При дальнейшем увеличении параметра ![]() согласие между распределениями
данных статистик и соответствующими предельными законами в нормальном случае заметно
улучшается (см. рисунки 4.10, 4.11 и таблицу 4.2).
согласие между распределениями
данных статистик и соответствующими предельными законами в нормальном случае заметно
улучшается (см. рисунки 4.10, 4.11 и таблицу 4.2).
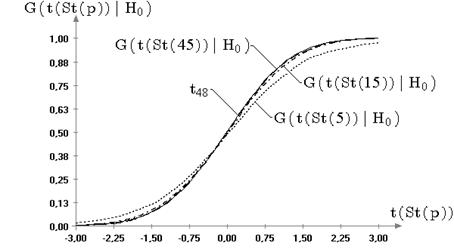
Рис. 4.10. Эмпирические распределения статистики ![]() , построенные по многомерному
распределению Стьюдента для
, построенные по многомерному
распределению Стьюдента для ![]() ,
, ![]() и
и ![]() числа степеней свободы, и
классическое предельное
числа степеней свободы, и
классическое предельное ![]() – распределение
статистики (4.2) при проверке гипотезы
– распределение
статистики (4.2) при проверке гипотезы ![]()
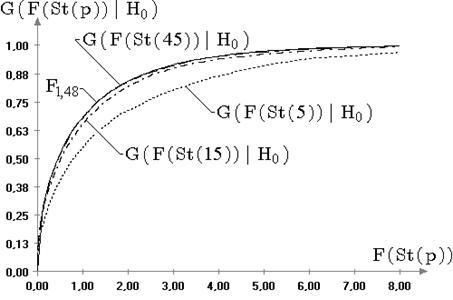
Рис. 4.11. Эмпирические распределения статистики ![]() , построенные по многомерному
распределению Стьюдента для
, построенные по многомерному
распределению Стьюдента для ![]() ,
, ![]() и
и ![]() числа степеней свободы, и
классическое предельное
числа степеней свободы, и
классическое предельное ![]() – распределение
статистики (4.9) при проверке гипотезы
– распределение
статистики (4.9) при проверке гипотезы ![]()
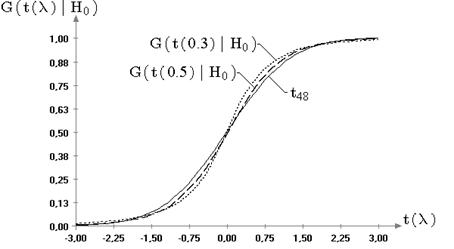
Рис. 4.12. Эмпирические распределения статистики ![]() ,
, ![]() , и классическое предельное
, и классическое предельное ![]() – распределение статистики
(4.2) при проверке гипотезы
– распределение статистики
(4.2) при проверке гипотезы ![]() , где
, где ![]() ,
, ![]()
Исследования распределений статистик критериев по выборкам
многомерного распределения, построенного по семейству распределений (6.4)
с параметром формы ![]() , демонстрируют аналогичные результаты,
что и в случае многомерного распределения Стьюдента с числом степеней свободы
, демонстрируют аналогичные результаты,
что и в случае многомерного распределения Стьюдента с числом степеней свободы ![]() : распределения
статистик
: распределения
статистик ![]() ,
,
![]() и
и ![]() претерпевают
изменения и более не подчиняются соответствующим предельным распределениям,
полученным в предположении о нормальности. Изменение предельного закона статистики
претерпевают
изменения и более не подчиняются соответствующим предельным распределениям,
полученным в предположении о нормальности. Изменение предельного закона статистики
![]() ,
моделируемой по семейству распределений (6.4) с параметрами формы
,
моделируемой по семейству распределений (6.4) с параметрами формы ![]() и
и ![]() , отражено на
рисунке 4.12.
, отражено на
рисунке 4.12.
Многомерные распределения Стьюдента при ![]() и многомерные
распределения, моделируемые на основе семейства распределений (6.4) с
параметром формы
и многомерные
распределения, моделируемые на основе семейства распределений (6.4) с
параметром формы ![]() , представляют собой законы с
<<тяжелыми хвостами>>. При
, представляют собой законы с
<<тяжелыми хвостами>>. При ![]() и
и ![]() в том и другом случае мы приходим к
многомерному распределению Коши.
в том и другом случае мы приходим к
многомерному распределению Коши.
Оценки максимального правдоподобия вектора математических ожиданий
и, особенно, ковариационных матриц (а, следовательно, и ОМП коэффициентов
корреляции) не являются робастными. Их асимптотические свойства резко
ухудшаются (увеличивается рассеяние) в случае многомерных законов при ![]() и
и ![]() . Этим объясняется
неустойчивость критериев проверки гипотез на нулевые значения коэффициентов
корреляции для многомерных законов, построенных с помощью соответствующих
процедур при
. Этим объясняется
неустойчивость критериев проверки гипотез на нулевые значения коэффициентов
корреляции для многомерных законов, построенных с помощью соответствующих
процедур при ![]() и
и
![]() , и
устойчивость этих же критериев для многомерных законов при
, и
устойчивость этих же критериев для многомерных законов при ![]() и
и ![]() .
.
4.3. Выводы
Исследования эмпирических распределений статистик, используемых в критериях проверки гипотез о парных, частных и множественных коэффициентах корреляции, при псевдослучайных величинах, подчиняющихся многомерному нормальному закону, показали, что они хорошо согласуются с теоретическими предельными распределениями, полученными в классическом корреляционном анализе. Отмечено существенное влияние метода вычисления оценок коэффициентов корреляции на распределения статистик данных критериев.
Исследования распределений статистик ![]() ,
, ![]() и
и ![]() в случае многомерных законов,
отличающихся от нормального в достаточно широких пределах, показали, что
значимого изменения предельных распределений статистик не происходит.
Эмпирические распределения данных статистик по-прежнему хорошо описываются
предельными законами, полученными в классическом корреляционном анализе в предположении
о нормальности наблюдаемого вектора. Это раздвигает границы корректного
применения методов классического корреляционного анализа при проверке гипотез о
нулевых значениях парного, частного и множественного коэффициентов корреляции.
в случае многомерных законов,
отличающихся от нормального в достаточно широких пределах, показали, что
значимого изменения предельных распределений статистик не происходит.
Эмпирические распределения данных статистик по-прежнему хорошо описываются
предельными законами, полученными в классическом корреляционном анализе в предположении
о нормальности наблюдаемого вектора. Это раздвигает границы корректного
применения методов классического корреляционного анализа при проверке гипотез о
нулевых значениях парного, частного и множественного коэффициентов корреляции.
В случае многомерных законов с <<тяжелыми хвостами>>
наблюдается значимое отличие распределений статистик ![]() ,
, ![]() и
и ![]() от предельных
классических.
от предельных
классических.
Используемые в критериях проверки гипотез о равенстве заданному
значению парного или частного коэффициента корреляции статистики ![]() и
и ![]() существенно
зависят от наблюдаемого многомерного закона. Это подтверждает выдвинутое в [58]
предположение о зависимости распределений данных статистик от вида многомерного
закона. В то же время классическими результатами можно пользоваться при
проверке гипотез вида
существенно
зависят от наблюдаемого многомерного закона. Это подтверждает выдвинутое в [58]
предположение о зависимости распределений данных статистик от вида многомерного
закона. В то же время классическими результатами можно пользоваться при
проверке гипотез вида ![]() , при
, при ![]() .
.
5. Исследование критериев проверки гипотез о корреляционном отношении
В классическом корреляционном анализе на основании соотношений между парным коэффициентом корреляции и корреляционным отношением можно судить о характере зависимости между компонентами случайного вектора.
5.1. Классические критерии проверки гипотез о корреляционном отношении
Корреляционное отношение случайной величины ![]() по
по ![]() определяется отношением
дисперсии условного математического ожидания
определяется отношением
дисперсии условного математического ожидания ![]() к дисперсии
к дисперсии ![]() :
:
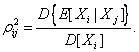 (5.1)
(5.1)
В отличие от коэффициента корреляции ![]() корреляционное отношение
корреляционное отношение ![]() несимметрично
относительно
несимметрично
относительно ![]() и
и
![]() .
Соотношение между коэффициентом корреляции
.
Соотношение между коэффициентом корреляции ![]() и корреляционным отношением
и корреляционным отношением ![]() в случае
многомерного нормального закона позволяет утверждать следующее[58]:
в случае
многомерного нормального закона позволяет утверждать следующее[58]:
·
![]() ,
если
,
если ![]() и
и
![]() независимы;
независимы;
·
![]() ,
тогда и только тогда, когда имеется строгая линейная функциональная зависимость
,
тогда и только тогда, когда имеется строгая линейная функциональная зависимость
![]() от
от ![]() ;
;
·
![]() ,
тогда и только тогда, когда имеется строгая нелинейная функциональная
зависимость
,
тогда и только тогда, когда имеется строгая нелинейная функциональная
зависимость ![]() от
от
![]() ;
;
·
![]() ,
тогда и только тогда, когда регрессия
,
тогда и только тогда, когда регрессия ![]() по
по ![]() строго линейная, но нет
функциональной зависимости;
строго линейная, но нет
функциональной зависимости;
·
![]() ,
указывает на то, что не существует функциональной зависимости, и некоторая
нелинейная кривая регрессии <<подходит>> лучше, чем <<наилучшая>>
прямая линия.
,
указывает на то, что не существует функциональной зависимости, и некоторая
нелинейная кривая регрессии <<подходит>> лучше, чем <<наилучшая>>
прямая линия.
Таким образом, равенство квадрата коэффициента корреляции корреляционному отношению указывает на то, что для регрессии нельзя найти лучшей кривой, чем прямая линия.
Оценка корреляционного отношения определяется выражением
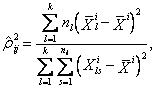 (5.2)
(5.2)
где ![]() —
количество интервалов сечений для компоненты
—
количество интервалов сечений для компоненты ![]() ;
; ![]() — среднее значение компоненты
— среднее значение компоненты ![]() в
в ![]() – м сечении;
– м сечении;
![]() —
число наблюдений компоненты
—
число наблюдений компоненты ![]() в
в ![]() – м сечении;
– м сечении; ![]() — значение
компоненты
— значение
компоненты ![]() с
номером
с
номером ![]() в
в ![]() – м
сечении.
– м
сечении.
Относительно корреляционного отношения могут проверяться два вида
гипотез: о равенстве корреляционного отношения нулю ![]() и о равенстве
корреляционного отношения квадрату коэффициента корреляции
и о равенстве
корреляционного отношения квадрату коэффициента корреляции ![]() (критерий линейности
регрессии
(критерий линейности
регрессии ![]() по
по
![]() ).
).
В критерии проверки гипотезы ![]() используется статистика
используется статистика
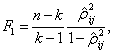 (5.3)
(5.3)
которая при справедливой гипотезе ![]() имеет
имеет ![]() – распределение Фишера с числом
степеней свободы
– распределение Фишера с числом
степеней свободы ![]() и
и ![]() :
: ![]() [58].
[58].
При проверке гипотезы ![]() вычисляется статистика
вычисляется статистика
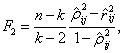 (5.4)
(5.4)
которая при справедливой гипотезе ![]() имеет
имеет ![]() – распределение Фишера с числом
степеней свободы
– распределение Фишера с числом
степеней свободы ![]() и
и ![]() :
: ![]() [58].
[58].
5.2. Влияние различных способов группирования и количества интервалов на оценку корреляционного отношения
Как ранее отмечалось, в данной работе использовались три способа
группирования: равноинтервальное (РИГ), равночастотное (РЧГ) и асимптотически
оптимальное (АОГ). Отметим, что в случае равночастотного группирования, если
количество случайных величин ![]() не делится на число интервалов
не делится на число интервалов ![]() нацело, то
остаток распределяется равномерно от центральных до крайних интервалов
группирования. Например, для
нацело, то
остаток распределяется равномерно от центральных до крайних интервалов
группирования. Например, для ![]() и
и ![]() при РЧГ будем иметь следующие
частоты попаданий в интервалы группирования
при РЧГ будем иметь следующие
частоты попаданий в интервалы группирования ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
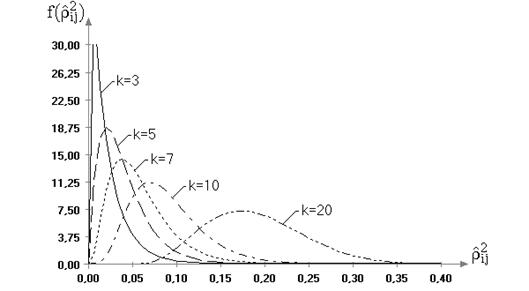
Рис. 5.1. Функции плотности распределения оценок
корреляционного отношения, моделируемых при ![]() , в случае использования РЧГ
для различного количества интервалов группирования
, в случае использования РЧГ
для различного количества интервалов группирования ![]() ,
, ![]()
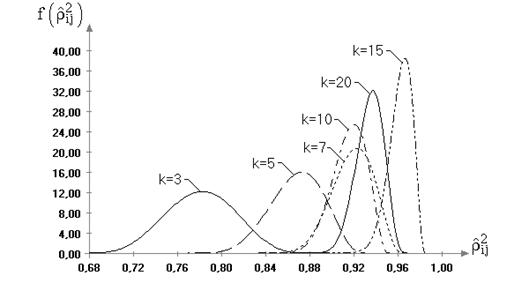
Рис. 5.2. Функции плотности распределения оценок
корреляционного отношения, моделируемых при ![]() , в случае использования РЧГ
для различного количества интервалов группирования
, в случае использования РЧГ
для различного количества интервалов группирования ![]() ,
, ![]()
Из выражения для оценки корреляционного отношения (5.2) можно
увидеть, что увеличение числа интервалов группирования ![]() приводит к росту самой
оценки. Это подтверждают рисунки 5.1 и 5.2, где изображены
полученные в результате моделирования плотности оценок корреляционного
отношения, промоделированные при
приводит к росту самой
оценки. Это подтверждают рисунки 5.1 и 5.2, где изображены
полученные в результате моделирования плотности оценок корреляционного
отношения, промоделированные при ![]() и
и ![]() соответственно и вычисленные с
использованием РЧГ при различном количестве интервалов группирования
соответственно и вычисленные с
использованием РЧГ при различном количестве интервалов группирования ![]() и объеме случайных
наблюдений
и объеме случайных
наблюдений ![]() .
На данных рисунках видно, что в общем случае с увеличением числа интервалов
.
На данных рисунках видно, что в общем случае с увеличением числа интервалов ![]() растет параметр
сдвига у функции плотности оценки. Аналогичная зависимость функций плотности
распределения оценок корреляционного отношения от количества интервалов
группирования наблюдается и в случае равноинтервального и асимптотически
оптимального способов группирования.
растет параметр
сдвига у функции плотности оценки. Аналогичная зависимость функций плотности
распределения оценок корреляционного отношения от количества интервалов
группирования наблюдается и в случае равноинтервального и асимптотически
оптимального способов группирования.
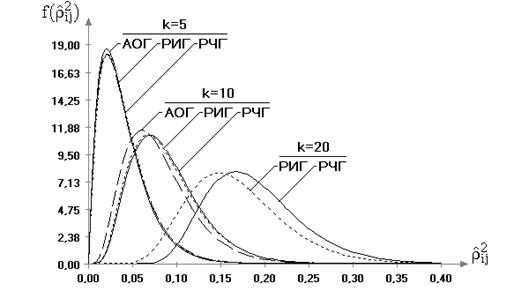
Рис. 5.3. Функции плотности распределения оценок
корреляционного отношения, моделируемых при ![]() , где использовалось АОГ,
РИГ, РЧГ для различного числа интервалов группирования
, где использовалось АОГ,
РИГ, РЧГ для различного числа интервалов группирования ![]() ,
, ![]()
Влияние способа группирования на оценку корреляционного отношения
отражено на рисунке 5.3, где моделирование проводилось при ![]() и объеме
псевдослучайных величин
и объеме
псевдослучайных величин ![]() . Для числа интервалов
. Для числа интервалов ![]() функции
плотности оценок
функции
плотности оценок ![]() , вычисленных при различных способах
группирования, совпадают. А с увеличением числа интервалов наблюдается
расхождение функций плотности оценок для разных способов группирования.
Например, при объеме
, вычисленных при различных способах
группирования, совпадают. А с увеличением числа интервалов наблюдается
расхождение функций плотности оценок для разных способов группирования.
Например, при объеме ![]() , начиная с
, начиная с ![]() плотность распределения
оценки (5.2), вычисленная при асимптотически оптимальном группировании,
смещается влево относительно функций плотности, вычисленных с использованием
РИГ или РЧГ. Различие в распределениях оценок при РЧГ и РИГ наблюдается при
плотность распределения
оценки (5.2), вычисленная при асимптотически оптимальном группировании,
смещается влево относительно функций плотности, вычисленных с использованием
РИГ или РЧГ. Различие в распределениях оценок при РЧГ и РИГ наблюдается при ![]() , когда
, когда ![]() .
.
Так как моделирование оценок корреляционного отношения
осуществлялось при ![]() , то казалось бы предпочтительней
выбрать тот способ группирования, плотность оценок которого лежит левее. С другой
стороны, рост числа интервалов группирования для АОГ и РИГ приводит к тому, что
будут появляться интервалы, для которых число наблюдений
, то казалось бы предпочтительней
выбрать тот способ группирования, плотность оценок которого лежит левее. С другой
стороны, рост числа интервалов группирования для АОГ и РИГ приводит к тому, что
будут появляться интервалы, для которых число наблюдений ![]() будет равно нулю. Для АОГ
это крайние интервалы, а для РИГ — интервалы, находящиеся между
<<удаленными>> наблюдениями и основной группой. Наличие интервалов
с нулевыми частотами попадания приводит к искусственному занижению величины
оценки корреляционного отношения
будет равно нулю. Для АОГ
это крайние интервалы, а для РИГ — интервалы, находящиеся между
<<удаленными>> наблюдениями и основной группой. Наличие интервалов
с нулевыми частотами попадания приводит к искусственному занижению величины
оценки корреляционного отношения ![]() . Использование равночастотного группирования
позволяет избежать таких ошибок.
. Использование равночастотного группирования
позволяет избежать таких ошибок.
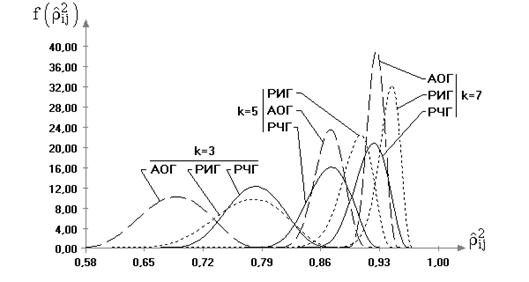
Рис. 5.4. Функции плотности распределения оценок
корреляционного отношения, моделируемых при ![]() , где использовалось АОГ,
РИГ, РЧГ для различного числа интервалов группирования
, где использовалось АОГ,
РИГ, РЧГ для различного числа интервалов группирования ![]() ,
, ![]()
Несколько сложнее выглядит ситуация когда рассматриваются оценки ![]() , моделируемые
для случая
, моделируемые
для случая ![]() .
На рисунке 5.4 изображены плотности оценок корреляционного отношения при
различных способах группирования, моделируемых при
.
На рисунке 5.4 изображены плотности оценок корреляционного отношения при
различных способах группирования, моделируемых при ![]() и объеме случайных
величин
и объеме случайных
величин ![]() .
При малом числе интервалов группирования
.
При малом числе интервалов группирования ![]() относительно объема выборки
относительно объема выборки ![]() на данном
рисунке РИГ выглядит предпочтительней, так как плотность оценок
на данном
рисунке РИГ выглядит предпочтительней, так как плотность оценок ![]() , построенная с
использованием РИГ, при равном числе интервалов расположена правее, чем
плотности оценок для АОГ и РЧГ. Но, во – первых, оценки корреляционного отношения
, построенная с
использованием РИГ, при равном числе интервалов расположена правее, чем
плотности оценок для АОГ и РЧГ. Но, во – первых, оценки корреляционного отношения
![]() ,
построенные с использованием РИГ, сильно зависят от крайних граничных точек
интервалов группирования
,
построенные с использованием РИГ, сильно зависят от крайних граничных точек
интервалов группирования ![]() и
и ![]() , так как эти точки определяют длину
интервалов. А во – вторых, как и в случае
, так как эти точки определяют длину
интервалов. А во – вторых, как и в случае ![]() , неоправданное завышение числа интервалов
при равноинтервальном группировании приводит к ухудшению свойств оценок
корреляционного отношения. Существенное изменение функций плотности оценок
, неоправданное завышение числа интервалов
при равноинтервальном группировании приводит к ухудшению свойств оценок
корреляционного отношения. Существенное изменение функций плотности оценок ![]() показано на
рисунке 5.5. Причина ухудшения свойств оценок
показано на
рисунке 5.5. Причина ухудшения свойств оценок ![]() есть описанное ранее обнуление
частот попаданий
есть описанное ранее обнуление
частот попаданий ![]() для нескольких интервалов
группирования, которое вновь приводит к искусственному занижению величины
оценки корреляционного отношения. Асимптотически оптимальное группирование при
неправильном выборе количества интервалов, что и в случае РИГ, также приводит к
искаженным функциям распределения.
для нескольких интервалов
группирования, которое вновь приводит к искусственному занижению величины
оценки корреляционного отношения. Асимптотически оптимальное группирование при
неправильном выборе количества интервалов, что и в случае РИГ, также приводит к
искаженным функциям распределения.
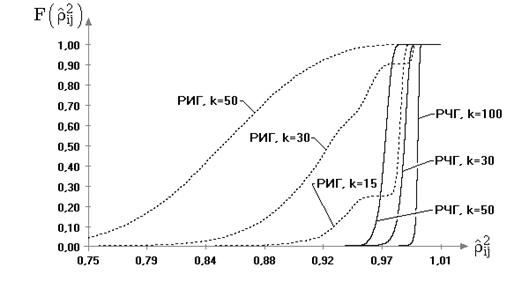
Рис. 5.5. Распределения оценок корреляционного отношения,
моделируемых при ![]() , где
использовалось РИГ, РЧГ для различного числа интервалов группирования
, где
использовалось РИГ, РЧГ для различного числа интервалов группирования ![]() ,
, ![]()
Поэтому для асимптотически оптимального и равноинтервального
группирования можно определить <<критические>> значения числа
интервалов, начиная с которых появляются нулевые частоты попадания ![]() , и, как
следствие, происходит ухудшение свойств оценок корреляционного отношения.
, и, как
следствие, происходит ухудшение свойств оценок корреляционного отношения.
Увеличение объемов выборок случайных величин не изменяет выявленной закономерности по влиянию способов и количества интервалов группирования на распределения оценок корреляционного отношения. С ростом объемов происходит естественное увеличение значений для <<критических>> чисел интервалов группирования, начиная с которых наблюдается оговоренное ухудшение свойств оценок корреляционного отношения при использовании АОГ или РИГ.
Для вычислений оценок корреляционного отношения можно рекомендовать
использовать равночастотное группирование, так как в данном случае свойства
вычисляемых оценок меньше зависят от числа интервалов группирования. Если по
каким – либо причинам было принято решение о применении АОГ или РИГ, тогда
прежде всего требуется убедиться, что при разбиении на интервалы отсутствуют
нулевые частоты попаданий ![]() , в противном случае надо уменьшить
число интервалов.
, в противном случае надо уменьшить
число интервалов.
5.3. Исследование распределений статистики критерия проверки гипотезы о незначимости корреляционного отношения
В первую очередь с помощью методов статистического моделирования исследовались распределения статистик, используемых при проверке гипотез о корреляционном отношении, при условии, что наблюдения принадлежат многомерному нормальному закону.
Исследование распределения статистики критерия проверки гипотез о
равенстве корреляционного отношения нулевому значению показало, что если
осуществляется корректный выбор количества интервалов группирования ![]() , то
соответствующее теоретическое предельное
, то
соответствующее теоретическое предельное ![]() – распределение с
– распределение с ![]() и
и ![]() числом степеней
свободы хорошо описывает эмпирическое распределение статистики
числом степеней
свободы хорошо описывает эмпирическое распределение статистики ![]() .
.
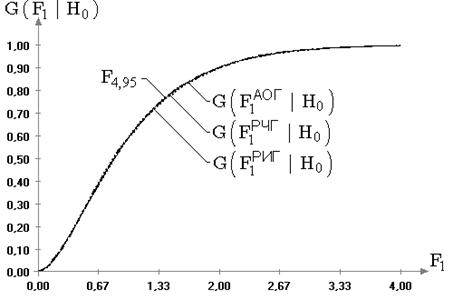
Рис. 5.6. Теоретическая и эмпирические функции распределения
статистики ![]() (5.3)
при проверке гипотезы
(5.3)
при проверке гипотезы ![]() ,
построенные с использованием различных способов группирования:
,
построенные с использованием различных способов группирования: ![]() ,
, ![]()
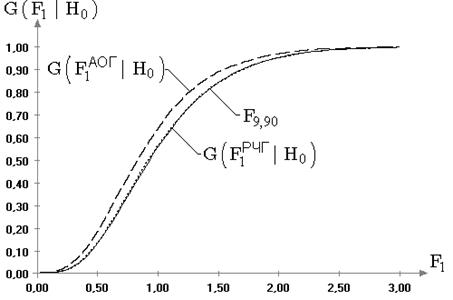
Рис. 5.7. Теоретическая и эмпирические функции распределения
статистики ![]() (5.3)
при проверке гипотезы
(5.3)
при проверке гипотезы ![]() ,
построенные с использованием АОГ и РЧГ:
,
построенные с использованием АОГ и РЧГ: ![]() ,
, ![]()
Например, на рисунке 5.6 представлены полученные в результате
моделирования эмпирические распределения статистики ![]() (5.3), построенные с
использованием АОГ, РЧГ и РИГ, а также соответствующее предельное
(5.3), построенные с
использованием АОГ, РЧГ и РИГ, а также соответствующее предельное ![]() — распределение
при проверке гипотезы
— распределение
при проверке гипотезы ![]() для числа интервалов
для числа интервалов ![]() и объема выборки
и объема выборки
![]() .
Рисунок дополнен таблицей, где отражены результаты проверки согласия эмпирического
распределения с теоретическим предельным по критериям согласия. Приведенные
уровни значимости по критериям согласия свидетельствуют о том, что статистика
.
Рисунок дополнен таблицей, где отражены результаты проверки согласия эмпирического
распределения с теоретическим предельным по критериям согласия. Приведенные
уровни значимости по критериям согласия свидетельствуют о том, что статистика ![]() действительно
хорошо описывается соответствующим предельным распределением, и на данное согласие
существенно не влияет выбор способа группирования при правильном выборе
действительно
хорошо описывается соответствующим предельным распределением, и на данное согласие
существенно не влияет выбор способа группирования при правильном выборе ![]() .
.
Пример некорректного выбора числа интервалов для асимптотически
оптимального группирования приведен на рисунке 5.7. Где явно видно
изменение предельного закона распределения статистики ![]() при АОГ, в то время когда
использование равночастотного группирования дает по – прежнему высокие
значения для достигаемых уровней значимости. Превышение
<<критических>> значений для числа интервалов
при АОГ, в то время когда
использование равночастотного группирования дает по – прежнему высокие
значения для достигаемых уровней значимости. Превышение
<<критических>> значений для числа интервалов ![]() приводит к изменению
предельного распределения статистики
приводит к изменению
предельного распределения статистики ![]() и в случае применения равноинтервального
группирования.
и в случае применения равноинтервального
группирования.
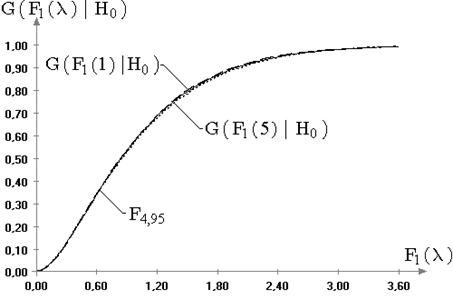
Рис. 5.8. Эмпирические функции распределения статистик ![]() ,
, ![]() и классическое предельное
и классическое предельное ![]() – распределение при
проверке гипотезы
– распределение при
проверке гипотезы ![]() : РЧГ,
: РЧГ, ![]() ,
, ![]()
Исследование распределений статистики, используемой при проверке
гипотезы вида ![]() ,
проводилось для законов многомерных величин, моделируемых на основе
предложенной в данной работе процедуры при различных способах группирования.
,
проводилось для законов многомерных величин, моделируемых на основе
предложенной в данной работе процедуры при различных способах группирования.
Из результатов, приведенных на рисунке 5.8, следует, что нет
оснований для отклонения предположения о том, что предельным распределением
статистики критерия проверки гипотезы о равенстве корреляционного отношения
нулевому значению в случае многомерных законов, построенных по семейству
распределений (6.4) с разными параметрами формы ![]() , является классическое
предельное
, является классическое
предельное ![]() – распределение
Фишера с числом степеней свободы
– распределение
Фишера с числом степеней свободы ![]() и
и ![]() .
.
Таблица 5.1. Значения достигнутых уровней значимости по
критериям согласия для распределений статистики ![]() , смоделированных при
различных параметрах формы
, смоделированных при
различных параметрах формы ![]() :
: ![]() и
и ![]()
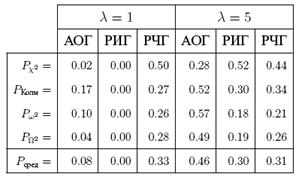
Исследование влияния способа группирования на распределение статистики
![]() при
многомерных законах, отличных от нормального, показало еще большую зависимость
оценок корреляционного отношения от числа интервалов
при
многомерных законах, отличных от нормального, показало еще большую зависимость
оценок корреляционного отношения от числа интервалов ![]() при использовании асимптотически
оптимального и равноинтервального группирования. В таблице 5.1 приведены
значения достигаемых уровней значимости при проверке согласия между
эмпирическим распределением статистики
при использовании асимптотически
оптимального и равноинтервального группирования. В таблице 5.1 приведены
значения достигаемых уровней значимости при проверке согласия между
эмпирическим распределением статистики ![]() и соответствующим классическим
предельным
и соответствующим классическим
предельным ![]() – распределением.
Эксперименты показали, что в случае более островершинных многомерных законах
для методов АОГ и РИГ желательно еще большее уменьшение числа интервалов
группирования по сравнению с нормальным законом, а для более плосковершинных
законов — наоборот, допустимо увеличение количества интервалов.
– распределением.
Эксперименты показали, что в случае более островершинных многомерных законах
для методов АОГ и РИГ желательно еще большее уменьшение числа интервалов
группирования по сравнению с нормальным законом, а для более плосковершинных
законов — наоборот, допустимо увеличение количества интервалов.
Для многомерных законов, моделируемых по семейству
распределений (6.4), использование равночастотного группирования не
ухудшает согласия между эмпирическим распределением статистики ![]() и соответствующим
классическим предельным при любом выборе числа интервалов как при
и соответствующим
классическим предельным при любом выборе числа интервалов как при ![]() , так и
, так и ![]() . По–прежнему,
разбиение допустимой области на интервалы с равными частотами попадания
. По–прежнему,
разбиение допустимой области на интервалы с равными частотами попадания ![]() видится более
предпочтительным.
видится более
предпочтительным.
Таким образом, результаты исследования распределений статистики ![]() показали, что в
случае многомерных законов, достаточно существенно отличающихся от нормального
(более островершинных или более плосковершинных, и даже в случае многомерного
закона, построенного по несимметричному одномерному распределению), значимого изменения
предельного распределения статистики
показали, что в
случае многомерных законов, достаточно существенно отличающихся от нормального
(более островершинных или более плосковершинных, и даже в случае многомерного
закона, построенного по несимметричному одномерному распределению), значимого изменения
предельного распределения статистики ![]() не происходит.
не происходит.
Это позволяет утверждать, что статистические выводы, опирающиеся на классический
аппарат, в задачах с применением критерия проверки гипотезы вида ![]() будут оставаться
корректными и при нарушении предположений о нормальности наблюдаемого
многомерного закона.
будут оставаться
корректными и при нарушении предположений о нормальности наблюдаемого
многомерного закона.
5.4. Исследование распределений статистики критерия
линейности регрессии 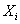 по
по 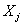
Указанные в начале данной главы соотношения ![]() между теоретическими корреляционным
отношением
между теоретическими корреляционным
отношением ![]() и
парным коэффициентом корреляции
и
парным коэффициентом корреляции ![]() не всегда выполняются для их
оценок, особенно, если связь (регрессионная или функциональная) линейная. Такое
возможно, если
не всегда выполняются для их
оценок, особенно, если связь (регрессионная или функциональная) линейная. Такое
возможно, если ![]() и
и
![]() близки[103].
Нарушение условия происходит из–за вычислительных погрешностей, связанных с
ограниченностью представления чисел в ЭВМ, случайностью оценок
близки[103].
Нарушение условия происходит из–за вычислительных погрешностей, связанных с
ограниченностью представления чисел в ЭВМ, случайностью оценок ![]() и
и ![]() и сильным
влиянием на
и сильным
влиянием на ![]() числа
интервалов и способов группирования. Известно, что величина
числа
интервалов и способов группирования. Известно, что величина ![]() является индикатором
нелинейности [58]. Однако, как уже говорилось, величина
является индикатором
нелинейности [58]. Однако, как уже говорилось, величина ![]() вследствие случайности
оценок может оказаться отрицательной, хотя абсолютная величина разности, как
правило, мала.
вследствие случайности
оценок может оказаться отрицательной, хотя абсолютная величина разности, как
правило, мала.
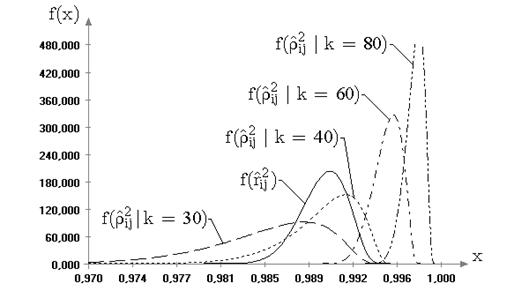
Рис. 5.9. Функции плотности распределения оценок
корреляционного отношения ![]() и
квадрата парного коэффициента корреляции
и
квадрата парного коэффициента корреляции ![]() , моделируемых при линейной
зависимости
, моделируемых при линейной
зависимости ![]() от
от ![]() : РЧГ,
: РЧГ, ![]()
Возможность нарушения неравенства ![]() для соответствующих оценок наглядно
иллюстрирует рисунок 5.9, где представлены функции плотности квадрата
оценки парного коэффициента корреляции
для соответствующих оценок наглядно
иллюстрирует рисунок 5.9, где представлены функции плотности квадрата
оценки парного коэффициента корреляции ![]() и плотности оценок корреляционного
отношения
и плотности оценок корреляционного
отношения ![]() ,
построенные для случая линейной зависимости
,
построенные для случая линейной зависимости ![]() от
от ![]() (
(![]() ). При вычислении оценок
корреляционного отношения использовались интервалы равной частоты при объемах
выборок случайных величин
). При вычислении оценок
корреляционного отношения использовались интервалы равной частоты при объемах
выборок случайных величин ![]() . На приведенном рисунке видно, что
для объема
. На приведенном рисунке видно, что
для объема ![]() с
ростом числа интервалов группирования вероятность появления значений
с
ростом числа интервалов группирования вероятность появления значений ![]() падает
(плотности оценок <<расходятся>> дальше друг от друга), но остается
положительной.
падает
(плотности оценок <<расходятся>> дальше друг от друга), но остается
положительной.
При увеличении объемов выборок ![]() уменьшается дисперсия распределения
оценки парного коэффициента корреляции. Поэтому для больших значений
уменьшается дисперсия распределения
оценки парного коэффициента корреляции. Поэтому для больших значений ![]() и
и ![]() вероятность
появления значений
вероятность
появления значений ![]() оказывается практически близкой к
нулю. На рисунке 5.10 отображены плотности оценок
оказывается практически близкой к
нулю. На рисунке 5.10 отображены плотности оценок ![]() и
и ![]() , вид которых позволяет
утверждать, что при объеме выборки
, вид которых позволяет
утверждать, что при объеме выборки ![]() и числе интервалов группирования
и числе интервалов группирования ![]() при использовании
РЧГ неравенство
при использовании
РЧГ неравенство ![]() с вероятностью 1 выполняется и для
их оценок.
с вероятностью 1 выполняется и для
их оценок.
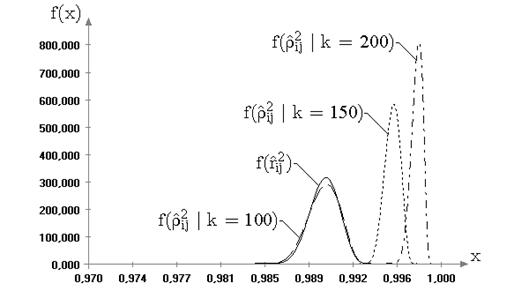
Рис. 5.10. Функции плотности распределения оценок
корреляционного отношения ![]() и
квадрата парного коэффициента корреляции
и
квадрата парного коэффициента корреляции ![]() , моделируемых при линейной
зависимости
, моделируемых при линейной
зависимости ![]() от
от ![]() : РЧГ,
: РЧГ, ![]()
Однако и при значениях ![]() и
и ![]() распределение статистики
распределение статистики ![]() даже в случае
многомерного нормального закона не подчиняется
даже в случае
многомерного нормального закона не подчиняется ![]() – распределению Фишера с числом
степеней свободы
– распределению Фишера с числом
степеней свободы ![]() и
и ![]() (см. рис. 5.11). Дальнейшее
увеличение объемов выборок и числа интервалов группирования существенно не
улучшает согласия между распределением данной статистики и соответствующим
предельным распределением.
(см. рис. 5.11). Дальнейшее
увеличение объемов выборок и числа интервалов группирования существенно не
улучшает согласия между распределением данной статистики и соответствующим
предельным распределением.
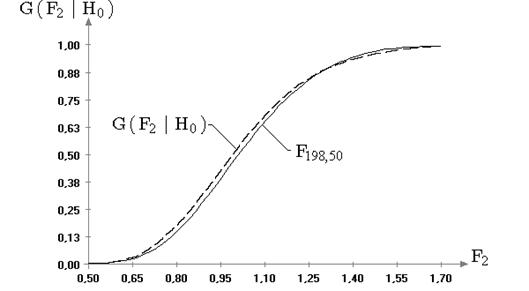
Рис. 5.11. Теоретическая и эмпирическая функции распределения
статистики ![]() (5.4)
при проверке гипотезы
(5.4)
при проверке гипотезы ![]() : РЧГ,
: РЧГ, ![]() ,
, ![]()
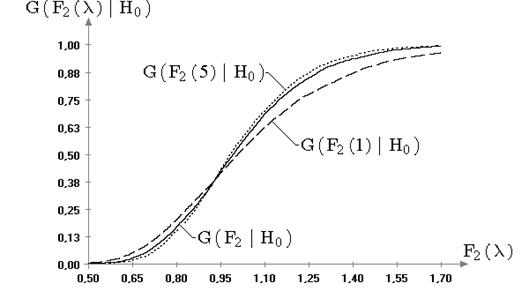
Рис. 5.12. Эмпирические функции распределения статистик ![]() ,
, ![]() и
и ![]() при проверке гипотезы
при проверке гипотезы ![]() : РЧГ,
: РЧГ, ![]() ,
, ![]()
С другой стороны, проведенные исследования не опровергают, что
распределение статистики ![]() подчиняется
подчиняется ![]() – распределению в
пределе
– распределению в
пределе ![]() .
При обработке реальных данных, когда вычисленное значение статистики
оказывается
.
При обработке реальных данных, когда вычисленное значение статистики
оказывается ![]() ,
можно рекомендовать рассмотреть значения оценок
,
можно рекомендовать рассмотреть значения оценок ![]() и
и ![]() . И если они близки к единице можно
выдвинуть предположение о линейной зависимости.
. И если они близки к единице можно
выдвинуть предположение о линейной зависимости.
В случае многомерного закона, отличного от нормального, есть
основания утверждать, что ни для конечных объемов выборок, ни при ![]() распределение
статистики
распределение
статистики ![]() не
будет описываться
не
будет описываться ![]() – распределением. Это следует,
во–первых, из различия эмпирических распределений статистики
– распределением. Это следует,
во–первых, из различия эмпирических распределений статистики ![]() для многомерного
нормального закона и законов, моделируемых на основе семейства
распределений (6.4) с параметрами формы
для многомерного
нормального закона и законов, моделируемых на основе семейства
распределений (6.4) с параметрами формы ![]() и
и ![]() (см. рис. 5.12). Во-вторых, из
показанной ранее неустойчивости критерия проверки гипотез о парном коэффициенте
корреляции вида
(см. рис. 5.12). Во-вторых, из
показанной ранее неустойчивости критерия проверки гипотез о парном коэффициенте
корреляции вида ![]() , при
, при ![]() к отклонению от нормальности.
к отклонению от нормальности.
5.5. Выводы
Исследование влияния способов группирования и количества интервалов
на оценку корреляционного отношения показало, что оценка корреляционного
отношения, прежде всего, сильно зависит от количества интервалов группирования.
Как правило, уменьшение количества интервалов группирования приводит к
уменьшению значений оценок корреляционного отношения, в то время как увеличение
сопровождается ростом величины ![]() . При использовании асимптотически
оптимального и равноинтервального группирования необходимо корректно выбирать
число интервалов, избегая нулевых частот попадания
. При использовании асимптотически
оптимального и равноинтервального группирования необходимо корректно выбирать
число интервалов, избегая нулевых частот попадания ![]() в интервалы, приводящих к
ухудшению свойств оценок корреляционного отношения. Разбиение области определения
на интервалы равной частоты показало себя как наиболее предпочтительное для
вычисления оценок
в интервалы, приводящих к
ухудшению свойств оценок корреляционного отношения. Разбиение области определения
на интервалы равной частоты показало себя как наиболее предпочтительное для
вычисления оценок ![]() .
.
Исследования распределения статистики, используемой в критерии
проверки гипотезы вида ![]() , при псевдослучайных величинах,
подчиняющихся многомерному нормальному закону, показали, что оно хорошо
согласуется с теоретическим предельным распределением, полученными в классическом
корреляционном анализе. В случае многомерных законов, отличающихся от
нормального в достаточно широких пределах (более островершинных или более
плосковершинных), изменения предельного распределения статистики
, при псевдослучайных величинах,
подчиняющихся многомерному нормальному закону, показали, что оно хорошо
согласуется с теоретическим предельным распределением, полученными в классическом
корреляционном анализе. В случае многомерных законов, отличающихся от
нормального в достаточно широких пределах (более островершинных или более
плосковершинных), изменения предельного распределения статистики ![]() не происходит.
Эмпирическое распределение данной статистики по–прежнему хорошо описывается
предельными законами, полученными в предположении о нормальности наблюдаемого
вектора.
не происходит.
Эмпирическое распределение данной статистики по–прежнему хорошо описывается
предельными законами, полученными в предположении о нормальности наблюдаемого
вектора.
Полное исследование распределения статистики критерия, используемого
при проверке гипотезы вида ![]() , на данный момент затруднено
вследствие указанных вычислительных проблем, суть которых заключается в том,
что при линейной связи соотношение для теоретических величин
, на данный момент затруднено
вследствие указанных вычислительных проблем, суть которых заключается в том,
что при линейной связи соотношение для теоретических величин ![]() может не
выполняться для их оценок.
может не
выполняться для их оценок.
Глава 6. Описание программной системы
6.1. Общая характеристика программной системы
Методика компьютерного моделирования и анализа статистических закономерностей предполагает разработку соответствующего программного обеспечения для проведения исследований. Программная система предназначена для осуществления проверки рассматриваемых гипотез многомерного анализа, исследования распределений статистик критериев, вычисления оценок параметров многомерных законов, моделирования выборок различных одномерных и многомерных законов распределения. Разработанное программное обеспечение является продолжением и расширением основной идеи, заложенной еще в программной системе <<Корреляционный анализ многомерных случайных величин>> [65].
Изначально программная система разрабатывалась как функциональное расширение исследовательского программного пакета <<Интервальная статистика (ISW)>>, разработанного Лемешко Б. Ю. и Постоваловым С. Н. Но в процессе реализации была оформлена как самостоятельная система. При этом использование совместимого формата данных позволило провести исследование распределений статистик, вычисляемых в критериях многомерного анализа, при помощи системы <<Интервальной статистики (ISW)>>, хорошо зарекомендовавшей себя в задачах такого рода[111,112].
Программная система позволяет решать следующие задачи:
· моделирование выборок псевдослучайных величин, подчиненных заданному закону распределения;
· моделирование выборок псевдослучайных векторов по методу, предложенному в диссертационной работе;
· моделирование распределений статистик, используемых при проверке гипотез о математическом ожидании и дисперсии;
· моделирование распределений статистик рассматриваемых критериев многомерного анализа;
· осуществлять проверку различных гипотез при помощи критериев многомерного анализа;
· строить оценки вектора математических ожиданий, ковариационной матрицы, парных, частных и множественных коэффициентов корреляции, корреляционного отношения.
Независимость ряда решаемых задач позволила спроектировать программную систему в виде совокупности самостоятельных блоков, что существенно упростило процесс разработки. Выбранный подход к реализации данных блоков позволяет легко использовать их функциональность в других программных системах. Например, блок моделирования псевдослучайных величин был реализован в виде подключаемой библиотеки.
При реализации были выделены следующие основные блоки.
· Блок моделирования одномерных и многомерных случайных величин, подчиняющихся различным законам распределения.
· Блок проверки гипотез.
· Процедуры вычисления оценок.
· Блок моделирования распределений статистик, используемых при проверке гипотез рассматриваемых критериев.
Код программный системы написан на языке C++ [105] в среде быстрой разработки приложений Borland C++ Builder 6.0 [34] с поддержкой объектно–ориентированного подхода и откомпилирован под 32–разрядные операционные системы семейства Microsoft Windows. Чтобы избежать возможных ошибок реализации математических соотношений, для нескольких алгоритмов были написаны дублирующие программы в среде математического программирования Maple [46,96].
6.2. Краткое описание интерфейса программной системы
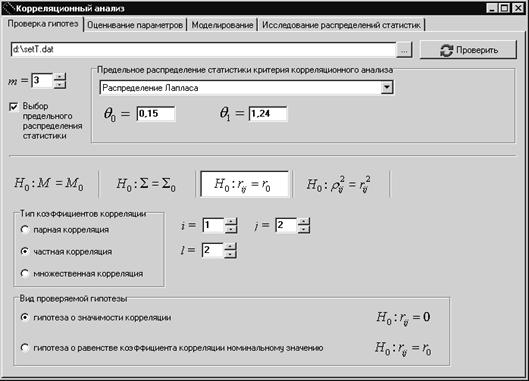
Рис. 6.1. Диалоговое окно «Проверка гипотез о коэффициентах корреляции»
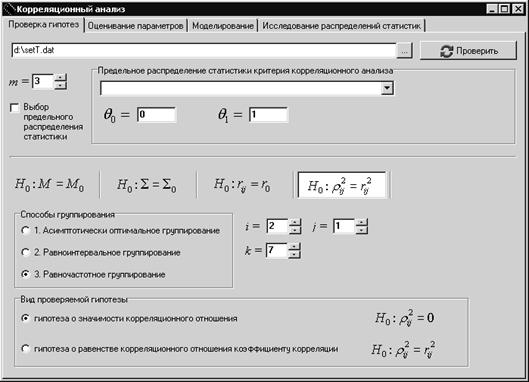
Рис. 6.2. Диалоговое окно «Проверка гипотез о корреляционном отношении»
Программная система состоит из двух программ. Основная программа, которая носит название «Корреляционный анализ», позволяет решать и исследовать задачи многомерного анализа. Вспомогательная программа позволяет моделировать распределения статистик, используемых при проверке гипотез о математическом ожидании и дисперсии в одномерном случае.
6.2.1. Основная программа
Первая закладка «Проверка гипотез» на главном диалоговом окне
позволяет выбирать вид проверяемой гипотезы: гипотезу о равенстве вектора
математических ожиданий заданному вектору ![]() ; гипотезу о равенстве
ковариационной матрицы заданной матрице
; гипотезу о равенстве
ковариационной матрицы заданной матрице ![]() ; гипотезу о значении парного,
частного и множественного коэффициентов корреляции
; гипотезу о значении парного,
частного и множественного коэффициентов корреляции ![]() ; гипотезу о
корреляционном отношении
; гипотезу о
корреляционном отношении ![]() . Общими параметрами при проверке
гипотез являются размерность, имя файла с выборкой случайных векторов и
распределение статистики критерия проверяемой гипотезы. В зависимости от
выбранного типа гипотезы может потребоваться задание дополнительных параметров.
Например, для корреляционного отношения это способ группирования, количество
интервалов группирования и сам вид проверяемой гипотезы (см. рисунки 6.1
и 6.2).
. Общими параметрами при проверке
гипотез являются размерность, имя файла с выборкой случайных векторов и
распределение статистики критерия проверяемой гипотезы. В зависимости от
выбранного типа гипотезы может потребоваться задание дополнительных параметров.
Например, для корреляционного отношения это способ группирования, количество
интервалов группирования и сам вид проверяемой гипотезы (см. рисунки 6.1
и 6.2).
Выбор и вычисление оценок рассматриваемых параметров по выборке случайных векторов можно осуществить через закладку «Оценивание параметров». Полученные результаты оформляются в виде HTML отчета средствами специально разработанной библиотеки. Изменение или доработка программного кода данной библиотеки позволяет легко добиться улучшения вида получаемого отчета без вмешательства в код основной программы.
Доступ к процедурам моделирования, описанным в разделе 6.3, осуществляется через одноименную закладку основного диалогового окна (рис. 6.3).
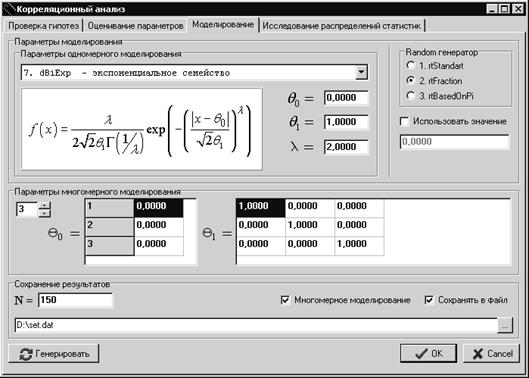
Рис. 6.3. Диалоговое окно «Моделирование»
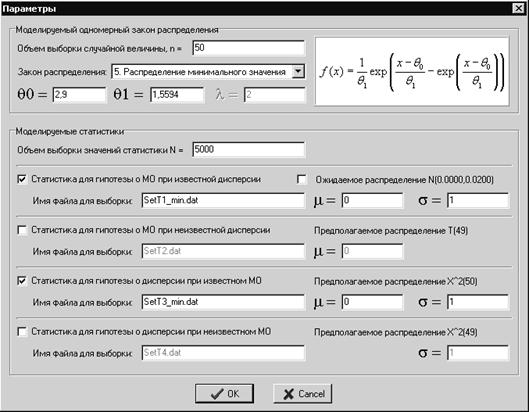
Рис. 6.4. Программа для исследования распределений статистик в одномерном случае
Закладка «Исследование распределений статистик» не содержит множества задаваемых параметров, кроме имени файла для выгрузки выборки значений статистики. При моделировании выборки используются установленные параметры на предыдущих закладках. В этом случае закладка «Моделирование» определяет закон распределения генерируемого псевдослучайного вектора, а «Проверка гипотез» — статистику критерия, используемую при проверке выбранной гипотезы.
6.2.2. Вспомогательная программа
Для исследования одномерного случая, когда проверяются гипотезы о математическом ожидании и дисперсии, написана вспомогательная программа. Она позволяется моделировать распределения статистик, используемых при проверке данных гипотез (см. рисунок 6.4).
6.3. Моделирование псевдослучайных величин
Для проведения исследований по теме диссертационной работы ключевым блоком программной системы является блок моделирования. Средствами программной системы можно производить моделирование одномерных и многомерных псевдослучайных величин.
При построении любой системы статистического моделирования центральным элементом является датчик, генерирующий псевдослучайные числа по равномерному закону. Проверка качества такого датчика является непременным условием его использования. Важно, не только то, чтобы получаемые последовательности при любых объемах выборок хорошо соответствовали равномерному закону, но и то, чтобы они удовлетворяли целям исследований[50,92]. Всегда хорошей дополнительной проверкой качества датчиков может являться построение в результате моделирования той статистической закономерности, которая является известным достоянием теории. Хорошее совпадение результатов моделирования с теоретическими является косвенным подтверждением качества используемого датчика.
В программную систему включены следующие алгоритмы имитации псевдослучайной величины, равномерно распределенной на отрезке (0, 1): встроенный датчик систем программирования C++ и мультипликативный датчик [6, 15, 51, 52, 110]. Оба датчика удовлетворяют требованиям, позволяющим использовать их в целях исследования статистических закономерностей.
Исследование датчиков проведено в работе [92], где было отмечено, что выбранные подходы к имитации псевдослучайной величины позволяют получать последовательности, достаточно хорошо подчиняющиеся равномерному закону при различных объемах выборок. Они удовлетворяют требованиям, позволяющим использовать их в целях исследования статистических закономерностей. Датчик в системах программирования С++ обладает приемлемыми свойствами равномерности, но имеет один недостаток, который следует иметь в виду: в генерируемых выборках, начиная с объемов, примерно, в 1700–1800 наблюдений, начинают появляться повторные значения (этот недостаток исчезает при использовании вычислений с двойной точностью). Реализация мультипликативного датчика такого недостатка не имеет[52]. Поэтому в диссертационной работе при проведении исследований использовался мультипликативный алгоритм, так как для моделирования выборок значений статистик критериев требовались достаточно большие объемы выборок псевдослучайных величин, равномерно распределенных на отрезке (0, 1) .
В программной системе для реализации алгоритмов моделирования использовался объектно–ориентированный подход. Преимуществом такого построения программного кода является то, что при необходимости программная система может быть легко расширена любыми законами распределения. И тогда можно исследовать распределения статистик соответствующих критериев для добавленных одномерных и многомерных законов.
6.3.1. Моделирование одномерных распределений
Основные алгоритмы для имитации одномерных выборочных значений были
взяты из [40,51,52,66], где наиболее часто используемым и общим методом
формирования псевдослучайных величин является метод обратных функций. В этом
методе случайная величина ![]() , подчиняющаяся закону с функцией
распределения
, подчиняющаяся закону с функцией
распределения ![]() ,
получается в соответствии с соотношением
,
получается в соответствии с соотношением ![]() , где
, где ![]() – функция, обратная к
– функция, обратная к ![]() , а
, а ![]() – случайная
величина, равномерно распределенная на интервале (0, 1).
– случайная
величина, равномерно распределенная на интервале (0, 1).
Введем обозначения аналогично [66]:
![]() – случайные
величины, равномерно распределенные на интервале (0, 1);
– случайные
величины, равномерно распределенные на интервале (0, 1);
![]() – случайные
величины, распределенные по стандартному нормальному закону с параметрами
(0, 1);
– случайные
величины, распределенные по стандартному нормальному закону с параметрами
(0, 1);
![]() — параметр сдвига;
— параметр сдвига;
![]() — параметр масштаба;
— параметр масштаба;
![]() —
математическое ожидание случайной величины
—
математическое ожидание случайной величины ![]() ;
;
![]() — дисперсия случайной величины
— дисперсия случайной величины ![]() .
.
Тогда согласно [40,41,52]:
Пара псевдослучайных чисел, распределенных по стандартному нормальному закону с параметрами (0, 1), генерируется по формулам
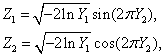 (6.1)
(6.1)
а нормальное распределение с математическим ожиданием ![]() и дисперсией
и дисперсией ![]()
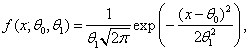 (6.2)
(6.2)
получается преобразованием стандартной величины
![]() (6.3)
(6.3)
Псевдослучайная величина, принадлежащая семейству распределений с функцией плотности
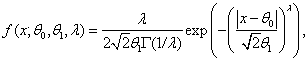 (6.4)
(6.4)
![]()
где ![]() —
параметр формы, находится из численного решения уравнения
—
параметр формы, находится из численного решения уравнения ![]() , так как в этом случае
обратная функция
, так как в этом случае
обратная функция ![]() не выражается явно.
не выражается явно.
Дополнительно в программной системе реализовано моделирование псевдослучайных величин, подчиняющихся законам распределения, приведенным в таблице 6.1.
6.3.2. Моделирование псевдослучайных нормальных векторов
Многомерное нормальное распределение случайного вектора ![]() размерности
размерности ![]() полностью определяется
вектором математических ожиданий
полностью определяется
вектором математических ожиданий ![]() и ковариационной матрицей
и ковариационной матрицей ![]() .
.
Функция плотности многомерного нормального закона имеет вид
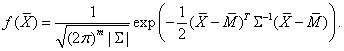 (6.5)
(6.5)
Хорошо зарекомендовавший себя алгоритм генерирования псевдослучайных
нормальных векторов был подробно изложен в [52]. Пусть мы имеем совокупность
случайных величин ![]() , где
, где ![]() подчиняется стандартному
нормальному закону с параметрами (0, 1). Тогда вектор
подчиняется стандартному
нормальному закону с параметрами (0, 1). Тогда вектор ![]() , распределенный по
многомерному нормальному закону с параметрами
, распределенный по
многомерному нормальному закону с параметрами ![]() и
и ![]() , получается через линейное
преобразование вида
, получается через линейное
преобразование вида
![]() (6.6)
(6.6)
В (6.6) обычно полагают, что ![]() является нижней треугольной
матрицей
является нижней треугольной
матрицей

тогда коэффициенты ![]() легко определяются рекуррентной
процедурой:
легко определяются рекуррентной
процедурой:
 (6.7)
(6.7)
через соотношение (6.6) и элементы ковариационной матрицы
![]()
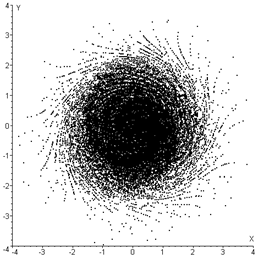
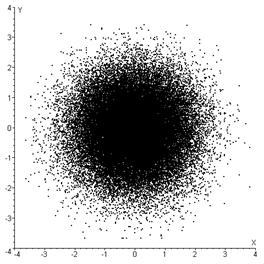
 (6.8)
(6.8)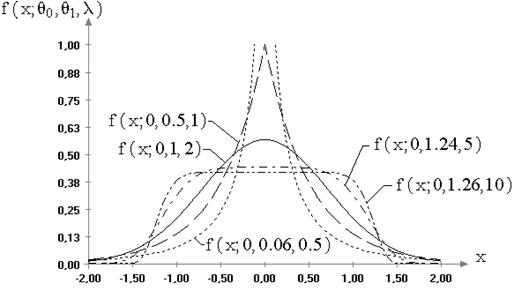
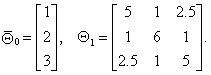
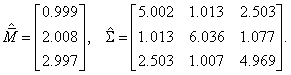
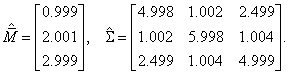
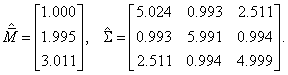
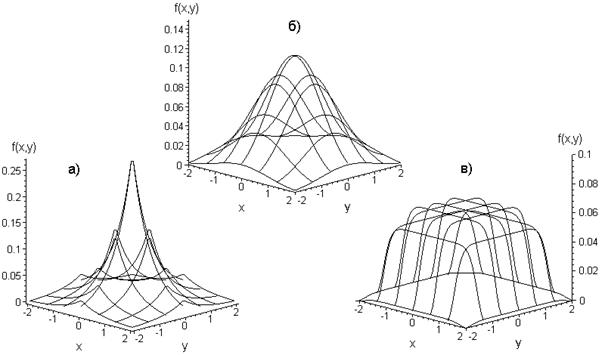
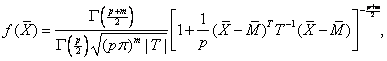 (6.19)
(6.19)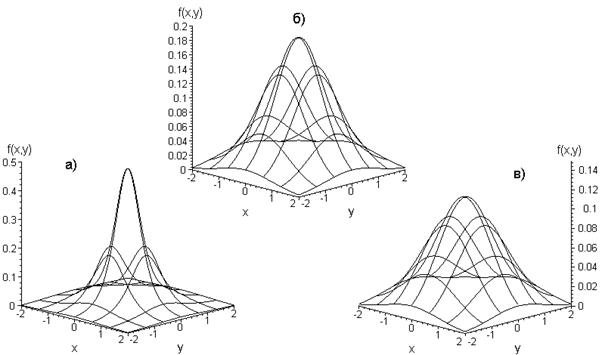
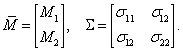
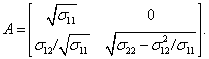 (6.21)
(6.21)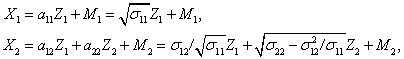 (6.22)
(6.22)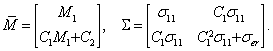 (6.24)
(6.24)