Материалы 6-й всероссийской НТК "Информационные технологии в науке, проектировании и производстве". Н.Новгород, 2002. - С.1-5.
Б.Ю. ЛЕМЕШКО (д.т.н., профессор), В.М. ПОНОМАРЕНКО (аспирант),
Е.А. ТРУШИНА (аспирант)
(Новосибирский государственный технический университет)
К ПРОВЕРКЕ СТАТИСТИЧЕСКИХ ГИПОТЕЗ В РЕГРЕССИОННОМ И ДИСПЕРСИОННОМ АНАЛИЗАХ ПРИ НАРУШЕНИИ ПРЕДПОЛОЖЕНИЙ О НОРМАЛЬНОСТИ ОШИБОК[1]
В классических регрессионном и дисперсионном анализах аппарат проверки статистических гипотез базируется на предположении нормальности закона ошибок наблюдений. Нарушение данного предположения по-разному отражается на распределениях статистик используемых критериев проверки гипотез. Предельные распределения статистик критериев могут зависеть от закона распределения ошибок и применяемого метода оценивания параметров.
В данной
работе исследуются распределения статистик, используемых при проверке гипотез в
линейном регрессионном и дисперсионном анализах, при различных отклонениях
закона распределения ошибок от нормального. В качестве возможных законов
распределений ошибок рассматриваются распределения: логистическое с
плотностью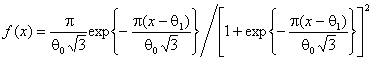 
,
Коши с плотностью 
, экспоненциальное семейство (ЭС)
распределений с плотностью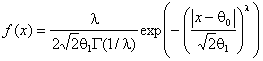 
при
различных значениях параметра формы 
.
Рассматриваемая модель отклика имеет вид
,
(1)
где 
– вектор наблюдений
размерности 
,
– матрица
независимых переменных размерности (
), отражающая структуру проводимых
экспериментов, 
–
вектор оцениваемых параметров размерности 
, 
– вектор ошибок наблюдения системы
размерности (
).
В регрессионном анализе матрица называется регрессором системы, в
дисперсионном анализе – матрицей планирования. Обозначим 
– ранг матрицы .
В самом общем виде линейную гипотезу относительно параметров можно представить следующим образом
,
(2)
где 
- известная матрица 
, 
; 
- заданный вектор 
, 
- оценка вектора параметров
,
определяемая, в нашем случае, методом максимального правдоподобия (ММП). Для
проверки гипотез в регрессионном и дисперсионном анализах используется
статистика вида:
,
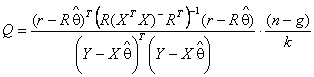(3)
где 
– матрица, обобщенно-обратная к 
, совпадающая с
матрицей 
в
случае, если 
является
матрица полного ранга, т.е. 
. В [1, 2] показано, что в случае нормальности ошибок наблюдений, статистика (3) подчиняется закону распределения Фишера 
со
степенями свободы k и n-g. Отметим, что
распределение Фишера является частным случаем бета-распределения II рода:
, (4)
где плотность бета-распределения задается выражением [3]
.
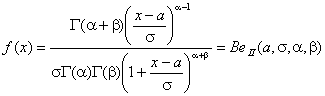Исследование распределений статистики вида (3) в случае отклонения распределения ошибок наблюдений от нормального проводилось с помощью хорошо зарекомендовавшей себя [4, 5] методики компьютерного моделирования. Методика предусматривает моделирование выборок значений исследуемых статистик и сглаживание полученных выборок наиболее подходящим теоретическим распределением. Для более точного определения модели (предельного) распределения статистики параметры аппроксимирующего закона усредняются по множеству экспериментов (по серии смоделированных выборок статистики).
Рассмотрим некоторые результаты исследований, полученные в рамках регрессионного и дисперсионного анализов.
Простейшей
гипотезой, рассматриваемой в регрессионном анализе, является гипотеза об
адекватности оценок вектора неизвестных параметров истинным значениям. В этом
случае выражение (2) записывается следующим образом
,
(5)
а статистика (3) значительно
упрощается и принимает вид (учитывая, что в регрессионном анализе ):
.
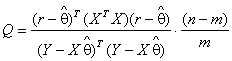(6)
В [1] показано, что в случае нормального закона
распределения отклонений регрессии (будем называть этот случай
«классическим») предельным распределением статистики (6) является распределение
Фишера со степенями свободы m и n-m, т.е. 
.
Проведенные исследования показали, что в большинстве
рассмотренных нами случаев эмпирические функции распределения статистики (6),
полученные в результате моделирования, при использовании для оценивания вектора
параметров регрессии метода максимального правдоподобия хорошо описываются бета-распределением
II рода. Для различных значений числа наблюдений n и количества m
оцениваемых параметров линейной регрессии найдены значения параметров бета-распределения
II рода, аппроксимирующего в соответствующем случае распределение статистики
(6). Найденные аппроксимации могут выступать при проверке гипотез в качестве
моделей предельных распределений статистик в случае ошибок наблюдений отклика,
подчиняющихся законам распределения Коши и экспоненциальному семейству с
параметрами формы l=0.5, l=1.0 (соответствует
распределению Лапласа), l=2.0 (соответствует нормальному закону), l=3.0, l=10.0. В случае логистического закона ошибок наблюдений
в качестве предельного распределения статистики (6), как и в «классическом»
случае, может использоваться распределение Фишера 
.
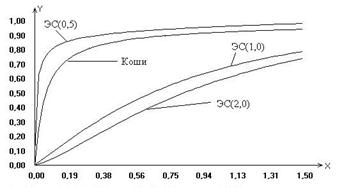
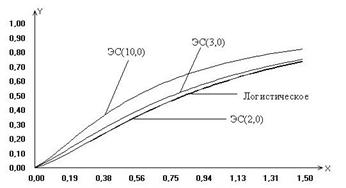
Рис. 1 Рис. 2
На рисунках 1 и 2 в качестве иллюстрации представлены построенные в результате исследований модели предельных распределений статистики (6), соответствующие различным законам распределения ошибок наблюдений.
Рассматривая
полученные модели распределений статистик, можно сделать вывод, что незначительные
отклонения закона распределения ошибок наблюдений отклика от нормального (как в
случае логистического закона распределения) не влияют значимо на предельное
распределение исследуемой статистики. В то же время для моделей регрессии с
ошибками наблюдений, подчиняющимися законам распределения, сильно отличающимся
по свойствам от нормального (Коши, ЭС при
и т.п.), распределения статистики (6)
также сильно отличаются от «классического» предельного распределения 
.
Для того чтобы
можно было сравнить результаты исследований задач дисперсионного анализа с
результатами, приведенными выше для регрессионного анализа, была рассмотрена
нетипичная для дисперсионного анализа модель с невырожденной матрицей 
, которая допускает
проверку гипотезы, аналогичной по форме гипотезе (5). Матрица является невырожденной,
когда матрица планирования является матрицей полного столбцового
ранга, что справедливо для модели вида [2]:
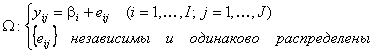(7)
В этом случае 
, 
, 
, 
. При проведении
исследований использовалась модель вида (7) размерности 
, имеющая ранг матрицы планирования
, 
, 
. При всех
перечисленных характеристиках модели (7) распределение статистики (3) для
проверки гипотезы вида (5) в случае нормально распределенной ошибки наблюдений
будет подчиняться распределению Фишера 
.
На рис. 3-4
приведены построенные приближения предельных законов распределений статистики
(3) для проверки гипотезы вида (5) на примере модели (7) в случаях, когда закон
распределения ошибок наблюдения описывается распределением Коши, логистическим
или экспоненциальным семейством с различными параметрами формы . На рис. 3 – при
значениях параметра l=0.5, l=1.0, l=2.0
(l=2.0 случай «классического»
нормального распределения ошибки), на рис. 4 – при значениях параметра l=2.0, l=3.0,
l=10.0. Из рис. 3 легко заметить, что
при уменьшении параметра формы l закона
распределения ошибок наблюдений, приближенные предельные распределения
статистик удаляются, “поднимаясь” от предельного распределения статистики в
случае нормального распределения ошибок. Случай, когда ошибки наблюдений
подчинены закону Коши, соответствует предельному для экспоненциального
семейства при l
. Распределение статистики
(3) при ошибках, подчиняющихся распределению Коши, является, как это можно
увидеть по рис. 3, некоторым пределом распределений статистик для моделей, с
ошибками наблюдений, подчиняющимися распределениям экспоненциального семейства
при l. Результаты исследований,
представленные на рис. 3, позволяют говорить о том, что отклонения закона
распределения ошибок от нормального в сторону распределений с “тяжелыми хвостами”
(в рамках экспоненциального семейства при уменьшении параметра формы) очень
быстро приводят к существенным отклонениям распределения статистики от
классического предельного F-распределения Фишера.
Вид функций распределения статистики (3), представленных на рис. 4, показывает, что при увеличении параметра формы распределения экспоненциального семейства ошибок наблюдения приближенные предельные распределения статистик также, “поднимаясь”, удаляются, хотя, может быть, и не с такой скоростью как в случае уменьшения параметра формы, от предельного распределения статистики, соответствующего случаю нормального распределения ошибок. Представленный здесь также случай логистического распределения ошибок наблюдения, которое интересно тем, что по своим свойствам очень близко к нормальному, позволяет сделать вывод о том, что если распределения ошибок наблюдения близко к нормальному, то и предельное распределение статистики будет близко к классическому F-распределению Фишера.
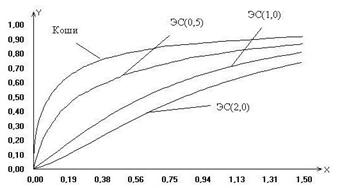
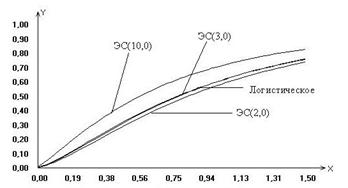
Рис. 3 Рис. 4
В целом,
сравнивая результаты исследований на регрессионных и дисперсионных моделях вида
(7), которые проводились независимо, можно отметить схожее поведение
распределений статистик. Существенные различия были заметны в поведении
предельного распределения статистики в случае распределения ошибок наблюдений,
подчиняющихся закону Коши, по отношению к поведению предельного распределения
статистики в случае ошибок наблюдений, распределенных в соответствии
экспоненциальным семейством при l. Отмечено было
также различие в степени близости предельного распределения статистики (в
дисперсионном и регрессионном анализе) при логистическом распределении ошибок по
отношению к классическому предельному распределению.
Далее была
предпринята попытка выяснить, будут ли результаты, приводимые выше, различаться
с результатами, которые могут быть получены для классической модели
дисперсионного анализа – модели с вырожденной матрицей . Вопрос влияния отклонения
распределения ошибок наблюдений от нормального на предельное распределение
статистики (3) был исследован на примере модели вида
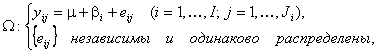(8)
которая отличается от модели (7)
тем, что в векторе параметров появляется еще один элемент – аддитивная
постоянная 
,
а в матрице планирования – дополнительный, соответствующий , столбец из единиц.
В этой модели 
,
, , , . В силу вырожденности
матрицы гипотеза
вида (5) в такой модели не проверяема. Такая ситуация характерна для
дисперсионного анализа, в рамках которого широко применяется проверка гипотез,
основанных на ФДО (функциях, допускающих оценивание). С определением последних
и видами гипотез, формируемых на их основе, можно познакомиться в [2]. При
проведении исследований мы проверяем гипотезу вида
, (9)
где 
и 
- некоторые известные значения ФДО 
и 
.
При проверке этой гипотезы распределение статистики (3) в случае нормально
распределенной ошибки наблюдений будет подчиняться закону распределения Фишера 
. На рис. 5 и рис. 6
приведены данные, полученные для модели (8) при проверке гипотезы (9),
аналогичные тем, что были приведены на рис. 3 и рис. 4 для модели (7) при
проверке гипотезы (5). Сравнительный анализ рис. 3 и рис. 5, рис. 4 и рис. 6 позволяет
говорить о том, что вырожденность матрицы не приводит, по крайней мере, в случае
рассмотренных моделей, к каким-либо существенным изменениям в характере
поведения предельных распределений статистик при отклонении ошибки наблюдений
от нормального закона.
В целом сравнение результатов, полученных в рамках регрессионного и дисперсионного анализа для моделей, в которых ошибка наблюдений подчиняется двустороннему экспоненциальному закону распределения с различными значениями параметра формы, позволило выявить общие тенденции. Полученное в результате моделирования приближение предельного распределения статистики (3) при параметре формы двустороннего экспоненциального закона l = 2 совпадает с предельной функцией распределения статистики для “классического” случая. В данном случае при проверке согласия получаемых в результате моделирования эмпирических распределений статистик с предельным “классическим” F-распределением Фишера всегда достигался очень высокий уровень значимости по всем применяемым критериям согласия [9,10]. Самое “высокое” (на рисунках) из рассмотренных приближений предельных функций распределения статистик получается при значении параметра l=0,5 (из рассмотренных). Далее с ростом значения параметра l вплоть до l = 2, приближенные функции распределения “спускаются” к предельному закону, справедливому для “классической” регрессии. При дальнейшем росте значения параметра формы, приближенные функции распределения статистики “поднимаются” от предельного закона, справедливого для статистики критерия при нормальных ошибках наблюдений.
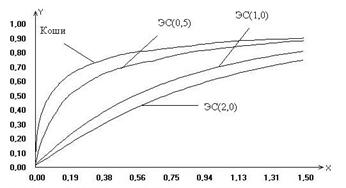
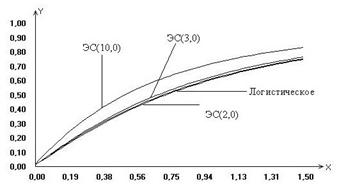
Рис. 5 Рис. 6
Проведенные исследования показали перспективность применения методики компьютерного исследования статистических закономерностей в задачах регрессионного и дисперсионного анализа. Исследования показали возможность построения простых аналитических моделей для распределений статистик, используемых при проверке статистических гипотез в регрессионном и дисперсионном анализе. Часто хорошей моделью для распределений статистик, используемых в регрессионном и дисперсионном анализах, оказывается бета-распределение II-го рода. Построены модели распределений статистик для ряда законов распределений ошибок отклика при различных регрессионных моделях.
1. Демиденко Е.З. Линейная и нелинейная регрессия. – М.: Финансы и статистика, 1981. – 302 с.
2. Шеффе Г. Дисперсионный анализ. – М.: Физматгиз, 1963.
5. Лемешко Б.Ю., Постовалов С.Н. Применение непараметрических критериев согласия при проверке сложных гипотез // Автометрия. 2001. – № 2. – С. 88-102.
6. Лемешко Б.Ю., Трушина Е.В. Исследование вопросов проверки статистических гипотез в линейном регрессионном анализе // Тезисы докладов региональной НТК "Наука. Техника. Инновации" (НТИ-2001), 2001. – Т.2. – С.36-37.
8. Лемешко Б.Ю., Трушина Е.В. Исследование влияния законов распределения ошибок на распределения статистик в линейном регрессионном анализе // Материалы международной НТК "Информатика и проблемы телекоммуникаций". – Новосибирск, 2002. – С. 124-125.