Метрология. 2009. № 4. – С. 3-24
УДК 519.233.3: 006.91.001
ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ И МОЩНОСТИ НЕКОТОРЫХ КРИТЕРИЕВ НОРМАЛЬНОСТИ
Б.Ю. Лемешко, А.П. Рогожников
4. Критерий Дэвида-Хартли-Пирсона
Дополнительные
ссылки:
Лемешко
Б.Ю., Лемешко С.Б. Сравнительный
анализ критериев проверки отклонения распределения от нормального закона //
Метрология. 2005. № 2. – С. 3-24.
Лемешко Б.Ю., Рогожников А.П. О нормальности погрешностей измерений в
классических экспериментах и мощности критериев, применяемых для проверки
отклонения от нормального закона // Метрология. 2012. № 5. – С. 3-26.
См. также: Прикладная математическая статистика (материалы к семинарам)
Исследованы достоинства и недостатки, оценена мощность различных критериев проверки отклонения от нормального закона (критериев Фросини, Хегази-Грина, Шпигельхальтера, Гири и Дэвида-Хартли-Пирсона).
Ключевые слова: мощность критерия, критерий Фросини, критерии Хегази-Грина, критерий Шпигельхальтера, критерий Гири, критерий Дэвида-Хартли-Пирсона.
Введение
В силу объективных причин проверка на отклонение от нормального закона является частой процедурой в ходе проведения измерений, контроля и испытаний. После выхода стандарта [1] в работе [2] был проведен сравнительный анализ ряда статистических критериев, предназначенных для проверки отклонения эмпирических распределений от нормального закона, в ходе которого были проанализированы мощность и выявлены недостатки отдельных критериев, ранее не упоминаемые в литературе. В данной статье продолжен анализ, начатый в работе [2]. Перечень критериев, исследованных в [2], расширен за счет критериев Фросини [3,4], Хегази-Грина [5], Шпигельхальтера [6], Гири [7] и Дэвида-Хартли-Пирсона [8]. Свойства и мощность данных критериев сравниваются со свойствами ранее проанализированных в работе [2]. Даются рекомендации о целесообразности применения тех или иных критериев.
В настоящей работе при
сравнительном анализе мощности критериев рассматривались те же конкурирующие
гипотезы, что и в [2]. Проверяемой гипотезе 
соответствует нормальный
закон с плотностью 
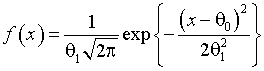(1)
с параметром масштаба 
и параметром сдвига 
. В качестве конкурирующей гипотезы 
рассмотрено распределение
семейства
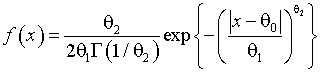(2)
с параметром формы 
, параметром масштаба и параметром сдвига ; в качестве конкурирующей гипотезы 
– распределение семейства (2)
с параметром формы 
(распределение Лапласа), параметрами масштаба и сдвига ; конкурирующей гипотезе 
соответствует логистическое распределение с плотностью
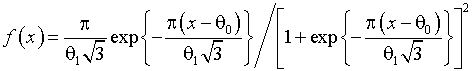(3)
с параметрами и .
На рисунке 1 приведены плотности распределений, соответствующие каждой из
гипотез
.
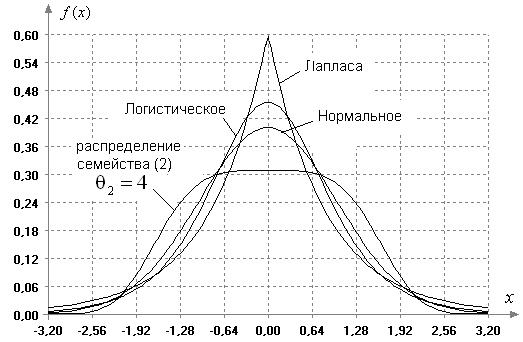
Рис. 1. Распределения, соответствующие рассматриваемым
гипотезам 
.
При исследовании
распределений, построении процентных точек статистик критериев и оценке
мощности критериев относительно различных конкурирующих гипотез в данной
работе использовалась методика статистического моделирования [9]. При этом количество
испытаний (объем выборок моделируемых распределений статистик), как правило,
выбирался равным 
, что позволяло оценивать
соответствующие вероятности с погрешностью в пределах ±10-3.
Для проверки отклонения
эмпирического распределения от нормального закона можно применять критерии
согласия (непараметрические и типа 
). Кажется естественным предполагать,
что критерии, специально предназначенные для проверки отклонения от
нормального закона, достаточно широкий перечень
которых приведен в [10], должны обладать определенными преимуществами в
мощности. Действительно, при малых объемах выборок такие преимущества, как
правило, наблюдаются.
Но не всё так безоблачно.
Исследования, проведенные в [2], показали, что популярные критерии Шапиро-Уилка и Эппса-Палли,
рекомендуемые стандартом [1], при малых объемах выборок и малых уровнях
значимости 
(вероятностях ошибки первого рода) являются смещенными,
например, относительно конкурирующей гипотезы (мощность критериев оказывается
меньше величины уровня значимости). И, как увидим ниже, подобными серьезными
недостатками обладают и некоторые другие критерии, свойства которых исследованы
в данной работе.
1.
Критерий Фросини
Статистика критерия Фросини [3,4] имеет вид
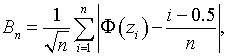(4)
где элементы выборки 
, 
, упорядочены по возрастанию,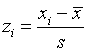 
, 
, 
, 
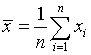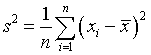– функция распределения стандартного
нормального закона 
.
Применение критерия
осложняется тем, что условные распределения 
статистики критерия Фросини при справедливости проверяемой гипотезы зависят от объемов выборок 
. Характер этой зависимости иллюстрирует
рисунок 2. С ростом распределения статистики смещаются вправо и достаточно быстро сходятся к некоторому
предельному распределению. При объемах выборок 
распределения
статистики уже существенно не меняются.
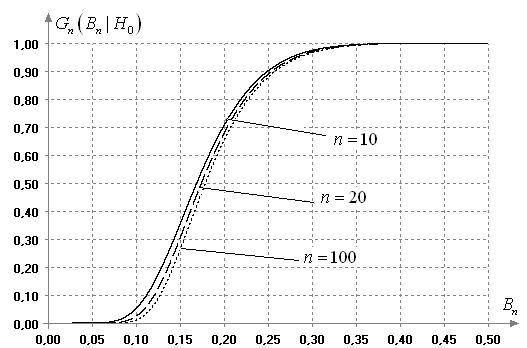
Рис.2. Зависимость
распределения 
статистики
от
объема выборки
Полученная в [4] таблица
процентных точек для распределений статистики Фросини
наиболее доступна в [10]. Гипотеза о принадлежности выборки нормальному закону
отклоняется при больших значениях статистики. В таблице 1 представлены значения
процентных точек для статистики критерия Фросини,
полученные в данной работе и расширяющие таблицы, приводимые в [4, 10], на
большие значения объемов выборок 
.
Таблица 1. Процентные точки для статистик критерия Фросини.
|
n |
|
||||
|
0.85 |
0.9 |
0.95 |
0.975 |
0.99 |
|
|
10 |
0.233 |
0.250 |
0.277 |
0.302 |
0.332 |
|
20 |
0.237 |
0.255 |
0.283 |
0.308 |
0.338 |
|
30 |
0.239 |
0.257 |
0.284 |
0.310 |
0.342 |
|
40 |
0.239 |
0.257 |
0.285 |
0.310 |
0.342 |
|
50 |
0.240 |
0.258 |
0.285 |
0.312 |
0.342 |
|
100 |
0.241 |
0.258 |
0.286 |
0.312 |
0.344 |
|
150 |
0.241 |
0.259 |
0.287 |
0.313 |
0.345 |
|
200 |
0.241 |
0.259 |
0.287 |
0.313 |
0.345 |
|
300 |
0.242 |
0.259 |
0.288 |
0.314 |
0.345 |
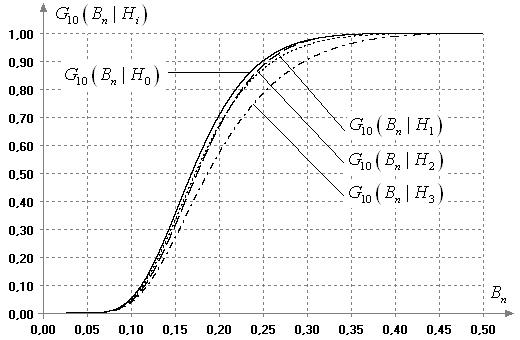
Рис. 3. Условные
распределения 
статистики
при
объеме выборок n=10
На рис. 3 приведены
графики распределения статистики 
при справедливости различных
гипотез (при различных наблюдаемых законах) для объемов выборок 
, которые позволяют судить о мощности
критерия относительно рассматриваемых конкурирующих гипотез. Значения мощности
критерия Фросини относительно конкурирующей гипотезы
приведены в таблице 2, а
мощности критерия по отношению к гипотезам и – в таблицах 3 и 4
соответственно.
У критерия Фросини отсутствует недостаток, свойственный при
малых (n ≤ 20) критериям Шапиро-Уилка
и Эппса-Палли по отношению к конкурирующей гипотезе [2]. Однако он обладает не
очень высокой мощностью и, в частности, уступает по мощности критериям
согласия Андерсона-Дарлинга и типа 
Никулина.
Таблица 2.
Значения мощности критерия Фросини относительно
гипотезы 
.
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.175 |
0.117 |
0.057 |
0.027 |
0.010 |
|
20 |
0.224 |
0.155 |
0.080 |
0.041 |
0.016 |
|
30 |
0.273 |
0.197 |
0.109 |
0.057 |
0.023 |
|
40 |
0.325 |
0.242 |
0.140 |
0.078 |
0.034 |
|
50 |
0.376 |
0.286 |
0.173 |
0.099 |
0.046 |
|
100 |
0.602 |
0.506 |
0.361 |
0.245 |
0.138 |
|
150 |
0.768 |
0.689 |
0.548 |
0.416 |
0.270 |
|
200 |
0.874 |
0.817 |
0.702 |
0.577 |
0.421 |
|
300 |
0.969 |
0.947 |
0.892 |
0.817 |
0.694 |
Таблица 3. Значения мощности критерия Фросини относительно гипотезы 
.
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.278 |
0.216 |
0.141 |
0.093 |
0.053 |
|
20 |
0.407 |
0.336 |
0.242 |
0.175 |
0.113 |
|
30 |
0.515 |
0.442 |
0.339 |
0.257 |
0.176 |
|
40 |
0.611 |
0.540 |
0.432 |
0.342 |
0.247 |
|
50 |
0.689 |
0.623 |
0.517 |
0.421 |
0.319 |
|
100 |
0.911 |
0.879 |
0.816 |
0.745 |
0.647 |
|
150 |
0.978 |
0.967 |
0.941 |
0.907 |
0.850 |
|
200 |
0.995 |
0.992 |
0.983 |
0.970 |
0.945 |
|
300 |
1.000 |
1.000 |
0.999 |
0.998 |
0.995 |
Таблица 4. Значения мощности критерия Фросини относительно гипотезы 
.
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.183 |
0.130 |
0.072 |
0.041 |
0.019 |
|
20 |
0.212 |
0.154 |
0.090 |
0.054 |
0.028 |
|
30 |
0.234 |
0.174 |
0.106 |
0.065 |
0.034 |
|
40 |
0.257 |
0.194 |
0.121 |
0.075 |
0.040 |
|
50 |
0.277 |
0.211 |
0.134 |
0.085 |
0.047 |
|
100 |
0.373 |
0.299 |
0.204 |
0.138 |
0.081 |
|
150 |
0.461 |
0.383 |
0.274 |
0.194 |
0.120 |
|
200 |
0.540 |
0.460 |
0.344 |
0.252 |
0.165 |
|
300 |
0.672 |
0.598 |
0.479 |
0.375 |
0.265 |
2.
Критерии Хегази-Грина
Хегази и Грин в [5] предложили критерии со статистиками
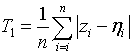, (5)
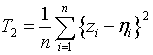, (6)
где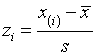 
, , 
, 
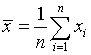– математическое ожидание 
-й порядковой статистики стандартного
нормального закона, которое можно найти из соотношения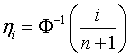 
. Проверяемая гипотеза отклоняется
при больших значениях статистик. Подчеркнем, что в статистике должна
использоваться именно несмещенная оценка дисперсии, это не учтено в [10].
Распределения этих
статистик очень сильно зависят от объема выборки. Например, зависимость
условных распределений 
статистики 
от иллюстрирует рисунок 4.
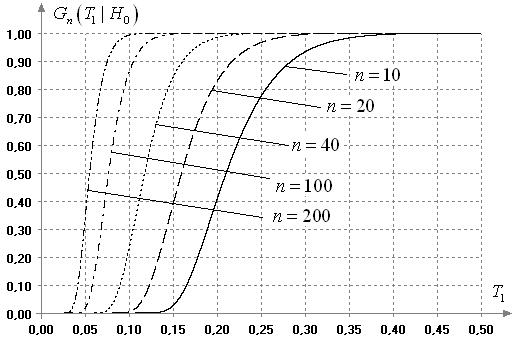
Рис.4. Зависимость
распределений статистики 
от
объема выборки
Таблицы процентных точек
для данных критериев при некоторых объемах выборок приводятся в [5, 10]. В таблице
5 представлены процентные точки для статистик и 
критерия Хегази-Грина,
полученные в данной работе и расширяющие таблицы, приведенные в [5, 10].
Таблица 5.
Процентные точки для статистик и
критерия
Хегази-Грина
|
|
|
|||||||||
|
|
|
|||||||||
|
0.85 |
0.9 |
0.95 |
0.975 |
0.99 |
0.85 |
0.9 |
0.95 |
0.975 |
0.99 |
|
|
10 |
0.268 |
0.285 |
0.312 |
0.338 |
0.370 |
0.112 |
0.127 |
0.153 |
0.180 |
0.216 |
|
20 |
0.205 |
0.218 |
0.239 |
0.259 |
0.284 |
0.072 |
0.082 |
0.100 |
0.118 |
0.143 |
|
40 |
0.151 |
0.161 |
0.177 |
0.191 |
0.210 |
0.043 |
0.049 |
0.060 |
0.070 |
0.085 |
|
60 |
0.126 |
0.134 |
0.147 |
0.159 |
0.174 |
0.031 |
0.035 |
0.043 |
0.050 |
0.061 |
|
80 |
0.110 |
0.117 |
0.128 |
0.139 |
0.152 |
0.024 |
0.028 |
0.033 |
0.039 |
0.047 |
|
100 |
0.099 |
0.105 |
0.115 |
0.125 |
0.137 |
0.020 |
0.023 |
0.028 |
0.032 |
0.039 |
|
200 |
0.071 |
0.075 |
0.083 |
0.090 |
0.098 |
0.011 |
0.012 |
0.015 |
0.017 |
0.021 |
|
300 |
0.058 |
0.062 |
0.068 |
0.073 |
0.080 |
0.008 |
0.009 |
0.010 |
0.012 |
0.014 |
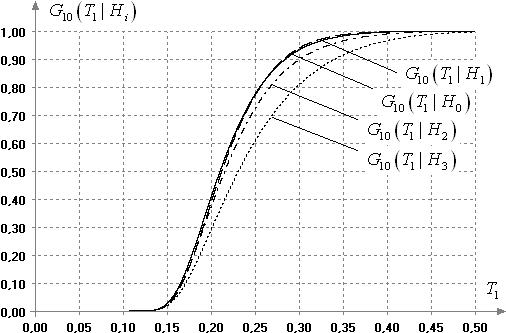
Рис. 5. Условные
распределения 
статистики
при
справедливости гипотез при объеме выборок 
На рисунке 5 показаны
условные функции распределения 
статистики при справедливости гипотез , , , при объемах выборок . При и 
критерий практически не
различает гипотезы и (аналогично критериям Шапиро-Уилка
и Эппса-Палли он оказывается смещённым). Но, уже при 
для всех задаваемых уровней
значимости критерий способен различать эти конкурирующие гипотезы.
На рисунке 6 приведены
условные функции распределения 
статистики при справедливости гипотез , , , при объемах выборок . Как видим, относительно
конкурирующей гипотезы этот критерий также оказывается смещенным. Распределение
смещено влево относительно
распределения 
, и, следовательно, при справедливости критерий с большей уверенностью
признает истинность .
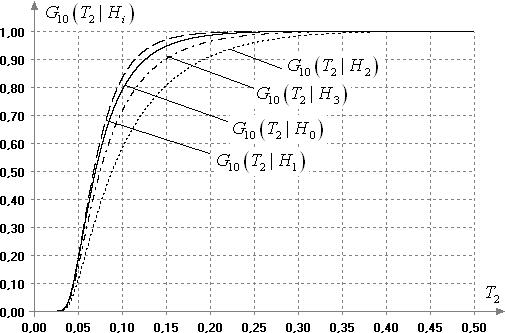
Рис. 6. Условные
распределения 
статистики
при
справедливости гипотез при объеме выборок
Полученные оценки
значений мощности критериев Хегази-Грина относительно
рассмотренных альтернатив , , приведены в таблицах 6-8.
Оба критерия Хегази-Грина демонстрируют более высокую мощность по сравнению
с критериями Шапиро-Уилка и Эппса-Палли
относительно конкурирующих гипотез и . Однако по отношению к гипотезам
типа при малых объёмах выборок оба критерия оказываются
смещенными, особенно критерий со статистикой (смещение даже больше, чем у
критериев Шапиро-Уилка и Эппса-Палли).
Таблица 6. Значения мощности критериев Хегази-Грина относительно гипотезы
|
|
|
|||||||||
|
|
|
|||||||||
|
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.148 |
0.095 |
0.043 |
0.019 |
0.007 |
0.110 |
0.067 |
0.028 |
0.012 |
0.004 |
|
20 |
0.172 |
0.112 |
0.052 |
0.023 |
0.008 |
0.085 |
0.046 |
0.016 |
0.006 |
0.001 |
|
40 |
0.253 |
0.176 |
0.090 |
0.044 |
0.016 |
0.095 |
0.050 |
0.016 |
0.005 |
0.001 |
|
60 |
0.352 |
0.261 |
0.148 |
0.079 |
0.032 |
0.137 |
0.077 |
0.026 |
0.008 |
0.001 |
|
80 |
0.455 |
0.356 |
0.221 |
0.129 |
0.058 |
0.198 |
0.119 |
0.045 |
0.015 |
0.003 |
|
100 |
0.552 |
0.450 |
0.302 |
0.191 |
0.096 |
0.271 |
0.175 |
0.075 |
0.028 |
0.006 |
|
200 |
0.877 |
0.818 |
0.700 |
0.570 |
0.402 |
0.680 |
0.562 |
0.370 |
0.219 |
0.093 |
|
300 |
0.976 |
0.959 |
0.912 |
0.843 |
0.723 |
0.913 |
0.854 |
0.720 |
0.561 |
0.352 |
Таблица 7. Значения мощности критериев Хегази-Грина относительно гипотезы
|
|
|
|||||||||
|
|
|
|||||||||
|
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.307 |
0.242 |
0.161 |
0.106 |
0.060 |
0.347 |
0.277 |
0.185 |
0.123 |
0.071 |
|
20 |
0.454 |
0.382 |
0.282 |
0.207 |
0.135 |
0.517 |
0.441 |
0.332 |
0.247 |
0.165 |
|
40 |
0.661 |
0.594 |
0.486 |
0.392 |
0.290 |
0.718 |
0.651 |
0.542 |
0.443 |
0.332 |
|
60 |
0.793 |
0.740 |
0.646 |
0.554 |
0.441 |
0.832 |
0.781 |
0.688 |
0.596 |
0.480 |
|
80 |
0.877 |
0.838 |
0.764 |
0.685 |
0.580 |
0.900 |
0.863 |
0.791 |
0.712 |
0.605 |
|
100 |
0.928 |
0.901 |
0.846 |
0.783 |
0.693 |
0.941 |
0.915 |
0.862 |
0.799 |
0.705 |
|
200 |
0.996 |
0.994 |
0.987 |
0.976 |
0.955 |
0.996 |
0.993 |
0.986 |
0.973 |
0.948 |
|
300 |
1.000 |
1.000 |
0.999 |
0.998 |
0.996 |
1.000 |
1.000 |
0.999 |
0.997 |
0.993 |
Таблица 8. Значения мощности критериев Хегази-Грина относительно гипотезы
|
|
|
|||||||||
|
|
|
|||||||||
|
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.197 |
0.141 |
0.081 |
0.047 |
0.022 |
0.219 |
0.160 |
0.093 |
0.055 |
0.027 |
|
20 |
0.241 |
0.180 |
0.111 |
0.068 |
0.036 |
0.291 |
0.225 |
0.146 |
0.095 |
0.053 |
|
40 |
0.307 |
0.240 |
0.158 |
0.103 |
0.059 |
0.393 |
0.321 |
0.225 |
0.158 |
0.099 |
|
60 |
0.362 |
0.291 |
0.198 |
0.135 |
0.081 |
0.469 |
0.394 |
0.290 |
0.213 |
0.140 |
|
80 |
0.411 |
0.337 |
0.238 |
0.167 |
0.104 |
0.530 |
0.455 |
0.347 |
0.262 |
0.181 |
|
100 |
0.456 |
0.380 |
0.275 |
0.198 |
0.127 |
0.581 |
0.508 |
0.399 |
0.310 |
0.218 |
|
200 |
0.638 |
0.564 |
0.451 |
0.353 |
0.249 |
0.760 |
0.699 |
0.598 |
0.504 |
0.394 |
|
300 |
0.765 |
0.703 |
0.597 |
0.497 |
0.380 |
0.861 |
0.817 |
0.736 |
0.653 |
0.544 |
3. Критерий Гири
Гири в работах [7, 11, 12] рассмотрел критерий проверки отклонения от нормального закона, основанный на статистике
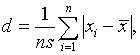(7)
где 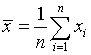, 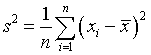. Критерий является двусторонним, и
гипотеза о нормальности не отклоняется, если 
.
Зависимость условных распределений 
статистики (7) от иллюстрирует рисунок 7.
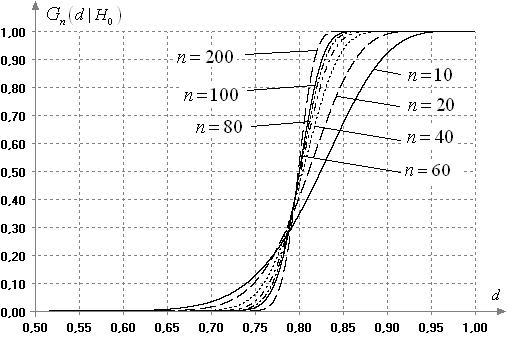
Рис. 7. Зависимость
распределений статистики 
от
объема выборки
Автором критерия
утверждается, что статистика критерия при 
распределена асимптотически
нормально. Выражения для математического ожидания и дисперсии асимптотического
закона представлены, например, в [10]. Однако на самом деле распределения
статистики асимметричны и плохо аппроксимируются
нормальным законом, тем более с указанными в [10] параметрами.
Таблицы процентных точек
для некоторых объемов выборок приводятся в [7]. В таблице 9 представлены
процентные точки 
и 
статистики критерия Гири, полученные в данной работе.
Эти результаты расширяют область применения критерия.
Таблица 9. Процентные точки для статистики критерия Гири
|
|
|
|||||||||
|
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
||||||
|
α/2 |
1- α/2 |
α/2 |
1- α/2 |
α/2 |
1- α/2 |
α/2 |
1- α/2 |
α/2 |
1- α/2 |
|
|
10 |
0.729 |
0.902 |
0.715 |
0.911 |
0.691 |
0.924 |
0.670 |
0.935 |
0.644 |
0.948 |
|
20 |
0.741 |
0.870 |
0.730 |
0.878 |
0.713 |
0.889 |
0.697 |
0.899 |
0.678 |
0.910 |
|
40 |
0.754 |
0.848 |
0.747 |
0.854 |
0.735 |
0.863 |
0.724 |
0.871 |
0.710 |
0.879 |
|
60 |
0.761 |
0.839 |
0.755 |
0.844 |
0.746 |
0.851 |
0.737 |
0.858 |
0.726 |
0.865 |
|
80 |
0.766 |
0.833 |
0.761 |
0.838 |
0.752 |
0.844 |
0.745 |
0.850 |
0.736 |
0.857 |
|
100 |
0.769 |
0.829 |
0.764 |
0.833 |
0.757 |
0.839 |
0.750 |
0.845 |
0.742 |
0.851 |
|
200 |
0.777 |
0.820 |
0.774 |
0.823 |
0.769 |
0.827 |
0.764 |
0.831 |
0.759 |
0.836 |
На рис. 8 показаны
условные функции распределения 
статистики 
при справедливости гипотез , , , при объеме выборок . Проверяемая гипотеза отклоняется
при значениях статистики, меньших и больших .
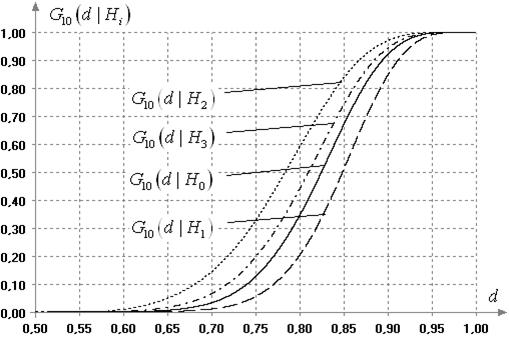
Рис. 8. Условные
распределения 
статистики
критерия
Гири при справедливости различных гипотез и объёме выборок
Полученные значения
оценок мощности относительно конкурирующих гипотез , , представлены в таблицах 10-12.
Критерий Гири с простой статистикой (7) достаточно уверенно демонстрирует
высокую мощность к различным конкурирующим гипотезам.
Таблица 10. Значения мощности критерия Гири
относительно конкурирующей гипотезы
|
|
|
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,174 |
0,120 |
0,064 |
0,034 |
0,014 |
|
20 |
0,247 |
0,181 |
0,105 |
0,061 |
0,029 |
|
40 |
0,409 |
0,326 |
0,215 |
0,138 |
0,075 |
|
60 |
0,546 |
0,457 |
0,328 |
0,228 |
0,136 |
|
80 |
0,662 |
0,577 |
0,441 |
0,328 |
0,211 |
|
100 |
0,750 |
0,674 |
0,544 |
0,424 |
0,294 |
|
200 |
0,953 |
0,927 |
0,866 |
0,790 |
0,669 |
Таблица 11. Значения мощности критерия Гири
относительно конкурирующей гипотезы
|
|
|
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,267 |
0,204 |
0,130 |
0,082 |
0,043 |
|
20 |
0,442 |
0,371 |
0,274 |
0,201 |
0,132 |
|
40 |
0,694 |
0,630 |
0,528 |
0,435 |
0,330 |
|
60 |
0,838 |
0,792 |
0,709 |
0,625 |
0,519 |
|
80 |
0,917 |
0,888 |
0,829 |
0,764 |
0,671 |
|
100 |
0,958 |
0,940 |
0,902 |
0,855 |
0,784 |
|
200 |
0,999 |
0,998 |
0,996 |
0,992 |
0,983 |
Таблица 12. Значения мощности критерия Гири относительно
конкурирующей гипотезы
|
|
|
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,182 |
0,127 |
0,069 |
0,038 |
0,017 |
|
20 |
0,227 |
0,169 |
0,103 |
0,063 |
0,033 |
|
40 |
0,305 |
0,240 |
0,161 |
0,108 |
0,064 |
|
60 |
0,372 |
0,303 |
0,214 |
0,151 |
0,096 |
|
80 |
0,431 |
0,361 |
0,266 |
0,195 |
0,128 |
|
100 |
0,486 |
0,415 |
0,313 |
0,235 |
0,160 |
|
200 |
0,695 |
0,631 |
0,527 |
0,433 |
0,329 |
4. Критерий Дэвида-Хартли-Пирсона
В критерии Дэвида-Хартли-Пирсона [8] рассматривается отношение размаха выборки к выборочному стандартному отклонению, и его статистика имеет вид:
,
(8)
где 
- размах выборки, - несмещённая оценка дисперсии.
Рисунок 9 иллюстрирует зависимость
распределений статистики 
от объёма выборки при справедливости проверяемой
гипотезы.
Рис. 9. Зависимость распределений статистики 
от объема выборки
Критерий двусторонний: гипотеза
о нормальности распределения отвергается, если 
или 
. В таблице 13 приведены процентные
точки критерия Дэвида-Хартли-Пирсона для объёмов выборок, использованных в
данной работе.
Таблица 13. Процентные точки
для статистики критерия
Дэвида-Хартли-Пирсона
|
|
0.15 |
0,1 |
0,05 |
0,025 |
0,01 |
|||||
|
a/2 |
1-a/2 |
a/2 |
1-a/2 |
a/2 |
1-a/2 |
a/2 |
1-a/2 |
a/2 |
1-a/2 |
|
|
10 |
2,723 |
3,624 |
2,670 |
3,686 |
2,593 |
3,778 |
2,530 |
3,854 |
2,458 |
3,936 |
|
20 |
3,240 |
4,392 |
3,178 |
4,488 |
3,087 |
4,633 |
3,012 |
4,763 |
2,927 |
4,915 |
|
40 |
3,741 |
5,046 |
3,674 |
5,162 |
3,574 |
5,345 |
3,493 |
5,507 |
3,401 |
5,708 |
|
60 |
4,028 |
5,384 |
3,958 |
5,508 |
3,856 |
5,704 |
3,769 |
5,886 |
3,674 |
6,106 |
|
80 |
4,230 |
5,607 |
4,158 |
5,735 |
4,054 |
5,937 |
3,967 |
6,124 |
3,870 |
6,354 |
|
100 |
4,382 |
5,774 |
4,311 |
5,905 |
4,206 |
6,112 |
4,117 |
6,302 |
4,018 |
6,536 |
|
200 |
4,847 |
6,255 |
4,774 |
6,388 |
4,668 |
6,600 |
4,578 |
6,799 |
4,474 |
7,044 |
На рисунке 10 показаны
условные распределения 
статистики при справедливости гипотез , , , при объемах выборок .
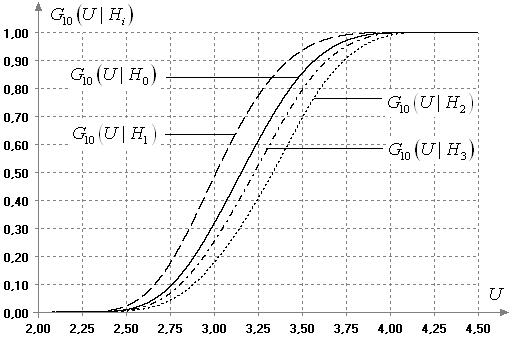
Рис. 10. Условные
распределения 
статистики
при
справедливости различных гипотез при объемах выборок .
Полученные оценки
мощности для рассматриваемых конкурирующих гипотез приведены в таблицах 14-16.
Его мощность относительно практически совпадает с мощностью критерия Гири, однако
он существенно уступает последнему по отношению к конкурирующим гипотезам и .
Таблица 14. Значения мощности критерия
Дэвида-Хартли-Пирсона относительно конкурирующей гипотезы
|
|
α |
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,176 |
0,121 |
0,064 |
0,034 |
0,014 |
|
20 |
0,251 |
0,185 |
0,107 |
0,061 |
0,028 |
|
40 |
0,417 |
0,332 |
0,217 |
0,140 |
0,075 |
|
60 |
0,552 |
0,461 |
0,327 |
0,224 |
0,132 |
|
80 |
0,658 |
0,569 |
0,428 |
0,314 |
0,199 |
|
100 |
0,734 |
0,655 |
0,519 |
0,396 |
0,264 |
|
200 |
0,919 |
0,878 |
0,793 |
0,694 |
0,554 |
Таблица 15. Значения мощности критерия
Дэвида-Хартли-Пирсона относительно конкурирующей гипотезы
|
|
α |
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,218 |
0,157 |
0,091 |
0,052 |
0,026 |
|
20 |
0,357 |
0,289 |
0,199 |
0,134 |
0,078 |
|
40 |
0,513 |
0,443 |
0,342 |
0,263 |
0,183 |
|
60 |
0,615 |
0,546 |
0,441 |
0,352 |
0,259 |
|
80 |
0,688 |
0,623 |
0,518 |
0,427 |
0,325 |
|
100 |
0,741 |
0,680 |
0,579 |
0,486 |
0,380 |
|
200 |
0,884 |
0,842 |
0,764 |
0,682 |
0,574 |
Таблица 16. Значения мощности критерия
Дэвида-Хартли-Пирсона относительно конкурирующей гипотезы
|
|
α |
||||
|
0,15 |
0,10 |
0,05 |
0,025 |
0,01 |
|
|
10 |
0,168 |
0,114 |
0,059 |
0,031 |
0,013 |
|
20 |
0,220 |
0,161 |
0,094 |
0,054 |
0,026 |
|
40 |
0,291 |
0,228 |
0,150 |
0,101 |
0,059 |
|
60 |
0,345 |
0,279 |
0,194 |
0,135 |
0,084 |
|
80 |
0,391 |
0,322 |
0,232 |
0,167 |
0,108 |
|
100 |
0,429 |
0,359 |
0,264 |
0,195 |
0,130 |
|
200 |
0,566 |
0,494 |
0,390 |
0,304 |
0,217 |
В целом на основании анализа мощности относительно различных конкурирующих гипотез можно констатировать, что критерий Дэвида-Хартли-Пирсона уступает остальным рассмотренным в работе критериям.
5. Критерий Шпигельхальтера
Его статистика [6] базируется на комбинации статистик критериев Гири [7] и Дэвида, Хартли и Пирсона [8] и имеет вид
,
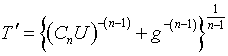(9)
где 
, – статистика (8) критерия
Дэвида-Хартли-Пирсона, 
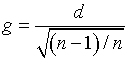, – статистика (7) критерия Гири.
Проверяемая гипотеза о
принадлежности анализируемой выборки нормальному закону по
критерию Шпигельхальтера отклоняется при
больших значениях статистики 
.
Значения процентных точек
для статистики 
критерия Шпигельхальтера, полученные
в результате моделирования, приведены в таблице 17. Зависимость распределения
статистики от объема выборки в случае справедливости проверяемой
гипотезы иллюстрирует рисунок 11.
Таблица 17.
Процентные точки для статистики 
критерия
Шпигельхальтера
|
|
|
||||
|
0.85 |
0.9 |
0.95 |
0.975 |
0.99 |
|
|
10 |
1.323 |
1.344 |
1.380 |
1.416 |
1.460 |
|
20 |
1.311 |
1.331 |
1.365 |
1.396 |
1.435 |
|
30 |
1.300 |
1.318 |
1.346 |
1.373 |
1.406 |
|
40 |
1.293 |
1.308 |
1.332 |
1.355 |
1.383 |
|
50 |
1.288 |
1.302 |
1.323 |
1.342 |
1.366 |
|
100 |
1.279 |
1.288 |
1.302 |
1.314 |
1.329 |
|
150 |
1.275 |
1.283 |
1.294 |
1.304 |
1.315 |
|
200 |
1.273 |
1.279 |
1.289 |
1.297 |
1.307 |
|
300 |
1.270 |
1.275 |
1.283 |
1.289 |
1.297 |
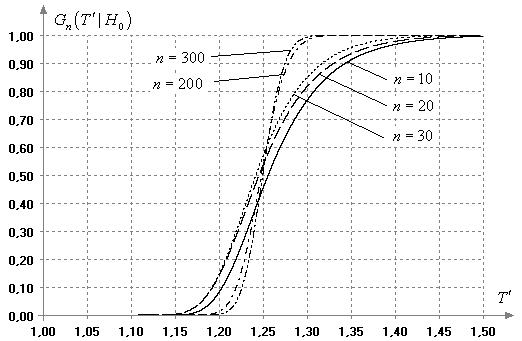
Рис.
11. Зависимость распределения статистики от
объема выборки в случае нормального закона
Однако данный критерий имеет
очень существенный недостаток: критерий со статистикой (9) способен
отличить от нормального закона далеко не все конкурирующие распределения. В
частности, это касается конкурирующей гипотезы 
.
Мощность любого корректно
построенного критерия должна увеличиваться с ростом . В принципе, так и происходит с
мощностью критерия Шпигельхальтера по отношению к
конкурирующим гипотезам и .
Совсем другая картина
наблюдается относительно гипотезы . На рисунках 12-14 показаны
условные функции распределения 
статистики при справедливости гипотез , , , при объемах выборок 
. Можно видеть, что вследствие
специфичного с ростом объема выборок поведения условного распределения 
мощность критерия по отношению
к гипотезе при 
начинает уменьшаться. А далее с
ростом критерий оказывается смещённым относительно
гипотезы и вовсе не способен различать гипотезы и .
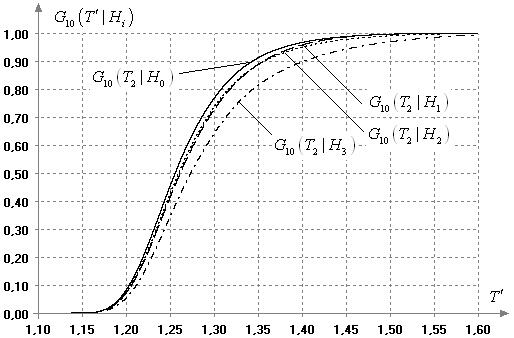
Рис. 12. Условные
распределения 
статистики
при
объеме выборок
Мощность критерия Шпигельхальтера по отношению к гипотезе приведена в таблице 18,
значения мощности по отношению к гипотезам и – в таблицах 19 и 20
соответственно.
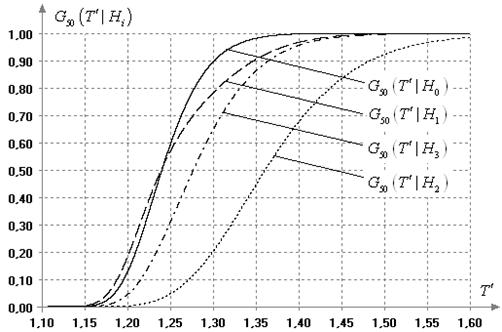
Рис.
13. Условные распределения 
статистики
при
объеме выборок 
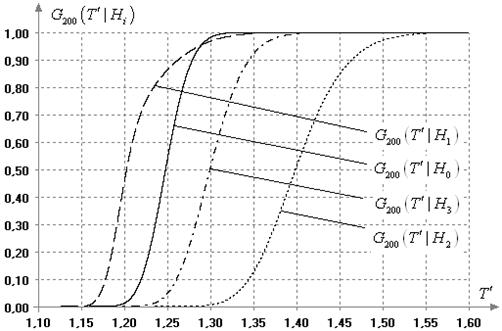
Рис. 14. Условные распределения статистики при объеме выборок 
Таблица 18.
Мощность критерия Шпигельхальтера относительно
гипотезы
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.184 |
0.126 |
0.064 |
0.031 |
0.011 |
|
20 |
0.233 |
0.174 |
0.104 |
0.060 |
0.028 |
|
30 |
0.257 |
0.203 |
0.135 |
0.087 |
0.047 |
|
40 |
0.262 |
0.214 |
0.150 |
0.103 |
0.061 |
|
50 |
0.257 |
0.213 |
0.155 |
0.111 |
0.070 |
|
100 |
0.184 |
0.156 |
0.119 |
0.090 |
0.064 |
|
150 |
0.119 |
0.100 |
0.076 |
0.058 |
0.042 |
|
200 |
0.076 |
0.063 |
0.048 |
0.036 |
0.026 |
|
300 |
0.029 |
0.025 |
0.018 |
0.013 |
0.010 |
Таблица
19. Мощность критерия Шпигельхальтера
относительно гипотезы
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.264 |
0.201 |
0.131 |
0.086 |
0.051 |
|
20 |
0.468 |
0.390 |
0.283 |
0.206 |
0.135 |
|
30 |
0.640 |
0.561 |
0.441 |
0.340 |
0.239 |
|
40 |
0.763 |
0.696 |
0.582 |
0.476 |
0.356 |
|
50 |
0.845 |
0.791 |
0.693 |
0.595 |
0.474 |
|
100 |
0.981 |
0.968 |
0.940 |
0.903 |
0.841 |
|
150 |
0.997 |
0.995 |
0.989 |
0.979 |
0.958 |
|
200 |
1.000 |
0.999 |
0.998 |
0.996 |
0.990 |
|
300 |
1.000 |
1.000 |
1.000 |
1.000 |
1.000 |
Таблица
20. Мощность критерия Шпигельхальтера
относительно гипотезы
|
|
α |
||||
|
0.15 |
0.1 |
0.05 |
0.025 |
0.01 |
|
|
10 |
0.179 |
0.125 |
0.070 |
0.039 |
0.019 |
|
20 |
0.239 |
0.177 |
0.106 |
0.064 |
0.034 |
|
30 |
0.305 |
0.234 |
0.147 |
0.093 |
0.051 |
|
40 |
0.369 |
0.291 |
0.193 |
0.127 |
0.072 |
|
50 |
0.425 |
0.344 |
0.237 |
0.162 |
0.097 |
|
100 |
0.614 |
0.532 |
0.410 |
0.313 |
0.215 |
|
150 |
0.727 |
0.652 |
0.533 |
0.428 |
0.315 |
|
200 |
0.803 |
0.740 |
0.632 |
0.529 |
0.409 |
|
300 |
0.898 |
0.856 |
0.775 |
0.687 |
0.571 |
Заключение
Общим недостатком всех рассмотренных критериев является зависимость распределений статистик от объемов выборок и неизвестность аналитических распределений статистик. Вследствие этого при принятии решения о результатах проверки гипотезы приходится ориентироваться на значения процентных точек, нельзя оценить достигнутый уровень значимости, трудно судить о степени соответствия или несоответствия наблюдаемой выборки нормальному закону.
Результаты проведенного
сравнительного анализа критериев в определенной степени иллюстрирует картина,
представленная на рисунках 15-17, где показана зависимость мощности критериев
от объемов выборок относительно конкурирующих гипотез , и при вероятности ошибки первого
рода 
.
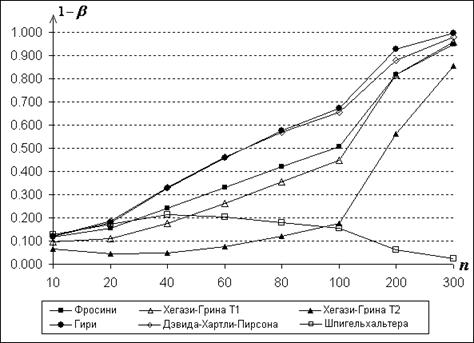
Рис.15. Мощности критериев
по отношению к конкурирующей гипотезе
в зависимости от 
при
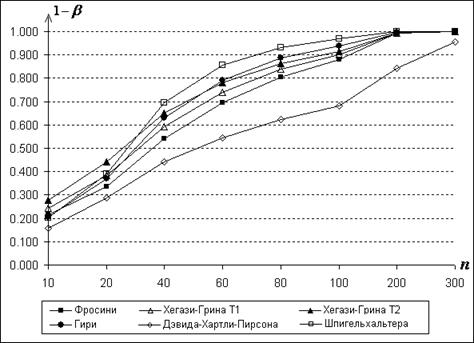
Рис.16. Мощности
критериев по отношению к конкурирующей гипотезе
в зависимости от при
Опираясь на проведенные
исследования свойств рассмотренных критериев и с учетом показанной ими
мощности относительно конкурирующих гипотез , 
, 
данные критерии можно проранжировать по мощности следующим образом:
Гири
Шпигельгалтера1)Хегази-Грина
(
)2)
Хегази-Грина (
)3)
Дэвида-Хартли-Пирсона
Фросини.
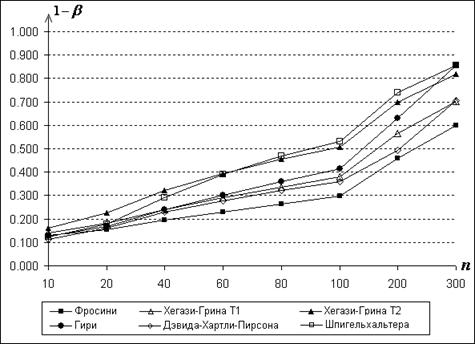
Рис.17. Мощности
критериев по отношению к конкурирующей гипотезе
в зависимости от при
Но при этом необходимо учитывать существенные недостатки критериев Шпигельхалтера и Хегази-Грина:
–
1) критерий Шпигельхалтера
не способен отличить от проверяемой конкурирующие гипотезы типа ;
– 2) критерий Хегази-Грина
со статистикой при малых объемах выборок вследствие смещения также не
способен отличать от проверяемой гипотезы 
конкурирующую гипотезу вида ;
– 3) критерий Хегази-Грина
со статистикой при малых объемах выборок, как и критерии Шапиро-Уилка и Эппса-Палли [2],
так же несколько смещен относительно конкурирующей гипотезы вида .
В приведенном ряду
предпочтительности критерий Эппса-Палли [13],
включенный в стандарт [1], на основании показанной им мощности [2] должен
занять место за критерием Хегази-Грина со статистикой
, а критерий Шапиро-Уилка
[14,15] сразу после критерия Дэвида-Хартли-Пирсона.
В работе [2] мы отдали
предпочтение критерию со статистикой 
[16] , который относительно
рассмотренных конкурирующих гипотез и показал себя наиболее мощным. В приведенном выше ряду предпочтения он просится на
первое место. Однако по отношению к более далекой гипотезе он уступает по мощности
остальным критериям.
Следует отметить, что
относительно наиболее близкой конкурирующей гипотезы критерии согласия 
Андерсона-Дарлинга
и критерий типа Никулина [17,18] в условиях проверки сложной гипотезы
[19,20] лишь не многим уступают по мощности критериям со статистикой , Хегази-Грина,
Шпигельгалтера и Гири, превосходя остальные критерии
проверки отклонения от нормального закона.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 06-01-00059-а).
Литература
1. ГОСТ Р ИСО 5479-2002. Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения. - М.: Изд-во стандартов. 2002. - 30 с.
2. Лемешко Б.Ю., Лемешко С.Б. Сравнительный анализ
критериев проверки отклонения распределения от нормального закона //
Метрология. 2005.
№2. – С.
3-24.
3. Frosini B.V. A survey of a class of goodness-of-fit statistics //Metron. – 1978. V.36. – № 1-2. – P.3-49.
4. Frosini B.V. On the
distribution and power of goodness-of-fit statistic with parametric and
nonparametric applications, “Goodness-of-fit” / Ed. by Revesz
P., Sarkadi K., Sen P.K. –
Amsterdam-Oxford-New York: North Holland Publ.Comp,
1987, P.133-154.
5. Hegazy Y.A.S., Green J.R. Some new goodness-of-fit tests using order statistics //Applied
Statistics. – 1975. – V.24. – №3. – P.299-308.
6. Spiegelhalter D.J. A test for normality against symmetric alternatives //Biometrika. – 1977. – V.64. – №2.
– P.415-418.
7. Geary
R.C. The ratio of the mean deviation to the standard deviation as a test of
normality // Biometrika. – 1935. – V.27. – P.310-322.
8. David
H.A., Hartley H.O., Pearson E.S. The distribution of the
ratio? In a single normal sample, of range to standard deviation // Biometrika. – 1964. – V.512. - №3-4.
– P.484-487.
9. Лемешко Б.Ю., Постовалов С.Н. Компьютерные технологии анализа данных и исследования статистических закономерностей: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2004. – 120 с.
10. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006. – 816 с.
11. Geary R.C.
Moments of the ratio of the mean deviation to the standard deviation for
normal samples // Biometrika. 1936. – V.28. P.295-307.
12. Geary R.C.
Testing for Normality // Biometrika. 1937. – V.34. P.
209-242.
13. Epps T.W., Pulley L.B. A test for normality based
on the empirical characteristic function // Biometrika.
70, 1983. – P. 723-726.
14.
Shapiro S.S., Wilk M.B. An analysis of
variance test for normality (complete samples) // Biometrika,
52, 1965. – P.591-611.
15.
Shapiro S.S., Francia R.S. An approximate analysis of variance test fo normality // J. Amer.
Statist. Assoc., 337, 1972. – P.215-216.
16. D’Agostino
R.B. Transformation to normality of the null distribution of g1 // Biometrika, 57, 1970. – P.679-681.
17. Никулин М.С. О критерии хи-квадрат для непрерывных распределений //Теория вероятностей и ее применение. – 1973. – Т. XVIII. – № 3. – С.675-676.
18. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. – Т. XVIII. – № 3. – С. 583-591.
19. Лемешко Б.Ю., Лемешко С.Б., Постовалов С.Н. Мощность критериев согласия при близких альтернативах // Измерительная техника. 2007. № 2. – С.22-27. [Lemeshko B.Yu., Lemeshko S.B., Postovalov S.N. The power of goodness of fit tests for close alternatives // Measurement Techniques, 2007. V.50, № 2. – P. 132-141]
20. Лемешко Б.Ю., Лемешко С.Б., Постовалов С.Н. Сравнительный анализ мощности критериев согласия при близких конкурирующих гипотезах. II. Проверка сложных гипотез // Сибирский журнал индустриальной математики. 2008. – Т.11. – № 4(36). – С. 78-93.
UDC 519.233.3: 006.91.001
RESEARCH OF FEATURES AND
POWERS OF SOME TESTS OF A REJECTION FROM THE NORMAL LAW
B.Yu. Lemeshko,
A.P. Rogozhnikov
Advantages and
disadvantages are studied, and powers are estimated for different
goodness-of-fit tests for the normal distribution (tests by Frosini,
Hegazy-Green, Spiegelhalter,
Geary and David-Hartley-Pearson).
Key Words: power
of the test; Frosini’s test, Hegazy-Green’s
test, Spiegelhalter’s test, Geary’s test,
David-Hartley-Pearson’s test.