См. также: Прикладная математическая статистика (материалы к семинарам)

ИССЛЕДОВАНИЕ СХОДИМОСТИ РАСПРЕДЕЛЕНИЙ СТАТИСТИК НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СОГЛАСИЯ ПРИ ПРОВЕРКЕ ПРОСТЫХ ГИПОТЕЗ ПО ДИСКРЕТНЫМ ИЛИ ГРУППИРОВАННЫМ ДАННЫМ

С.С. Колесников, Б.Ю. Лемешко

Новосибирский государственный технический университет

Тел. сл. (383) 346-37-54, E-mail: karakazyablek@rambler.ru, headrd@fpm.ami.nstu.ru

Аннотация. Методами статистического моделирования исследуется сходимость к предельным распределений статистик непараметрических критериев согласия Колмогорова и Крамера-Мизеса-Смирнова при использовании преобразования Смирнова для дискретных законов случайных величин и группированных данных.

Постановка задачи

В случае дискретных законов случайных величин или группированных данных при проверке согласия эмпирического распределения с теоретическим законом при проверке простых гипотез не возникает явных проблем только в случае применения критериев согласия типа . Применение же критериев Колмогорова, Крамера-Мизеса-Смирнова или Андерсона-Дарлинга непосредственно невозможно, так как их предельные распределения получены в предположении о непрерывности и случайных величин, и их законов распределения.

Определенный выход видится в использовании преобразования Смирнова [1] и приема, позволяющего перейти от “ступенчатой” и разрывной функции распределения  для дискретных величин и группированных данных к непрерывной.

Например, статистика Колмогорова

с помощью преобразования Смирнова  трансформирует наблюдаемую выборку случайных величин  в выборку величин, равномерно распределенных на интервале [0,1] так, что

,

где эмпирическая функция  строится с использованием .

В данной работе исследуется применение преобразования Смирнова в целях использования непараметрических критериев согласия для проверки простых гипотез о согласии эмпирических распределений с теоретическими для дискретных случайных величин и группированных данных.

Пусть  - функция распределения некоторой дискретной случайной величины. Предположим также что   -  независимых реализаций случайной величины, равномерно распределенной на [0,1]. Тогда случайные величины, полученные рандомизацией в точках разрыва функции

,                                            (1)

где , независимы и равномерно распределены на [0,1].

Соотношение (1) позволяет [1] перейти от дискретной случайной величины к непрерывной, равномерно распределенной на [0,1]. После этого можно проверять простую гипотезу о согласии эмпирического распределения, построенного по , с равномерным законом, используя любой из известных непараметрических критериев согласия.

Преимущества такого подхода очевидны. После преобразования выборки проверяется гипотеза о согласии с непрерывным законом распределения, не требуется модифицировать непараметрические критерии согласия, чтобы учесть дискретность закона распределения или факт группирования данных.

Предполагается, что предельными распределениями статистик применяемых критериев согласия в этом случае являются те же «классические» распределения статистик, и они не зависят от вида закона распределения, которому принадлежит исходная выборка. Вопрос лишь в том, насколько быстро статистика по преобразованным данным сходится к этому предельному распределению? Очевидно лишь, что процедура рандомизации должна отразиться на скорости сходимости.

Целью данной работы является исследование сходимости распределений статистик критериев Колмогорова, Смирнова и Крамера-Мизеса-Смирнова к соответствующим предельным законам при проверке простой гипотезы о согласии с равномерным законом на интервале [0,1] в случае, когда выборка получена с применением преобразования Смирнова и рандомизации некоторой выборки, принадлежащей дискретному закону.

Исследования проводились методами статистического моделирования для 3 дискретных законов распределения: Пуассона, биномиального и дискретного равномерного. Для исследования сходимости распределений статистик к своим предельным законам в зависимости от объема выборок дискретных случайных величин, моделировались выборки объёмом  от 20 до 10000 наблюдений дискретных случайных величин. Объем моделируемых выборок статистик составлял  = 5000 значений.

Результаты исследований

В качестве статистики критерия Колмогорова используется статистика с поправкой Большева

 ,                                                        (2)

где ,  ,   . В случае непрерывных законов случайных величин статистика (2) уже при  хорошо согласуется с предельным распределением Колмогорова .

На рисунке 1 показана сходимость распределения статистики (2) к предельному распределению Колмогорова. Приведены полученные эмпирические распределения  статистики (2) при =20, 50, 1000.

Таблица 1

Распределение	Достигнутый уровень значимости при проверке согласия распределения статистки (2) с
	n=20	n=50	n=100	n=1000	n=10000
Пуассона	0	0	0.0001	0.24	0.83
Биномиальное	0	0	0.03	0.29	0.73
Равномерное	0	0	0.01	0.15	0.15

В таблице 1 приведены достигнутые уровни значимости, полученные при проверке согласия эмпирических распределений статистики (2) с распределением Колмогорова при различных объемах выборок и различных законах дискретных случайных величин: Пуассона, биномиального и дискретного равномерного. 

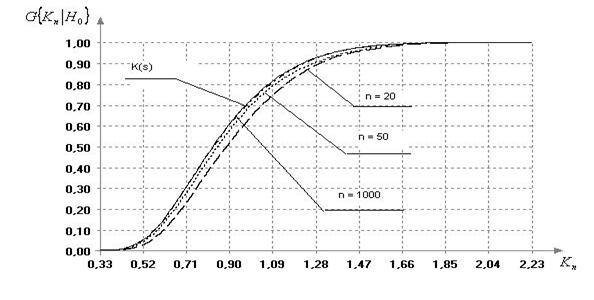
Рис. 1

Аналогичные результаты получены для критерия Смирнова, статистика которого имеет вид

                                                     (3)

При проверке простых гипотез о согласии с непрерывным законом предельным распределением статистики (3) при верной проверяемой гипотезе является -распределение. На рис. 2 показано, как сходится распределение  статистики Смирнова к - распределению при увеличении объёма выборок дискретных случайных величин от 20 до 10000 наблюдений.

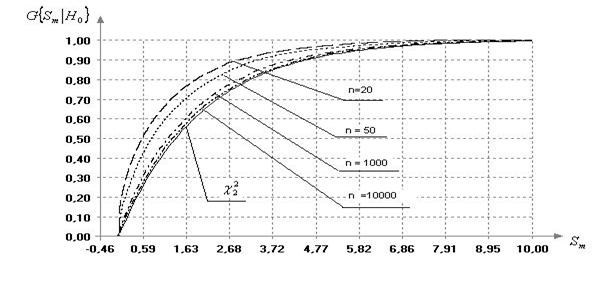
Рис.2

Как видно из рисунка 2, даже при 1000 наблюдениях дискретной случайной величины распределение статистики (3) еще существенно отличается от -распределения, то есть распределение статистики очень медленно сходится к предельному. Следует отметить, что если в случае критерия Колмогорова использование предельного распределения  при ограниченных объемах выборок приводит к увеличению ошибки 1-го рода, то в данном случае опора на -распределение увеличивает вероятность ошибки второго рода.

Отметим, что согласие распределения статистики (3) с -распределением достигается для биномиального и дискретного равномерного распределений только при =10000. Для пуассоновского распределения даже в этом случае гипотезу о согласии следует отклонить.

 Статистика  критерия Крамера-Мизеса-Смирнова имеет вид

                                         (4)

и в пределе при верной проверяемой гипотезе подчиняется распределению . Сходимость распределения  статистики (4) к предельному при дискретных случайных величинах в зависимости от объёма выборки иллюстрирует рис. 3. Проверка согласия полученных эмпирических распределений статистики (4) с распределением  при различных объемах выборок и законах дискретных величин показала, что распределение статистики (4) сходится к предельному не хуже статистики Колмогорова.

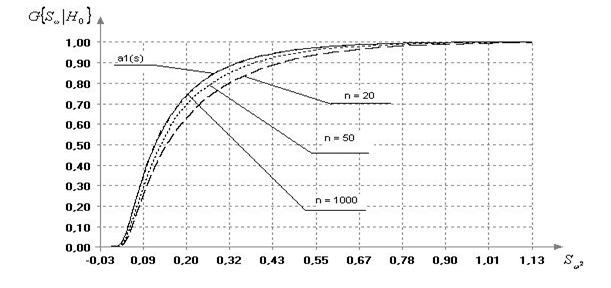
Рис. 3

Заключение

Результаты исследований позволяют сделать вывод о хорошей возможности применения рассмотренного подхода к проверке согласия с дискретными или группированными данными. Распределения статистик Колмогорова и Крамера-Мизеса-Смирнова достаточно быстро сходятся к своим предельным распределениям при объемах выборок в несколько сотен наблюдений. Сходимость к предельному распределения статистики Смирнова существенно ниже. При малых объемах выборок следует учитывать отклонения распределений статистик от предельного.

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а).

Литература

1. Greenwood P.E., Nikulin M.S. A Guide to Chi-Squared Testing. – John Wiley & Sons, Inc. 1996. – 280 p.