См. также: Прикладная математическая статистика (материалы к семинарам)

 

Метрология. 2004. №4.– С.3-15

 

519.233.3: 006.91.001

Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального

Б.Ю. Лемешко, С.С. Помадин

 

Методами статистического моделирования исследованы распре­деле­ния классических статистик, используемых при проверке гипотез о мате­матических ожиданиях и дисперсиях. Показано, что при проверке гипотез о математических ожиданиях применение классических результатов ока­зывается корректным при существенных отклонениях наблюдаемого за­кона от нормального. Для статистик, используемых в критериях проверки гипотез о дисперсиях, получены таблицы процентных точек, применение которых правомерно при наблюдаемых законах, описываемых экспонен­циальным семейством распределений.

 

The classical statistic distributions used in testing hypotheses on mathe­matical expectations and variances have been investigated by means of statisti­cal modeling methods. It has been shown that in testing hypothesis about mathematical expectations the usage of classical results turns out to be correct even when an observed law essentially differs from the normal distribution. The tables of percentage points, which can be used for correct testing hypotheses about variances when observed laws are described with the exponential distri­bution family, have been obtained.

 

Введение

При поверке измерительных приборов, в задачах контроля качества и в других приложениях возникает необходимость в проверке статисти­ческих гипотез о значении математического ожидания  или о значении дисперсии . В основе применяемого классического аппарата проверки гипотез такого вида лежит предположение о принад­лежности наблюдаемых данных (ошибок измерений) нормальному за­кону распределения. В то же время, не секрет, что ошибки измеритель­ных приборов и систем во многих случаях не удается удовлетворительно описать моделью нормального закона [1]. Однако и в этом случае сохра­няется актуальность решения задач проверки гипотез о математических ожиданиях и дисперсиях наблюдаемого закона. Насколько корректно в этом случае применение классического аппарата проверки данных гипо­тез? Когда можно без боязни использовать классические критерии, а ко­гда их применение является некорректным? И как следует поступать в последнем случае?

В литературных источниках можно найти аналитические оценки, характеризующие устойчивость критериев проверки гипотез о математи­ческих ожиданиях по отношению к виду наблюдаемого закона, и указа­ния на существенную зависимость от вида закона критериев проверки гипотез о дисперсиях. Сведения, которые практик может почерпнуть из этого, сводятся к тому, что при нарушении нормальности нельзя исполь­зовать классические результаты для проверки гипотез о дисперсиях, а для проверки гипотез о математических ожиданиях, по-видимому, можно, но с долей осторожности.

Целью данной работы явилось желание исследовать, что происхо­дит с распределениями классических статистик, используемых в крите­риях проверки гипотез о математических ожиданиях и дисперсиях, если наблюдаемый закон в той или иной мере отличается от нормального; проверить, насколько будут корректны статистические выводы, бази­рующиеся на классических результатах, если нарушено предположение о нормальности; дать в руки исследователя необходимый математический аппарат, обеспечивающий корректность выводов при законах распреде­ления, существенно отличающихся от нормального. Результаты, пред­ставленные в данной работе, получены с использованием развиваемой и хорошо зарекомендовавшей себя методики статистического моделирова­ния и компьютерного анализа [2], позволяющей с меньшими трудно­стями получать фундаментальные знания о статистических закономерно­стях.

Классические критерии проверки гипотез о математических ожи­даниях и дисперсиях. Пусть мы имеем выборку  случайных величин, рас­пределенных по нормальному закону . В этом слу­чае задачи проверки гипотез о математических ожиданиях и дисперсиях формулируются следующим образом.

1. В критерии проверки гипотез вида  при известной диспер­сии  используется статистика , которая при справедли­вости гипотезы  подчиняется нормальному распределению: 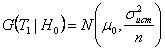. Проверяемая гипотеза  отклоняется при боль­ших отклонениях  от .

2. Для проверки гипотезы  при неизвестной дисперсии  используется статистика , где , . При справедливости  статистика  распределена как  – распределение Стьюдента.

3. Для проверки гипотезы вида  при известном математиче­ском ожидании  вычисляется статистика , условным распределением которой является  – распределение.

4. В критерии проверки гипотезы вида  при неизвестном математическом ожидании  используется статистика , подчиняющаяся  – распределению.

Для иллюстрации работоспособности применяемой методики ис­следований приведем результаты моделирования эмпирических распре­делений данных статистик в случае нормального закона регистрируемых наблюдений. В дальнейшем N указывает на объемы смоделированных выборок статистик рассматриваемых критериев.

В качестве примера рассмотрены распределения статистик , , ,  при проверяемых гипотезах  и . На рис. 1 отражены по­лученные в результате моделирования эмпирические распределения статистик ,  и теоретические распределения данных статистик при нормальности наблюдаемого закона. Видно, что смоделированные рас­пределения статистик, используемых при проверке гипотез о значении математического ожидания, визуально совпадают со своими предель­ными законами: нормальным и  – распределением Стьюдента. Количе­ственной мерой близости полученных эмпирических распределе­ний статистик и теоретических предельных служат достигнутые уровни значимости  по критериям согласия  Пирсона, Колмогорова,  Крамера-Мизеса-Смирнова,  Андерсона-Дарлинга [3,4], где S – ста­тистика соответствующего критерия согласия, – ее значение, вычислен­ное по конкретной выборке исследуемых статистик , , , . Чем больше достигнутый уровень значимости, чем ближе он к 1, тем лучше согласуется эмпирическое распределение статистики с теоретиче­ским. Приведенные в таблице 1 значения достигнутых уровней значимости  для статистик   и  говорят об очень высо­кой близости полученных в результате моделирования эмпириче­ских распределений статистик к предельным. Аналогичная картина на­блюдается на рис. 2 и табл. 2, где приведены результаты моделирования распределений статистик , , используемых в критериях проверки гипо­тез о значениях дисперсии.

Таблица 1. Значения достигнутых уровней значимости критериев согласия для примера на рис. 1







 

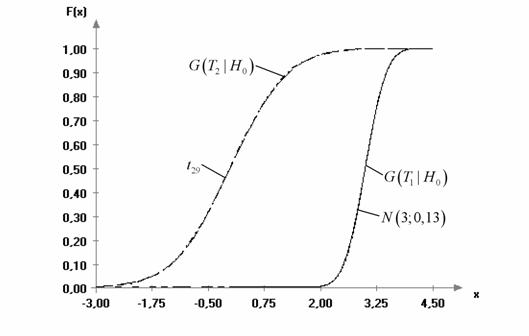
Рис. 1. Эмпирические и теоретические функции распределения статистик ,  при проверке гипотезы  при известной () и неизвест­ной дисперсии: n = 30; N = 10000

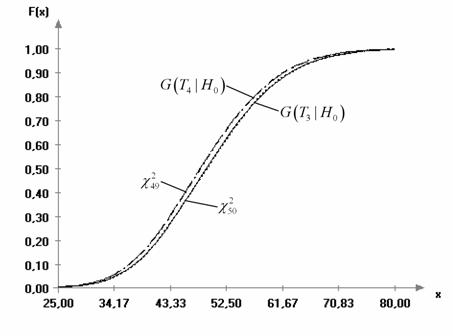
Рис. 2. Эмпирические и теоретические функции распределения статистик  и  при проверке гипотезы  при известном () и неиз­вестном математическом ожидании (n = 50 и N = 10000)

Таблица 2. Значения достигнутых уровней значимости критериев согласия для примера на рис. 2







 

Распределения статистик , , ,  при нарушении предположе­ний о нормальности. В работе [5] мы исследовали распределения стати­стик ,  в случае принадлежности наблюдаемых случайных величин распределениям экстремальных значений, логистическому и Лапласа. В данном случае рассмотрено распределение, более перспективное для описания ошибок измерений. Очень хорошей моделью для закона рас­пределения ошибок конкретной измерительной системы иногда оказыва­ется одно из распределений экспоненциального семейства с плотностью

,

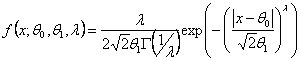где  – параметр сдвига,  – параметр масштаба, l – параметр формы. Ча­стными случаями данного семейства распределений являются нор­мальный закон при l = 2 и распределение Лапласа при l = 1. Предель­ными слу­чаями – распределение Коши () и равномерное распределе­ние ().

Далее будем рассматривать распределения статистик , , ,  в случае принадлежности наблюдаемых случайных величин экспоненци­альному семейству распределений , . Предельные распределения статистик , , ,  известны только для частного слу­чая при l = 2 (для нормального закона).

Для статистик, вычисляемых по выборкам случайных величин , , распределенных по экспоненциальному семей­ству с параметром формы l, введем обозначения .

Результаты моделирования выборок статистик  и  в случае при­надлежности на­блюдаемых величин экспоненци­альному семейству рас­пределений (параметр l изменялся в диапа­зоне от 1 до 10) показали, что значимого изменения предельных распределений статистик  и , ис­поль­зуемых в критериях проверки гипотез о значениях математиче­ского ожидания (при известной и неизвестной дисперсии), не происходит.

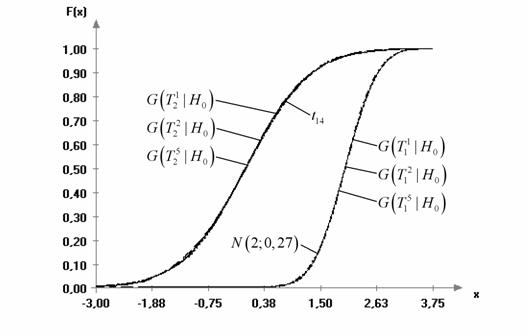
Рис. 3. Эмпирические и теоретические функции распределения статистик  и  при проверке гипотезы  при известной () и неизвест­ной дисперсии: n = 15; N = 5000

На рис. 3 в качестве примера представлены графики теоретических пре­дельных, соответствующих классиче­скому случаю, и полученных эмпи­рических функций распределения статистик  и , используемых при проверке гипо­тезы  при известной () и неизвестной диспер­сиях. Визуальная близость распределений статистик, построенных в случае принадлежности выборок экспоненциальному се­мейству, к пре­дельным (классическим) распределениям, полученным для нормального закона, позво­ляет отметить, что значимого изменения распределений статистик не произошло. Это же подтверждает применение критериев согласия для проверки значимости отклонений смоделированных эмпи­рических распределений статистик  и  от классических предельных распределений (при нормальном законе наблюдаемых величин). Достиг­нутые уровни значимости  представлены в таблице 3.

Таблица 3. Значения достигнутых уровней значимости критериев согласия для примера на рис. 3



















 

Результаты исследований рас­пределений статистик  и  позво­ляют утверждать, что в случае отклонений наблюдаемого за­кона от нор­мального (при сохранении симметричности), использование классиче­ских предельных рас­пределений для статистик  и  не нарушает кор­ректности выводов статистического ана­лиза при проверке гипотез вида .

В случае несимметричных законов наблюдаемых величин, напри­мер, при распределениях экстремальных значений, распределения стати­стик  и  претерпевают значимые изменения, которые можно заметить как визуально, так и с использованием критериев согласия. Соответст­вующий пример демонстрирует картина, представленная на рис. 4. При­мер свидетельствует все-таки об ограниченной области устойчивости критериев проверки гипотез о математическом ожидании. В таблице 4 приведены достигнутые значения уровня значимости, которые свидетельствуют, что, не смотря на визуальную близость эмпирического распределения статистики к теоретическому, в данном случае гипотеза о нормальности статистики  при уровне значимости  должна быть отклонена

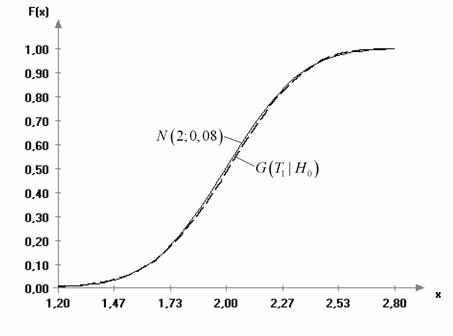
Рис. 4.  Эмпирическая и теоретическая функции распределения стати­стики , смоделированной по распределению минимального значения, при проверке гипотезы  для известной дисперсии ():  n = 50;  N = 5000

Таблица 4. Значения достигнутых уровней значимости критериев согласия для примера на рис. 4




 

В отличие от  и  распределения статистик  и , используемых в критериях проверки гипотез о диспер­сии, как в случае известного ма­тематического ожидания, так и в случае неизвестного очень чувст­ви­тельны к виду наблюдаемого закона распределения. Иллюстрацией к сказанному являются рисунки 5 и 6, на которых изображены графики эмпирических функций распре­делений статистик  и , смоделирован­ных при экспоненциальном семействе с параметром формы l равным 1 и 10. На рисунках приведены также предельные рас­пределения статистик  и  в случае нормального закона (и  –рас­пределения, соответственно).

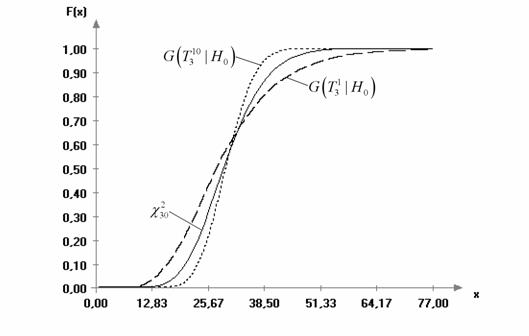
Рис. 5. Теоретическая и эмпирические функции распределения статистики  при проверке гипотезы  при известном () математическом ожидании: n = 30; N = 5000

Из представленной на рис. 5 картины очевидно, что распределения статистики , смоделированные при выборках случайных ве­личин, при­надлежащих экспоненциальному семейству с параметром формы не рав­ным 2, существенно отличаются от предельного распределения, полу­ченного для нормального закона. Аналогичную зависимость от вида на­блюдаемого закона демонстрирует статистика  при проверке гипотезы о значении дисперсии при неизвестном математическом ожидании (см. рис. 6).

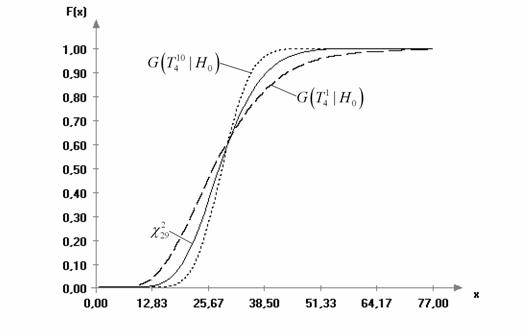
Рис. 6. Теоретическая и эмпирические функции распределения статистики  при проверке гипотезы  при неизвестном математическом ожидании: n = 30; N = 5000

Результаты проведенных исследований говорят о том, что распреде­ления статистик, используемых при проверке гипотез о дисперсии (ма­тематическое ожидание известно или неизвестно), значимо отличаются от клас­сических предельных при отклонениях наблюдаемого закона от нормального. Поэтому при использовании классических процедур для проверки гипотез о дис­персии целесообразно удостовериться в том, что наблюдаемый закон является нормальным, применяя соответствующие критерии проверки нормальности.

Таким образом, приводимые результаты показывают, с одной сто­роны, высокую устойчивость к отклонениям от нормальности наблюдае­мых величин критериев проверки гипотез о математических ожиданиях. А, с другой стороны, – неустойчивость критериев, используемых при проверке гипотез о дисперсиях. В то же время результаты подтверждают надежность развиваемой методики исследований и возможность по­строения моделей предельных распределений для статистик  и  при произвольных наблюдаемых законах случайных величин, что актуально для различных приложений задач статистического анализа данных.

Для построения приближенных моделей, наилучшим образом опи­сывающих распределения статистик  и  при конкретных значениях l и n, принципиальных трудностей нет. К сожалению, не удается по­строить аналитические модели распределений данных статистик с пара­метрами, зависящими от l и n. Поэтому на основании результатов стати­стического моделирования были вычислены таблицы верхних процент­ных точек (квантилей) для ряда значений l и n. Процентные точки рассчитывались по выборкам значений статистик достаточно больших объемов (N = 100000, N = 150000 и N = 200000), а затем усреднялись по ряду экс­периментов.

Полученные процентные точки для статистик  и  при пара­метре формы экспоненциального семейства, равном 1; 1,5; 3; 4; 5 и 10, представлены в таблицах 5 и 6 соответственно. Значения процентных точек при параметре формы l = 2,  приведенные в таблицах, соответствуют предельным распределениям статистик при нормальном законе наблю­даемых величин.

Таблица 5. Верхние процентные точки для статистики  в случае принадлежности наблюдаемого закона экспоненциальному семейству с параметром формы l

 

 

l = 1

l = 1,5

l = 2

l = 3

l = 4

l = 5

l = 10

n = 15

a = 0,15

22,94

21,45

20,64

19,76

19,39

19,18

18,81

a = 0,1

25,98

23,54

22,34

21,06

20,58

20,28

19,77

a = 0,05

31,38

26,98

25,01

23,08

22,41

21,96

21,22

a = 0,025

37,02

30,23

27,46

24,88

24,04

23,45

22,51

a = 0,01

44,36

34,40

30,59

27,03

26,00

25,21

24,02

n = 30

a = 0,15

41,85

39,31

38,01

36,79

36,21

35,89

35,37

a = 0,1

45,97

42,09

40,26

38,60

37,84

37,41

36,71

a = 0,05

52,92

46,49

43,80

41,37

40,28

39,70

38,70

a = 0,025

59,56

50,59

46,97

43,80

42,47

41,72

40,46

a = 0,01

68,51

55,65

50,88

46,78

45,08

44,15

42,52

n = 50

a = 0,15

65,86

62,02

60,30

58,77

58,02

57,60

56,91

a = 0,1

70,83

65,50

63,15

61,00

60,04

59,51

58,61

a = 0,05

78,47

70,91

67,51

64,42

63,10

62,36

61,17

a = 0,025

85,83

75,66

71,34

67,51

65,86

64,94

63,39

a = 0,01

95,36

81,92

76,15

71,24

69,22

67,98

66,05

n = 100

a = 0,15

122,67

116,99

114,57

112,34

111,27

110,69

109,77

a = 0,1

129,31

121,54

118,47

115,47

114,13

113,38

112,15

a = 0,05

139,98

128,64

124,29

120,07

118,37

117,38

115,67

a = 0,025

149,80

135,17

129,33

124,27

122,14

120,90

118,78

a = 0,01

162,04

143,38

135,95

129,27

126,64

125,05

122,42

Таблица 6. Верхние процентные точки для статистики  в случае принадлежности наблюдаемого закона экспоненциальному семейству с параметром формы l

 

 

l = 1

l = 1,5

l = 2

l = 3

l = 4

l = 5

l = 10

n = 15

a = 0,15

21,49

20,16

19,40

18,65

18,34

18,14

17,82

a = 0,1

24,38

22,19

21,03

19,95

19,53

19,26

18,80

a = 0,05

29,52

25,46

23,65

21,92

21,34

20,94

20,27

a = 0,025

34,79

28,64

26,12

23,71

22,95

22,41

21,56

a = 0,01

41,88

32,70

29,25

25,85

24,94

24,22

23,09

n = 30

a = 0,15

40,54

38,09

36,88

35,71

35,17

34,89

34,39

a = 0,1

44,53

40,83

39,11

37,49

36,79

36,42

35,73

a = 0,05

51,36

45,20

42,60

40,25

39,25

38,71

37,73

a = 0,025

57,85

49,20

45,74

42,70

41,41

40,77

39,51

a = 0,01

66,49

54,21

49,59

45,61

44,01

43,13

41,60

n = 50

a = 0,15

64,62

60,90

59,24

57,70

56,99

56,59

55,92

a = 0,1

69,58

64,30

62,06

59,95

59,01

58,51

57,63

a = 0,05

77,18

69,65

66,39

63,35

62,07

61,37

60,17

a = 0,025

84,42

74,42

70,20

66,46

64,79

63,96

62,41

a = 0,01

93,75

80,63

74,94

70,21

68,13

66,98

65,05

n = 100

a = 0,15

121,51

115,87

113,54

111,29

110,26

109,71

108,77

a = 0,1

128,08

120,45

117,35

114,43

113,11

112,39

111,15

a = 0,05

138,70

127,50

123,22

119,07

117,36

116,38

114,67

a = 0,025

148,27

134,04

128,29

123,18

121,07

119,87

117,79

a = 0,01

160,22

142,27

134,71

128,13

125,55

124,04

121,34

Выводы

Таким образом, численные исследования подтвердили устойчивость распределений статистик  и , используемых в критериях проверки ги­потез о математических ожиданиях, к отклонениям наблюдаемого за­кона от нормального. Эмпирические распределения статистик  и  хо­рошо согласуются с предельными, полученными в предположении о нормальности наблюдаемого закона. Это позволяет на практике кор­ректно применять классические результаты при наблюдаемых законах, существенно отличающихся от нормального. В частности, в таких ситуациях можно уверенно руководствоваться стандартом [6].

Полученные здесь результаты подчеркивают общую закономер­ность: критерии, связанные с проверкой гипотез о математических ожи­даниях устойчивы к отклонениям наблюдаемых величин от нормального закона. Это было показано ранее при исследовании распределений ста­тистик, используемых при проверке гипотез о векторе математических ожиданий и коэффициентах корреляции многомерных законов распре­делений [7].

В то же время, распределения статистик  и  очень существенно за­висят от вида наблюдаемого закона. Если наблюдаемый закон значимо отличается от нормального, использование классических результатов для данных критериев недопустимо, так как такая попытка неизбежно при­ведет к некорректным выводам. В тех ситуациях, когда хорошей моде­лью для наблюдаемых случайных величин оказывается экспоненциаль­ное семейство распределений с параметром  формы l, можно воспользо­ваться таблицами процентных точек, полученными в данной работе.

Работа выполнена при финансовой поддержке Минобразования РФ (проекты № Т02-3.3-3356 и № А03-2.8-280)

 

Литература

1.      Новицкий П.В., Зограф И.А. Оценка погрешностей результатов из­ме­рений. – Л.: Энергоатомиздат, 1991. – 303 с.

2.      Лемешко Б.Ю. Компьютерные методы исследований статистических закономерностей // Сб. "Моделирование, автоматизация и оптимиза­ция наукоемких технологий". - Новосибирск: изд-во НГТУ, 2000. - С. 18-19.

3.      Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.

4.      Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть II. Непараметрические критерии. – М.: Изд-во стандар­тов. 2002. – 64 с.

5.      Лемешко Б.Ю., Ванюкевич О.Н. Проверка гипотез о дисперсии при на­рушении предположений о нормальности // Сб. научных трудов НГТУ. – 2002. – № 3(29). – С.27-32.

6.      ГОСТ Р 50779.53-98. Приемочный контроль качества по количес­т­венному признаку для нормального распределения. Часть 1. Стан­дартное отклонение известно. – М.: Изд-во стандартов. 1998. – 23 с.

7.      Лемешко Б.Ю., Помадин С.С. Корреляционный анализ наблюдений многомерных случайных величин при нарушении предположений о нормальности // Сибирский журнал индустриальной математики. 2002. – Т.5. – № 3. – С.115-130.