См. также: Прикладная математическая статистика (материалы к семинарам)

Измерительная техника. 2005.  № 12. – С.9-14

УДК 519.24

О СХОДИМОСТИ РАСПРЕДЕЛЕНИЙ СТАТИСТИК И МОЩНОСТИ КРИТЕРИЕВ ОДНОРОДНОСТИ СМИРНОВА И ЛЕМАНА-РОЗЕНБЛАТТА

Лемешко Б.Ю., Лемешко С.Б.

Исследуются распределения статистик критериев проверки однородности Смирнова и Лемана-Розенблатта при ограниченных объемах выборок и их сходимость к предельным. Рассматриваются особенности применения критерия Смирнова. Предлагается поправка, обеспечивающая большую близость распределения статистки критерия Смирнова к предельному распределению Колмогорова. Сравнивается мощность критериев по отношению к различным альтернативам. Даются рекомендации по применению.

Ключевые слова: критерий однородности Смирнова, критерий однородности Лемана-Розенблатта, мощность критерия.

Statistical distribution convergence and homogeneity test power for Smirnov and Lehmann–Rosenblatt tests

Lemeshko B.Yu., Lemeshko S.B.

The distributions of Smirnov and Lehmann-Rosenblatt homogeneity test statistics have been investigated for the limited sample sizes. The convergence of the statistic distributions to the corresponding limiting laws has been investigated. The features of using Smirnov test have been considered. The correction providing the closeness of Smirnov test statistic distribution to the limiting Kolmogorov law has been suggested. These tests have been compared by the power with respect to different alternatives. The recommendations on the usage have been given.

Key words: Smirnov homogeneity test, Lehmann-Rosenblatt homogeneity test, test power.

Введение. Любой статистически критерий проверки гипотез представляет собой средство измерения. Поэтому пользоваться им следует также квалифицированно, как и любым техническим измерительным средством. По крайней мере, следует понимать, что он измеряет, особенности применения, к каким результатам можно прийти, с какими ошибками это связано.

С необходимостью решения задач проверки гипотез о принадлежности двух выборок случайных величин одной и той же генеральной совокупности постоянно сталкиваются при анализе случайных ошибок средств измерений, при статистическом управлении качеством процессов. Такая задача естественно возникает при поверке средств измерений, когда пытаются убедиться в том, что закон распределения случайных ошибок измерений не претерпел существенных изменений по истечении некоторого интервала времени.

Среди множества статистических критериев, параметрических и непараметрических, используемых для проверки однородности, выделяют три группы критериев: для проверки гипотез о средних (о математических ожиданиях и медианах), для проверки гипотез о характеристиках рассеяния (о дисперсиях и размахах), для проверки гипотез о законах распределения.

У исследователя, стоящего перед проблемой решения таких задач, не смотря на обилие публикаций, возникает множество вопросов, так как остается неясным, в каких случаях применение какого критерия оказывается более предпочтительным.

Такие вопросы возникают относительно критериев проверки гипотез о средних, где мы имеем множество критериев (параметрических и непараметрических), но не имеем четких указаний и сведений о преимуществе тех или иных. Например, о степени их устойчивости к отклонениям от стандартных предположений, о результатах сравнения мощности критериев. Отсутствие указаний не позволяет в конкретной ситуации выбрать наиболее мощный критерий. По поводу некоторых критериев проверки гипотез о средних имеется информация об относительной устойчивости распределений статистик к отклонениям наблюдаемого закона от нормального [1,2]. По отношению к другим критериям это требует дополнительных исследований.

Критерии проверки гипотез о дисперсиях наоборот весьма чувствительны к любым отклонениям от предположений, в условиях которых они были получены. И также отсутствует или противоречива информация относительно мощности соответствующих критериев [3,4].

Неотклонение проверяемых гипотез о равенстве средних и (или) равенстве дисперсий еще не говорит о принадлежности выборок одной и  той же генеральной совокупности. Это говорит лишь о возможном равенстве числовых характеристик, но не законов распределения. Выбор же критериев проверки гипотез относительно законов распределения, соответствующих двум выборкам, более скромен. Как правило, на практике используется либо критерий Смирнова, либо критерий Лемана-Розенблатта [3]. Предпочтительность использования данных критериев для проверки однородности обсуждалась в [5].

Цель настоящей работы состояла в исследовании распределений статистик и мощности критериев Смирнова и Лемана-Розенблатта при ограниченных объемах выборок, в уточнении объемов, начиная с которых можно реально пользоваться предельными распределениями, в выяснении характера альтернатив, относительно которых тот или иной критерий имеет преимущество в мощности. При проведении исследований использовалась методика компьютерного моделирования и анализа статистических закономерностей, хорошо зарекомендовавшая себя в предыдущих работах (например, [1,4]), базирующаяся в основном на методе статистического моделирования.

Задача проверки однородности двух выборок формулируется следующим образом. Пусть имеется две упорядоченные по возрастанию выборки размера  и :

  и  .

Для определенности обычно полагают, что . Проверяется гипотеза о том, что две выборки извлечены из одной и той же генеральной совокупности, т.е. :  при любом .

Критерий Смирнова. Критерий однородности Смирнова предложен в работе [6]. Предполагается, что функции распределения  и  являются непрерывными. Статистика критерия Смирнова измеряет различие между эмпирическими функциями распределения, построенными по выборкам

.

При практическом использовании критерия значение статистики  рекомендуется вычислять в соответствии с соотношениями [3]

,

,

.

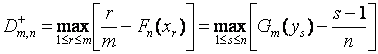Если гипотеза  справедлива, то при неограниченном увеличении объемов выборок [3] 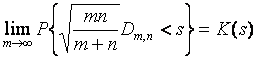, т.е. статистика

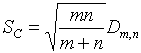                                                          (1)

в пределе подчиняется распределению Колмогорова  [3]. Однако при ограниченных значениях  и  случайные величины  и  являются дискретными, и множество их возможных значений представляет собой решетку с шагом , где  наименьшее общее кратное  и  [3]. Для значений  таблицы процентных точек для статистики  приводятся в [3]. Условное распределение  статистики  при справедливости гипотезы  медленно сходится к  и существенно отличается от него при не очень больших  и . Асимптотические формулы для распределений  и  рассматривались в [7, 8, 9].

На рис. 1 показаны условные распределения статистики (1) при справедливости  в зависимости от  и  (при =). Как следует из полученной картины, даже при  и  ступенчатость  сохраняется. Другим недостатком применения критерия со статистикой (1) является то (см. рис. 1), что распределения  с ростом  и  приближаются к предельному распределению  слева.

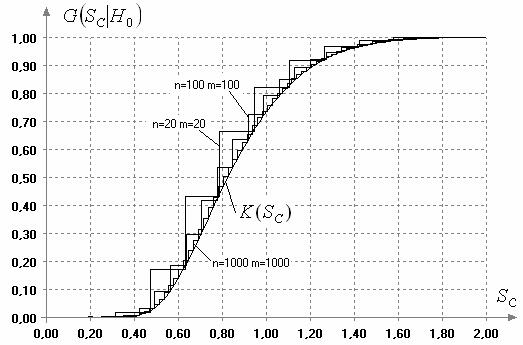
Рис. 1. Распределения статистики (1) при справедливости  в зависимости от  и

Гладкость распределения статистики сильно зависит от величины . Поэтому предпочтительнее применять критерий, когда объемы выборок  и  не равны и представляют собой взаимно простые числа. В таких случаях наименьшее общее кратное  и  максимально и равно , а распределение статистики существенно больше напоминает непрерывную функцию распределения. И вот тогда при небольших и умеренных значениях  и  проявляется существенное отличие распределения от предельного , так как  заметно сдвинуто влево от .

В этой связи можно предложить следующую простую модификацию статистики (1), 

,                                           (2)

у которой практически отсутствует последний недостаток. Условные распределения статистики (2) при справедливости  в зависимости от  и  (при =) иллюстрирует рис. 2.

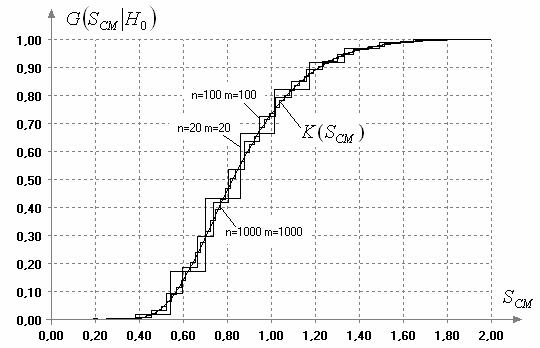
Рис. 2. Распределения статистики (2) при справедливости  в зависимости от  и

Как было сказано выше, гладкость распределения статистики зависит от величины . В качестве иллюстрации этого факта и различий в распределениях статистик (1) и (2) на рис. 3 приведены предельное распределение Колмогорова  и полученные в результате моделирования эмпирические распределения  статистики (1) и  статистики (2) при  и . Как видим, распределение статистики (1) существенно отличается от распределения Колмогорова , а распределение статистики (2) визуально практически совпадает с ним. Объем выборок смоделированных значений статистик в данном случае, как и во всех остальных в данной работе, составил 10000 наблюдений. При проверке согласия полученного эмпирического распределения статистики (2) с распределением Колмогорова достигнутые уровни значимости по соответствующим критериям составили: 0.72 по критерию  Пирсона (при 10 равновероятных интервалах), 0.83 по критерию Колмогорова, 0.97 по критерию Крамера-Мизеса-Смирнова, 0.94 по критерию Андерсона-Дарлинга.

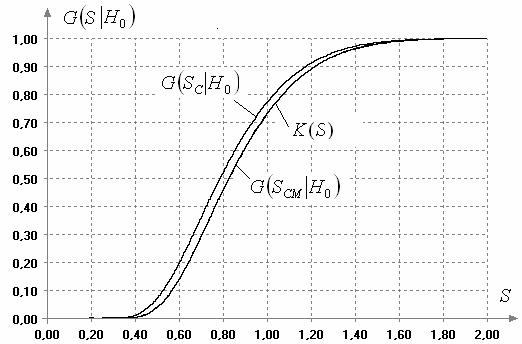
Рис. 3. Распределения статистики (1) и (2) при справедливости ,  и

Использование в критерии Смирнова со статистикой (2) взаимно простых  и  делает более обоснованным вычисление достигаемого уровня значимости , где  – значение статистики (2), найденное при проверке гипотезы  по конкретным выборкам, в соответствии с распределением Колмогорова: . Соответственно, более правомерно применение в критерии процентных точек (квантилей) распределения Колмогорова. Этого нельзя сказать относительно критерия Смирнова со статистикой (1), так как в этом случае критические значения, определяемые по распределению Колмогорова, оказываются завышенными по сравнению с истинными. Следовательно, проверяемая гипотеза может необоснованно приниматься (не отклоняться).

Коэффициент 4.6 в статистике (2) подобран эмпирически. Он удовлетворительно действует от малых до очень приличных объемов выборок (==1000). Однако при больших значениях наименьшего общего кратного  и , когда они представляют собой взаимно простые числа, величина этого коэффициента должна быть несколько уменьшена. Например, при простых  и  коэффициент 4.6 следует заменить на 3.4.

Ниже при исследовании мощности критерия Смирнова рассматривались распределения статистики (1). Но все выводы относительно мощности справедливы и для критерия со статистикой (2), так как все распределения при одинаковых объемах выборок оказываются сдвинутыми на одну и ту же величину [см. (2)].

Предвосхищая вопросы о точности, отметим, что для проверки соответствия результатов моделирования имеющимся теоретическим [3] нами специально моделировались распределения статистики . Результаты показали полное совпадение критических значений, получаемых в процессе моделирования, с точными критическими значениями статистики, приводимыми в [3].

В данной работе мощность критериев проверки однородности исследовалась при ряде альтернатив. Для определенности гипотезе  соответствовала принадлежность выборок одному и тому же стандартному нормальному закону распределения с плотностью

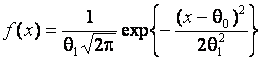
с параметрами сдвига  и масштаба . При всех альтернативах первая выборка всегда соответствовала стандартному нормальному закону, а вторая – некоторому другому. В частности, в случае гипотезы  вторая выборка соответствовала нормальному закону с параметром сдвига  и параметром масштаба . В случае гипотезы  – нормальному закону с параметрами  и . В случае гипотезы  – нормальному закону с параметрами  и . В случае гипотезы  – нормальному закону с параметрами  и . В случае гипотезы  – вторая выборка соответствовала логистическому закону с плотностью

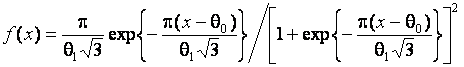
и параметрами  и . Нормальный и логистический законы очень близки и трудно различимы с помощью критериев согласия. На рис. 4 представлены полученные в результате моделирования условные распределения статистики  при справедливости , на основании которых можно оценить значения мощности при различных значениях объемов выборок  и .

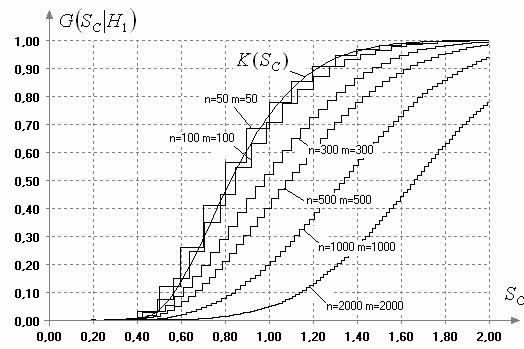
Рис. 4. Распределения статистики (1) при справедливости

Аналогичным образом при различных объемах выборок были построены условные распределения статистики (1) при справедливости других рассматриваемых альтернатив: , , , .  На основании этих распределений и предельного распределения статистики = были вычислены значения мощности критерия относительно различных альтернатив. Найденные значения мощности  критерия Смирнова, где  - вероятность ошибки второго рода, относительно рассматриваемых конкурирующих гипотез  ÷  при различных объемах выборок для уровней значимости (вероятностей ошибок первого рода) =0.1, 0.05, 0.025 представлены в таблице 1.

Таблица 1. Мощность критерия однородности Смирнова относительно альтернатив ÷ в зависимости от объемов выборок ()

Уровень значимости	Значения мощности относительно альтернативы
	n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,0937	0,1480	0,1766	0,2775	0,3806	0,6171	0,8688
0,05	0,0410	0,0569	0,0944	0,1883	0,2682	0,4899	0,7762
0,025	0,0410	0,0344	0,0505	0,1163	0,1829	0,3859	0,6737
	Значения мощности относительно альтернативы
0,1	0,3457	0,7200	0,9332	1	1	1	1
0,05	0,2202	0,5341	0,8722	0,9996	1	1	1
0,025	0,2202	0,4328	0,7842	0,9992	1	1	1
	Значения мощности относительно альтернативы
0,1	0,0884	0,1229	0,1257	0,1466	0,1856	0,2967	0,5508
0,05	0,0352	0,0458	0,0630	0,0789	0,1024	0,1677	0,3520
0,025	0,0352	0,0257	0,0280	0,0410	0,0518	0,0967	0,2098
	Значения мощности относительно альтернативы
0,1	0,1396	0,2986	0,5213	0,9609	0,9989	1	1
0,05	0,0570	0,1268	0,3161	0,8977	0,9952	1	1
0,025	0,0570	0,0763	0,1689	0,7738	0,9786	1	1
	Значения мощности относительно альтернативы
0,1	0,0836	0,1209	0,1308	0,1568	0,1976	0,3191	0,5639
0,05	0,0341	0,0455	0,0673	0,0891	0,1158	0,1879	0,3754
0,025	0,0341	0,0258	0,0316	0,0471	0,0618	0,1119	0,2390

Подчеркнем, что значения мощностей, приведенные в таблице 1, получены относительно ()-квантилей предельного распределения Колмогорова . Вследствие того, что распределения  статистики (1) существенно отличаются от , действительные уровни значимости отличаются от заданных =0.1, 0.05, 0.025. В таблице 2 приведены действительные уровни значимости для критерия Смирнова, соответствующие значениям мощности, представленным в таблице 1. Вследствие ступенчатости  действительные значения  особенно сильно отличаются от задаваемых при малых объемах выборок. Например, для при задаваемом уровне значимости 0.1 мы имеем действительный уровень значимости 0.0835.

Таблица 2. Действительные уровни значимости критерия однородности Смирнова, соответствующие (1-)–квантилям распределения Колмогорова, в зависимости от объемов выборок ()

Заданный уровень значимости	Действительные уровни значимости
	n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,0835	0,1120	0,1085	0,0927	0,0970	0,0980	0,1041
0,05	0,0334	0,0410	0,0543	0,0496	0,0514	0,0471	0,0480
0,025	0,0334	0,0240	0,0252	0,0254	0,0238	0,0259	0,0245

Критерий однородности Лемана-Розенблатта. Критерий однородности Лемана-Розенблатта представляет собой критерий типа . Критерий был предложен в работе [10] и исследован в [11]. Статистика критерия имеет вид [3]

,

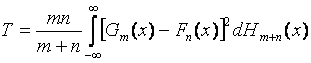где   – эмпирическая функция распределения, построенная по вариационному ряду объединения двух выборок. Статистика  используется в форме 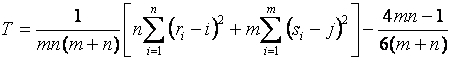[3]

,           (3)  

где  – порядковый номер (ранг) ,   – порядковый номер (ранг)  в объединенном вариационном ряде.

В [11] было показано, что статистика (3) в пределе распределена как :

.

В отличие от статистики критерия Смирнова распределение статистики  быстро сходится к предельному  [3]. Наши результаты моделирования условных распределений  статистики (3) при различных объемах выборок показали, что уже при  распределение статистики  очень близко к , а при  и  практически совпадает с ним.

Рис. 5 иллюстрирует полученные в результате моделирования условные распределения статистики  при справедливости . На основании этих распределений можно оценить значения мощности критерия Лемана-Розенблатта при различных значениях объемов выборок  и .

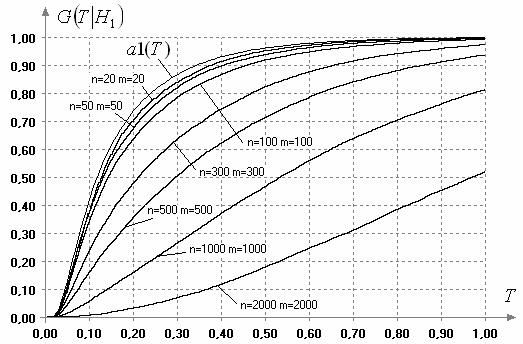
Рис. 5. Распределения статистики (3) при справедливости

Аналогичным образом были построены распределения статистики , , ,  при справедливости соответствующих конкурирующих гипотез. Вычисленные значения мощности  критерия Лемана-Розенблатта представлены в таблице 3.

Заключение. Сравнивая мощность критериев относительно рассмотренных альтернатив с учетом действительных уровней значимости критерия Смирнова (табл. 2), можно заметить, что, как правило, мощность критерия Лемана-Розенблатта заметно выше мощности критерия Смирнова. Однако относительно очень близких альтернатив несколько выше оказывается мощность критерия Смирнова (см. мощность относительно альтернативы ). Последнее становится интуитивно понятным, если вспомнить, что в критерии Смирнова мера отклонения линейная, а в критерии Лемана-Розенблатта – квадратичная.

Таблица 3. Мощность критерия однородности Лемана–Розенблатта относительно альтернатив ÷ в зависимости от объемов выборок ()

Уровень значимости	Значения мощности относительно альтернативы
	n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,1241	0,1382	0,1727	0,3125	0,4369	0,6874	0,9114
0,05	0,0615	0,0770	0,0999	0,2078	0,3211	0,5703	0,8469
0,025	0,0324	0,0410	0,0590	0,1333	0,2288	0,4589	0,7681
	Значения мощности относительно альтернативы
0,1	0,4321	0,7628	0,9549	1	1	1	1
0,05	0,3121	0,6473	0,9154	1	1	1	1
0,025	0,2120	0,5355	0,8661	0,9998	1	1	1
	Значения мощности относительно альтернативы
0,1	0,1096	0,1107	0,1147	0,1459	0,1898	0,3265	0,6237
0,05	0,0508	0,0567	0,0563	0,0691	0,0945	0,1675	0,3986
0,025	0,0252	0,0291	0,0283	0,0334	0,0442	0,0805	0,2259
	Значения мощности относительно альтернативы
0,1	0,1655	0,2875	0,5513	0,9875	0,9999	1	1
0,05	0,0801	0,1437	0,3199	0,9470	0,9993	1	1
0,025	0,0361	0,0727	0,1687	0,8587	0,9952	1	1
	Значения мощности относительно альтернативы
0,1	0,1087	0,1069	0,1135	0,1422	0,1826	0,2978	0,5463
0,05	0,0511	0,0549	0,0581	0,0668	0,0910	0,1450	0,3390
0,025	0,0241	0,0276	0,0290	0,0332	0,0431	0,0712	0,1822

При обработке результатов измерений, в задачах статистического управления качеством обычно имеют дело с выборками достаточно ограниченного или, чаще, малого объема. Следует отчетливо понимать, что критерии однородности вследствие низкой мощности при малых объемах выборок не способны различать близкие альтернативы. Поэтому проверяемая гипотеза об однородности выборок, даже в случае ее несправедливости, чаще не будет отклоняться. Сдвиг на  или увеличение масштабного параметра (рассеяния) на 10%  при малых объемах выборок критерии однородности вернее всего “не заметят”, но большие отклонения в законах, соответствующих выборкам, будут отмечаться. Например, для того чтобы в случае применения критерия Лемана-Розенблатта вероятности ошибок 1-го  и 2-го рода  не превышали 0.1 при наличии сдвига  (альтернатива ) объемы выборок должны быть порядка 2000. А при сдвиге  (Альтернатива ) вероятности ошибок не превысят величин  0.1 при объемах выборок не более 100.

Так как распределение статистики (3) очень быстро сходится к распределению , то использование его в качестве распределения статистики критерия Лемана-Розенблатта корректно и при малых   и .

В случае критерия Смирнова из-за ступенчатого характера распределения статистики (1) (особенно при =) использование предельного распределения Колмогорова  для экспериментатора будет связано с очень приблизительным знанием действительного уровня значимости (вероятности ошибки 1-го рода) и соответствующего критического значения. Поэтому при построении процедур проверки однородности по критерию Смирнова рекомендуется: 1) выбирать  так, чтобы они представляли собой взаимно простые числа, а их наименьшее общее кратное  было максимальным и равным ; 2) использовать в критерии Смирнова статистику вида (2). Тогда применение распределения Колмогорова в качестве распределения статистики (2) критерия Смирнова будет корректным при относительно малых   и .

Подводя итоги и учитывая результаты сравнительного анализа мощности и особенности применения, для проверки однородности целесообразно рекомендовать применение и того, и другого критерия.

Работа выполнена при поддержке Министерства образования и науки РФ (код проекта 15378).

1. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3.- С.3-15.

2. Лемешко Б.Ю., Лемешко С.Б., Миркин Е.П. Исследование критериев проверки гипотез, используемых в задачах управления качеством // Материалы VII международной конференции “Актуальные проблемы электронного приборостроения” АПЭП-2004. Новосибирск, 2004. – Т. 6. – С. 269-272.

3. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

4. Лемешко Б.Ю., Миркин Е.П. Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. № 10. – С. 10-16.

5. Орлов А.И. О проверке однородности двух независимых выборок // Заводская лаборатория. – 2003. – Т.69. №.1. – С.55-60.

6. Смирнов Н.В. Оценка расхождения между эмпирическими кривыми распределения в двух независимых выборках // Бюллетень МГУ, серия А. –  1939. – Т.2. №2. – С.3-14.

7. Боровков А.А. К задаче о двух выборках // Изв. АН СССР, серия матем., 1962. Т. 26. – С.605-624.

8. Королюк В.С. Асимптотический анализ распределений максимальных уклонений в схеме Бернулли // Теория вероятностей и ее применения. – 1959. – Т.4. – С. 369-397.

9. Смирнов Н.В. Вероятности больших значений непараметрических односторонних критериев согласия // Труды Матем. ин-та АН СССР. – 1961. – Т.64. – С. 185-210.

10. Lehmann E.L. Consistency and unbiasedness of certain nonparametric tests / Ann. Math. Statist. – 1951. V.22. № 1. – P.165-179.

11. Rosenblatt M. Limit theorems associated with variants of the von Mises statistic // Ann. Math. Statist. – 1952. V.23. – P.617-623.