См. также: Прикладная математическая статистика (материалы к семинарам)

 

Научный вестник НГТУ. - 2006. - № 2(23)

 

 

УДК 62-83: 531.3

Исследование распределений статистик, используемых для проверки гипотез о равенстве дисперсий при законах ошибок наблюдений, отличных от нормального*

Б.Ю. Лемешко, В.М. Пономаренко

Методами статистического моделирования исследуются распределения статистик критериев Хартли и критерия, предложенного Шеффе, при нарушении предположений о нормальном законе рас­пределения ошибок наблюдений. Исследуется мощность критериев. Исследуется мощность критерия Шеффе в условиях нарушения предположения о нормальности. Приводятся рекомендации по исполь­зованию данных критериев.

1. Введение

Проверка гипотез в классическом дисперсионном анализе базируется на ряде предположений [1,2], и одно из основных – предположение о нормальном за­коне ошибок наблюдений. В рамках этих предположений оказалось возможным аналитически вывести предельные распределения ряда статистик.

Очевидно, что наблюдаемые данные далеко не всегда подчиняются нор­мальному закону. В такой ситуации правомерно возникает вопрос, насколько кор­ректным оказывается применение классического аппарата проверки гипотез о средних, о дисперсиях или методов множественного сравнения? В каких случаях можно без боязни использовать классические критерии, а когда их применение чревато неверными выводами, и как следует поступать в таких ситуациях?

В ряде работ [1,3] приводятся результаты теоретических и численных ис­следований устойчивости различного рода критериев проверки гипотез по отно­шению к виду наблюдаемого закона. Данные источники содержат указания на су­щественную зависимость от вида закона критериев, касающихся проверки гипотез о дисперсиях, и на слабую зависимость в этом же случае критериев проверки ги­потез о средних.

Применение компьютерных технологий моделирования [4,5] позволяет исследовать статистические свойства критериев в условиях нарушения клас­сиче­ских предположений. Построение моделей распределений статистик при раз­лич­ных законах распределения ошибок расширяет аппарат и область применения как дисперсионного, так и многих других видов анализа.

Ранее нами проводились исследования статистик критериев диспер­сион­ного анализа, используемых для проверки гипотез о средних  в моделях с по­стоян­ными уровнями факторов [6,7], для проверки гипотез о дисперсиях в моделях с случайными уровнями факторов [8], проводились исследования, касающиеся про­верки гипотез о равенстве дисперсий в задачах контроля качества [9].

Данная работа продолжает исследования устойчивости критериев про­вер­ки гипотез о равенстве дисперсий. Нами рассматривается два критерия. Во-пер­вых, крите­рий Хартли [10], который во многом подобен традиционным критериям проверки однородности дисперсий, таким как критерий Кокрена и Бартлетта. Во-вторых, приближенный критерий проверки однородности дисперсий, предложен­ный Шеффе (далее критерий Шеффе), который по предположению автора [1] дол­жен быть очень устойчив к нарушению предположений о нормальности.

Цель проводимых исследований заключалась в следующем. Во-первых, установлении того, что происходит с распределениями классических статистик, используемых в моделях с постоянными уровнями факторов для проверки гипо­тезы о равенстве дисперсий, если наблюдаемый закон в той или иной мере отлича­ется от нормального. Во-вторых, в проверке, насколько будут корректны стати­стические выводы, базирующиеся на классических результатах, если нарушено предположение о нормальности. И, в-третьих, в создании необходимого матема­тического аппарата, обеспечивающего исследова­телю корректность выводов при законах распределения, существенно отличающихся от нормального.

2. Постановка задачи

Критерии однородности дисперсий в дисперсионном анализе принято рас­сматривать для однофакторной модели вида:

 

, , ,                           (1)

 

где  – средние отклика  на  уровнях фактора,  – число наблюдений на -м уровне, общее число наблюдений в модели составляет . В этом случае совокупности наблюдений  при различных значениях  могут рас­сматриваться как элементы выборок из  генеральных совокупностей с матема­тическим ожиданием равным , дисперсией  для -той генеральной совокупности. В классической постановке предполагается, что все наблюдения распределены по нормальному закону.

Проверяемая гипотеза имеет вид

 

,                                           (2)

 

а конкурирующая с ней –

 

,                                                    (3)

 

где неравенство выполняется, по крайней мере, для одной пары индексов  и .

Критерий Хартли был предложен для случая сбалансированного плана на­блюдений, т.е. для случая, когда . Статистика критерия имеет вид [10]

 

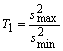,                                                (4)

где

 

,    ,    ,    .

 

В [10] приводятся процентные точки условного распределения статистики (4) в случае справедливости проверяемой гипотезы и нормального закона ошибок на­блюдения модели (1).

Критерий Шеффе может применяться при анализе моделей как со сбалан­сированным, так и с несбалансированным планом наблюдений. В критерии Шеффе статистика опирается не на собственно оценки дисперсий, как это обстоит в случае критериев Хартли, Кокрена и Бартлетта, а на средние значения логариф­мов оценок дисперсий. При таком подходе задача сводится к сравнению средних, а критерии проверки гипотез “о средних” устойчивы по отношению к форме рас­пределения ошибок наблюдений. Применяемое логарифмирование позволяет при­близить распределение к нормальному закону.

Чтобы перейти к сравнению средних, каждая -я выборка наблюдений , , разбивается на  групп объемом , так что . Обозна­чим для удобства совокупность значений, полученную путем рас­пре­деле­ния значений  на подвыборки, через

 

, , , .                   (5)

 

Тогда статистика критерия Шеффе [1] может быть записана в следующем виде:

 

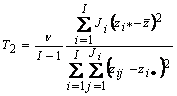,                              (6)

 

где

 

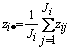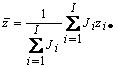, , .                            (7)

 

Значения , выступающие в роли исходных наблюдаемых значений для критерия сравнения средних со статистикой (6) вычисляются как

 

,                                                  (8)

 

где – выборочная дисперсия подгруппы, определяемая по формуле

 

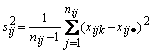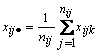, .                    (9)

 

По предположению Шеффе статистика  должна подчиняться -распре­делению Фишера со степенями свободы  и . Причем распределение статистики не должно существенно зависеть от закона распределения ошибок , поскольку критерий строился как устойчивый к нарушению предположений о нормальности.

3. Условия проведения экспериментов

При верной нулевой гипотезе дисперсия ошибок наблюдения ,  (без потери общности) задавалась равной единице, значения средних от­клика на уровнях  (также без потери общности) задавались равными нулю. Выбо­рочные значения наблюдений  формировались в соответствии с видом мо­дели (1).

Исследования распределений статистик проводились при различных зако­нах ошибок наблюдений и случайного фактора модели (1). В данном случае при­водятся результаты исследований, когда ошибки наблюдений подчинялись сле­дующим законам: нормальному, распределению максимальных значений, семей­ству симметричных распределений с плотностью

 

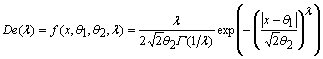              (10)

 

при различных значениях параметра формы . Распределение  включает в качестве частных случаев распределение Лапласа (=1) и нормальное (=2). В данной работе приводятся результаты исследований распределений статистик в случае принадлежности наблюдений семейству , как правило, при значе­ниях параметра формы =0.5, 1, 5, 10.

Использование распределений из семейства  для моделирования оши­бок наблюдения позволяет задавать симметричные законы распределения раз­личной формы, изменяя значения параметра : чем меньше параметр , тем “тяже­лее” хвосты распределения , чем больше параметр , тем хвосты “легче”. Распределение максимальных значений использовалось для выявления влияния на распределения статистик асимметричности закона.

При исследовании поведения статистики критерия Хартли рассмат­ри­ва­лось также логистическое распределение. В этом случае выяснялось поведение распределения статистики при “малых” отклонениях от нормальности.

При проведении экспериментов по моделированию распределений стати­стик объем моделируемых выборок исследуемых статистик составлял, как пра­вило, величину .

Для контроля правильности результаты моделирования сравнивались с из­вестными аналитическими или численными, полученными другими авторами для «классической» ситуации принадлежности наблюдений нормальному закону. В частности, для критерия Хартли при различных объемах выборок моделировались выборочные квантили, которые сравнивались с табличными [10] значениями про­центных точек. А в случае критерия Шеффе эмпирическое распределение стати­стики (6) сравнивалось с теоретическим распределением Фишера, в соответствии с которым приближенно распределена статистика (6).

Количественной мерой близости эмпирических распределений статистик соответствующим теоретическим функциям распределения при проверке согласия служили достигнутые уровни значимости  для применяемых критериев согласия, где  – значение статистики  используемого критерия, вычисленное по конкретной выборке исследуемых статистик. Проверка согласия осущес­твля­лась по критериям  Пирсона, Колмогорова,  Крамера-Мизеса-Смирнова,  Андерсона-Дарлинга [11, 12].

В тех случаях, когда при исследовании критерия Шеффе не наблюдалось согласия эмпирического распределения с соответствующим распределением Фи­шера, и каждый раз при исследовании критерия Хартли, строилась приближенная модель для полученного эмпирического распределения статистики. Аппроксима­ция предельного закона распределения статистики формировалась как усреднен­ное по параметрам распределение, полученное на основании десяти эксперимен­тов.

Как при проверке согласия с известным распределением, так и при по­строении модели распределений, использовалась программная система ISW, в рамках которой реализованы результаты, полученные с помощью методики ком­пьютерного моделирования, развиваемой на кафедре Прикладной математики НГТУ [13].

4. Исследование распределений статистики

Проверка корректности моделирования проводилась путем сравнения зна­чений, взятых из таблиц верхних процентных точек распределения статистики (4) в нормальном случае, и выборочных квантилей, полученных при различных объе­мах смоделированных выборок статистик.

Значения табличных и выборочных квантилей, также как и точность по­лученных выборочных квантилей при  = 200000, представлены в таблице 1. При­водимые значения квантилей являются усредненными по 10 экспериментам. Из таблицы видно, что в пределах точности, достигаемой при используемых объе­мах выборок статистик, получаемые процентные точки весьма близки к таблич­ным значениям, с которыми производится сравнение. В целом это позволяет гово­рить о корректности используемой методики моделирования.

 

Таблица 1

Табличные и выборочные (с оценкой точности при  = 200000) квантили распреде­ления статистики (4) в случае нормального распределения ошибок на­блюдения при различных значениях  и , различных объемах  выборки стати­стик

Размер-ность задачи

Значение

Табличное значение

Выборочные кван­тили при различных объемах выборок статистик

Точность выборочных квантилей,

 = 200000

 =

10000

 = 200000

=3, =5

0.05

15.5

15.48

15.38

0.195

0.01

37

36.41

36.19

0.732

=3, =61

0.05

1.85

1.84

1.84

0.005

0.01

2.22

2.14

2.14

0.010

=12, =5

0.05

51.4

50.50

51.05

0.754

0.01

120

118.17

118.77

3.496

=12, =61

0.05

2.36

2.35

2.35

0.005

0.01

2.7

2.67

2.67

0.011

 

Рисунок 1 иллюстрирует поведение распределения статистики при нару­шении предположений нормальности. Из рисунка видно, что на распределение статистики (4) сильно влияет закон распределения наблюдений . Чем “тяже­лее” хвосты, тем ниже и правее от “нормального” случая находится распределение статистики.

Для ряда значений  и  построены модели распределения статистики (4) при различных законах ошибок наблюдения.

 

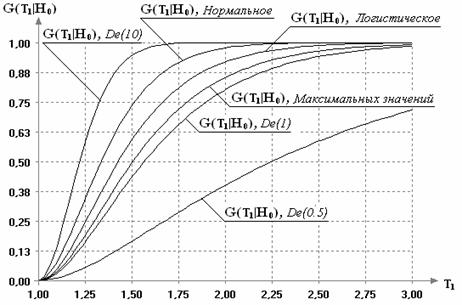
Рис. 1. Эмпирические функции распределения статистики (4) в случае =3, =61 при различных законах ошибок наблюдений

5. Исследование распределений статистики

При использовании критерия Шеффе для проверки гипотезы однородно­сти дисперсий (2) имеющееся число наблюдений на уровне фактора , как это видно из формул (5)-(9), может иметь различные разбиения на подгруппы ( - число подгрупп и  - число наблюдений в подгруппе). При этом в [1] делается предположение о том, что статистика (6) приближенно будет подчиняться -рас­пределению Фишера с числом степеней свободы  и . В случае сбалансированного плана наблюдений, который рассматривается в данной работе, имеем распределение , где  - одно и тоже для всех . Возни­кает вопрос: при каких значениях  и  при нормальном законе распреде­ления ошибок наблюдается достаточно хорошее согласие распределения статистики (6) и распределения , чтобы при проверке гипотезы (2) можно было  пользоваться этим -распределением для вычисления достигнутых уровней значимости.

В таблице 2 приведены достигнутые уровни значимости, полученные при проверке согласия эмпирического распределения статистики (6) при выполнении предположений о нормальности и соответствующего теоретического распределе­ния Фишера. В таблице указаны достигнутые уровни значимости для минималь­ных значений , при которых уже наблюдается некоторое согласие сравнивае­мых распределений для ряда заданных значений  и  (одно и тоже для всех). Это согласие трудно назвать хорошим. Но, как иллюстрирует рисунок 2, уже при таких значениях  использование соответствующего -распределения в каче­стве предельного распределения статистики (6) не приведет к большим ошибкам при вычислении соответствующих вероятностей. Из рисунка также видно, что эм­пирические распределения, полученные в случае размерностей, представленных в таблице 2, и в случае значений , больше приведенных (а значит и больших значе­ний ), практически сливаются.

Как показывают исследования, согласие эмпирических и соответ­ству­ю­щих теоретических распределений статистики (6) растет с ростом . Это дает осно­вания считать уровень согласия, отражаемый в таблице 2 (минимально) до­пустимым для того, чтобы уже при таких объемах выборок рекомендовать подхо­дящее -распределение к использованию в качестве предельного распределения статистики (6).

 

Таблица 2

Значения достигнутых уровней значимости, полученных в результате проверки со­гласия эмпирических распределений статистики (6) с соответствующими -распре­делениями при справедливости гипотезы  вида (2) и нормальном законе ошибок наблюдений

Критерий

согласия

Размерность задачи;

распределение, с которым проверяется согласие

=2,=2, =5;

=2,=5 =4;

=5,=2, =6;

=5, =5, =4;

Отн. правдоподобия

 Пирсона 

Колмогорова 

 Мизеса 

 Анд.-Дарлинга

0.22

0.22

0.22

0.24

0.24

0.21

0.21

0.11

0.09

0.09

0.14

0.14

0.18

0.16

0.12

0.12

0.12

0.16

0.16

0.14

 

 

Было исследовано, при каких значениях  ( и ) при заданном значе­нии  и нормальном законе ошибок наблюдений достаточно высока бли­зость эмпирического распределения статистики (6) и соответствующего теорети­ческого распределения Фишера. Рассматривались значения  в диапазоне от 2 до 5,  в диапазоне от 2 до 6.

По результатам исследований сделаны следующие заключения. Мини­мальное значение , при котором допустимо использовать -распределение в ка­честве предельного распределения статистики (6), составляет 10-12 наблюдений в группе.

Необходимый для приемлемого согласия объем  в наибольшей степени определяется выбором числа . Например, при =2 минимально допустимый объем  составляет 10-12, при =4 – 16-20, а при =6  –  20-25.

В целом следует отметить, что при нормальном законе ошибок и числе наблюдений  в группах около 30, можно без риска совершения больших ошибок использовать -распределение в качестве предельного распределения статистики (6) при условии, что будет выбрано разбиение, в котором .

Но, если объем выборок  меньше этого числа, что довольно часто встреча­ется в дисперсионном анализе, то для того, чтобы распределение стати­стики (6) хорошо согласовалось с соответствующим -распределением, следует выбирать такое разбиение на подгруппы, чтобы  было наибольшим, а  - наи­меньшим из возможных.

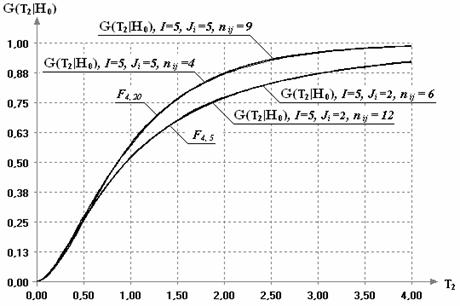
Рис. 2. Эмпирические и теоретические функции распределения статистики (6) в случае нор­мального закона ошибок наблюдения при =5 и различных значениях  и  

 

В таблице 3 для случая =5, =5, =4 представлены достигнутые уровни значимости при проверке согласия получаемых в результате модели­рова­ния эмпирических распределений статистики (6) и предполагаемого -распреде­ления Фишера при отличных от нормального законах наблюдений .

Из таблицы следует, что на самом деле распределение  оказывает влияние на степень согласия эмпирических распределений статистики (6) с рас­пределениями Фишера. В случае распределения с "тяжелыми" хвостами (напри­мер, ) наблюдается очень высокая степень согласия эмпирических распреде­лений статистики (6) и -распределения, по которому должна быть приблизительно распределена статистика (6) в “нормальном” случае. Из таблицы 3 видно, что в случае распределения наблюдений по закону  степень согла­сия распределения статистики (6) с -распределением существенно выше, чем в нормальном случае. В случае принадлежности наблюдений распределению мак­симальных значений – несколько выше, чем в нормальном случае. А вот при ошибках наблюдений по законам с "легкими" хвостами, например,  и  согласие распределения статистики (6) с -распределением  при =5, =4 уже практически не наблюдается. Причем согласие тем хуже, чем бо­лее "легкими" хвостами обладает закон распределения ошибок.

Таблица 3 иллюстрирует также влияние разбиения на подвыборки в слу­чае принадлежности ошибок наблюдения законам, отличным от нормального. Из таблицы видно, что при увеличении  (при постоянном ) согласие распре­деления статистики (6) с -распределением  растет в случаях ошибок с несим­метричными законами и законами с «легкими» хвостами. При этом в случае =2, =10 при законах распределения  и  согласие достигает прием­лемого уровня.

В целом результаты исследований позволяют рекомендовать при разбие­нии наблюдений на подгруппы делать это так, чтобы  объем подгруппы  был мак­симален. Причем данная рекомендация справедлива как в случае нормального закона ошибок наблюдений, так и для ситуаций, когда ошибки наблюдений под­чиняются законам распределения, отличным от нормального.

 

 

Таблица 3

Значения достигнутых уровней значимости, полученных в результате проверки согласия эмпирического распределения статистики (6) с теоретическим -распределением при справедливости гипотезы  вида (2) при =5, =20, при различных разбиениях на подвыборки и различных законах ошибок наблюдений

,

Критерий

согласия

Распределение ошибок наблюдений

=5, =4

Отн. правдоподобия

 Пирсона

Колмогорова

 Мизеса

 Анд.-Дарлинга

0.2162

0.2176

0.1526

0.1896

0.1751

0.5199

0.5195

0.5431

0.5291

0.5158

0.0034

0.0037

0.0395

0.0323

0.0112

0.0014

0.0014

0.0399

0.0225

0.0078

=2, =10

Отн. правдоподобия

 Пирсона

Колмогорова

 Мизеса

 Анд.-Дарлинга

0.434

0.433

0.525

0.526

0.523

0.374

0.374

0.388

0.358

0.312

0.078

0.078

0.142

0.132

0.093

0.109

0.109

0.171

0.146

0.125

 

 

Исследования показали, что наблюдаемые различия в степени близости распределения статистики (6) и соответствующего распределения Фишера при различных законах наблюдений , объясняется тем, как распределены , непосредственно входящие в статистику  (6). Распределение  стано­вится тем симметричнее, чем "тяжелее" хвосты распределения наблюдений . Так, в случае принадлежности   закону  распределение  наи­более симметрично, в случае принадлежности  закону  распределе­ние  наименее симметрично.

6. Исследование мощности критериев Хартли и Шеффе

В таблице 4 приведены значения мощности для 4-х критериев проверки однородности дисперсий: Шеффе, Хартли, Бартлетта и Кокрена при достаточно больших объемах выборок =200 и =500. Данные по критериям Бартлетта и Кокрена взяты из работы [9]. При этом для критерия Шеффе для каждого набора значений =5 и  приведены значения мощности, полученные при различных спо­собах разбиения на подгруппы. Рассматривается альтернатива , дос­таточно близкая к проверяемой гипотезе  вида (2).

Анализируя данные таблицы 4, можно сделать несколько выводов. Во-первых, если мощность критерия Хартли в целом сравнима с мощностью критерия Бартлетта, то мощность критерия Шеффе в большинстве случаев ниже мощности остальных рассматриваемых критериев. Во-вторых, мощность критерия Шеффе очень сильно зависит от того, как именно разбить  наблюдений на  число под­групп по  наблюдений в каждой. В большинстве случаев наблюдается сле­дующая тенденция: мощность возрастает при увеличении числа подгрупп , но может резко упасть при слишком большом значении , как в случае =50, =10.

 

Таблица 4

Мощность критериев Кокрена, Бартлетта, Шеффе и Хартли относительно альтер­нативы вида :  при =5 и различных значениях  в случае нор­мального закона ошибок наблюдений

Разбиение на подгруппы в случае критерия Шеффе

Критерий  Шеффе

Критерий  Хартли

Критерий  Бартлетта

Критерий

Кокрена

0.1

200

=2, =100

0.542

0.846

0.835

0.920

=10, =20

0.762

=20, =10

0.735

500

=5, =100

0.987

0.997

0.997

0.999

=10, =50

0.992

=50, =10

0.266

0.05

200

=2, =100

0.362

0.760

0.757

0.837

=10, =20

0.647

=20, =10

0.619

500

=5, =100

0.967

0.993

0.993

0.997

=10, =50

0.981

=50, =10

0.172

0.01

200

=2, =100

0.111

0.535

0.556

0.671

=10, =20

0.390

=20, =10

0.373

500

=5, =100

0.853

0.965

0.970

0.986

=10, =50

0.920

=50, =10

0.062

 

В таблице 5 представлены значения мощности критериев Шеффе и Хартли, полученные для альтернатив вида  при различных значениях  в случае различных объемов выборок . Как и ожидалось, при близких альтернати­вах (=1.2, =1.44) и относительно небольшом числе наблюдений в группах: =50 и =20, мощность критериев Шеффе и Хартли уже крайне низка. Приемлемым уровень мощности становится в случае альтернатив, при которых дисперсии отличаются в «разы». Причем у критерия Шеффе при =20 мощность все еще очень низка.

 

 

Таблица 5

Мощность критериев Шеффе и Хартли относительно альтернативы вида :  при =5 в случае нормального закона распределения

С

,  для критерия Шеффе

 

0.1

0.05

0.01

 

Шеф-фе

Харт-ли

Шеф-фе

Харт-ли

Шеф-фе

Харт-ли

1.2

500

=10, =50

0.590

0.655

0.455

0.532

0.221

0.296

200

=10, =20

0.290

0.343

0.185

0.232

0.060

0.087

50

=5, =10

0.136

0.163

0.072

0.092

0.016

0.024

20

=4, =5

0.107

0.130

0.054

0.069

0.011

0.015

1.44

500

=10, =50

0.992

0.997

0.981

0.993

0.920

0.965

200

=10, =20

0.762

0.846

0.647

0.760

0.390

0.535

50

=5, =10

0.255

0.324

0.155

0.215

0.045

0.077

20

=4, =5

0.142

0.178

0.075

0.101

0.017

0.026

3

50

=5, =10

0.946

0.992

0.894

0.983

0.700

0.937

20

=4, =5

0.519

0.802

0.375

0.701

0.149

0.445

 

 

Исследования показали (см. таблицу 6), что на мощность критерия Шеффе также влияет закон распределения наблюдений . Чем “легче” хвосты распреде­лений, тем выше мощность, и наоборот: чем хвосты “тяжелее”, тем ниже мощность. Влияние на распределение статистики (6) при верной альтернативе не­симметричности распределения схоже с влиянием распределения с более “тяже­лыми”, чем у нормального закона хвостами. Рисунок 3 иллюстрирует влияние за­кона распределения наблюдений на распределение статистики при справедливости конкурирующей гипотезы и большом объеме выборки =500.

Но при малых объемах , как видно из таблицы 6, мощность уже на­столько мала, что различия, обусловленные видом закона ошибок наблюдений , незначительны.

 

 

 

 

Таблица 6

Мощность критерия Шеффе при =5 при различных объемах  относительно альтернативы вида :  при различных законах ошибок наблюдений

,

Распределение ошибок наблюдения

=10, =50

0.1

0.163

0.160

0.590

0.837

0.897

0.05

0.091

0.090

0.455

0.740

0.822

0.01

0.023

0.022

0.221

0.494

0.605

=5, =10

0.1

0.107

0.105

0.136

0.159

0.169

0.05

0.054

0.053

0.072

0.087

0.093

0.01

0.011

0.011

0.016

0.021

0.0226

 

 

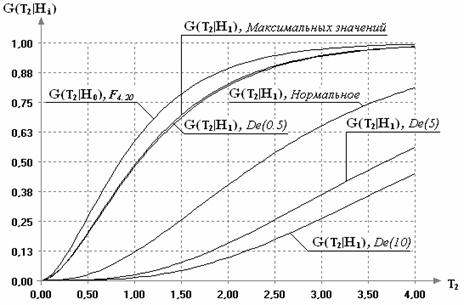
Рис. 3. Функции распределения статистики (6) в случаях справедливости проверяемой гипотезы  вида (2) и справедливости конкурирующей гипотезы  вида  при различных законах наблюдений, при =5, =10, =50

Заключение

Как показали исследования, критерий Хартли крайне чувствителен к за­кону распределения наблюдений.

В отличие от него, критерий Шеффе действительно достаточно устойчив к нарушению предположений о нормальности. В то же время вид закона ошибок на­блюдений влияет на объем выборки, при котором достигается достаточно хорошее согласие распределения статистики с распределением Фишера. Чем “легче” хво­сты распределений, тем большие объемы выборок требуются для достаточно хо­рошего согласия.

Мощность критерия Хартли в нормальном случае сравнима с мощностью критерия Бартлетта, ниже мощности критерия Кокрена и выше мощности крите­рия Шеффе.

Мощность критерия Шеффе ниже мощности других критериев и зависит от того, каким именно образом наблюдения разбиваются на подгруппы.

Сложен выбор оптимальных значений  и  при заданном , так как он зависит от вида закона распределения ошибок наблюдения. Если ошибки под­чиняются закону с «легкими» хвостами, например, законам  или , то следует выбирать разбиение на подгруппы с минимальным значением . Это позво­лит с большей уверенностью использовать распределение Фишера в качестве предельного распределения статистики (6). Если же у закона распределения оши­бок «тяжелые» хвосты, то следует выбирать разбиение с достаточно большим зна­чением . Это позволит увеличить, малую в этих случаях, мощность критерия. Таким образом, наиболее удачное разбиение зависит от вида закона распределения ошибок.

В целом по критерию Шеффе можно сделать следующий вывод: свойства критерия зависят от закона ошибок наблюдения и от того, насколько удачно вы­брано разбиение на подвыборки.

СПИСОК ЛИТЕРАТУРЫ

[1] Шеффе Г. Дисперсионный анализ. - М.: Физматгиз, 1980. - 628 с.

[2] Маркова Е.В. и др. Дисперсионный анализ и синтез планов на ЭВМ. - М.: Наука, 1982.-195 с.

[3] Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука,1973. - 900 с.

[4] Лемешко Б.Ю. Компьютерные методы исследования статистических закономерностей // Ин­формационные системы и технологии: ИСТ`2000: Сб. научн. ст. - Новосибирск. 2001. - С.26-41.

[5] Лемешко Б.Ю., Постовалов С.Н. Компьютерное моделирование как способ познания стати­стических закономерностей в технике, экономике, естествознании // Материалы региональной конфе­ренции “Вероятностные идеи в науке и философии”. - Новосибирск: Ин-т философии и права СО РАН / НГУ. 2003. - С. 110-113.

[6] Лемешко Б.Ю. Пономаренко В.М. Проблемы применения классического аппарата дисперси­онного анализа в приложениях технического, экономического и естественно-научного характера // Ма­териалы региональной конференции (с участием иностранных ученых) “Вероятностные идеи в науке и философии”. - Новосибирск: Ин-т философии и права СО РАН / НГУ. 2003. - С. 106-109.

[7] Lemeshko B.Yu., Ponomarenko V.M. Statistical Hypotheses Testing In Variance Analysis In Case Of Classical Assumptions Failure // Proceedings of the Seventh International Conference “Computer Data Analysis and Modeling: Robustness and Computer Intensive Methods”, September 6-10, 2004, Minsk. Vol. 1. - P. 110-113.

[8] Лемешко Б.Ю. Пономаренко В.М. Проверка гипотез в моделях дисперсионного анализа со случайными факторами при нарушении предположений о нормальности / Доклады АН ВШ РФ, № 2(5).- С. 26-39

[9] Лемешко Б.Ю., Миркин Е.П. Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. № 3. - С. 10-16.

[10] Закс Л. Статистическое оценивание. // Пер. с нем. В.Н. Варыгина / Под ред. Адлера Ю.П., Горского В.Г.. - М.: “Статистика”, 1976. - 598 с.

[11] Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. — М.: Изд-во стандартов, 2002. — 87 с.

[12] Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. — М.: Изд-во стандартов,2002. — 64 с.

[13] Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Про­граммная система. - Новосибирск: Издательство НГТУ, 1995. - 125 с.


* Статья получена 20 марта 2006 г.

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а)