Кластеризация
данных при помощи нечетких отношений в Data Mining
Введение
Кластеризация – это один
из методов исследования Data Mining
(“раскопки
данных”). Методы кластерного анализа позволяют разделить изучаемую совокупность
объектов на группы “схожих” объектов, называемых кластерами, разнести записи в
различные группы, или сегменты.
Большинство алгоритмов кластеризации не опираются на традиционные для
статистических методов допущения; они могут использоваться в условиях почти
полного отсутствия информации о законах распределения данных. Кластеризацию
проводят для объектов с количественными (числовыми), качественными или
смешанными признаками.
Существует множество
методов кластеризации, которые можно классифицировать на четкие и нечеткие.
Четкие методы кластеризации разбивают исходное множество объектов X на
несколько непересекающихся подмножеств. При этом любой объект из X
принадлежит только одному кластеру. Нечеткие методы кластеризации позволяют
одному и тому же объекту принадлежать одновременно нескольким (или даже всем)
кластерам, но с различной степенью. Нечеткая кластеризация во многих ситуациях
более "естественна", чем четкая, например, для объектов,
расположенных на границе кластеров.
Методы кластеризации
также классифицируются по тому, определено ли количество кластеров заранее или
нет. В последнем случае количество кластеров определяется в ходе выполнения алгоритма
на основе распределения исходных данных. В начале рассмотрим алгоритм
c-средних, разбивающий данные на наперед заданное число кластеров, а затем
алгоритм горной кластеризации, который не требует задания количества кластеров.
1.Математические основы разделения на классы
Для начала рассмотрим математические основы разделения на классы.
Пусть X – метрическое пространство
и ![]() определенная на нем метрика,
определенная на нем метрика, ![]() - последовательность элементов из X.
- последовательность элементов из X.
Мы предполагаем
далее, что ![]() (1.1)
(1.1)
Из условия (1.1)
следует, что ![]() справедливо:
справедливо:
![]() (1.2)
(1.2)
Таким образом, для каждого индекса i мы можем определить функцию, описывающую меру сходства j-ого элемента последовательности с i-ым элементом:
![]()
![]() (1.3)
(1.3)
Для каждого индекса i определим функцию, описывающую меру сходства k-ого и l-ого элемента относительно i-ого элемента:
![]()
![]() , (1.4)
, (1.4)
Определим теперь функцию, описывающую меру сходства любых двух элементов последовательности относительно всех элементов последовательности:
![]() ,
,
![]() (1.5)
(1.5)
Доказательство: ![]() для всех k и i, следовательно
для всех k и i, следовательно ![]()
Доказательство: ![]() , следовательно
, следовательно ![]()
Для k=1,2,…,n
определим рекурсивно функции ![]()
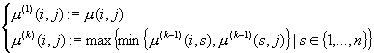 (1.8)
(1.8)
Доказательство: Доказательство по индукции по k.
При k = 1
утверждение следует из определения ![]() и (1.6).
и (1.6).
Пусть утверждение
справедливо для k-1. Тогда из (1.8)
следует 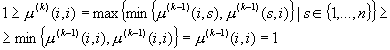
Т.е. утверждение доказано.
Доказательство: Доказательство по индукции по k.
При k = 1
утверждение следует из определения ![]() и (1.7).
и (1.7).
Пусть утверждение
справедливо для k-1. Тогда из (1.8)
следует 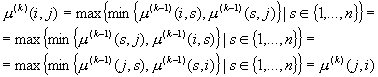
Т.е. утверждение доказано.
Доказательство:

Т.е. утверждение доказано.
Утверждение 6: Для ![]() и
и ![]() справедливо:
справедливо:![]() (1.12)
(1.12)
Доказательство: Доказательство по
индукции по k. При k = 1 нечего доказывать. Пусть утверждение справедливо для
k-1. Тогда из предположения индукции следует, что ![]() . (1.13)
. (1.13)
Из (11) следует,
что ![]() (1.14)
(1.14)
Тогда из
определения ![]() , (13) и (14) следует
, (13) и (14) следует
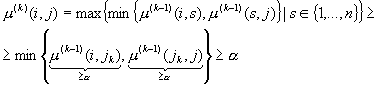
Т.е. утверждение доказано.
Утверждение 7: Пусть ![]() ,
, ![]() и
и ![]() . Тогда существует такое число m и индексы
. Тогда существует такое число m и индексы ![]() , что
, что ![]() (1.15)
(1.15)
Доказательство: Доказательство по индукции по k. При k = 1
утверждение справедливо для индекса j. Пусть утверждение справедливо для k-1.
Из определения ![]() следует существование индекса p такого, что
следует существование индекса p такого, что
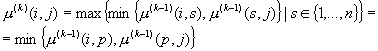 (1.16)
(1.16)
Из (16) и условия утверждения следует, что
![]() (1.17)
(1.17)
Из условия ![]() и из условия индукции следует существование индексов
и из условия индукции следует существование индексов ![]() таких, что
таких, что ![]() .
.
Аналогично, из условия ![]() и из условия индукции
следует существование индексов
и из условия индукции
следует существование индексов ![]() таких, что
таких, что ![]() .
.
Объединяя эти выводы, получаем, что утверждение доказано для
![]() и
и ![]() , где
, где 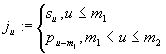
Тогда ![]() (1.18)
(1.18)
Доказательство: Из условий ![]() и (1.15) следует
существование индексов
и (1.15) следует
существование индексов ![]() и
и ![]() таких, что
таких, что
![]() и
и ![]() (1.19)
(1.19)
Так как ![]() , то из этого множества индексов можно выбрать множество,
состоящее не более чем из n индексов
(путем удаления повторяющихся элементов)
, то из этого множества индексов можно выбрать множество,
состоящее не более чем из n индексов
(путем удаления повторяющихся элементов) ![]() для которых также справедливо
для которых также справедливо ![]() (1.20)
(1.20)
Из (12) следует, что ![]() . Так как
. Так как ![]() , то из (1.11)
следует
, то из (1.11)
следует
![]() , что и требовалось доказать.
, что и требовалось доказать.
Определение
5: Для ![]() определим на
множестве
определим на
множестве ![]() бинарное отношение
бинарное отношение ![]() следующим образом:
следующим образом:
![]()
Утверждение 9:
Отношение ![]() является отношением эквивалентности
является отношением эквивалентности
Доказательство:
1. Рефлексивность.
Из (9) следует, что ![]()
2. Симметричность.
Пусть ![]() . В силу (1.10)
. В силу (1.10)
![]()
3. Транзитивность.
Пусть ![]() . Из (1.18)
следует, что
. Из (1.18)
следует, что ![]()
Таким образом, отношение
эквивалентности ![]() разбивает множество
разбивает множество ![]() на классы
эквивалентности. Два элемента
на классы
эквивалентности. Два элемента ![]() входят в один класс эквивалентности тогда и только тогда,
когда значение функции
входят в один класс эквивалентности тогда и только тогда,
когда значение функции![]() от этих элементов велико, что на основании (1.12), (1.15)
эквивалентно существованию последовательности пар элементов
от этих элементов велико, что на основании (1.12), (1.15)
эквивалентно существованию последовательности пар элементов ![]() , на которых значение функции
, на которых значение функции ![]() велико. По
определению
велико. По
определению ![]() это означает близость
элементов каждой пары друг другу. Т.е. два элемента входят в один класс
эквивалентности тогда и только тогда, когда между ними есть последовательность попарно
близких друг к другу элементов.
это означает близость
элементов каждой пары друг другу. Т.е. два элемента входят в один класс
эквивалентности тогда и только тогда, когда между ними есть последовательность попарно
близких друг к другу элементов.
2. Кластеризация при
заданном числе кластеров
Исходной информацией для
кластеризации является матрица наблюдений:
 , (2.1)
, (2.1)
Задача кластеризации
состоит в разбиении объектов из X на несколько
подмножеств (кластеров), в которых объекты более схожи между собой, чем с
объектами из других кластеров. В метрическом пространстве "схожесть"
обычно определяют через расстояние. Расстояние может рассчитываться как между
исходными объектами (строчками матрицы X), так и от этих
объектов к прототипу кластеров. Обычно координаты прототипов заранее
неизвестны - они находятся одновременно с разбиением данных на кластеры.
Нечеткие кластера
опишем матрицей нечеткого разбиения
![]() ,
, ![]()
![]() ,
, ![]() , (2.2)
, (2.2)
где ![]() -тая строчка содержит степени принадлежности объекта
-тая строчка содержит степени принадлежности объекта ![]() кластерам
кластерам ![]() . Единственным отличием матрицы степеней принадлежности
четкого разбиения о нечеткого является то, что элементы матрицы
. Единственным отличием матрицы степеней принадлежности
четкого разбиения о нечеткого является то, что элементы матрицы ![]() принимают значения из двухэлементного множества
принимают значения из двухэлементного множества ![]() , а не из интервала
, а не из интервала ![]() . Условия для матрицы выглядят следующим образом
. Условия для матрицы выглядят следующим образом
![]() для
для ![]() (2.3)
(2.3)
![]() для
для ![]() (2.4)
(2.4)
(2.3) обеспечивает, чтобы кластеры не были пустыми, (2.4) обеспечивает, чтобы все элементы из набора данных были распределены по всем кластерам, то есть сумма степеней принадлежности по всем кластерам должна быть 1 для каждого элемента данных. Алгоритмы нечеткой кластеризации, которые удовлетворяют этим условиям, называются вероятностными алгоритмами кластеризации, так как по сути степени принадлежности данных являются вероятностями, с которыми элементы принадлежат данному кластеру.
Каждый кластер
представляется своим прототипом. Поэтому проблема разделения набора данных Х,
по ![]() кластерам решается
задачей минимизации расстояний от элементов данных до центров кластеров. Это
может быть осуществлено минимизацией следующей функции
кластерам решается
задачей минимизации расстояний от элементов данных до центров кластеров. Это
может быть осуществлено минимизацией следующей функции
![]() (2.5)
(2.5)
с условиями (2.3) - (2.4), где
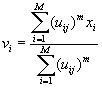 - центры кластеров.
- центры кластеров.
Параметр ![]() - экспоненциальный вес, определяющий нечеткость,
размазанность кластеров. Обычно выбирают
- экспоненциальный вес, определяющий нечеткость,
размазанность кластеров. Обычно выбирают ![]() =2.
=2.
Целевая функция ![]() обычно минимизируется
вычислением
обычно минимизируется
вычислением ![]() и
и ![]() , пока изменение
, пока изменение ![]() степеней
принадлежности не достигнет определенной точности вычисления
степеней
принадлежности не достигнет определенной точности вычисления ![]() .
.
Предложено множество
алгоритмов нечеткой кластеризации, основанных на минимизации критерия (2.5).
Нахождение матрицы нечеткого разбиения с минимальным значением критерия (2,5)
представляет собой задачу нелинейной оптимизации, которая может быть решена
разными методами. Наиболее известный и часто применяемый метод решения этой
задачи алгоритм нечетких c-средних, в основу которого положен метод
неопределенных множителей Лагранжа. Он позволяет найти локальный оптимум,
поэтому выполнение алгоритма из различных начальных точек может привести к
разным результатам.
2.1. Базовый алгоритм
нечетких с-средних
Самый простой алгоритм нечеткой кластеризации – это нечеткий алгоритм с-средних. Этот алгоритм находит компактные кластеры, например, сферической формы, которые приближены к реальным размерам и формам.
Здесь нечеткое разбиение
позволяет просто решить проблему объектов, расположенных на границе двух
кластеров - им назначают степени принадлежностей равные 0.5. Недостаток
нечеткого разбиения проявляется при работе с объектами, удаленными от центров
всех кластеров. Удаленные объекты имеют мало общего с любым из кластеров,
поэтому интуитивно хочется назначить для них малые степени принадлежности.
Однако, по условию (2.4) сумма их степеней принадлежностей такая же, как и для
объектов, близких к центрам кластеров, т.е. равна единице. Для устранения этого
недостатка можно использовать возможностное разбиение, которое требует, только
чтобы произвольный объект из ![]() принадлежал хотя бы
одному кластеру. Возможностное разбиение получается следующим ослаблением
условия (2.4):
принадлежал хотя бы
одному кластеру. Возможностное разбиение получается следующим ослаблением
условия (2.4): ![]()
Алгоритм нечетких К-средних
Шаг 1. Установить параметры
алгоритма: c - количество кластеров; m - экспоненциальный вес; ![]() - параметр останова алгоритма.
- параметр останова алгоритма.
Шаг 2. Случайным образом
сгенерировать матрицу нечеткого разбиения , удовлетворяющую условия (5) -
(6).
Шаг 3. Рассчитать центры
кластеров: ![]() .
.
Шаг 4. Рассчитать расстояния
между объектами из ![]() и центрами кластеров:
и центрами кластеров:
![]() .
.
Шаг 5. Пересчитать элементы
матрицы нечеткого разбиения (, ):
если ![]() :
: 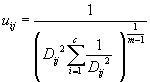 ;
;
если ![]() :
: ![]() .
.
Шаг 6. Проверить условие ![]() , где
, где ![]() - матрица нечеткого разбиения на предыдущей итерации
алгоритма. Если "да", то перейти к шагу 7, иначе - к
шагу 3.
- матрица нечеткого разбиения на предыдущей итерации
алгоритма. Если "да", то перейти к шагу 7, иначе - к
шагу 3.
Шаг 7. Конец.
В приведенном алгоритме
самым важным параметром является количество кластеров (c). Правильно выбрать
количество кластеров для реальных задач без какой-либо априорной информации о
структурах в данных достаточно сложно. Существует два формальных подхода к
выбору числа кластеров.
Первый подход основан на
критерии компактности и разделимости полученных кластеров. Логично
предположить, что при правильном выборе количества кластеров данные будут
разбиты на компактные и хорошие отделимые друг от друга группы. В противном
случае, кластеры, вероятно, не будут компактными и хорошо отделимыми.
Существует несколько критериев оценки компактности кластеров, однако вопрос о
том, как формально и достоверно определить правильность выбора количества
кластеров для произвольного набора данных все еще остается открытым. Для
алгоритма нечетких К-средних рекомендуется использовать индекс Хие-Бени:
 .
.
Второй подход предлагает
начинать кластеризацию при достаточно большом числе кластеров, а затем
последовательно объединять схожие смежные кластера. При этом используются
различные формальные критерии схожести кластеров.
Вторым параметром
алгоритма кластеризации является экспоненциальный вес (m). Чем больше m, тем
конечная матрица нечеткого разбиения ![]() становится более
"размазанной", и при
становится более
"размазанной", и при ![]() она примет вид
она примет вид ![]() , что является очень плохим решением, т. к. все объекты
принадлежат ко всем кластерам с одной и той же степенью. Кроме того,
экспоненциальный вес позволяет при формировании координат центров кластеров
усилить влияние объектов с большими значениями степеней принадлежности и уменьшить
влияние объектов с малыми значениями степеней принадлежности. На сегодня не
существует теоретически обоснованного правила выбора значения экспоненциального
веса. Обычно устанавливают
, что является очень плохим решением, т. к. все объекты
принадлежат ко всем кластерам с одной и той же степенью. Кроме того,
экспоненциальный вес позволяет при формировании координат центров кластеров
усилить влияние объектов с большими значениями степеней принадлежности и уменьшить
влияние объектов с малыми значениями степеней принадлежности. На сегодня не
существует теоретически обоснованного правила выбора значения экспоненциального
веса. Обычно устанавливают ![]() .
.
2.2.Обобщения алгоритма нечетких с-средних
В базовом
алгоритме нечетких c-средних расстояние между объектом ![]() и центром кластера
и центром кластера ![]() рассчитывается через
стандартную Евклидову норму:
рассчитывается через
стандартную Евклидову норму: ![]() . В кластерном анализе применяются и другие нормы, среди
которых часто используется диагональная норма и норма Махалонобиса.
. В кластерном анализе применяются и другие нормы, среди
которых часто используется диагональная норма и норма Махалонобиса.
В общем виде
норму можно задать через симметричную положительно определенную матрицу B
размером ![]() следующим образом:
следующим образом:
![]() ,
,
где T - операция транспонирования.
Для Евклидовой нормы
матрица B представляет собой единичную матрицу:
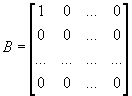 .
.
Евклидова норма
позволяет выделять кластеры в виде гиперсфер. Для диагональной нормы матрица B
задается следующим образом:
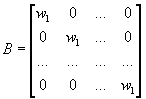 .
.
Элементы
главной диагонали матрицы интерпретируются как веса координат. Диагональная
норма позволяет выделять кластеры в виде гиперэллипсоидов, ориентированных
вдоль координатных осей.
Для нормы
Махалонобиса матрица B рассчитывается через ковариационную матрицу от ![]() :
:
![]() ,
,
где ![]() - ковариационная матрица;
- ковариационная матрица;
![]() - вектор средних значений данных.
- вектор средних значений данных.
Норма Махаланобиса
позволяет выделять кластеры в виде гиперэллипсоидов, оси которых могут быть
ориентированы в произвольных направлениях.
Примеры изолиний различных
норм, показаны на рис. 2.1. На рис. 2.2 приведен пример нечеткой
кластеризации методом нечетких c-средних при Евклидовом расстоянии. На левой
части рисунка показаны данные для кластеризации. На правой части рисунка
приведены результаты нечеткой кластеризации. Центры нечетких кластеров
обозначены символами '+'. Восемь изолиний функций принадлежности нечетких
кластеров построены для значений 0.67, 0.71, 0.75, 0.79, 0.83, 0.87, 0.91 и
0.95.
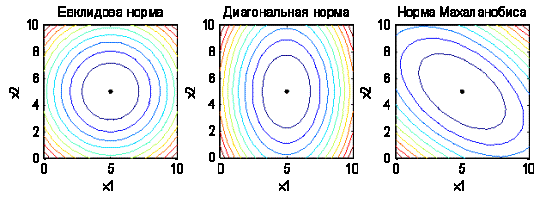
Рисунок 2.1
- Изолинии различных норм
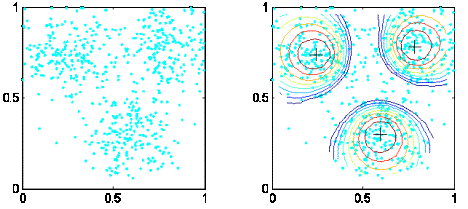
Рисунок 2.2 - Нечеткая
кластеризация при Евклидовой норме
Для некоторых наборов
данных "глазная кластеризация" позволяет выделить скопления данных в
виде различных геометрических фигур: сферы, эллипсоиды разной ориентации,
цепочки и т.п. В результате алгоритмов кластеризации с фиксированной нормой
форма всех кластеров получается одинаковой. Алгоритмы кластеризации как бы
навязывают данным неприсущую им структуру, что приводит не только к
неоптимальным, но иногда и к принципиально неправильным результатам, Для
устранения этого недостатка предложено несколько методов, среди которых выделим
алгоритм Густафсона-Кесселя (Gustafson-Kessel algorithm).
2.3.Алгоритм Густафсона-Кесселя
Алгоритм Густафсона-Кесселя
использует адаптивную норму для каждого кластера, т.е. для каждого i-го кластера
существует своя норм-порождающая матрица ![]() . В этом алгоритме при кластеризации оптимизируются не только
координаты центров кластеров и матрица нечеткого разбиения, но также и
норм-порождающие матрицы для всех кластеров. Это позволяет выделять кластера
различной геометрической формы. Критерий оптимальности (2.5) линеен
относительно
. В этом алгоритме при кластеризации оптимизируются не только
координаты центров кластеров и матрица нечеткого разбиения, но также и
норм-порождающие матрицы для всех кластеров. Это позволяет выделять кластера
различной геометрической формы. Критерий оптимальности (2.5) линеен
относительно ![]() , поэтому для получения ненулевых решений, вводят некоторые
ограничения на норм-пораждающие матрицы. В алгоритме Густафсона-Кесселя это
ограничение на значение определителя норм-пораждающих матриц:
, поэтому для получения ненулевых решений, вводят некоторые
ограничения на норм-пораждающие матрицы. В алгоритме Густафсона-Кесселя это
ограничение на значение определителя норм-пораждающих матриц:
![]() ,
, ![]() ,
,![]() .
.
Оптимальное решение
находится посредством метода неопределенных множителей Лагранжа.
Вывод:
Преимущества: алгоритм Густафсона-Кесселя находит кластеры в виде гиперэллипсоидов различной ориентации, в отличии от алгоритма с-средних, который находит кластеры одинаковой (сферической ) формы. Также алгоритм Густафсона-Кесселя может применяться для поиска линейных кластеров. Это возможно, так как линии и плоскости могут быть представлены как вырожденные эллипсы или эллипсоиды.
Недостатки: алгоритм Густафсона-Кесселя, по сравнению с алгоритмом нечетких c-средних, обладает значительно большей вычислительной трудоемкостью.
В сочетании с алгоритмом
К-средних, этот алгоритм часто используется для инициализации других алгоритмов
нечеткой кластеризации.
2.4. Синтез нечетких правил по результатам нечеткой
кластеризации
Нечеткие правила можно синтезировать по результатам
нечеткой кластеризации. Пусть объекты кластеризации имеют два признака (![]() ).Тогда результаты нечеткого разбиения можно представить
трехмерным графиком: для каждого объекта отложить по осям абсцисс и ординат
значения признаков, а по оси аппликат - степень принадлежности объекта
нечеткому кластеру. Количество таких графиков будет равно числу кластеров (n).
).Тогда результаты нечеткого разбиения можно представить
трехмерным графиком: для каждого объекта отложить по осям абсцисс и ординат
значения признаков, а по оси аппликат - степень принадлежности объекта
нечеткому кластеру. Количество таких графиков будет равно числу кластеров (n).
Пример А. Данные представлены
следующей таблицей:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
x1 |
1 |
1 |
1 |
3 |
3 |
3 |
5 |
7 |
9 |
11 |
11 |
11 |
13 |
13 |
13 |
|
x2 |
1 |
4 |
7 |
2 |
4 |
6 |
4 |
4 |
4 |
2 |
4 |
6 |
1 |
4 |
7 |
Графическое изображение
этих данных представляет собой "бабочку" ‑ хорошо
известный в теории распознавания образов пример кластеризации. Установим такие
параметры алгоритма нечетких c-средних: c=2, m=2 и ![]() . После 8-ми итераций получаем следующее нечеткое разбиение:
. После 8-ми итераций получаем следующее нечеткое разбиение:
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
0.909 |
0.976 |
0.909 |
0.947 |
0.998 |
0.947 |
0.879 |
0.5 |
0.121 |
0.053 |
0.002 |
0.053 |
0.091 |
0.024 |
0.0911 |
|
|
0.091 |
0.024 |
0.091 |
0.053 |
0.002 |
0.053 |
0.121 |
0.5 |
0.879 |
0.947 |
0.998 |
0.947 |
0.909 |
0.976 |
0.909 |
Значение критерия (2.5)
для этого нечеткого разбиения равно 82.94. Трехмерные изображения нечетких
кластеров приведены на рис. 2.3.
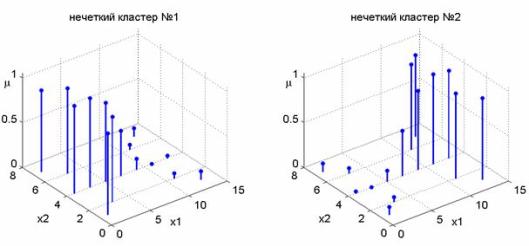
Рисунок 2.3 -
Нечеткие кластера из примера А
Функции принадлежности нечетких кластеров
(рис. 2.3) напоминают нечеткие отношения. Следовательно, каждому кластеру
можно поставить в соответствие одно нечеткое правило. По результатам нечеткой
кластеризации можно синтезировать нечеткие правила различных баз знаний:
синглтоной, Мамдани и Сугено. Функции принадлежности термов в посылках правила
получаются проецированием степеней принадлежности соответствующего кластера
(строчки матрицы нечеткого разбиения ![]() ) на входные переменные. Затем полученные множества степеней
принадлежностей аппроксимируют подходящими параметрическими функциями
принадлежности.
) на входные переменные. Затем полученные множества степеней
принадлежностей аппроксимируют подходящими параметрическими функциями
принадлежности.
В качестве заключения правила синглтоной базы
знаний выбирают координату центра кластера. Заключения правил базы знаний
Мамдани находят также как и функции принадлежности термов входных переменных.
Заключения правил базы знаний Сугено находят по методу наименьших квадратов.
При кластеризации с использованием нормы Махалонобиса в качестве заключений
правил типа Сугено могут быть выбраны уравнения длинных осей гиперэллипсоидов.
Пример Б. Данные для кластеризации
изображены на рис. 2.4. На этом рисунке также показаны центры двух
нечетких кластеров и изолинии для следующих значений функций принадлежности
нечетким кластерам: 0.95, 0.9, 0.85, 0.8, 075, 0.7 и 0.65. Функции
принадлежности нечетких кластеров также изображены двумя трехмерными
поверхностями. Они интерпретируются следующими нечеткими правилами:
Если x=низкий, то
y=низкий,
Если x= высокий, то
y=высокий,
с функциями принадлежности
термов, показанными на рис. 2.5. Функции принадлежности получены
проецированием поверхностей с рис. Б на переменные x и y. Маркеры на
графиках функций принадлежности соответствует одному объекту кластеризации.
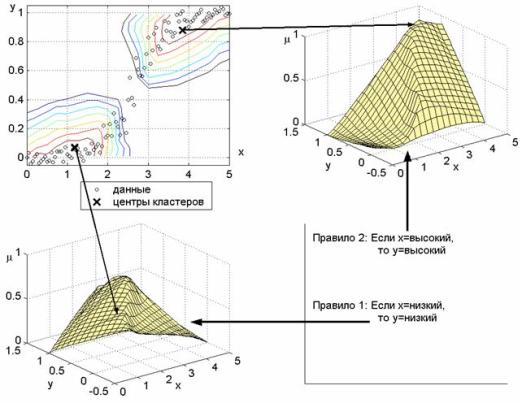
Рисунок 2.4 - К
примеру Б: экстракция нечетких правил через нечеткую кластеризацию
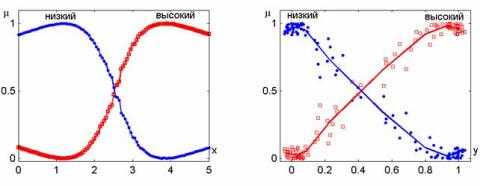
Рисунок 2.5 - К
примеру Б: функции принадлежности
3 Кластеризация без
задания количества кластеров
Метод горной кластеризации не требует задания количества
кластеров. Метод предложен Р. Ягером и Д. Филевым в 1993 г.
Кластеризация по горному методу не является нечеткой, однако, ее часто
используют при синтезе нечетких правил из данных. Применение горной
кластеризации при проектировании нечетких баз знаний описывается в конце
параграфа.
3.1. Основные идеи метода горной кластеризации
На первом шаге горной кластеризации определяют точки,
которые могут быть центрами кластеров. На втором шаге для каждой такой точки
рассчитывается значение потенциала, показывающего возможность формирования
кластера в ее окрестности. Чем плотнее расположены объекты в окрестности потенциального
центра кластера, тем выше значение его потенциала. После этого итерационно
выбираются центры кластеров среди точек с максимальными потенциалами.
На первом шаге необходимо сформировать потенциальные центры
кластеров. Для алгоритма горной кластеризации число потенциальных центров
кластеров (Q) должно быть конечным. Ими могут быть объекты кластеризации
(строчки матрицы ![]() ),
тогда
),
тогда ![]() .
Второй способ выбора потенциальных центров кластеров состоит в дискретизации
пространство входных признаков. Для этого диапазоны изменения входных признаков
разбивают на несколько интервалов. Проводя через точки разбиения прямые,
параллельные координатным осям, получаем "решеточный" гиперкуб. Узлы
этой решетки и будут соответствовать центрам потенциальных кластеров. Обозначим
через
.
Второй способ выбора потенциальных центров кластеров состоит в дискретизации
пространство входных признаков. Для этого диапазоны изменения входных признаков
разбивают на несколько интервалов. Проводя через точки разбиения прямые,
параллельные координатным осям, получаем "решеточный" гиперкуб. Узлы
этой решетки и будут соответствовать центрам потенциальных кластеров. Обозначим
через ![]() - количество значений, которые могут принимать центры кластеров по
- количество значений, которые могут принимать центры кластеров по ![]() -й
координате (
-й
координате (![]() ).
Тогда количество возможных кластеров будет равно:
).
Тогда количество возможных кластеров будет равно: ![]() .
.
На втором шаге алгоритма рассчитывается
потенциал центров кластеров по следующей формуле:
![]() ,
,
![]() ,
,
где ![]() - потенциальный центр h-го кластера;
- потенциальный центр h-го кластера;
![]() - положительная константа
- положительная константа
![]() - расстояние между потенциальным центром кластера (
- расстояние между потенциальным центром кластера (![]() )
и объектом кластеризации (
)
и объектом кластеризации (![]() ).
В евклидовом пространстве это расстояние рассчитывается по формуле:
).
В евклидовом пространстве это расстояние рассчитывается по формуле:
![]() .
.
В случае, когда объекты
кластеризации заданы двумя признаками (n=2), графическое
изображение распределения потенциала будет представлять собой поверхность,
напоминающую горный рельеф. Отсюда и название - горный метод
кластеризации.
На третьем шаге алгоритма в качестве
центров кластеров выбирают координаты "горных" вершин. Для этого,
центром первого кластера назначают точку с наибольшим потенциалом. Обычно,
наивысшая вершина окружена несколькими достаточно высокими пиками. Поэтому
назначение центром следующего кластера точки с максимальным потенциалом среди
оставшихся вершин привело бы к выделению большого числа близко расположенных
центров кластеров. Чтобы выбрать следующий центр кластера необходимо вначале
исключить влияние только что найденного кластера. Для этого значения потенциала
для оставшихся возможных центров кластеров пересчитывается следующим образом:
от текущих значений потенциала вычитают вклад центра только что найденного
кластера (поэтому кластеризацию по этому методу иногда называют субтрактивной).
Перерасчет потенциала происходит по формуле:
![]() ,
,
где ![]() - потенциал на 1-й итерации;
- потенциал на 1-й итерации;
![]() - потенциал на 2-й итерации;
- потенциал на 2-й итерации;
![]() - центр первого найденного кластера:
- центр первого найденного кластера: ![]() ;
;
![]() - положительная константа.
- положительная константа.
Центр второго кластера
определяется по максимальному значению обновленного потенциала:
![]() .
.
Затем снова
пересчитывается значение потенциалов:
![]() .
.
Итерационная процедура
пересчета потенциалов и выделения центров кластеров продолжается до тех пор,
пока максимальное значение потенциала превышает некоторый порог.
3.2. Синтез нечеткой базы знаний на основе горной
кластеризации
Обозначим через ![]() - центры кластеров, найденные в результате горной кластеризации. Для упрощения
выкладок примем, что центры кластеров заданы двумя координатами:
- центры кластеров, найденные в результате горной кластеризации. Для упрощения
выкладок примем, что центры кластеров заданы двумя координатами: ![]() ,
,
![]() .
Задача состоит в синтезе нечетких правил, связывающих вход (x) с выходом (y).
.
Задача состоит в синтезе нечетких правил, связывающих вход (x) с выходом (y).
Центру кластера ![]() (
(![]() )
ставится в соответствие одно нечеткое правило:
)
ставится в соответствие одно нечеткое правило:
Если ![]() ,
то
,
то ![]() ,
,
в котором нечеткие термы
интерпретируются так: ![]() -
- ![]() и
и
![]() -
- ![]() .
Функции принадлежностей этих нечетких термов задаются гауссовской кривой:
.
Функции принадлежностей этих нечетких термов задаются гауссовской кривой:
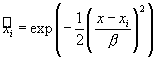 ,
,
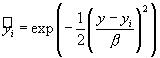 ,
,
где ![]() - параметр алгоритма горной кластеризации.
- параметр алгоритма горной кластеризации.
Заключение
Итак, рассмотрели математические основы нечеткой кластеризации, основные алгоритмы с предварительным заданием количества кластеров и без него. Среди первых выделили алгоритм с-средних и его модификацию – алгоритм Густафсона-Кесселя. При этом значительным преимуществом обладает второй алгоритм, так как находит кластеры различной формы, но является более трудоемким в вычислительном плане. Показаны примеры синтеза нечетких правил по результатам нечеткой кластеризации.
Описаны
основные идеи горной кластеризации, при которой не требуется такие априорные
данные, как количество кластеров. Этот алгоритм не является нечетким, но
используется при синтезе нечетких правил для данных. Подробно рассмотрен
алгоритм горной кластеризации