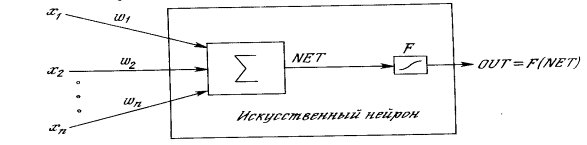
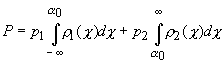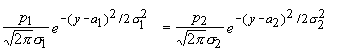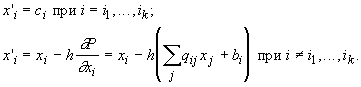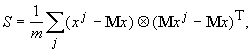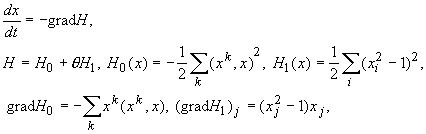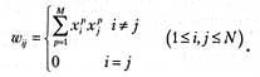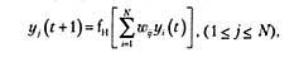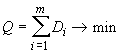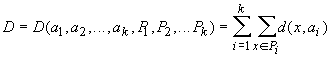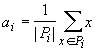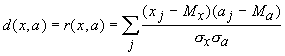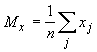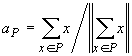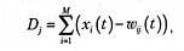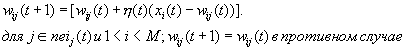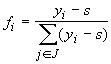Использование нейронных сетей в Data Mining

СОДЕРЖАНИЕ

Введение  3

Глава 1.Классификация задач Data Mining   5

Глава 2.Модели Data Mining   7

Глава 3.Нейронные сети как метод добычи знаний  9

3.1.Элементы нейронных сетей   10

3.2.Активационные функции   11

3.3.Архитектуры нейронных сетей   13

Глава 4.Решение задач нейронными сетями  14

4.1.Задача четкого разделения двух классов  14

4.1.1.Математический аппарат  14

4.1.2.ПЕРСЕПТРОН Розенблатта. 17

4.1.2.1.Алгоритм обучения персептрона. 18

4.1.3.Алгоритм построения гиперплоскости, разделяющей классы. 18

4.2.Заполнение пробелов в данных (прогнозирование значений)  19

4.2.1.Математический аппарат. 19

4.2.2.Сети Хопфилда  21

4.2.2.1.Топология, обучение и алгоритм действий сети  23

4.2.3.Анализ баз данных с помощью нейронной сети Хопфилда  24

4.2.3.1.Этапы работы при анализе базы данных с использованием нейронной сети. 27

4.3.Сети Кохонена для кластер-анализа и классификации без учителя. 28

4.3.1.Математический аппарат  28

4.3.2.Сети Кохонена. Топология, обучение и алгоритм действий сети. 32

4.3.3.Различные способы использования полученных классификаторов. 34

4.3.4.Общий подход к построению классификатора на основе нейронных сетей. 35

Заключение  37

Список использованных источников. 38

 

 

 

Введение

            Основной задачей аналитика является генерация гипотез. Он решает ее, основываясь на своих знаниях и опыте. Однако знания есть не только у человека, но и в накопленных данных, которые подвергаются анализу. Такие знания часто называют "скрытыми", т.к. они содержатся в гигабайтах и терабайтах информации, которые человек не в состоянии исследовать самостоятельно, В связи с этим существует высокая вероятность пропустить гипотезы, которые могут принести значительную выгоду.

            Очевидно, что для обнаружения скрытых знаний необходимо применять специальные методы автоматического анализа, при помощи которых приходится практически добывать знания из "завалов" информации. За этим направлением прочно закрепился термин добыча данных или Data Mining. Классическое определение этого термина дал в 1996 г. один из основателей этого направления Пятецкий-Шапиро.

            Data Mining - исследование и обнаружение "машиной" (алгоритмами, средствами искусственного интеллекта) в сырых данных скрытых знаний, которые ранее не были известны, нетривиальны, практически полезны, доступны для интерпретации человеком.

 

            В Data Mining для представления полученных знаний служат модели. Виды моделей зависят от методов их создания. Наиболее распространенными являются: правила, деревья решений, кластеры и математические функции. Данная работа посвящена отдельному классу моделей, основанных на биологической аналогии с мозгом человека и предназначенных после прохождения этапа обучения на имеющихся данных для решения разнообразных задач анализа данных – технологии нейронных сетей.

Глава 1.Классификация задач Data Mining

            Методы Data Mining помогают решить многие задачи, с которыми сталкивается аналитик. Из них основными являются: классификация, регрессия, поиск ассоциативных правил и кластеризация. Ниже приведено краткое описание основных задач анализа данных.

·       Задача классификации сводится к определению класса объекта по его характеристикам. Необходимо заметить, что в этой задаче множество классов, к которым может быть отнесен объект, заранее известно.

·       Задача регрессии, подобно задаче классификации, позволяет определить по известным характеристикам объекта значение некоторого его параметра. В отличие от задачи классификации значением параметра является не конечное множество классов, а множество действительных чисел.

·       При поиске ассоциативных правил целью является нахождение частых зависимостей (или ассоциаций) между объектами или событиями. Найденные зависимости представляются в виде правил и могут быть использованы как для лучшего понимания природы анализируемых данных, так и для предсказания появления событий.

·       Задача кластеризации заключается в поиске независимых групп (кластеров) и их характеристик во всем множестве анализируемых данных. Решение этой задачи помогает лучше понять данные. Кроме того, группировка однородных объектов позволяет сократить их число, а следовательно, и облегчить анализ.

            Перечисленные задачи по назначению делятся на описательные и предсказательные.

            Описательные (descriptive) задачи уделяют внимание улучшению понимания анализируемых данных. Ключевой момент в таких моделях — легкость и прозрачность результатов для восприятия человеком. Возможно, обнаруженные закономерности будут специфической чертой именно конкретных исследуемых данных и больше нигде не встретятся, но это все равно может быть полезно и потому должно быть известно. К такому виду задач относятся кластеризация и поиск ассоциативных правил.

            Решение предсказательных (predictive) задач разбивается на два этапа. На

первом этапе на основании набора данных с известными результатами строится модель. На втором этапе она используется для предсказания результатов на основании новых наборов данных. При этом, естественно, требуется, чтобы построенные модели работали максимально точно. К данному виду задач относят задачи классификации и регрессии. Сюда можно отнести и задачу поиска ассоциативных правил, если результаты ее решения могут быть использованы для предсказания появления некоторых событий.

            По способам решения задачи разделяют на supervised learning (обучение с учителем) и unsupervised learning (обучение без учителя).В случае supervised learning задача анализа данных решается в несколько этапов. Сначала с помощью какого-либо алгоритма Data Mining строится модель анализируемых данных - классификатор. Затем классификатор подвергается обучению. Другими словами, проверяется качество его работы и, если оно не удовлетворительно, происходит дополнительное обучение классификатора. Так продолжается до тех пор, пока не будет достигнут требуемый уровень качества или не станет ясно, что выбранный алгоритм не работает корректно данными, либо же сами данные не имеют структуры, которую можно выявить. К этому типу задач относят задачи классификации и регрессии.

            Unsupervised learning объединяет задачи, выявляющие описательные модели, например закономерности в покупках, совершаемых клиентами большого магазина. Очевидно, что если эти закономерности есть, то модель должна их представить и неуместно говорить об ее обучении. Отсюда и название - unsupervised learning. Достоинством таких задач является возможность их решения без каких-либо предварительных знаний об анализируемых данных. К ним относятся задачи кластеризации и поиска ассоциативных правил.

Глава 2.Модели Data Mining

            Цель технологии Data Mining – нахождение в данных таких моделей, которые не могут быть найдены обычными методами. Существуют два вида моделей: предсказательные и описательные.

            Предсказательные(predictive) модели.

            Предсказательные модели строятся на основании выбора данных с известными результатами. Они используются для предсказания результатов на основании других наборов данных. При этом, естественно, требуется, чтобы модель работала максимально точно, была статистически значима и оправданна и т.д.

К ним относятся следующие модели:

·       классификации — описывают правила или набор правил, в соответствии с которыми можно отнести описание любого нового объекта к одному из классов. Такие правила строятся на основании информации о существующих объектах путем разбиения их на классы;

·       последовательностей — описывают функции, позволяющие прогнозировать изменение непрерывных числовых параметров. Они строятся на основании данных об изменении некоторого параметра за прошедший период времени.

 

            Описательные (descriptive) модели

            Описательные модели уделяют внимание сути зависимостей в наборе данных взаимному влиянию различных факторов, т.е. на построении эмпирических моделей различных систем. Ключевой момент в таких моделях— легкость и прозрачность для восприятия человеком. Возможно, обнаруженные закономерности будут специфической чертой именно конкретных исследуемых данных и больше нигде не встретятся, но это все равно может быть полезно и потому должно быть известно.

            К ним относятся следующие виды моделей:

·       регрессионные — описывают функциональные зависимости между зависимыми и независимыми показателями и переменными в понятной человеку форме. Необходимо заметить, что такие модели описывают функциональную зависимость не только между непрерывными числовыми параметрами, но и между категориальными;

·       кластеризации — описывают группы (кластеры), на которые можно разде­лить объекты, данные о которых подвергаются анализу. Группируются объекты (наблюдения, события) на основе данных (свойств), описывающих сущность объектов. Объекты внутри кластера должны быть "похожими" друг на друга и отличаться от объектов, вошедших в другие кластеры. Чем больше похожи объекты внутри кластера и чем больше отличий между кластерами, тем точнее кластеризация;

·       исключений – описывают исключительные ситуации в записях (например, отдельных пациентов), которые резко отличаются чем-либо от основного множества записей (группы больных). Знание исключений может быть использовано двояким образом. Возможно, что эти записи представляют собой случайный сбой, например ошибки операторов, вводивших данные в компьютер. С другой стороны, отдельные, исключительные записи могут представлять самостоятельный интерес для исследования, т. к. они могут указывать на некоторые редкие, но важные аномальные заболевания. Даже сама идентификация этих записей, не говоря об их последующем анализе и детальном рассмотрении, может оказаться очень полезной для понимания сущности изучаемых объектов или явлений;

·       итоговые – выявление ограничений на данные анализируемого массива. Например, при изучении выборки данных по пациентам не старше 30 лет, перенесшим инфаркт миокарда, обнаруживается, что все пациенты, описанные в этой выборке, либо курят более 5 пачек сигарет в день, либо имеют вес не ниже 95 кг. Подобные ограничения важны для понимания данных массива; по сути дела — это новое знание, извлеченное в результате анализа. Таким образом, Data Summarization — это нахождение каких-либо фактов, которые верны для всех или почти всех записей в изучаемой выборке данных, но которые достаточно редко встречались бы во всем мыслимом многообразии записей такого же формата и, например. характеризовались бы теми же распределениями значений полей.;

·       ассоциации — выявление закономерностей между связанными событиями. Примером такой закономерности служит правило, указывающее, что из события Х следует событие У. Такие правила называются ассоциативными.

 

            Для построения рассмотренных моделей используются различные методы и алгоритмы Data Mining. Ввиду того, что технология Data Mining развивалась и развивается на стыке таких дисциплин, как статистика, теория информации, машинное обучение, теория баз данных, вполне закономерно, что большинство алгоритмов и методов Data Mining были разработаны на основе различных технологий и концепций. Одной из технологий, часто реализуемой методами Data Mining , является технология нейронных сетей.

Глава 3.Нейронные сети как метод добычи знаний

            Нейронные сети — это класс моделей, основанных на биологической аналогии с мозгом человека и предназначенных после прохождения этапа так называемого обучения на имеющихся данных для решения разнообразных задач анализа данных. При применении этих методов прежде всего встает вопрос выбора конкретной архитектуры сети (числа "слоев" и количества "нейронов" в каждом из них). Размер и структура сети должны соответствовать (например, в смысле формальной вычислительной сложности) существу исследуемого явления. Поскольку на начальном этапе анализа природа явления обычно известна плохо, выбор архитектуры является непростой задачей и часто связан с длительным процессом "проб и ошибок" (однако в последнее время стали появляться нейронно-сетевые программы, в которых для решения трудоемкой задачи поиска наилучшей архитектуры сети применяются методы искусственного интеллекта).

            Затем построенная сеть подвергается процессу так называемого обучения. На этом этапе нейроны сети итеративно обрабатывают входные данные и корректируют свои веса так, чтобы сеть наилучшим образом прогнозировала (в традиционных терминах следовало бы сказать "осуществляла подгонку") данные, на которых выполняется "обучение". После обучения на имеющихся данных сеть готова к работе и может использоваться для построения прогнозов.

            Нейронная сеть, полученная в результате "обучения", выражает закономерности, присутствующие в данных. При таком подходе она оказывается функциональным эквивалентом некоторой модели зависимостей между переменными, подобной тем, которые строятся в традиционном моделировании. Однако, в отличие от традиционных моделей, в случае нейронных сетей эти зависимости не могут быть записаны в явном виде, подобно тому как это делается в статистике (например, "А положительно коррелированно с В для наблюдений, у которых величина С мала, а D велика"). Иногда нейронные сети выдают прогноз очень высокого качества; однако они представляют собой типичный пример нетеоретического подхода к исследованию (иногда это называют "черным ящиком"). При таком подходе сосредотачиваются исключительно на практическом результате, в данном случае на точности прогнозов и их прикладной ценности, а не на сути механизмов, лежащих в основе явления .или соответствии полученных результатов какой-либо имеющейся теории.

            Следует, однако, отметить, что методы нейронных сетей могут применяться и в исследованиях, направленных на построение объясняющей модели явления, поскольку нейронные сети помогают изучать данные с целью поиска значимых переменных или групп таких переменных, и полученные результаты могут облегчить процесс последующего построения модели. Более того, сейчас имеются нейросетевые программы, которые с помощью сложных алгоритмов могут находить наиболее важные входные переменные, что уже непосредственно помогает строить модель.

            Одно из главных преимуществ нейронных сетей состоит в том, что они, по крайней мере теоретически, могут аппроксимировать любую непрерывную функцию, и поэтому исследователю нет необходимости заранее принимать какие-либо гипотезы относительно модели и даже, в ряде случаев, о том, какие переменные действительно важны. Однако существенным недостатком нейронных сетей является то обстоятельство, что окончательное решение зависит от начальных установок сети и, как уже отмечалось, его практически невозможно интерпретировать в традиционных аналитических терминах, которые обычно применяются при построении теории явления.

3.1.Элементы нейронных сетей

            Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис.3.1.1 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x1, x2,…, xn, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w1, w2,…, wn, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом:

NET = XW.

Рис.3.1.1. Искусственный нейрон

3.2.Активационные функции

            Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией

OUT = K(NET),

где К – постоянная, пороговой функции

OUT =1,если NET > T,

OUT = 0 в остальных случаях,

где Т – некоторая постоянная пороговая величина, или же функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.

Рис.3.2.1.Искусственный нейрон с активационной функцией

            На рис.3.2.1 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция, показанная на рис.3.2.2. Эта функция математически выражается как F(x) = 1/(1 + е-x). Таким образом,

.

Рис.3.2.2. Сигмоидальная логистическая функция

3.3.Архитектуры нейронных сетей

            Во всем многообразии искусственных нейронных сетей можно выделить две базовые архитектуры - слоистые и полносвязные сети.

            Слоистые сети : нейроны расположены в несколько слоев. Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее срабатывает второй слой и т.д. до k -го слоя, который выдает выходные сигналы. Если не оговорено противное, то каждый выходной сигнал i -го слоя подается на вход всех нейронов i +1-го. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал.

            Полносвязные сети: каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам.

Рис.3.3.1. Архитектуры нейронных сетей.

            Элементы слоистых и полносвязных сетей могут выбираться по-разному. Существует, впрочем, стандартный выбор - нейрон с неоднородным адаптивным линейным сумматором на входе (рис.3.3.1).

Глава 4.Решение задач нейронными сетями

            В данной главе описано несколько базовых задач Data Mining для решения нейронными сетями и основные или исторически первые (авторские) методы настройки сетей для их решения; представлена топология используемых сетей и алгоритмы решения некоторых практических задач. К базовым задачам Data Mining, решаемым нейронными сетями, можно отнести следующие:

 

1.   Классификация и кластеризация (с учителем) (персептрон Розенблатта).

2.   Восстановление пробелов в данных (сети Хопфилда).

3.   Кластер-анализ и классификация (без учителя) (сети Кохонена).

4.1.Задача четкого разделения двух классов

4.1.1.Математический аппарат

            Задача четкого разделения двух классов по обучающей выборке ставится так: имеется два набора векторов x1 , ..., xm и y1,...,ym . Заранее известно, что xi относится к первому классу, а yi - ко второму. Требуется построить решающее правило, то есть определить такую функцию f(x), что при f(x)>0 вектор x относится к первому классу, а при f(x)<0 ‑ ко второму.

            Координаты классифицируемых векторов представляют собой значения некоторых признаков (свойств) исследуемых объектов. Эта задача возникает во многих случаях: при диагностике болезней и определении неисправностей машин по косвенным признакам, при распознавании изображений и сигналов и т.п.

            Строго говоря, классифицируются не векторы свойств, а объекты, которые обладают этими свойствами. Это замечание становится важным в тех случаях, когда возникают затруднения с построением решающего правила – например, тогда, когда встречаются принадлежащие к разным классам объекты, имеющие одинаковые признаки. В этих случаях возможно несколько решений:

1)     искать дополнительные признаки, позволяющие разделить классы;

2)     примириться с неизбежностью ошибок, назначить за каждый тип ошибок свой штраф (c12 - штраф за то, что объект первого класса отнесен ко второму, c21 - за то, что объект второго класса отнесен к первому) и строить разделяющее правило так, чтобы минимизировать математическое ожидание штрафа;

3)     перейти к нечеткому разделению классов - строить так называемые "функции принадлежности" f1(x) и f2(x) ‑ fi(x) оценивает степень уверенности при отнесении объекта к i-му классу (i=1,2), для одного и того же x может быть так, что и f1(x)>0, и f2(x)>0.

            Линейное разделение классов состоит в построении линейного решающего правила ‑ то есть такого вектора a и числа a0 (называемого порогом), что при (x,a)>a0 x относится к первому классу, а при (x, a)<a0 - ко второму.

            Поиск такого решающего правила можно рассматривать как разделение классов в проекции на прямую. Вектор a задает прямую, на которую ортогонально проектируются все точки, а число a0 ‑ точку на этой прямой, отделяющую первый класс от второго.

            Простейший и подчас очень удобный выбор состоит в проектировании на прямую, соединяющую центры масс выборок. Центр масс вычисляется в предположении, что массы всех точек одинаковы и равны 1. Это соответствует заданию a в виде

a= (y1+ y2+...+ym)/m ‑(x1+ x2+...+ x n)/n.

            Во многих случаях удобнее иметь дело с векторами единичной длины. Нормируя a, получаем:

a= ((y1+ y2+...+ym)/m ‑(x1+ x2+...+ x n)/n)/||(y1+ y2+...+ym)/m ‑(x1+ x2+...+ x n)/n||.

            Выбор a0 может производиться из различных соображений. Простейший вариант ‑ посередине между центрами масс выборок:

a0=(((y1+ y2+...+ym)/m,a)+((x1+ x2+...+ x n)/n,a))/2.

            Более тонкие способы построения границы раздела классов a0 учитывают различные вероятности появления объектов разных классов, и оценки плотности распределения точек классов на прямой. Чем меньше вероятность появления данного класса, тем более граница раздела приближается к центру тяжести соответствующей выборки.

            Можно для каждого класса построить приближенную плотность вероятностей распределения проекций его точек на прямую (это намного проще, чем для многомерного распределения) и выбирать a0, минимизируя вероятность ошибки. Пусть решающее правило имеет вид: при (x, a)>a0 x относится к первому классу, а при (x, a)<a0 ‑ ко второму. В таком случае вероятность ошибки будет равна

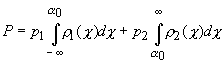
где p1, p2 ‑ априорные вероятности принадлежности объекта соответствующему классу,

r1(c), r2(c) ‑ плотности вероятности для распределения проекций c точек x в каждом классе.

            Приравняв нулю производную вероятности ошибки по a0, получим: число a0, доставляющее минимум вероятности ошибки, является корнем уравнения:

p1r1(c)=p2r2(c),                                                       (7)

либо (если у этого уравнения нет решений) оптимальным является правило, относящее все объекты к одному из классов.

            Если принять гипотезу о нормальности распределений:

,

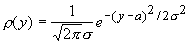то для определения a0 получим:

,

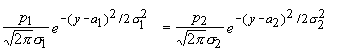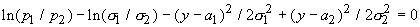
            Если это уравнение имеет два корня y=a1, a2, (a1<a2) то наилучшим решающим правилом будет: при a1<(x, a)<a2 объект принадлежит одному классу, а при a1>(x, a) или (x, a)>a2 ‑ другому (какому именно, определяется тем, которое из произведений piri(c) больше). Если корней нет, то оптимальным является отнесение к одному из классов. Случай единственного корня представляет интерес только тогда, когда s1=s2. При этом уравнение превращается в линейное и мы приходим к исходному варианту ‑ единственной разделяющей точке a0.

            Таким образом, разделяющее правило с единственной разделяющей точкой a0 не является наилучшим для нормальных распределений и надо искать две разделяющие точки.

            Если сразу ставить задачу об оптимальном разделении многомерных нормальных распределений, то получим, что наилучшей разделяющей поверхностью является квадрика (на прямой типичная «квадрика» ‑ две точки). Предполагая, что ковариационные матрицы классов совпадают (в одномерном случае это предположение о том, что s1=s2), получаем линейную разделяющую поверхность. Она ортогональна прямой, соединяющей центры выборок не в обычном скалярном произведении, а в специальном: 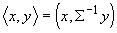, где S ‑ общая ковариационная матрица классов.

            Важная возможность усовершенствовать разделяющее правило состоит с использовании оценки не просто вероятности ошибки, а среднего риска: каждой ошибке приписывается «цена» ci и минимизируется сумма c1p1r1(c)+c2p2r2(c). Ответ получается практически тем же (всюду pi заменяются на cipi), но такая добавка важна для многих приложений.

            Требование безошибочности разделяющего правила на обучающей выборке принципиально отличается от обсуждавшихся критериев оптимальности. На основе этого требования строится персептрон Розенблатта ‑ «дедушка» современных нейронных сетей.

4.1.2.ПЕРСЕПТРОН Розенблатта.

            Одной из первых искусственных сетей, способных к перцепции (восприятию) и формированию реакции на воспринятый стимул, явился PERCEPTRON Розенблатта (F.Rosenblatt, 1957).

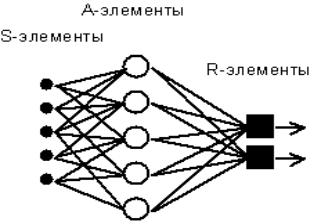
Рис. 4.1.2.1. Элементарный персептрон Розенблатта.

            Простейший классический персептрон содержит нейроподобные элементы трех типов (см. Рис. 4.1.2.1). S-элементы формируют сетчатку сенсорных клеток, принимающих двоичные сигналы от внешнего мира. Далее сигналы поступают в слой ассоциативных или A-элементов. Только ассоциативные элементы, представляющие собой формальные нейроны, выполняют нелинейную обработку информации и имеют изменяемые веса связей. R-элементы с фиксированными весами формируют сигнал реакции персептрона на входной стимул.

            Представленная на рисунке сеть является однослойной, так как имеет только один слой нейропроцессорных элементов. Однослойный персептрон характеризуется матрицей синаптических связей W от S- к A-элементам. Элемент матрицы 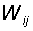отвечает связи, ведущей от i-го S-элемента к j-му A-элементу.

            С сегодняшних позиций однослойный персептрон представляет лишь исторический интерес.

4.1.2.1.Алгоритм обучения персептрона.

            Обучение сети состоит в подстройке весовых коэффициентов каждого нейрона. Пусть имеется набор пар векторов (xa, ya), a = 1..p, называемый обучающей выборкой. Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на входы сети каждого вектора xa на выходах всякий раз получается соответсвующий вектор ya

            Предложенный Ф.Розенблаттом метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает несколько шагов:

1.     Начальные значения весов всех нейронов 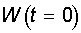полагаются случайными.

2.     Сети предъявляется входной образ xa, в результате формируется выходной образ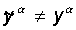

3.     Вычисляется вектор ошибки 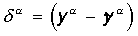, делаемой сетью на выходе. Дальнейшая идея состоит в том, что изменение вектора весовых коэффициентов в области малых ошибок должно быть пропорционально ошибке на выходе, и равно нулю если ошибка равна нулю.

4.     Вектор весов модифицируется по следующей формуле: 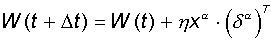. Здесь 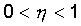- темп обучения.

5.     Шаги 1-3 повторяются для всех обучающих векторов. Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, а) когда итерации сойдутся, т.е. вектор весов перестает изменяться, или б) когда полная просуммированная по всем векторам абсолютная ошибка станет меньше некоторого малого значения.

            Представленный алгоритм относится к широкому классу алгоритмов обучения с учителем, поскольку известны как входные вектора, так и требуемые значения выходных векторов (имеется учитель, способный оценить правильность ответа ученика).

4.1.3.Алгоритм построения гиперплоскости, разделяющей классы.

            Возьмем за основу при построении гиперплоскости, разделяющей классы, отсутствие ошибок на обучающей выборке. Чтобы удовлетворить этому условию, придется решать систему линейных неравенств:

(xi, a)>a0 (i=1,...,n)

(yj , a)<a0 (j=1,...,m).

            Здесь xi (i=1,..,n) - векторы из обучающей выборки, относящиеся к первому классу, а yj (j=1,..,n) - ко второму.

            Удобно переформулировать задачу. Увеличим размерности всех векторов на единицу, добавив еще одну координату ‑a0 к a, x0 =1 - ко всем x и y0 =1 ‑ ко всем y . Сохраним для новых векторов прежние обозначения - это не приведет к путанице.

Наконец, положим zi =xi (i=1,...,n), zj = ‑yj (j=1,...,m).

            Тогда получим систему n+m неравенств

(zi,a)>0 (i=1,...,n+m),

которую будем решать относительно a. Если множество решений непусто, то любой его элемент a порождает решающее правило, безошибочное на обучающей выборке.

            Итерационный алгоритм решения этой системы чрезвычайно прост. Он основан на том, что для любого вектора x его скалярный квадрат (x,x) больше нуля. Пусть a ‑ некоторый вектор, претендующий на роль решения неравенств (zi,a)>0 (i=1,...,n+m), однако часть из них не выполняется. Прибавим те zi, для которых неравенства имеют неверный знак, к вектору a и вновь проверим все неравенства (zi,a)>0 и т.д. Если они совместны, то процесс сходится за конечное число шагов. Более того, добавление zi к a можно производить сразу после того, как ошибка ((zi,a)<0) обнаружена, не дожидаясь проверки всех неравенств ‑ и этот вариант алгоритма тоже сходится.

4.2.Заполнение пробелов в данных (прогнозирование значений)

4.2.1.Математический аппарат.

            Рассмотрим задачу поиска решения системы линейных уравнений 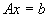, которая сводится к минимизации многочлена

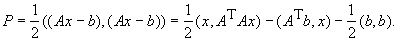
            Поэтому решение системы может производиться нейронной сетью. Простейшая сеть, вычисляющая градиент этого многочлена, не полносвязна, а состоит из двух слоев: первый с матрицей связей 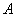, второй ‑ с транспонированной матрицей 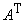. Постоянный единичный сигнал подается на связи с весами 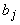 на первом слое. Минимизация этого многочлена, а значит и решение системы линейных уравнений, может проводиться так же, как и в общем случае, в соответствии с формулой .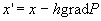

            Небольшая модификация позволяет вместо безусловного минимума многочлена второго порядка P искать точку условного минимума с условиями 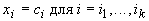, то есть точку минимума P в ограничении на аффинное многообразие, параллельное некоторым координатным плоскостям. Для этого вместо формулы


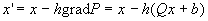
следует использовать:

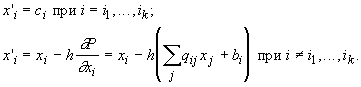
            Устройство, способное находить точку условного минимума многочлена второго порядка при условиях вида 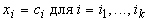 позволяет решать важную задачу ‑ заполнять пробелы в данных (и, в частности, строить линейную регрессию).

            Предположим, что получаемые в ходе испытаний векторы данных подчиняются многомерному нормальному распределению:

,

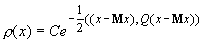где Mx ‑ вектор математических ожиданий координат, 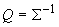, 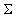‑ ковариационная матрица, n ‑ размерность пространства данных,

 .

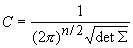            Матрица :

,

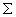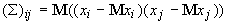где M ‑ символ математического ожидания, нижний индекс соответствует номеру координаты.

            В частности, простейшая оценка ковариационной матрицы по выборке дает:

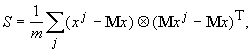
где m ‑ число элементов в выборке, верхний индекс j ‑ номер вектора данных в выборке, верхний индекс Т означает транспонирование, а Ä ‑ произведение вектора-столбца на вектор-строку (тензорное произведение).

            Пусть у вектора данных x известно несколько координат: 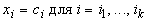. Наиболее вероятные значения неизвестных координат должны доставлять условный максимум показателю нормального распределения ‑ многочлену второго порядка 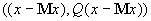 (при условии 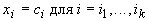). Эти же значения будут условными математическими ожиданиями неизвестных координат при заданных условиях.

            Таким образом, чтобы построить сеть, заполняющую пробелы в данных, достаточно сконструировать сеть для поиска точек условного минимума многочлена 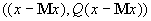 при условиях следующего вида: 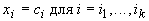. Матрица связей Q выбирается из условия 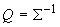, где S ‑ ковариационная матрица (ее оценка по выборке).

            На первый взгляд, пошаговое накопление 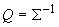 по мере поступления данных требует слишком много операций ‑ получив новый вектор данных требуется пересчитать оценку S, а потом вычислить 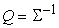. Можно поступать и по-другому, воспользовавшись формулой приближенного обращения матриц первого порядка точности:

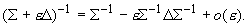
Если же добавка D имеет вид 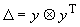, то

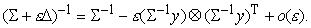
            Заметим, что решение задачи (точка условного минимума многочлена) не меняется при умножении Q на число. Поэтому полагаем:

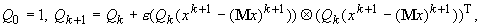
где 1 ‑ единичная матрица, e>0 ‑ достаточно малое число, 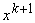 ‑ k+1-й вектор данных,  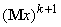‑ среднее значение вектора данных, уточненное с учетом :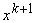

=

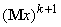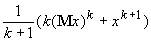
            В формуле для пошагового накопления матрицы Q ее изменение DQ при появлении новых данных получается с помощью вектора y=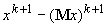, пропущенного через сеть: 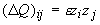, где z=Qy. Параметр e выбирается достаточно малым для того, чтобы обеспечить положительную определенность получаемых матриц (и, по возможности, их близость к истинным значениям Q).

            Если при обучении сети поступают некомплектные данные 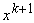 с отсутствием значений некоторых координат, то сначала эти значения восстанавливаются с помощью имеющейся сети, а потом используются в ее дальнейшем обучении.

4.2.2.Сети Хопфилда

            До сих пор речь шла о минимизации положительно определенных квадратичных форм и многочленов второго порядка. Однако самое знаменитое приложение полносвязных сетей связано с увеличением значений положительно определенных квадратичных форм (системы ассоциативной памяти ).

            Предположим, что задано несколько эталонных векторов данных 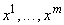 и при обработке поступившего на вход системы вектора x требуется получить на выходе ближайший к нему эталонный вектор. Мерой сходства в простейшем случае будем считать косинус угла между векторами ‑ для векторов фиксированной длины это просто скалярное произведение. Можно ожидать, что изменение вектора x по закону

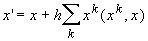
где h ‑ малый шаг, приведет к увеличению проекции x на те эталоны, скалярное произведение на которые 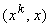 больше.

            Ограничимся рассмотрением эталонов, и ожидаемых результатов обработки с координатами 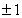. Развивая изложенную идею, приходим к дифференциальному уравнению

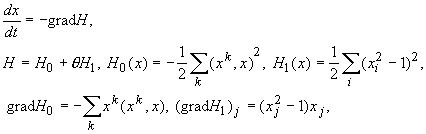
где верхними индексами обозначаются номера векторов-эталонов, нижними ‑ координаты векторов.

            Функция H называется «энергией» сети, она минимизируется в ходе функционирования. Слагаем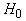ое  вводится для того, чтобы со временем возрастала проекция вектора x на те эталоны, которые к нему ближе, слагаемое 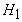 обеспечивает стремление координат вектора x к 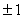. Параметр q определяет соотношение между интенсивностями этих двух процессов. Целесообразно постепенно менять q со временем, начиная с малых q<1, и приходя в конце концов к q>1.

            Матрица связей построенной сети определяется функцией 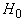, так как  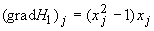вычисляется непосредственно при j-м нейроне без участия сети. Вес связи между i-м и j-м нейронами не зависит от направления связи и равен

.

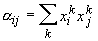            Эта простая формула имеет чрезвычайно важное значение для развития теории нейронных сетей. Вклад k-го эталона в связь между i-м и j-м нейронами (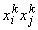) равен +1, если i-я и j-я координаты этого эталона имеют одинаковый знак, и равен ‑1, если они имеют разный знак.

            В результате возбуждение i-го нейрона передается j-му (и симметрично, от j-го к i-му), если у большинства эталонов знак i-й и j-й координат совпадают. В противном случае эти нейроны тормозят друг друга: возбуждение i-го ведет к торможению j-го, торможение i-го ‑ к возбуждению j-го (воздействие j-го на i-й симметрично). Это правило образования ассоциативных связей (правило Хебба) сыграло огромную роль в теории нейронных сетей.

4.2.2.1.Топология, обучение и алгоритм действий сети

            Топология нейронных сетей Хопфилда показана на рис. 4.2.2.1.1. Нейронная сеть состоит из N узлов. Выход каждого узла i передает значения всем другим узлам j (j=1...i-1,i=1...N) через веса W. В одной из первых версии сети Хопфилда каждый узел формирует взвешенную сумму N - 1 входов и пропускает результат выхода через жесткую ограничивающую нелинейную функцию

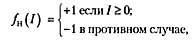
где I является суммой взвешенных входов в узел.

            Контролируемый процесс обучения в этом типе нейронной сети Хопфилда можно представить так. Сначала с использованием данной формулы на основе известной модели устанавливаются веса. Затем на сеть подается неизвестный входной образ, что вынуждает выход сети соответствовать неизвестной модели входа. Затем сеть, используя данную формулу, выполняет дискретные временные шаги. Когда выходные узлы остаются неизменными, сеть рассматривается как сходящаяся. После этого выходные узлы представляют собой модель, которая наилучшим образом соответствует неизвестной модели входа.

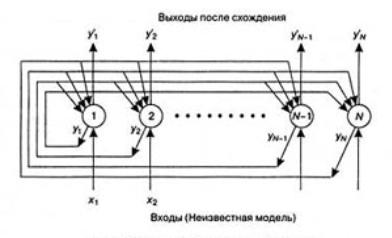
Модель нейронной сети Хопфилда

Рис. 4.2.2.1.1. Сеть Хопфилда

Ниже приведен  алгоритм действий для одной из первых версии сети Хопфилда.

Шаг 0. Определить топологию нейронной сети Хопфилда, как показано на рис. 5. Каждый узел принимает значение жесткой ограничивающей нелинейной функции.

Шаг 1. Назначить веса связи следующим образом:

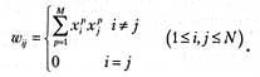
где W - вес связи между узлом i и узлом j, а x, который может принимать значения +1 или -1, является измерением i экземпляра модели p.

Шаг 2. Установить неизвестную модель входа следующим образом: y(t=0)=x(1<I

Шаг 3. Повторять следующее действие до схождения:

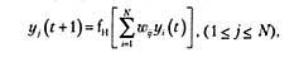
Нейронные сети - Формула

где f - жесткая ограничивающая нелинейная функция. Фактически сеть Хопфилда сходится, когда веса симметричны (т. е. W=W). Хопфилд (Hopfield, 1984) показал, что сеть сходится также в том случае, если градуированная функция нелинейности является сигмоидной.

4.2.3.Анализ баз данных с помощью нейронной сети Хопфилда

            Под анализом БД здесь понимается комплекс мероприятий, направленных на выявление скрытых закономерностей в базах данных с использованием аппарата искусственных нейронных сетей для решения задачи, которая в рамках задач автоматизированного интеллектуального анализа данных может трактоваться следующим образом.

  1. Качественное решение задачи определения значений полей БД, ассоциативно связанных с известными значениями других полей.
  2. Решение задачи прогнозирования значений набора полей БД при заданных значениях другого набора полей.

            Имея систему, схожую с ассоциативной памятью, а также формальные правила переноса информационного содержимого анализируемой базы данных в эту память, можно решить поставленную задачу. При этом используется ассоциативность такой системы и по значению некоторого фактора - “ключа” извлекаются ассоциативно близкие значения других факторов.

            Один из возможных путей реализации ассоциативной памяти состоит в том, чтобы построить распределенную динамическую систему или сеть из дискретных элементов, аттракторами которой являются типичные картины-образы (в настоящее время принято сопоставлять различным образам, запомненным нейронной сетью, установившиеся режимы или аттракторы соответствующей динамической системы). Каждая такая картина будет обладать своей областью притяжения, и всякое начальное условие, представляющее собой какую-то допустимую картину, обязано попасть в одну из ее областей притяжения. С течением времени в ходе эволюции эта начальная структура трансформируется в наиболее близкую из хранящихся в памяти структур-аттракторов, а именно в ту, области притяжения которой она принадлежала. Следовательно, подавая на вход в качестве начального условия для такой распределенной системы некоторую структуру, мы будем осуществлять ее автоматическое распознавание, которое будет параллельным. В роли такой распределенной динамической системы предлагается использовать искусственную нейронную сеть.

            Предлагаемое решение в общем виде выглядит следующим образом. Искусственная нейронная сеть обучается на записях анализируемой реляционной базы данных. В процессе обучения нейронная сеть становится гносеологической моделью обучающей БД. Полученную таким образом модель пользователь может использовать для прогнозирования и исследования ассоциативных связей, скрытых в базе данных.

            В качестве такой модели предлагается использовать сеть, представляющую собой конкретную реализацию динамической системы с ассоциативной памятью, предложенную Хопфилдом.

            Полем факторов для данной задачи является содержание реляционной базы данных. В представлении совокупности факторов в виде содержания реляционной базы данных заключается первичная подготовка данных для решения поставленной задачи. Тем самым задаются структурные отношения, и задача сводится к определению семантической близости содержимого полей заданной структуры. Так как бинарные искусственные нейронные сети оперируют двоичными векторами, то требуется дополнительная обработка исходных данных с целью приведения к виду, представляемому таким вектором. Необходимый для искусственной нейронной сети вектор получается конкатенацией двоичных векторов, представляющих поля реляционной базы данных

            Каждое поле реляционной базы данных обобщенно может быть отнесено к одному из двух типов: числовое, символьное. Значение символьного поля заносится в соответствующий каждому полю словарь. С тем, чтобы повысить эффективность процедур поиска значений в словаре и их кодирование, содержимое словарей ранжируется, повторяющиеся значения исключаются. Значения числовых полей представляются иначе. Диапазон значений каждого из числовых полей (к числовым полям относятся и те, которые содержат даты) разбивается на интервалы, а каждое конкретное значение представляется интервалом, к которому оно принадлежит. Точку на числовой оси можно представить вырожденным интервалом. Замена числовых значений интервалами обеспечивает большую гибкость представления. Аналогом словарей для числовых полей является перечень интервалов.

            После того, как были сформированы словари и наборы интервалов, они подвергаются кодированию. То есть каждому значению в словаре или интервалу в наборе ставится в соответствие двоичный код, представляющий впоследствии это значение или интервал в нейронной сети. Размерность кода (длина кода) для каждого словаря и набора (другими словами для каждого поля) определяется мощностью множества разнообразных значений в словаре или наборе, а также способом кодирования. Различные варианты кодирования могут существенно сказываться на качестве работы ассоциативной памяти, представленной нейронной сетью Хопфилда, что подтверждается результатами макетного моделирования.

            Формирование словарей и их кодирование является подготовительным этапом обучения нейронной сети. Каждая запись базы данных представляется в виде двоичного вектора и участвует в формировании весовых коэффициентов связей между формальными нейронами сети. Само обучение осуществляется в соответствии с правилом Хебба.

            Из обучения желательно удалить повторяющиеся записи базы данных. Так как повторная запись вектора в ассоциативную память, представленную нейронной сетью неблагоприятно сказывается на энергетическом ландшафте этой сети. А именно, удваивается глубина энергетического минимума соответствующего такому вектору. Более глубокий минимум обычно имеет более широкую область притяжения, а это уменьшает области притяжения соседних минимумов и искажает соответствующие притягивающие векторы. В предельном случае это может привести к тому, что в системе останется всего один очень глубокий минимум энергии, область притяжения которого захватывает все возможные спиновые конфигурации. У системы формируется как бы “навязчивая идея”, что, конечно же, крайне нежелательно.

            Существуют различные версии сетей Хопфилда сходные в структуре, но несколько отличные в функционировании. Здесь рассматриваются только бинарные (возможно два состояния нейрона: +1 и -1) нейросети Хопфилда с дискретным функционированием во времени. Спецификой объединяющей такие сети является их асинхронность функционирования. То есть в отличии от синхронного функционирования, при котором состояние всех нейронов сети определяется одновременно, асинхронное функционирование подразумевает в каждый конкретный момент времени возможность переключения только одного нейрона.

            В модели Хопфилда могут быть реализованы детерминированный и/или стохастический (с имитацией “отжига”) алгоритмы. Процесс функционирования нейронной сети является многоитерационным. Каждая итерация включает в себя два шага: выбор нейрона-кандидата, формирование состояния выбранного нейрона-кандидата.

            Отличие стохастического функционирования от детерминированного заключается в методе выбора нейрона-кандидата. При стохастическом кандидатом на переключение является нейрон, выбранный случайно с помощью датчика случайных чисел. Таким образом, возможны такие ситуации, что в процессе функционирования состояние некоторых нейронов не анализировалось. При детерминированном функционировании нейроны становятся кандидатами на изменение своего состояния в порядке следования своих номеров.

            В алгоритмах с имитацией “отжига” изменение состояния нейрона-кандидата носит вероятностный характер. Если в результате изменения состояния на противоположное полная энергия сети понизится, то состояние нейрона меняется на противоположное. Иначе состояние нейрона меняется на противоположное с определенной вероятностью, зависящей от параметра, называемого "температурой" сети, имитирующей уровень теплового шума. На первой итерации функционирования нейросети устанавливается начальное значение температуры (максимальное значение), затем постепенно через некоторое количество итераций значение температуры уменьшается. Итерационный процесс прекращается, когда температура достигает конечного значения (минимальное значение).

            Если сравнивать между собой алгоритмы без “отжига” и с имитацией “отжига”, то у первых множество преимуществ перед вторыми (проще, требуют меньшее количество итераций, обладают большей точностью - если энергетический ландшафт вблизи глобального минимума не изрезан локальными минимумами). Но, если энергетический ландшафт содержит множество локальных минимумов, то алгоритмы с имитацией “отжига” ведут себя лучше (с точки зрения критерия качества функционирования). Подтверждением последнего утверждения могут служить данные макетного моделирования.

4.2.3.1.Этапы работы при анализе базы данных с использованием нейронной сети.

            Использование нейронной сети Хопфилда для анализа базы данных включает в себя следующие этапы:

1.     Формирование SQL-запроса для работы с нейронной сетью.

2.     Формирование словаря содержимого полей SQL-запроса.

3.     Обучение нейронной сети.

4.     Поиск ассоциаций или прогноз значений полей БД.

            Последний этап в свою очередь включает в себя следующие этапы:

            1. Формирование запроса. На этом этапе пользователь выбирает часть полей БД и придает им некоторые значения (используя соответствующие этим полям словари значений и наборы интервалов). В процессе функционирования система будет прогнозировать значения других полей (отличных от задаваемых пользователем) подобно ассоциативной памяти.

            2. Подготовка входного вектора сети. На этом этапе для нейронной сети формируется входной вектор. Он “собирается” из подвекторов, соответствующих полям базы данных. При формировании вектора нулевые разряды подвекторов заменяются на (-1). Те подвектора, чьи значения задает пользователь, называются “замороженными”. Значения других подвекторов формируются с использованием датчика случайных чисел.

            3. Циклы функционирования нейронной сети. Этот этап включает в себя ряд циклов функционирования нейронной сети. Перед каждым циклом на нейронную сеть подается входной вектор, сформированный на предыдущем этапе функционирования. Нейронная сеть функционирует в соответствии с одним из четырех выше названных алгоритмов. Каждый цикл функционирования нейронной сети состоит из многократных итераций, при этом каждая итерация в свою очередь включает два вышеописанных этапа (выбор нейрона-кандидата, формирование состояния выбранного нейрона-кандидата). Следует заметить, что нейроны соответствующие “замороженным” подвекторам, не могут быть выбраны в качестве нейрона-кандидата, и, следовательно, они не меняют своего состояния в течении всего функционирования. По завершению первого цикла полученный нейронной сетью вектор и значение энергии сети запоминается в специальном буфере. В конце каждого последующего цикла значение энергии сети сравнивается с запомненным значением из буфера. Если текущее значение энергии меньше запомненного в буфере, то текущее состояние сети (состояние сети представляет собой вектор в качестве компонент которого выступают состояния нейронов) замещает в буфере ранее запомненный вектор.

            4. Формирование выходного вектора. Это чисто формальный этап, когда вектор, сохраненный в буфере, выдается системой как вектор-ответ, восстановленный ассоциативной памятью по заданному пользователем фрагменту.

4.3.Сети Кохонена для кластер-анализа и классификации без учителя.

4.3.1.Математический аппарат

            Построение отношений на множестве объектов - одна из самых загадочных и открытых для творчества областей применения искусственного интеллекта. Первым и наиболее распространенным примером этой задачи является классификация без учителя.

            Задан набор объектов, каждому объекту сопоставлен вектор значений признаков (строка таблицы). Требуется разбить эти объекты на классы эквивалентности.

            Зачем нужно строить отношения эквивалентности между объектами? В первую очередь - для фиксации знаний. Люди накапливают знания о классах объектов - это практика многих тысячелетий, зафиксированная в языке: знание относится к имени класса (пример стандартной древней формы: "люди смертны", "люди" - имя класса). В результате классификации как бы появляются новые имена и правила их присвоения.

            Для каждого нового объекта мы должны сделать следующее:

1)     найти класс, к которому он принадлежит;

2)     использовать новую информацию, полученную об этом объекте, для исправления (коррекции) правил классификации.

            Какую форму могут иметь правила отнесения к классу? Веками освящена традиция представлять класс его "типичным", "средним", "идеальным" и т.п. элементом. Этот типичный объект является идеальной конструкцией, олицетворяющей класс.

            Отнесение объекта к классу проводится путем его сравнения с типичными элементами разных классов и выбора ближайшего. Правила, использующие типичные объекты и меры близости для их сравнения с другими, очень популярны и сейчас.

            Простейшая мера близости объектов - квадрат евклидового расстояния между векторами значений их признаков (чем меньше расстояние ‑ расстояние - тем ближе объекты). Соответствующее определение признаков типичного объекта - среднее арифметическое значение признаков по выборке, представляющей класс.

            Другая мера близости, естественно возникающая при обработке сигналов, изображений и т.п. - квадрат коэффициента корреляции (чем он больше, тем ближе объекты). Возможны и иные варианты - все зависит от задачи.

            Если число классов m заранее определено, то задачу классификации без учителя можно поставить следующим образом.

            Пусть {xp } - векторы значений признаков для рассматриваемых объектов и в пространстве таких векторов определена мера их близости r{x,y}. Для определенности примем, что чем ближе объекты, тем меньше r. С каждым классом будем связывать его типичный объект. Далее называем его ядром класса. Требуется определить набор из m ядер y1 , y2 , ... ym и разбиение {xp} на классы:

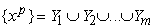
минимизирующее следующий критерий

,

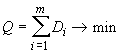где для каждого (i-го) класса 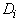 ‑ сумма расстояний от принадлежащих ему точек выборки до ядра класса:

.

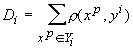            Минимум Q берется по всем возможным положениям ядер 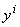 и всем разбиениям {xp}на m классов Yi.

            Если число классов заранее не определено, то полезен критерий слияния классов: классы Yi и Yj сливаются, если их ядра ближе, чем среднее расстояние от элемента класса до ядра в одном из них. (Возможны варианты: использование среднего расстояния по обоим классам, использование порогового коэффициента, показывающего, во сколько раз должно расстояние между ядрами превосходить среднее расстояние от элемента до ядра и др.)

            Использовать критерий слияния классов можно так: сначала принимаем гипотезу о достаточном числе классов, строим их, минимизируя Q, затем некоторые Yi объединяем, повторяем минимизацию Q с новым числом классов и т.д.

            Существует много эвристических алгоритмов классификации без учителя, основанных на использовании мер близости между объектами. Каждый из них имеет свою область применения, а наиболее распространенным недостатком является отсутствие четкой формализации задачи: совершается переход от идеи кластеризации прямо к алгоритму, в результате неизвестно, что ищется (но что-то в любом случае находится, иногда - неплохо).

            Сетевые алгоритмы классификации без учителя строятся на основе итерационного метода динамических ядер. Опишем его сначала в наиболее общей абстрактной форме. Пусть задана выборка предобработанных векторов данных {xp}. Пространство векторов данных обозначим E. Каждому классу будет соответствовать некоторое ядро a. Пространство ядер будем обозначать A. Для каждых xÎE и aÎA определяется мера близости d(x,a). Для каждого набора из k ядер a1,...,ak и любого разбиения {xp} на k классов {xp}=P1ÈP2È...ÈPk определим критерий качества:

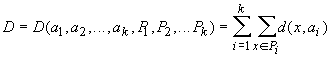
            Требуется найти набор a1,...,ak и разбиение {xp}=P1ÈP2È...ÈPk, минимизирующие D.

            Шаг алгоритма разбивается на два этапа:

1)     1-й этап - для фиксированного набора ядер a1,...,ak ищем минимизирующее критерий качества D разбиение {xp}=P1ÈP2È...ÈPk; оно дается решающим правилом: xÎPi, если d(x ,ai )<d(x ,aj ) при i¹j, в том случае, когда для x минимум d(x,a) достигается при нескольких значениях i, выбор между ними может быть сделан произвольно;

2)     2-й этап - для каждого Pi (i=1,...,k), полученного на первом этапе, ищется aiÎA, минимизирующее критерий качества (т.е. слагаемое в D для данного i -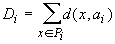

            Начальные значения a1,...,ak, {xp}=P1ÈP2È...ÈPk выбираются произвольно, либо по какому-нибудь эвристическому правилу.

            На каждом шаге и этапе алгоритма уменьшается критерий качества D, отсюда следует сходимость алгоритма - после конечного числа шагов разбиение {xp}=P1ÈP2È...ÈPk уже не меняется.

            Если ядру ai сопоставляется элемент сети, вычисляющий по входному сигналу x функцию d(x,ai), то решающее правило для классификации дается интерпретатором "победитель забирает все": элемент x принадлежит классу Pi, если выходной сигнал i-го элемента d(x,ai) меньше всех остальных

            Единственная вычислительная сложность в алгоритме может состоять в поиске ядра по классу на втором этапе алгоритма, т.е. в поиске aÎA, минимизирующего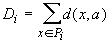

            В связи с этим, в большинстве конкретных реализаций метода мера близости d выбирается такой, чтобы легко можно было найти a, минимизирующее D для данного P .

В простейшем случае пространство ядер A совпадает с пространством векторов x, а мера близости d(x,a) - положительно определенная квадратичная форма от x‑a, например, квадрат евклидового расстояния или другая положительно определенная квадратичная форма. Тогда ядро ai, минимизирующее Di, есть центр тяжести класса Pi :

,

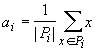где |Pi| ‑ число элементов в Pi.

            В этом случае также упрощается и решающее правило, разделяющее классы. Обозначим d(x,a)=(x-a,x-a), где (.,.) ‑ билинейная форма (если d - квадрат евклидового расстояния между x и a, то (.,.) - обычное скалярное произведение). В силу билинейности

d(x,a)=(x‑a,x‑a)=(x,x)‑2(x,a)+(a,a).

            Чтобы сравнить d(x,ai) для разных i и найти среди них минимальное, достаточно вычислить линейную неоднородную функцию от x:

d1(x,ai) = (ai,ai)‑2(x,ai).

            Минимальное значение d(x,ai) достигается при том же i, что и минимум d1(x,ai), поэтому решающее правило реализуется с помощью k сумматоров, вычисляющих d(x,a) и интерпретатора, выбирающего сумматор с минимальным выходным сигналом. Номер этого сумматора и есть номер класса, к которому относится x.

            Пусть теперь мера близости - коэффициент корреляции между вектором данных и ядром класса:

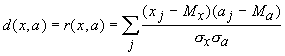
где 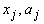‑ координаты векторов,  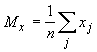(и аналогично 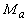), n ‑ размерность пространства данных, (и аналогично ).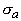

            Предполагается, что данные предварительно обрабатываются (нормируются и центрируются) по правилу:

.

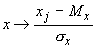            Точно также нормированы и центрированы векторы ядер a. Поэтому все обрабатываемые векторы и ядра принадлежат сечению единичной евклидовой сферы (||x||=1) гиперплоскостью (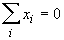). В таком случае .

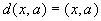            Задача поиска ядра для данного класса P имеет своим решением

.

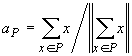            В описанных простейших случаях, когда ядро класса точно определяется как среднее арифметическое (или нормированное среднее арифметическое) элементов класса, а решающее правило основано на сравнении выходных сигналов линейных адаптивных сумматоров, нейронную сеть, реализующую метод динамических ядер, называют сетью Кохонена. В определении ядер a для сетей Кохонена входят суммы 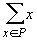. Это позволяет накапливать новые динамические ядра, обрабатывая по одному примеру и пересчитывая ai после появления в Pi нового примера. Сходимость при такой модификации, однако, ухудшается.

4.3.2.Сети Кохонена. Топология, обучение и алгоритм действий сети.

            Нейронная сеть, изображенная на рис. 4.3.2.1, представляет собой двухуровневую самоорганизующуюся карту Кохонена (SOFM - self-organizing feature map). Узлы нижнего уровня (узлы входа) получают входящие значения, представленные точками выборочных данных. Узлы верхнего уровня (узлы выхода) будут давать карту организации моделей входа после неконтролируемого процесса обучения. На этом рисунке верхний уровень имеет вид одномерного множества (хотя может быть представлен и в виде двумерного множества). Каждый узел нижнего уровня связан с каждым узлом верхнего уровня через связи переменного веса.

            Неконтролируемый процесс обучения в SOFM можно описать следующим образом. Сначала веса связей принимают значения небольших случайных чисел. Поступающий входной вектор, представленный точками выборочных данных, образован узлами входа. Затем входной вектор через связи передается к выходным узлам. Активация узлов выхода зависит от входов. В отборе по принципу «победитель получает все» становится активным выходной узел с весами, наиболее близкими к входному вектору. На стадии обучения веса обновляются согласно следующему правилу:

W(новый)=W(старый)=[X-w(старый)]

где W — это матрица весов; X — вектор входа, а n — параметр обучения (0 < n < 1), который уменьшается с течением времени.

            Обновление весов происходит только для активного выходного узла и его топологических соседей (рис. 4). Вначале окрестность велика, а затем она постепенно уменьшается. Когда параметр обучения n уменьшится до нуля при неконтролируемом обучении SOFM, процесс обучения остановится.

            После представления достаточного количества входных векторов с помощью весов можно будет определить такие кластеры, в которых локальная функция плотности центров кластеров будет иметь тенденцию бесконечно приближаться к вероятностной функции плотности входных векторов. Веса будут организованы таким образом, что узлы, участие которых в топологическом сходстве чувствительно к значению входа, будут подобными. Выходные узлы в SOFM, таким образом, будут организованы и представлены в виде кластеров в самоорганизующейся карте.

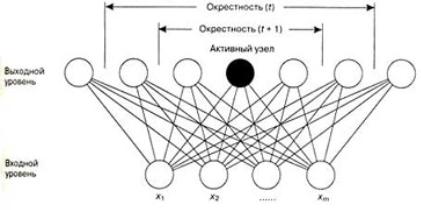
Самоорганизующиеся карты Коонена (Kohonen)

Рис. 4.3.2.1. Сеть Кохонена

            Типичный алгоритм действий самоорганизующихся карт можно представить следующим образом.

Шаг 0. Инициализировать веса от M входов к N выходным узлам малыми случайными значениями. Установить начальную функцию окрестности nei(t=0)=k, где t — время, а k — произвольное число (например, k=N). Установить начальный параметр обучения n (t=0)=р, где 0 < р < 1.

Шаг 1. Представить наблюдение.

Шаг 2. Вычислить

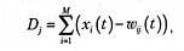
где х(t) является входом в узел i в момент времени t, а w(t) — вес связи входного узла i и выходного узла j в момент времени t.

Шаг 3. Выбрать победителя, т. е. такой выходной узел J, что D=min(D)

Шаг 4. Определить множество 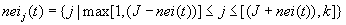. Обновить веса следующим образом

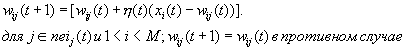
Шаг 5. Если 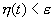, где 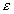 - заранее определенная малая положительная константа, тогда СТОП; в противном случае вычислить

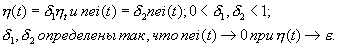
Установить 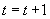 и перейти к шагу 2.

4.3.3.Различные способы использования полученных классификаторов.

            Рассмотрим различные способы использования полученных классификаторов.

  1. Базовый способ: для вектора данных xi и каждого ядра ai вычисляется yi=d(x,ai) (условимся считать, что правильному ядру отвечает максимум d, изменяя, если надо, знак d); по правилу «победитель забирает все» строка ответов yi преобразуется в строку, где только один элемент, соответствующий максимальному yi, равен 1, остальные ‑ нули. Эта строка и является результатом функционирования сети. По ней может быть определен номер класса (номер места, на котором стоит 1) и другие показатели.
  2. Метод аккредитации: за слоем элементов базового метода, выдающих сигналы 0 или 1 по правилу "победитель забирает все" (далее называем его слоем базового интерпретатора), надстраивается еще один слой выходных сумматоров. С каждым (i-м) классом ассоциируется q-мерный выходной вектор zi с координатами zij . Он может формироваться по-разному: от двоичного представления номера класса до вектора ядра класса. Вес связи, ведущей от i-го элемента слоя базового интерпретатора к j-му выходному сумматору определяется в точности как zij . Если на этом i-м элементе базового интерпретатора получен сигнал 1, а на остальных - 0, то на выходных сумматорах будут получены числа zij.
  3. Нечеткая классификация. Пусть для вектор данных x обработан слоем элементов, вычисляющих yi=d(x,ai). Идея дальнейшей обработки состоит в том, чтобы выбрать из этого набора {yi} несколько самых больших чисел и после нормировки объявить их значениями функций принадлежности к соответствующим классам. Предполагается, что к остальным классам объект наверняка не принадлежит. Для выбора семейства G наибольших yi определим следующие числа: 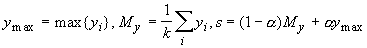,где число a характеризует отклонение "уровня среза" s от среднего значения 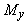 aÎ[-1,1], по умолчанию обычно принимается a=0. Множество J={i|yiÎG} трактуется как совокупность номеров тех классов, к которым может принадлежать объект, а нормированные на единичную сумму неотрицательные величины 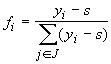 (при iÎJ и f = 0 в противном случае)  интерпретируются как значения функций принадлежности этим классам.
  4. Метод интерполяции надстраивается над нечеткой классификацией аналогично тому, как метод аккредитации связан с базовым способом. С каждым классом связывается q-мерный выходной вектор zi. Строится слой из q выходных сумматоров, каждый из которых должен выдавать свою компоненту выходного вектора. Весовые коэффициенты связей, ведущих от того элемента нечеткого классификатора, который вычисляет fi, к j-му выходному сумматору определяются как zij. В итоге вектор выходных сигналов сети есть

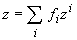
4.3.4.Общий подход к построению классификатора на основе нейронных сетей.

            Работа с данными

    1. Составить базу данных из примеров, характерных для данной задачи
    2. Разбить всю совокупность данных на два множества: обучающее и тестовое (возможно разбиение на 3 множества: обучающее, тестовое и подтверждающее).

            Предварительная обработка

  1. Выбрать систему признаков, характерных для данной задачи, и преобразовать данные соответствующим образом для подачи на вход сети (нормировка, стандартизация и т.д.). В результате желательно получить линейно отделяемое пространство множества образцов.
  2. Выбрать систему кодирования выходных значений (классическое кодирование, 2 на 2 кодирование и т.д.)

            Конструирование, обучение и оценка качества сети:

  1. Выбрать топологию сети: количество слоев, число нейронов в слоях и т.д.
  2. Выбрать функцию активации нейронов (например "сигмоида")
  3. Выбрать алгоритм обучения сети
  4. Оценить качество работы сети на основе подтверждающего множества или другому критерию, оптимизировать архитектуру (уменьшение весов, прореживание пространства признаков)
  5. Остановится на варианте сети, который обеспечивает наилучшую способность к обобщению и оценить качество работы по тестовому множеству.

            Использование и диагностика

  1. Выяснить степень влияния различных факторов на принимаемое решение (эвристический подход).
  2. Убедится, что сеть дает требуемую точность классификации (число неправильно распознанных примеров мало)
  3. При необходимости вернутся на этап 2, изменив способ представления образцов или изменив базу данных.
  4. Практически использовать сеть для решения задачи.

            Для того, чтобы построить качественный классификатор, необходимо иметь качественные данные. Никакой из методов построения классификаторов, основанный на нейронных сетях или статистический, никогда не даст классификатор нужного качества, если имеющийся набор примеров не будет достаточно полным и представительным для той задачи, с которой придется работать системе.

Заключение

            В данной работе описаны некоторые применения нейросетевых методов обработки информации для решения задач прогнозирования, кластеризации и классификации, каторые относятся к базовым задачам технологии Data Mining.

            К настоящему времени накоплен очень большой опыт по применению нейронных сетей для решения задач поиска скрытых знаний в различных проблемных областях: климатологии, медицине, психологии и политологии, диагностике и оптимальном управлении в технических системах и т.д. Нейронные сети позволяют решать различные неформализованные задачи (задачи, где алгоритм решения неизвестен). Исследователь при этом получает очень эффективную модель проблемной области и может очень просто моделировать различные ситуации, предъявляя сети различные данные и оценивания ответ, выдаваемый сетью. Нейронные сети могут применяться и в ситуациях, когда известен сравнимый по точности прогноза метод решения, но критично, например, время получения результата, поскольку обученная нейронная сеть решает предъявляемую ей задачу очень быстро.

            Большинство пользователей (от простых пользователей нейросетевых экспертных систем до специалистов-исследователей в области нейроинформатики), применяющих нейронных сети, отмечают единственный существенный недостаток нейронных сетей. А именно, человеку не понятно, какие "рассуждения" используются внутри нейронной сети при решении задачи. Иными словами, очень трудно понять процесс получения сетью результата. Первый шаг в этом направлении уже сделан. Сеть может количественно оценить влияние входных признаков на точность решения задачи. Ранжируя входные признаки по этим показателям значимости и последовательно исключая наименее значимые (дообучая при этом сеть извлекать нужную информацию из меньшего объема данных), можно получить минимально необходимый для правильного решения задачи набор входных параметров. Это уже дает информацию для содержательного анализа.

            В настоящее время ведутся работы по созданию новой технологии, позволяющих не только решать задачи с помощью обучаемых нейронных сетей, но и генерировать вербализованное (на естественном языке) описание процесса решения сетью задачи. Фактически, по таблице экспериментальных данных, описывающих проблемную область, можно будет получить новое знание - явный алгоритм решения поставленной неформализованной задачи.


Список использованных источников.

1. А.Н.Горбань, В.Л.Дунин-Барковский, А.Н.Кирдин и др. Нейроинформатика. - Новосибирск: Наука. Сибирское предприятие РАН, 1998. - 296с.

 

2. А.А.Барсегян и др. Методы и модели анализа данных: OLAP и Data Mining.СПб.: БХВ-Петербург,2004.-336с.

 

3. Ф.Уоссермен. Нейрокомпьютерная техника: теория и практика. М. Мир - 1992

 

4. А. В. Гаврилов, В. М. Канглер. Использование искусственных нейронных сетей для анализа данных.- СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. - 1999. - №3(16). – с. 56-63.

 

5. www.basegroup.ru

 

6. www.neuronet.alo.ru