2. АСИМПТОТИЧЕСКИ ОПТИМАЛЬНОЕ
ГРУППИРОВАНИЕ И ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ
2.1. Асимптотическая эффективность
оценок и асимптотически оптимальное группирование данных
2.2. Решение задачи асимптотически
оптимального группирования
2. АСИМПТОТИЧЕСКИ ОПТИМАЛЬНОЕ ГРУППИРОВАНИЕ И ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ
2.1. Асимптотическая эффективность оценок и асимптотически оптимальное группирование данных
Группирование наблюдений используется
как при оценке параметров распределений, так и в задачах проверки
статистических гипотез. До настоящего момента при группировании область
определения случайной величины разбивается на интервалы равной длины или равной
вероятности. Такой подход рассматривается в наиболее часто используемых для
руководства источниках. Всякая группировка
данных по сравнению с негруппированной выборкой ведет к потере информации, понимаемой в общем широком смысле. И это, естественно,
отражается на качестве статистических выводов. Очевидно, что чем меньше потери
информации, тем надежнее получаемые результаты. Постановка задачи
асимптотически оптимального группирования вытекает непосредственно из
асимптотических свойств оценок и критериев. Её решение, минимизирующее потери
в количестве информации Фишера, повышает качество статистических выводов как
при оценивании, так и при проверке гипотез. В данной главе задача
асимптотически оптимального группирования наблюдений рассматривается
относительно оценивания параметров. Вопросы асимптотически оптимального
группирования данных в связи с критериями согласия подробно рассматривается ниже.
ОМП параметров распределений по
группированным данным являются асимптотически эффективными (если они
существуют и единственны). И их асимптотическая дисперсия определяется
соотношением
![]() ,
,
где
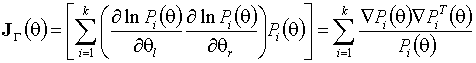 - информационная
матрица Фишера по группированным наблюдениям.
- информационная
матрица Фишера по группированным наблюдениям.
Это же справедливо для оценок,
получаемых в результате минимизации статистик ![]()
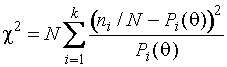 ,
,
модифицированный
статистики ![]()
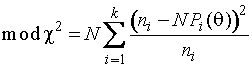 ,
,
где
![]() заменяется на 1, если
заменяется на 1, если ![]() . расстояния Хеллингера
. расстояния Хеллингера
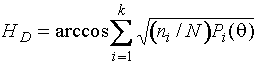 ,
,
дивергенции
Кульбака-Лейблера
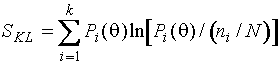 ,
,
меры
расхождения Холдейна
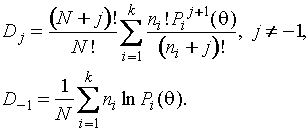
Все эти методы, как уже упоминалось,
при соответствующих условиях регулярности дают состоятельные и асимптотически
эффективные оценки.
Аналогично,
асимптотически эффективными являются оценки параметров сдвига и масштаба по
выборочным квантилям, рассматриваемые ниже в данной главе.
Элементы
информационной матрицы зависят от граничных точек интервалов, так как 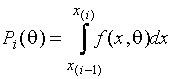 . В случае, когда функция плотности распределения
определяется скалярным параметром или осуществляется оценивание только одного
параметра при известных остальных, целью задачи асимптотически оптимального
группирования является минимизация асимптотической дисперсии ОМП по группированным
данным. И эта задача сводится к максимизации информационного количества Фишера
о параметре по группированной выборке, т.е. к решению задачи нелинейного
программирования
. В случае, когда функция плотности распределения
определяется скалярным параметром или осуществляется оценивание только одного
параметра при известных остальных, целью задачи асимптотически оптимального
группирования является минимизация асимптотической дисперсии ОМП по группированным
данным. И эта задача сводится к максимизации информационного количества Фишера
о параметре по группированной выборке, т.е. к решению задачи нелинейного
программирования
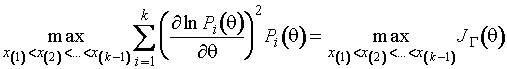 , (2.1.1)
, (2.1.1)
где ![]() - количество
информации Фишера о параметре по группированным наблюдениям.
- количество
информации Фишера о параметре по группированным наблюдениям.
Решение такой задачи для параметра
экспоненциального распределения при ![]() впервые было получено
в [205], а для параметров нормального распределения при известном одном из них
решения приведены в [65].
впервые было получено
в [205], а для параметров нормального распределения при известном одном из них
решения приведены в [65].
При оценивании вектора параметров мы
имеем дело с информационной матрицей. В этом случае в качестве критериев
оптимальности могут быть выбраны различные функционалы от асимптотической дисперсионной
матрицы, но наиболее естественно минимизировать обобщенную асимптотическую
дисперсию (максимизировать ![]() ), т.е. решать задачу нелинейного программирования вида
), т.е. решать задачу нелинейного программирования вида
![]() . (2.1.2)
. (2.1.2)
Как будет показано, стремление
использовать критерии согласия, предусматривающие группировку данных, таким
образом, чтобы они обладали максимальной мощностью (по крайней мере при близких
альтернативах), приводит к этой же самой задаче асимптотически оптимального
группирования. И, таким образом, полученные ее решения могут эффективно
использоваться как в задачах оценивания, так и в задачах проверки
статистических гипотез.
В то же время до настоящего момента при
оценивании параметров распределений с использованием группировки данных или
проверке согласия по критерию Пирсона или родственному ему, а также при построении
гистограмм область определения случайной величины разбивают на интервалы
равной длины или равной вероятности. Причем в основном осуществляется
разбиение на интервалы равной длины с последующим объединением тех смежных
интервалов, в которые попало малое число наблюдений. Такое группирование
рассматривается в наиболее часто используемых для руководства источниках.
Задачи (2.1.1-2.1.2) представляют собой
задачи нелинейного программирования с допустимым множеством решений,
задаваемым линейной системой ограничений, и нелинейной целевой функцией. При
вогнутой целевой функции эти задачи имеют единственное решение. Но в таких
задачах вогнутость целевой функции обеспечивается не всегда, и в некоторых случаях
задача асимптотически оптимального группирования оказывается многоэкстремальной.
Задачи асимптотически оптимального группирования для конкретных законов
распределения решались нами в работах [29,31,32,37, 38,39,69,70,71,72].
Аналогичная задача, связанная с оцениванием параметров регрессионных моделей
по группированным наблюдениям и асимптотически оптимальным группированием при
их оценивании, решалась в работах [33,34,35].
Вид системы ограничений позволяет
достаточно просто, используя метод штрафных функций [175,181,61] свести
условную задачу оптимизации (2.1.1) или (2.1.2) к безусловной. А для решения
последней использовать различные алгоритмы поиска минимума функции ![]() переменных [25,
26,44,47,55,111,130,135,142,], в том числе методы сопряженных градиентов
[137,175,68], вращающихся координат Розенброка [177], алгоритмы переменной
метрики [177]. В процессе решения задач асимптотически оптимального
группирования был сформирован комплекс программ оптимизации, который
применялся для решения задач оптимизации из различных областей [49],
использутся в учебном процессе [80], а некоторые алгоритмы реализованы в
программной системе [76].
переменных [25,
26,44,47,55,111,130,135,142,], в том числе методы сопряженных градиентов
[137,175,68], вращающихся координат Розенброка [177], алгоритмы переменной
метрики [177]. В процессе решения задач асимптотически оптимального
группирования был сформирован комплекс программ оптимизации, который
применялся для решения задач оптимизации из различных областей [49],
использутся в учебном процессе [80], а некоторые алгоритмы реализованы в
программной системе [76].
В следующем разделе рассматривается
задача асимптотически оптимального группирования для конкретных законов
распределения, в основном, для тех, для которых решение получается в виде
инвариантном относительно параметров распределения.
2.2. Решение задачи асимптотически оптимального группирования
В данном разделе представлены
результаты решения задачи асимптотически оптимального группирования для
законов распределения, наиболее часто используемых в приложениях, для которых
решение удалось получить в виде, инвариантном относительно параметров
распределения.
В прил. П1.1 приведены асимптотически
оптимальные граничные точки для экспоненциального
распределения в виде ![]() , максимизирующие информационное количество Фишера по
группированным данным
, максимизирующие информационное количество Фишера по
группированным данным
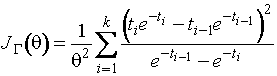 ,
,
где
![]() , а функция плотности экспоненциального распределения описывается
выражением
, а функция плотности экспоненциального распределения описывается
выражением ![]() . Для числа интервалов
. Для числа интервалов ![]() асимптотически
оптимальные граничные точки приведены [65], в [69] эти данные были проверены и
таблица продолжена до
асимптотически
оптимальные граничные точки приведены [65], в [69] эти данные были проверены и
таблица продолжена до ![]() . В этой же таблице приложения даны значения относительной
асимптотической информации, равной
. В этой же таблице приложения даны значения относительной
асимптотической информации, равной
![]() ,
,
где
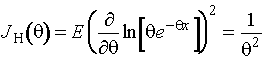 - информационное
количество Фишера о
- информационное
количество Фишера о ![]() по негруппированным
наблюдениям. В прил. П1.2 представлены соответствующие значения оптимальных
вероятностей. Заметим, что величина
по негруппированным
наблюдениям. В прил. П1.2 представлены соответствующие значения оптимальных
вероятностей. Заметим, что величина ![]() позволяет делать
заключение о качестве проводимого группирования. Для сравнения дадим
вычисленные значения относительной асимптотической информации при разбиении на
интервалы равной вероятности. Оказалось, что
позволяет делать
заключение о качестве проводимого группирования. Для сравнения дадим
вычисленные значения относительной асимптотической информации при разбиении на
интервалы равной вероятности. Оказалось, что ![]() для
для ![]() и
и ![]() для
для ![]() , в то время как оптимальному группированию уже при
, в то время как оптимальному группированию уже при ![]() соответствует значение
соответствует значение
![]() .
.
На рис. 2.2.1 представлен график относительных потерь
в информационном количестве Фишера при равновероятном группировании для экспоненциального
распределения в зависимости от числа интервалов. Видно, что потери особенно
велики при малом числе интервалов. Этот же график отражает и относительную
величину возрастания асимптотической дисперсии оценки.
Информационное количество Фишера о
параметре распределения Рэлея на
одно наблюдение по группированным данным описывается выражением
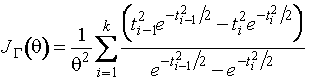 ,
,
где ![]() . Информационное количество Фишера на одно наблюдение по
негруппированным данным
. Информационное количество Фишера на одно наблюдение по
негруппированным данным
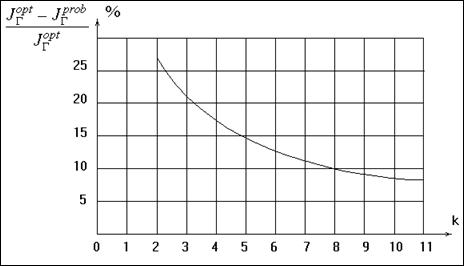
Рис. 2.2.1.
Относительные потери в информационном количестве Фишера при равновероятном группировании
по сравнению с асимптотически оптимальным группированием для
экспоненциального распределения
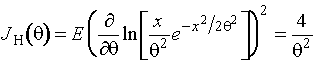 .
.
Асимптотически
оптимальные граничные точки интервалов группирования [69,29] в форме ![]() , максимизирующие
, максимизирующие ![]() , приводятся в прил. П1.3. В нем же даны соответствующие
значения относительной асимптотической информации
, приводятся в прил. П1.3. В нем же даны соответствующие
значения относительной асимптотической информации ![]() , позволяющей судить о качестве группирования. Значения
вероятностей, которые соответствуют граничным точкам, содержатся в прил. П1.2.
, позволяющей судить о качестве группирования. Значения
вероятностей, которые соответствуют граничным точкам, содержатся в прил. П1.2.
Выражение для информационного
количества Фишера о параметре распределения
Максвелла по группированным наблюдениям имеет вид
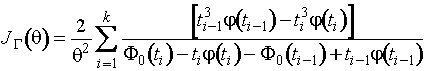 ,
,
где
![]() ;
; ![]() ;
; 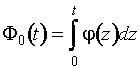 .
.
По негруппированным данным имеем
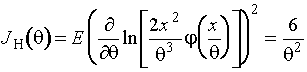 .
.
Полученные асимптотически оптимальные
граничные точки интервалов группирования [62,69] в форме ![]() и соответствующие
значения относительной асимптотической информации
и соответствующие
значения относительной асимптотической информации ![]() приведены в прил.
П1.4, а значения соответствующих вероятностей - в прил. П1.5.
приведены в прил.
П1.4, а значения соответствующих вероятностей - в прил. П1.5.
Рассмотрим задачу асимптотически
оптимального группирования для
распределения модуля многомерного нормального вектора. В общем случае
функция плотности этого распределения имеет вид
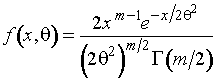 ,
,
где
![]() ;
; ![]() - размерность
соответствующего многомерного нормального распределения. При известном
- размерность
соответствующего многомерного нормального распределения. При известном ![]() распределение
полностью определяется параметром
распределение
полностью определяется параметром ![]() . Для
. Для ![]() имеем полунормальное
распределение, для
имеем полунормальное
распределение, для ![]() - распределение Рэлея,
для
- распределение Рэлея,
для ![]() - распределение Максвелла.
- распределение Максвелла.
В общем случае функция распределения
этого закона при четном и нечетном ![]() представляется
соответственно выражениями:
представляется
соответственно выражениями:
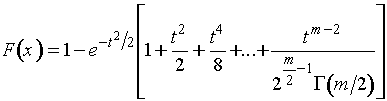
и
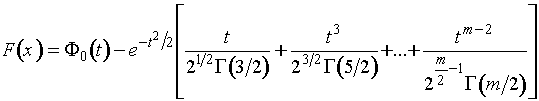
где
![]() ;
; 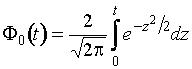 .
.
Информационное количество Фишера по
группированным наблюдениям определяется соотношением
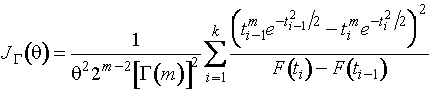 ,
,
а
для негруппированных - ![]() .
.
При ![]() для полунормального распределения
информационное количество Фишера по группированным данным описывается соотношением
для полунормального распределения
информационное количество Фишера по группированным данным описывается соотношением
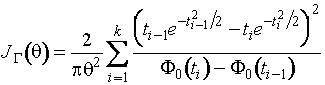 ,
,
по
негруппированным - ![]() .
.
Асимптотически оптимальные граничные точки
интервалов группирования в виде ![]() представлены в прил.
П1.6 вместе с соответствующими значениями
представлены в прил.
П1.6 вместе с соответствующими значениями ![]() . Оптимальные вероятности приведены в прил. П1.7.
. Оптимальные вероятности приведены в прил. П1.7.
Для ![]() функция плотности
примет вид
функция плотности
примет вид
![]() ,
,
функция
распределения
![]() ,
,
где
![]() . Информационное количество Фишера по группированным данным
о параметре
. Информационное количество Фишера по группированным данным
о параметре ![]() записывается в форме
записывается в форме
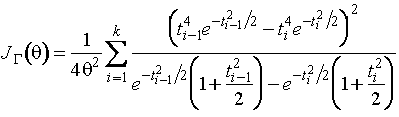 ,
,
где
![]() ; по негруппированным наблюдениям -
; по негруппированным наблюдениям - ![]() .
.
Асимптотически оптимальные граничные
точки, максимизирующие ![]() , представлены в прил. П1.8, соответствующие вероятности - в
прил. П1.9.
, представлены в прил. П1.8, соответствующие вероятности - в
прил. П1.9.
Решения задачи асимптотически
оптимального группирования при ![]() приведены в прил.
П1.10-П1.11, для
приведены в прил.
П1.10-П1.11, для ![]() - в прил. П1.12-П1.13,
для
- в прил. П1.12-П1.13,
для ![]() - в прил. П1.14-П1.15,
для
- в прил. П1.14-П1.15,
для ![]() - в прил. П1.16-П1.17,
для
- в прил. П1.16-П1.17,
для ![]() - в прил. П1.18-П1.19.
- в прил. П1.18-П1.19.
Функция плотности распределения Вейбулла (Вейбулла-Гнеденко) определяется двумя
параметрами: основным и масштабным. В прил. П1.20 приведены асимптотически
оптимальные граничные точки интервалов для оценивания основного параметра при
известном масштабном. Они максимизируют информационное количество Фишера о ![]() по группированным
данным
по группированным
данным
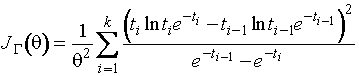 ,
,
где
![]() . Соответствующие вероятности даны в прил. П1.21. Информационное
количество Фишера по негруппированным данным о параметре
. Соответствующие вероятности даны в прил. П1.21. Информационное
количество Фишера по негруппированным данным о параметре ![]() определяется
соотношением
определяется
соотношением
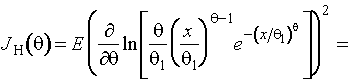
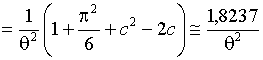 ,
,
где
![]() - постоянная Эйлера.
Значения относительной асимптотической информации
- постоянная Эйлера.
Значения относительной асимптотической информации ![]() представлены в этих же
приложениях.
представлены в этих же
приложениях.
Следует отметить, что задача
асимптотически оптимального группирования в данном случае оказалась
многоэкстремальной. В прил. П1.20 приведены значения граничных точек,
соответствующие глобальному экстремуму.
Информационное количество Фишера по
группированным наблюдениям о масштабном параметре ![]() при известном
параметре
при известном
параметре ![]() описываются
выражением
описываются
выражением
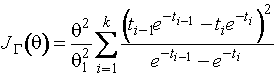 ,
,
где
![]() ; по негруппированным данным -
; по негруппированным данным -
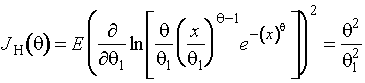 .
.
Асимптотически оптимальные граничные
точки в виде ![]() для оценивания
масштабного параметра
для оценивания
масштабного параметра ![]() и соответствующие
значения относительной асимптотической информации
и соответствующие
значения относительной асимптотической информации ![]() могут быть взяты из
прил. П1.1, значения вероятностей - из прил. П1.2. [62,29].
могут быть взяты из
прил. П1.1, значения вероятностей - из прил. П1.2. [62,29].
При одновременном оценивании двух
параметров распределения Вейбулла дисперсионная матрица оценки параметров
определяется информационной матрицей Фишера по группированным наблюдениям.
Эта матрица имеет вид
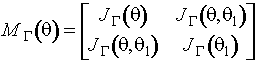 ,
,
где 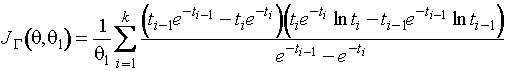 .
.
Информационная матрица Фишера по
негруппированным наблюдениям
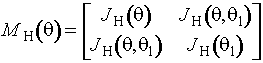 ,
,
где
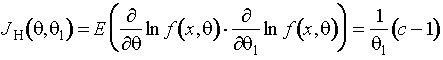 ,
, ![]() - постоянная
Эйлера. Асимптотически оптимальные граничные точки, максимизирующие
определитель матрицы
- постоянная
Эйлера. Асимптотически оптимальные граничные точки, максимизирующие
определитель матрицы ![]() , и соответствующие значения относительной асимптотической
информации
, и соответствующие значения относительной асимптотической
информации
![]()
![]()
представлены
в прил. П1.22, а соответствующие оптимальному группированию вероятности - в
прил. П1.23.
На рис. 2.2.2 показан выигрыш в
относительной асимптотической информации при использовании оптимального
группирования по сравнению с разбиением на интервалы равной вероятности для
распределения Вейбулла.
Информационное количество Фишера по
группированным данным о параметре ![]() нормального
распределения описывается выражением
нормального
распределения описывается выражением
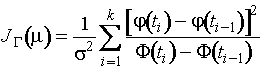 ,
,
где
![]() ;
; ![]() ;
; 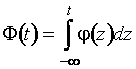 . Асимптотически оптимальные граничные точки, максимизирующие
. Асимптотически оптимальные граничные точки, максимизирующие
![]() , приведены в прил. П1.24. Здесь же приведены значения
относительной асимптотической информации
, приведены в прил. П1.24. Здесь же приведены значения
относительной асимптотической информации ![]() . Решение данной задачи впервые было дано в [65]. Вычисленные
значения соответствующих оптимальных вероятностей представлены в прил. П1.25.
. Решение данной задачи впервые было дано в [65]. Вычисленные
значения соответствующих оптимальных вероятностей представлены в прил. П1.25.
Для стандартного отклонения нормального
распределения информационное количество Фишера по группированным наблюдениям
равно
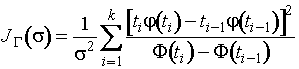
где ![]() . Асимптотически оптимальные граничные точки, максимизирующие
. Асимптотически оптимальные граничные точки, максимизирующие
![]() были получены в [65].
Эти значения проверены, исправлены при
были получены в [65].
Эти значения проверены, исправлены при ![]() и представлены в прил.
П1.26. Здесь же даны значения относительной асимптотической информации
и представлены в прил.
П1.26. Здесь же даны значения относительной асимптотической информации ![]() , где
, где ![]() - информационное
количество Фишера о
- информационное
количество Фишера о ![]() по негруппированным
данным. Соответствующие значения оптимальных вероятностей представлены в
прил. П1.27.
по негруппированным
данным. Соответствующие значения оптимальных вероятностей представлены в
прил. П1.27.
Асимптотически оптимальные граничные
точки интервалов, максимизирующие определитель информационной матрицы по
группированным данным,
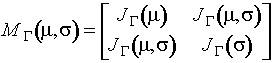 ,
,
где
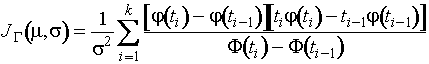 ,
,
в
форме ![]() даны в прил. П1.28.
Здесь же приведены соответствующие значения относительной асимптотической
информации
даны в прил. П1.28.
Здесь же приведены соответствующие значения относительной асимптотической
информации
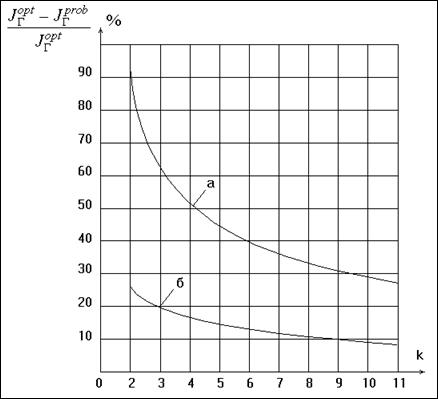
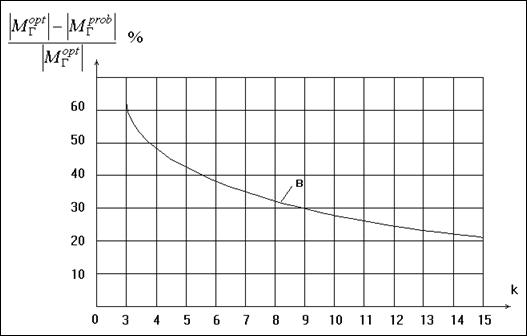
Рис. 2.2.2. Относительные потери в информационном
количестве Фишера при равновероятном группировании по сравнению с асимптотически
оптимальным группированием для распределения Вейбулла:
а - при
оценивании основного параметра;
б - при
оценивании масштабного параметра;
в - при оценивании двух параметров.
![]() ,
,
где
![]() - информационная
матрица параметров нормального распределения по негруппированнщй выборке
- информационная
матрица параметров нормального распределения по негруппированнщй выборке
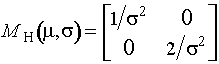 .
.
Значения оптимальных
вероятностей приведены в прил. П1.29.
Для логарифмически нормальных распределений асимптотически оптимальные
граничные точки для оценивания параметров ![]() ,
, ![]() или одновременно
или одновременно ![]() и
и ![]() (или для проверки
гипотез) соответственно те же самые, что и для нормального распределения, и
даны в прил. П1.24-П1.29. Но для распределения с плотностью
(или для проверки
гипотез) соответственно те же самые, что и для нормального распределения, и
даны в прил. П1.24-П1.29. Но для распределения с плотностью
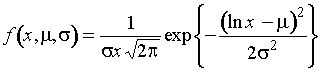
они
представлены там в виде ![]() , а для распределения с плотностью
, а для распределения с плотностью
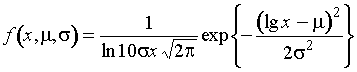
в
форме ![]() .
.
Приведенные на рис. 2.2.3 результаты
сравнения отражают степень предпочтительности оптимального группирования по
отношению к равновероятному для нормального закона распределения.
Информационное количество Фишера о
параметре ![]() распределения наибольшего экстремального значения описывается
выражением
распределения наибольшего экстремального значения описывается
выражением
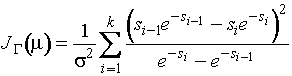 ,
,
где
![]() [69]. Асимптотически
оптимальные граничные точки, максимизирующие
[69]. Асимптотически
оптимальные граничные точки, максимизирующие ![]() , в виде
, в виде ![]() представлены в прил.
П1.30. В нем же приведены соответствующие значения относительной
асимптотической информации
представлены в прил.
П1.30. В нем же приведены соответствующие значения относительной
асимптотической информации ![]() , где
, где
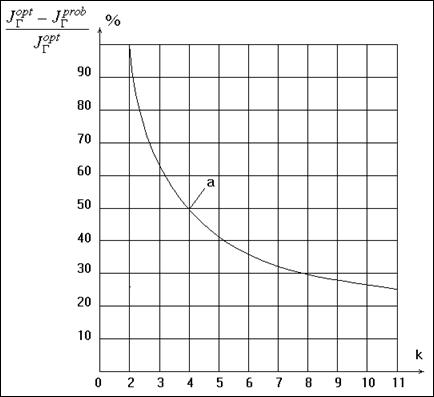
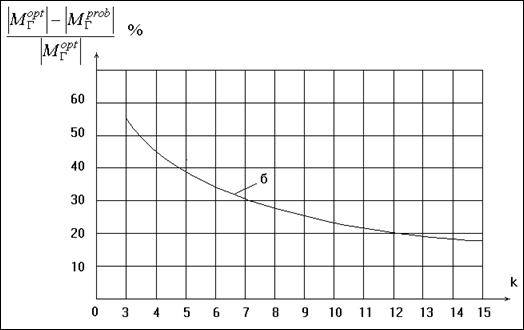
Рис. 2.2.3. Относительные потери в информационном
количестве Фишера при равновероятном группировании по сравнению с асимптотически
оптимальным группированием для нормального распределения
а
- при оценивании стандартного отклонения; б
- при оценивании математического ожидания и стандартного отклонения.
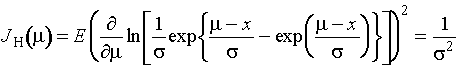
-
информационное количество по негруппированной выборке. Вероятности, соответствующие
оптимальному группированию, содержатся в прил. П1.31.
Информационное количество Фишера о
параметре ![]() распределения
наибольшего экстремального значения определяется соотношением
распределения
наибольшего экстремального значения определяется соотношением
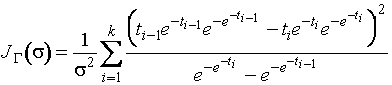 ,
,
где
![]() . Асимптотически оптимальные граничные точки, максимизирующие
. Асимптотически оптимальные граничные точки, максимизирующие
![]() , представлены в прил. П1.32 вместе с соответствующими
значениями относительной асимптотической информации
, представлены в прил. П1.32 вместе с соответствующими
значениями относительной асимптотической информации
![]() ,
,
где
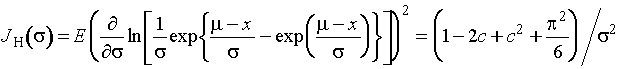 ;
;
![]() - постоянная Эйлера.
Значения оптимальных вероятностей приведены в прил. П1.33. В приложениях
приведены значения, соответствующие глобальному
экстремуму данной задачи асимптотически оптимального группирования, так как
она оказалась многоэкстремальной.
- постоянная Эйлера.
Значения оптимальных вероятностей приведены в прил. П1.33. В приложениях
приведены значения, соответствующие глобальному
экстремуму данной задачи асимптотически оптимального группирования, так как
она оказалась многоэкстремальной.
Вид информационной матрицы Фишера по
группированным наблюдениям для параметров распределения наибольшего
экстремального значения определяется выражением
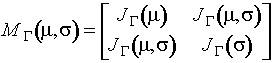 ,
,
где
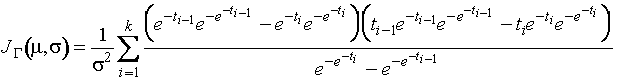 ;
;
![]() . Информационная матрица по негруппированным данным
. Информационная матрица по негруппированным данным
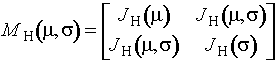 ,
,
где
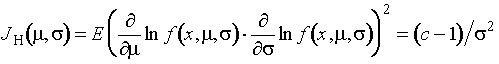 ;
; ![]() - постоянная Эйлера.
Асимптотически оптимальные граничные точки в виде
- постоянная Эйлера.
Асимптотически оптимальные граничные точки в виде ![]() , максимизирующие определитель матрицы
, максимизирующие определитель матрицы ![]() , представлены в прил. П1.34. Здесь же даны значения
относительной асимптотической информации в виде соотношения
, представлены в прил. П1.34. Здесь же даны значения
относительной асимптотической информации в виде соотношения
![]() .
.
В
прил. П1.35 показаны полученные оптимальные вероятности.
Выражение для информационного
количества Фишера о параметре ![]() распределения наименьшего
экстремального значения по группированной выборке имеет вид
распределения наименьшего
экстремального значения по группированной выборке имеет вид
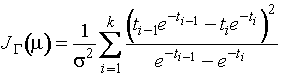 ,
,
где
![]() . В таком виде асимптотически оптимальные граничные точки,
максимизирующие
. В таком виде асимптотически оптимальные граничные точки,
максимизирующие ![]() , представлены в прил. П1.1, а соответствующие вероятности в
прил. П1.2.
, представлены в прил. П1.1, а соответствующие вероятности в
прил. П1.2.
Информационное количество о параметре ![]() имеет вид
имеет вид
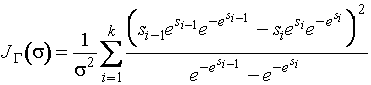 ,
,
где
![]() . Оптимальные граничные точки для этого случая представлены в
прил. П1.20 в виде
. Оптимальные граничные точки для этого случая представлены в
прил. П1.20 в виде ![]() , а соответствующие вероятности - в прил. П1.21.
, а соответствующие вероятности - в прил. П1.21.
Информационная матрица Фишера
параметров распределения наименьшего значения
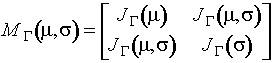 ,
,
где
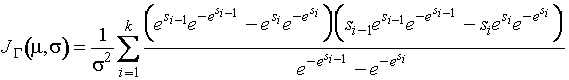
для
![]() . Информационная матрица по негруппированным данным
совпадает с информационной матрицей Фишера для распределения наибольшего
значения. Асимптотически оптимальные граничные точки, максимизирующие
определитель
. Информационная матрица по негруппированным данным
совпадает с информационной матрицей Фишера для распределения наибольшего
значения. Асимптотически оптимальные граничные точки, максимизирующие
определитель ![]() , в виде
, в виде ![]() представлены в
прил.П1.22, а оптимальные вероятности - в прил. П1.23.
представлены в
прил.П1.22, а оптимальные вероятности - в прил. П1.23.
Решение задачи асимптотически
оптимального группирования для распределения
Коши рассматривалось в [39]. Информационное количество Фишера по
группированным наблюдениям о масштабном параметре ![]() распределения Коши
описывается соотношением
распределения Коши
описывается соотношением
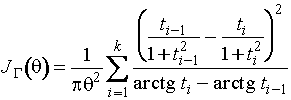 ,
,
где
![]() . Полученные асимптотически оптимальные граничные точки,
максимизирующие
. Полученные асимптотически оптимальные граничные точки,
максимизирующие ![]() , представлены в прил. П1.36. В нем же приведены значения
относительной асимптотической информации
, представлены в прил. П1.36. В нем же приведены значения
относительной асимптотической информации ![]() , позволяющие судить о качестве группирования и величине
потерь информации, связанных с группированием выборки. Информационное
количество Фишера по негруппированной выборке определяется выражением
, позволяющие судить о качестве группирования и величине
потерь информации, связанных с группированием выборки. Информационное
количество Фишера по негруппированной выборке определяется выражением
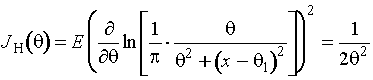 .
.
Значения
оптимальных вероятностей, соответствующих рассматриваемому случаю, представлены
в прил. П1.37.
Информационное количество о параметре ![]() распределения Коши по
группированной выборке
распределения Коши по
группированной выборке
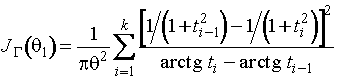 ,
,
где
![]() . По негруппированным данным информационное количество
Фишера определяется выражением
. По негруппированным данным информационное количество
Фишера определяется выражением
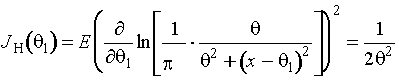 .
.
Асимптотически
оптимальные граничные точки, максимизирующие ![]() , также получены и представлены в прил. П1.38. Здесь же даны
значения относительной асимптотической информации
, также получены и представлены в прил. П1.38. Здесь же даны
значения относительной асимптотической информации ![]() . Соответствующие значения оптимальных частот приведены в
прил. П1.39.
. Соответствующие значения оптимальных частот приведены в
прил. П1.39.
Информационная матрица Фишера
параметров распределения Коши по группированным наблюдениям
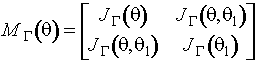
где 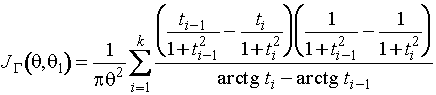 для
для 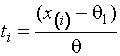 . Асимптотически оптимальные групповые пределы,
максимизирующие определитель матрицы
. Асимптотически оптимальные групповые пределы,
максимизирующие определитель матрицы ![]() , представлены в прил. П1.40. Для сравнения со случаем
негруппированной выборки в этом же приложении приведены значения относительной
асимптотической информации
, представлены в прил. П1.40. Для сравнения со случаем
негруппированной выборки в этом же приложении приведены значения относительной
асимптотической информации ![]() , где определитель информационной матрицы по негруппированным
наблюдениям
, где определитель информационной матрицы по негруппированным
наблюдениям ![]() .
.
В отличие от всех ранее рассмотренных
случаев оптимальное группирование относительно двух параметров распредления
Коши разбивает область определения случайной величины на интервал, которым
соответствуют равные вероятности.
Информационное количество Фишера о
параметре ![]() логистического распределения по группированной выборке определяется
выражением
логистического распределения по группированной выборке определяется
выражением
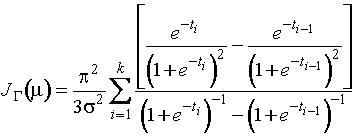 ,
,
где
![]() . Максимизирующие его оптимальные граничные точки приведены в
прил. П1.41. Информационное количество по негруппированным наблюдениям
. Максимизирующие его оптимальные граничные точки приведены в
прил. П1.41. Информационное количество по негруппированным наблюдениям
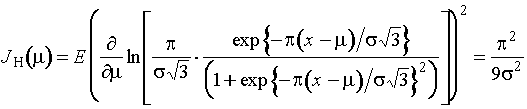 .
.
Кроме
граничных точек в прил. П1.41 представлены значения относительной
асимптотической информации ![]() , позволяющие судить о потерях информации, связанных с
группированием наблюдений. Соответствующие значения вероятностей оказались
равны: оптимальное группирование совпало с разбиением на интервалы равной вероятности.
, позволяющие судить о потерях информации, связанных с
группированием наблюдений. Соответствующие значения вероятностей оказались
равны: оптимальное группирование совпало с разбиением на интервалы равной вероятности.
Информационное количество Фишера о
параметре ![]() логистического
распределения по группированной выборке имеет вид
логистического
распределения по группированной выборке имеет вид
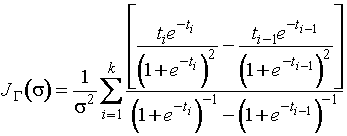 ,
,
а
по негруппированным наблюдениям
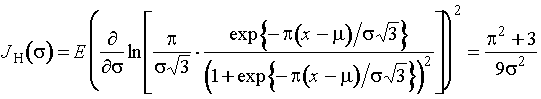 .
.
Значения
асимптотически оптимальных граничных точек, максимизирующих ![]() , и значения относительной асимптотической информации
, и значения относительной асимптотической информации ![]() представлены в прил.
П1.42, а значения соответствующих вероятностей - в прил. П1.43.
представлены в прил.
П1.42, а значения соответствующих вероятностей - в прил. П1.43.
Информационная матрица Фишера по
группированным наблюдениям о параметрах логистического распределения
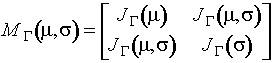 ,
,
где
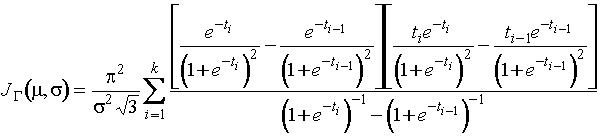 ,
,
а
информационная матрица по негруппированным данным
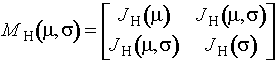 ,
,
где
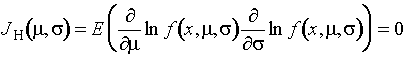 .
.
Асимптотически оптимальные граничные
точки и соответствующие значения ![]() относительной
асимптотической информации представлены в прил. П1.44, а оптимальные значения
вероятностей попадания в интервалы - в прил. П1.45.
относительной
асимптотической информации представлены в прил. П1.44, а оптимальные значения
вероятностей попадания в интервалы - в прил. П1.45.
Информационное
количество Фишера по группированным данным о параметре ![]() гамма-распределения
определяется соотношением
гамма-распределения
определяется соотношением
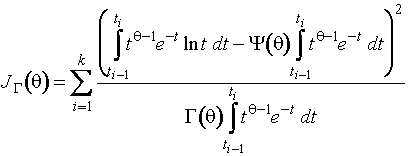 ,
,
где
![]() . В таком виде оптимальные граничные точки в зависимости от
значения основного параметра
. В таком виде оптимальные граничные точки в зависимости от
значения основного параметра ![]() (формы) представлены в
прил. П1.53. Для сравнения с негруппированным случаем здесь же приведены
значения относительной асимптотической информации
(формы) представлены в
прил. П1.53. Для сравнения с негруппированным случаем здесь же приведены
значения относительной асимптотической информации ![]() , где информационное количество по негруппированным данным
, где информационное количество по негруппированным данным ![]() . Эта задача впервые решалась в [31].
. Эта задача впервые решалась в [31].
В случае гамма-распределения решение
задачи оптимального группирования не может быть получено в виде инвариантном
относительно параметров распределения. Оптимальные граничные точки являются
функциями параметра ![]() . В принципе, граничные точки при значениях
. В принципе, граничные точки при значениях ![]() , не совпадающих с приводимыми в прил. П1.53, могут быть
получены с помощью интерполяции. Это затрудняет использование готового решения
в различных постановках задачи оценивания неизвестных параметров
гамма-распределения, делает весьма проблематичной ее необходимость. Но по
отношению к критериям согласия актуальность использования асимптотически
оптимального группирования сохраняется.
, не совпадающих с приводимыми в прил. П1.53, могут быть
получены с помощью интерполяции. Это затрудняет использование готового решения
в различных постановках задачи оценивания неизвестных параметров
гамма-распределения, делает весьма проблематичной ее необходимость. Но по
отношению к критериям согласия актуальность использования асимптотически
оптимального группирования сохраняется.
Для масштабного параметра ![]() информационное
количество по группированным данным находится из выражения
информационное
количество по группированным данным находится из выражения
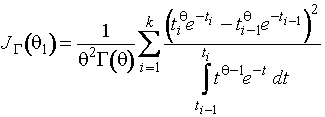 ,
,
где
![]() ;
; ![]() - гамма-функция
Эйлера. Информационное количество по негруппированным выборкам -
- гамма-функция
Эйлера. Информационное количество по негруппированным выборкам -
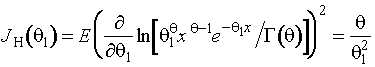 .
.
Эта
задача решалась в работе [37]. Асимптотически оптимальные граничные точки в
виде ![]() в зависимости от
основного параметра
в зависимости от
основного параметра ![]() представлены в прил.
П1.54. В нем же для сравнения с негруппированной выборкой приведены значения
относительной асимптотической информации
представлены в прил.
П1.54. В нем же для сравнения с негруппированной выборкой приведены значения
относительной асимптотической информации ![]() .
.
Информационное
количество Фишера по группированным данным о параметре ![]() распределения Парето дается соотношением
распределения Парето дается соотношением
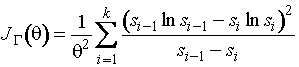 ,
,
где
![]() ;
; ![]() - параметр сдвига
распределения. По негруппированной выборке информационное количество о
параметре
- параметр сдвига
распределения. По негруппированной выборке информационное количество о
параметре ![]() имеет вид
имеет вид
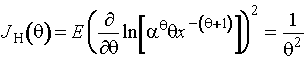 .
.
Асимптотически
оптимальные граничные точки в виде ![]() и соответствующие
значения
и соответствующие
значения ![]() содержатся в прил.
П1.1, а оптимальные вероятности - в прил. П1.2.
содержатся в прил.
П1.1, а оптимальные вероятности - в прил. П1.2.
Количество информации Фишера о
параметре распределения Лапласа по
группированным наблюдениям определяется выражением
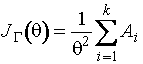 ,
,
где
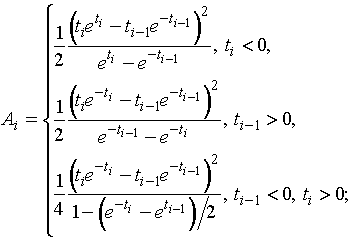
и ![]() . Количество информации Фишера по негруппированным наблюдениям
определяется величиной
. Количество информации Фишера по негруппированным наблюдениям
определяется величиной
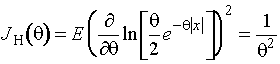 .
.
Решение
данной задачи оптимального группирования представлено в прил. П1.46, П1.47, П1.48, П1.49.
Функция плотности двойного
показательного распределения
![]() ,
,
где
![]() ;
; ![]() , определяется двумя параметрами. Вероятность попадания
наблюдения в интервал значений
, определяется двумя параметрами. Вероятность попадания
наблюдения в интервал значений
![]() ,
,
где
![]() . Информационное количество Фишера о параметре
. Информационное количество Фишера о параметре ![]() по группированным
наблюдениям имеет вид
по группированным
наблюдениям имеет вид
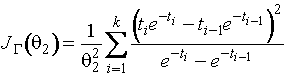 ,
,
а
по негруппированным - ![]() .
.
При решении задачи асимптотически оптимального
группирования для параметра ![]() максимизировалась
относительная асимптотичекая информация
максимизировалась
относительная асимптотичекая информация ![]() . Соответствующие асимптотически оптимальные граничные точки
представлены в прил. П1.1 в виде
. Соответствующие асимптотически оптимальные граничные точки
представлены в прил. П1.1 в виде ![]() вместе со значениями
вместе со значениями ![]() , а вероятности попадания в интервал в прил. П1.31.
, а вероятности попадания в интервал в прил. П1.31.
Информационное количество Фишера о параметре ![]() по группированным
данным при
по группированным
данным при ![]() -
-
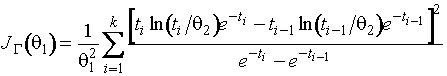 ,
,
а
по негруппированным -
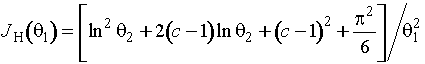 ,
,
где
![]() - постоянная Эйлера.
Относительная асимптотическая информация
- постоянная Эйлера.
Относительная асимптотическая информация ![]() в данном случае зависит от
в данном случае зависит от ![]() . Решения задачи асимптотически оптимального группирования
получено при различных значениях
. Решения задачи асимптотически оптимального группирования
получено при различных значениях ![]() и представлены в прил.
П1.50, а соответствующие вероятности в прил. П1.51.
и представлены в прил.
П1.50, а соответствующие вероятности в прил. П1.51.
При одновременном оценивании двух параметров
распределения рассматривается информационная матрица Фишера по группированным
данным
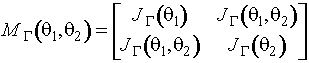 ,
,
где
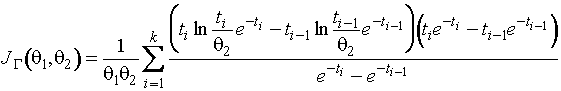 .
.
Информационная матрица Фишера по
негруппированным наблюдениям -
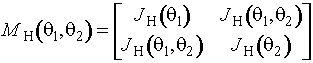 ,
,
где
![]() .
.
При решении задачи асимптотически
оптимального группирования максимизировалась величина ![]() , причем определитель информационной матрицы по
негруппированным данным
, причем определитель информационной матрицы по
негруппированным данным 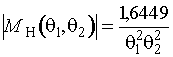 . Решение задачи приведено в прил. П1.52, а соответствующие
вероятности - в прил. П1.35. Подчеркнем, что это решение
. Решение задачи приведено в прил. П1.52, а соответствующие
вероятности - в прил. П1.35. Подчеркнем, что это решение
получается
в виде инвариантном относительно параметров распределения: граничные точки в
таблице не зависят от ![]() .
.
Выводы
Таким
образом, для широкого ряда распределений при решении задач асимптотически
оптимального группирования удалось получить граничные точки интервалов в
виде, инвариантном относительно параметров распределений и на их основе
сформировать таблицы асимптотически оптимального группирования. В
совокупности были получены таблицы для распределений экспоненциального,
полунормального, Рэлея, Максвелла, модуля многомерного нормального
вектора, Парето, Эрланга, Лапласа, нормального, логарифмически-нормальных (ln
и lg), Коши, Вейбулла, распределений минимального и максимального значения,
двойного показательного, гамма-распределения. В общей сложности, 54 таблицы
оптимальных граничных точек и соответствующих вероятностей, которые
приведены в приложении П1.
2.3. О возможности практического использования асимптотически оптимального группирования в задачах оценивания параметров
Возможность эффективного использования
оптимального группирования при оценивании параметров распределений в первый момент
всегда вызывает сомнения.
Первое возражение связано с доводом, а
зачем вообще группировать наблюдения и терять информацию? Cовременный уровень
вычислительной техники и запоминающих устройств для хранения информации
позволяют не думать о группировании, как способе сжатия данных или ускорения
вычислений при оценивании параметров. Всё справедливо, если эти наблюдения
принадлежат действительно тому закону, параметры которого мы оцениваем. Но если
наблюдаемая выборка содержит отклонения от наших предположений, то это может
существенно отразиться на получаемых оценках. В главе 3 предлагается для
вычисления робастных оценок максимального правдоподобия использовать предварительное
группирование наблюдений и вычислять ОМП уже по группированным данным. Это позволяет
получать оценки, устойчивые к наличию аномальных наблюдений или другим
отклонениям от предположений. И использование асимптотически оптимального
группирования в этом случае приносит положительные результаты. С другой
стороны, в случае больших выборок вычисление ОМП по группированным данным
оказывается экономичней по сравнению с поиском оценок непосредственно по
несгруппированным данным. Далее, давно известно, что оценки параметров,
вычисляемые по выборочным квантилям также являются робастными. Предлагаемые
нами оценки, использующие выборочные квантили, соответствующие асимптотически
оптимальному группированию, рассматриваются в последующих разделах данной
главы.
Второе возражение определяется тем, что
истинные значения оцениваемых параметров нам неизвестны, а асимптотически
оптимальные граничные точки зависят от параметров. Как же группировать? Если в
нашем распоряжении выборка, состоящая из индивидуальных наблюдений, и к
группированию мы прибегаем для того, чтобы получить робастные ОМП по
группированным данным, то разбивая выборку на интервалы мы должны
воспользоваться таблицами оптимальных вероятностей, разделяя выборку на части,
пропорциональные им. Если же группирование вызвано технологическими причинами и
возможна фиксация только принадлежности наблюдения некоторому интервалу
значений, то выбор граничных точек возможен по прогнозируемым значениям
параметров. В большинстве практических ситуаций имеются некоторые априорные
сведения о параметрах закона. В таком случае существует возможность выбора
оптимальных граничных точек (шкалирование) относительно прогнозируемого
значения параметра. Эти априорные сведения могут поступать от предыдущих экспериментов
или следовать из теоретических или практических предпосылок.
Конечно, используемые априорные
сведения о параметре могут существенно отличаться от его истинного значения. Тогда оптимальное группирование по
прогнозируемому значению параметра приводит к потере в относительной
асимптотической информации. В этом случае интересно знать, при каких ошибках
прогноза имеет смысл проводить оптимальное группирование по априорным
сведениям о параметре.
Величина потерь в относительной
асимптотической информации может быть рассчитана [32,36]. Например, выражение
для потерь в относительной асимптотической информации для оценки
математического ожидания нормального распределения имеет вид
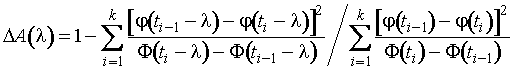 ,
,
где
![]() - оптимальные
граничные точки по ошибочному прогнозу;
- оптимальные
граничные точки по ошибочному прогнозу;
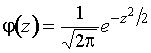 ;
; 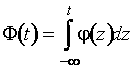 .
.
Вычисленные
значения потерь в зависимости от ошибки прогнозирования ![]() и оцениваемого
параметра
и оцениваемого
параметра ![]() представлены в табл.
2.3.1.
представлены в табл.
2.3.1.
Таблица 2.3.1
Потери в относительной асимптотической информации при
оценивании математического ожидания нормального распределения по группированным
данным вследствие ошибочного прогноза, %
|
|
|
||||||||
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2,0 |
79,40 |
61,53 |
48,76 |
39,64 |
32,95 |
27,89 |
23,27 |
20,86 |
18,35 |
|
1,9 |
75,75 |
57,11 |
44,43 |
35,63 |
29,30 |
24,59 |
20,98 |
18,14 |
15,87 |
|
1,8 |
71,75 |
52,57 |
40,14 |
31,76 |
25,85 |
21,51 |
18,22 |
15,66 |
13,63 |
|
1,7 |
67,37 |
47,97 |
35,96 |
28,07 |
22,61 |
18,66 |
15,70 |
13,41 |
11,61 |
|
1,6 |
62,69 |
43,35 |
31,91 |
24,59 |
19,61 |
16,05 |
13,41 |
11,39 |
9,81 |
|
1,5 |
57,73 |
38,78 |
28,03 |
21,32 |
16,84 |
13,67 |
11,35 |
9,59 |
8,22 |
|
1,4 |
52,56 |
34,29 |
24,35 |
18,30 |
14,31 |
11,53 |
9,51 |
7,80 |
6,82 |
|
1,3 |
47,24 |
29,95 |
20,90 |
15,52 |
12,03 |
9,62 |
7,89 |
6,60 |
5,61 |
|
1,2 |
41,83 |
25,79 |
17,70 |
12,99 |
9,98 |
7,93 |
6,47 |
5,38 |
4,55 |
|
1,1 |
36,42 |
21,87 |
14,77 |
10,72 |
8,17 |
6,45 |
5,23 |
4,33 |
3,65 |
|
1,0 |
31,10 |
18,19 |
12,11 |
8,70 |
6,58 |
5,16 |
4,17 |
3,44 |
2,89 |
|
0,9 |
15,95 |
14,81 |
9,72 |
6,92 |
5,19 |
4,05 |
3,26 |
2,68 |
2,24 |
|
0,8 |
21,05 |
11,75 |
7,61 |
5,37 |
4,01 |
3,11 |
2,49 |
2,04 |
1,70 |
|
0,7 |
16,50 |
9,02 |
5,78 |
4,04 |
3,00 |
2,32 |
1,85 |
1,51 |
1,25 |
|
0,6 |
12,37 |
6,64 |
4,21 |
2,92 |
2,16 |
1,66 |
1,32 |
1,07 |
0,89 |
|
0,5 |
8,74 |
4,62 |
2,90 |
2,00 |
1,47 |
1,13 |
0,89 |
0,89 |
0,60 |
|
0,4 |
5,67 |
2,96 |
1,84 |
1,27 |
0,93 |
0,71 |
0,56 |
0,45 |
0,38 |
|
0,3 |
3,22 |
1,66 |
1,03 |
0,71 |
0,51 |
0,39 |
0,31 |
0,25 |
0,21 |
|
0,2 |
1,44 |
0,74 |
0,46 |
0,31 |
0,22 |
0,17 |
0,14 |
0,11 |
0,09 |
|
0,1 |
0,36 |
0,18 |
0,11 |
0,08 |
0,06 |
0,04 |
0,03 |
0,03 |
0,02 |
Потери в относительной асимптотической
информации при оценивании среднеквадратичного отклонения вследствие
ошибочного прогноза при известном математическом ожидании определяется
соотношением
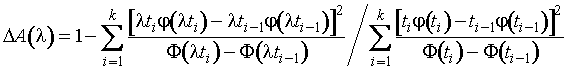 .
.
Оптимальные
граничные точки по ошибочному прогнозу в данном случае имеют вид ![]() , где
, где ![]() - известное
математическое ожидание;
- известное
математическое ожидание; ![]() - предполагаемое
значение стандартного отклонения. Величины потерь в зависимости от
- предполагаемое
значение стандартного отклонения. Величины потерь в зависимости от ![]() представлены в табл.
2.3.2.
представлены в табл.
2.3.2.
Таблица 2.3.2
Потери в относительной асимптотической информации при
оценивании стандартного отклонения нормального распределения по группированным
данным вследствие ошибочного прогноза, %
|
|
|
||||||||
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0,1 |
97,43 |
89,91 |
89,31 |
88,90 |
88,38 |
87,92 |
87,48 |
87,07 |
86,70 |
|
0,2 |
89,99 |
78,03 |
76,50 |
75,46 |
74,22 |
73,12 |
72,10 |
71,14 |
70,28 |
|
0,3 |
73,47 |
64,89 |
62,42 |
60,71 |
58,81 |
57,12 |
55,61 |
54,17 |
62,93 |
|
0,4 |
64,10 |
51,17 |
48,05 |
45,26 |
43,59 |
41,56 |
39,80 |
38,14 |
36,74 |
|
0,5 |
48,39 |
37,67 |
34,40 |
32,07 |
29,82 |
27,80 |
26,13 |
24,54 |
23,26 |
|
0,6 |
32,95 |
25,24 |
22,35 |
27,27 |
18,40 |
16,71 |
15,39 |
14,14 |
13,16 |
|
0,7 |
19,31 |
14,67 |
12,58 |
11,06 |
9,79 |
8,65 |
7,80 |
6,99 |
6,40 |
|
0,8 |
8,77 |
6,44 |
5,52 |
4,69 |
4,06 |
3,48 |
3,08 |
2,69 |
2,42 |
|
0,9 |
2,20 |
1,67 |
1,35 |
1,10 |
0,98 |
0,78 |
0,68 |
0,58 |
0,81 |
|
1,0 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
1,1 |
2,09 |
1,62 |
1,24 |
0,96 |
0,78 |
0,62 |
0,52 |
0,43 |
0,38 |
|
1,2 |
7,33 |
6,26 |
4,42 |
3,51 |
2,84 |
2,22 |
1,87 |
1,53 |
1,32 |
|
1,3 |
16,69 |
13,41 |
10,02 |
7,27 |
5,86 |
4,53 |
3,80 |
3,09 |
2,65 |
|
1,4 |
27,34 |
22,42 |
16,68 |
11,93 |
9,59 |
7,38 |
6,18 |
5,01 |
4,30 |
|
1,5 |
38,84 |
32,54 |
24,28 |
17,26 |
13,88 |
10,69 |
8,95 |
7,25 |
6,24 |
|
1,6 |
50,28 |
43,05 |
32,41 |
23,10 |
18,64 |
14,40 |
12,08 |
9,81 |
8,45 |
|
1,7 |
60,92 |
53,31 |
40,71 |
29,35 |
23,81 |
18,49 |
15,55 |
12,68 |
10,93 |
|
1,8 |
70,28 |
62,82 |
48,88 |
35,89 |
29,31 |
22,93 |
19,35 |
15,83 |
13,68 |
|
1,9 |
78,11 |
71,22 |
56,65 |
42,60 |
35,07 |
27,67 |
23,44 |
19,27 |
16,69 |
|
2,0 |
84,39 |
78,35 |
63,84 |
49,36 |
40,99 |
32,67 |
27,80 |
22,97 |
19,95 |
|
2,1 |
89,21 |
84,16 |
70,33 |
55,98 |
46,97 |
37,85 |
32,37 |
26,90 |
23,43 |
Приводимые в таблицах результаты
вычислений позволяют сделать вывод, что при умеренных ошибках прогноза о
значении оцениваемого параметра потери в относительной асимптотической
информации, а, следовательно, и потери в информации, вызываемые группированием
наблюдений, имеют относительно малые величины при малых ошибках прогноза, особенно
при росте числа интервалов группирования.
Иногда при группировании пользуются
равноотстоящими граничными точками. При таком группировании представляет
интерес оптимальная длина интервала. В табл. 2.3.3. приведены оптимальные длины
интервалов при равноотстоящем группировании в виде ![]() для распределений
Рэлея и Максвелла, и в форме
для распределений
Рэлея и Максвелла, и в форме ![]() для распределения Вейбулла,
а также соответствующие значения относительной асимптотической информации
для распределения Вейбулла,
а также соответствующие значения относительной асимптотической информации ![]() . Если сравнить достигнутые значения
. Если сравнить достигнутые значения ![]() со значениями, соответствующими
асимптотически оптимальному группированию, то видно, что и такой способ
группирования имеет определенный смысл.
со значениями, соответствующими
асимптотически оптимальному группированию, то видно, что и такой способ
группирования имеет определенный смысл.
Таблица 2.3.3
Оптимальные длины интервалов группирования для
оценивания параметров распределениий Рэлея, Максвелла, Вейбулла
|
Распределения |
||||||
|
|
Рэлея |
Максвелла |
Вейбулла |
|||
|
|
|
|
|
|
|
|
|
2 |
1,7853 |
0,6476 |
2,0451 |
0,6451 |
1,5936 |
0,6476 |
|
3 |
1,1288 |
0,7808 |
1,2199 |
0,7639 |
1,2070 |
0,8076 |
|
4 |
0,8510 |
0,8696 |
0,9179 |
0,8529 |
0,9898 |
0,8749 |
|
5 |
0,6894 |
0,9113 |
0,7421 |
0,9000 |
0,8474 |
0,9105 |
|
6 |
0,5827 |
0,9357 |
0,6255 |
0,9276 |
0,7456 |
0,9320 |
|
7 |
0,5063 |
0,9517 |
0,5422 |
0,9451 |
0,6687 |
0,9461 |
|
8 |
0,4484 |
0,9616 |
0,4805 |
0,9568 |
0,6080 |
0,9560 |
|
9 |
0,4080 |
0,9689 |
0,4305 |
0,9651 |
0,5588 |
0,9632 |
|
10 |
0,3664 |
0,9743 |
0,3910 |
0,9713 |
0,5180 |
0,9687 |
Таким образом, можно выделить следующие
моменты, когда применение асимптотически оптимального группирования может дать
положительный эффект в задачах точечного оценивания параметров.