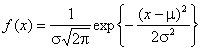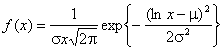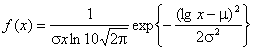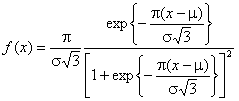Построение оптимальных L-оценок параметров сдвига и масштаба по выборочным асимптотически оптимальным квантилям

L-оценки параметров сдвига m и масштаба s используются в тех случаях, когда закон распределения полностью определяется только этими параметрами с функцией распределения F[(x-m)/s] и функцией плотности f[(x-m)/s]/s .

L-оценки параметров распределений, формируемые как линейные комбинации порядковых статистик или выборочных квантилей, обладают двумя важными для широкого практического применения качествами: чрезвычайной простотой вычислений и очень хорошими свойствами робастности. Самой сложной операцией при вычислении таких оценок является сортировка имеющейся выборки по возрастанию (формирование вариационного ряда) с целью определения выборочных квантилей наблюдаемого закона. Значения выборочных квантилей x_(i) находятся при разбиении области определения случайной величины (размаха выборки) на интервалы, величины которых пропорциональны вероятностям P_i попадания в интервал при асимптотически оптимальном группировании: число попаданий в интервал выбирается равным nP_i, где n - объем выборки. Подробнее с формированием оценок можно познакомиться в работе, опубликованной в Сибирском журнале индустриальной математики. (2001. - Т.4. - № 2. - С. 166-183.), и в работе, опубликованной журналом “Заводская лаборатория. Диагностика материалов”, где проведено дополнительное исследование свойств этих оценок. Там же приводятся ссылки на первоисточники.

Оценивание неизвестного m при известном s осуществляется по формуле

m = a ₀s + a ₁x₍₁₎ + a ₂x₍₂₎ + ... + a _k-1x_(k-1) .  (1)

Оценивание неизвестного s при известном m осуществляется по формуле

s = b ₀m + b ₁x₍₁₎ + b ₂x₍₂₎ + ... + b _k-1x_(k-1) . (2)

При оценивании сразу двух параметров используются соотношения:

m = g ₁x₍₁₎ + g ₂x₍₂₎ + ... + g _k-1x_(k-1),                                                                   (3)

s = n ₁x₍₁₎ + n ₂x₍₂₎ + ... + n _k-1x_(k-1). (4)

 Значения x_(i), фигурирующие в формулах (1), (2, (3) и (4), следует выбирать из условия

,

где X_(i) - члены вариационного ряда X₍₁₎ ≤ X₍₂₎ ≤ … ≤ X_(n), построенного по исходной выборке, , [.] - означает целую часть числа, а P_j - выбираются из соответствующей строки таблицы оптимальных вероятностей приложения А. Например, в качестве x_(i) могут быть взяты средние значения между соответствующими соседними членами вариационного ряда.

Значения коэффициентов для формул (1), (2), (3) и (4), соответствующие конкретным законам распределений, выбираются из таблиц приложения П.

Указания на используемые таблицы оптимальных вероятностей и таблицы коэффициентов a _i, b _i, g _i, n _i содержатся в нижеприведенной таблице 1.

Таблица 1. Указания на используемые таблицы оптимальных вероятностей и таблицы с коэффициентами для вычисления L-оценок

Распределение	Оцениваемый параметр	№ формулы	Таблица вероятностей	Таблица коэффициентов
Нормальное	m (известно s ) s (известно m ) m s	1 2 3 4	А.25 А.27 А.29 А.29	П.1 П.2 П.3 П.4
Логарифмически нормальное (ln)[1]	m (известно s ) s (известно m ) m s	1 2 3 4	А.25 А.27 А.29 А.29	П.1 П.2 П.3 П.4
Логарифмически нормальное (lg)[2]	m (известно s ) s (известно m ) m s	1 2 3 4	А.25 А.27 А.29 А.29	П.1 П.2 П.3 П.4
Логистическое	m (известно s ) s (известно m ) m s	1 2 3 4	Равновероятные А.43 А.45 А.45	П.5 П.6 П.7 П.8
Коши	m (известно s ) s (известно m ) m s	1 2 3 4	А.39 А.37 Равновероятные Равновероятные	П.9 П.10 П.11 П.12
Минимального значения	m (известно s ) s (известно m ) m s	1 2 3 4	А.2 А.21 А.23 А.23	П.13 П.14 П.15 П.16
Максимального значения	m (известно s ) s (известно m ) m s	1 2 3 4	А.31 А.33 А.35 А.35	П.17 П.18 П.19 П.20
Экспоненциальное (показательное)	m (известно s ) s (известно m ) m s	1 2 3 4	А.2 А.2 А.2 А.2	П.21 П.22 П.23 П.24
Модуля многомерного нормального вектора (m=1, полунормальное)	m (известно s ) s (известно m ) m s	1 2 3 4	А.7 А.7 А.7 А.7	П.25 П.26 П.27 П.28
Модуля многомерного нормального вектора (m=2, Рэлея)	m (известно s ) s (известно m ) m s	1 2 3 4	А.2 А.2 А.2 А.2	П.29 П.30 П.31 П.32
Модуля многомерного нормального вектора (m=3, Максвелла)	m (известно s ) s (известно m ) m s	1 2 3 4	А.5 А.5 А.5 А.5	П.33 П.34 П.35 П.36
Модуля многомерного нормального вектора (m=4)	m (известно s ) s (известно m ) m s	1 2 3 4	А.9 А.9 А.9 А.9	П.37 П.38 П.39 П.40
Модуля многомерного нормального вектора (m=5)	m (известно s ) s (известно m ) m s	1 2 3 4	А.11 А.11 А.11 А.11	П.41 П.42 П.43 П.44
Модуля многомерного нормального вектора (m=6)	m (известно s ) s (известно m ) m s	1 2 3 4	А.13 А.13 А.13 А.13	П.45 П.46 П.47 П.48
Модуля многомерного нормального вектора (m=7)	m (известно s ) s (известно m ) m s	1 2 3 4	А.15 А.15 А.15 А.15	П.49 П.50 П.51 П.52
Модуля многомерного нормального вектора (m=8)	m (известно s ) s (известно m ) m s	1 2 3 4	А.17 А.17 А.17 А.17	П.53 П.54 П.55 П.56
Модуля многомерного нормального вектора (m=9)	m (известно s ) s (известно m ) m s	1 2 3 4	А.19 А.19 А.19 А.19	П.57 П.58 П.59 П.60
Лапласа[3]	m (известно s ) s (известно m ) m s	1 2 3 4	А.48 А.48 А.48 А.48	П.61 П.62 П.63 П.64

[Гл. меню]

---

[1] В формулах (1)-(4) заменяется на .

[2] В формулах (1)-(4) заменяется на .

[3] Коэффициенты в таблицах П.61-П.64 соответствуют первому варианту (первой строке) оптимальных вероятностей из таблицы А.48 при соответствующем .