См. также: Прикладная математическая статистика (материалы к семинарам)

КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ О МАТЕМАТИЧЕСКИХ ОЖИДАНИЯХ

Б.Ю. Лемешко, Е.П. Миркин, М.А. Герасимов

Новосибирский государственный технический университет

Тел. сл. (383) 346-37-54. E-mail: headrd@fpm.ami.nstu.ru

Аннотация. Исследованы распределения параметрических критериев проверки гипотез об однородности математических ожиданий при нарушении предположений о нормальности. Исследована сходимость к предельным распределений статистик непараметрических критериев. Проведено сравнение мощности критериев.

Постановка задачи

В различных приложениях часто возникает необходимость в проверке гипотез о равенстве математических ожиданий, соответствующих выборкам, извлеченным из двух или более генеральных совокупностей (проверка гипотез об однородности математических ожиданий).

В общем случае гипотеза о равенстве математических ожиданий, соответствующих  выборкам, имеет вид

при конкурирующей гипотезе

,

хотя бы для одной пары индексов.

Для проверки гипотезы  может использоваться ряд критериев. Сюда относятся параметрические критерии, распределения статистик которых получены в предположении о принадлежности наблюдений нормальному закону: критерий сравнения двух выборочных средних при известных и равных дисперсиях; при неизвестных, но равных дисперсиях (двухвыборочный критерий Стьюдента; многовыборочный F-критерий); при неизвестных и неравных дисперсиях (проблема Беренса-Фишера: критерий Крамера-Уэлча); критерий сравнения средних значений двух малых выборок Лорда [1]. Для этих же целей предназначена целая совокупность непараметрических критериев, например, U-критерий Уилкоксона, критерий Манна–Уитни, H-критерий Краскела–Уаллиса [1].

Для упомянутых критериев либо известны распределения статистик при справедливости , либо в литературных источниках приводятся таблицы процентных точек.

Относительно критериев однородности математических ожиданий исследователей волнует три группы вопросов. Во-первых, насколько хорошо описывается распределение статистики теоретической моделью или, начиная с каких объемов выборок можно уверенно пользоваться известными предельными распределениями статистик? Во-вторых, что происходит с распределениями статистик параметрических критериев при нарушении предположений о нормальности наблюдаемых величин? В-третьих, какова мощность критериев по отношению к конкретным альтернативам, и какие критерии в этом смысле наиболее предпочтительны?

Методы и результаты исследований

Исследования распределений статистик критериев проводились методами статистического моделирования. Были исследованы распределения статистик всех упомянутых выше критериев.

В качестве примера рассмотрим поведение статистики критерия сравнения двух выборочных средних при неизвестных, но равных дисперсиях (критерий Стьюдента) в случае нарушения предположения о принадлежности наблюдаемых величин нормальному закону. Статистика критерия имеет вид

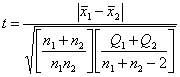 ,                                                 (1)

где  – объем i-й выборки, . В случае нормального закона и справедливости гипотезы  статистика должна подчиняться распределению Стьюдента с числом степеней свободы . Исследования показали, что в случае выполнения предположения о нормальности уже при малых объемах выборок (;) эмпирическая функция распределения статистки достаточно хорошо согласуется с теоретической. Этот вывод касается всех рассмотренных параметрических критериев.

Что происходит с распределениями статистик этих критериев при нарушении предположений о нормальности? В литературе можно встретить массу критических замечаний в адрес исследователей за применение параметрических критериев без проверки нормальности наблюдений, особенно, когда это касается медико-биологических наблюдений, где проверка нормальности или затруднительна вследствие малого числа экспериментов, или заведомо очевидна “ненормальность” данных. В то же время наши исследования показали устойчивость к нарушению предположений о нормальности ряда критериев проверки гипотез о средних [2, 3].

Распределения статистик перечисленных выше параметрических критериев были исследованы при различных законах распределения наблюдаемых случайных величин, в частности, в случае принадлежности семейству симметричных законов с плотностью

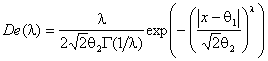
при различных значениях параметра формы .

На рис.1 приведены полученные в результате моделирования эмпирические функции распределения статистики (1) в случае принадлежности наблюдений семейству распределений  с различными параметрами формы.

Картина, представленная на рис.1, типична для всех непараметрических критериев проверки гипотез о средних.

Главный вывод из исследования распределений статистик непараметрических критериев проверки однородности средних заключается в следующем: распределения статистик устойчивы к существенным отклонениям наблюдаемых величин от нормального закона. В частности, для статистики (1) использование в качестве распределения статистики соответствующего распределения Стьюдента не приведет к значительным ошибкам в определении достигнутого уровня значимости, если наблюдаемый закон меняется от распределения Лапласа до почти равномерного. Не очень заметно сказывается асимметричность законов. Существенные изменения в распределениях статистик наблюдаются только в случае принадлежности наблюдений законам с очень “тяжелыми хвостами”.

 В случае применения непараметрического критерия Краскела-Валлиса наблюдения  упорядоченных или неупорядоченных по рангам выборок объёмами  располагают по возрастанию и ранжируют от 1 до n, где n – суммарный объём всех выборок. Пусть  - сумма рангов i-й выборки. Статистика критерия имеет вид:

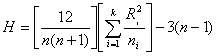.                                       (2)

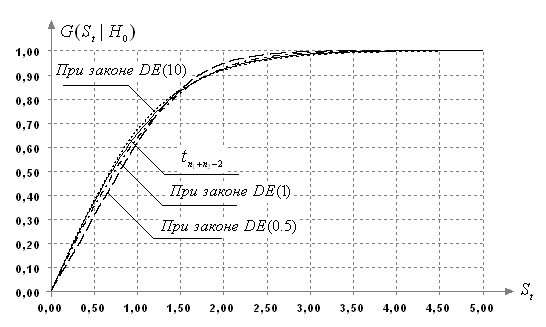
Рис.1 Функция распределения статистики (1) при объемах выборок и различных законах наблюдаемых величин

Предельным распределением статистики  критерия Краскела-Валлиса является –распределение. С помощью методов статистического моделирования распределений статистики было найдено, начиная с каких минимальных объёмов выборок (), достигается хорошая близость эмпирических распределений статистики (2) соответствующим предельным в зависимости от количества выборок k (таблица 1).

Таблица 1. Минимально необходимые объемы выборок в зависимости от числа выборок

k	2	3	4	5	6	7	8	9	10	15
	10	11	12	13	14	15	16	17	18	20

Было показано, что сходимость распределения статистики критерия к предельному закону при верной проверяемой гипотезе не зависит от разницы между дисперсиями в выборках.

Статистика S двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки  упорядочиваются в порядке возрастания. Элементы первой выборки  занимают в общем вариационном ряду места с номерами , т.е. имеют ранги . Тогда .

Распределение нормированной и центрированной статистики Вилкоксона

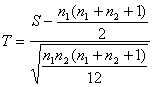,                                                          (3)

где , при росте объёмов выборок приближается к стандартному нормальному распределению.

Были найдены минимальные объёмы обоих выборок, при которых достигается достаточно хорошее согласие дискретного распределения статистики (3) с предельным законом распределения. В общем случае сумма объёмов двух выборок, по которым проверяется гипотеза, должна быть больше, либо равна 50, причем объём каждой выборки не должен быть меньше 5:

Естественно, что на распределения статистик непараметрических критериев проверки однородности средних не влияет закон распределения наблюдаемых величин. В работе было исследовано влияние на распределение статистики (3) неравенства дисперсий, соответствующих анализируемым выборкам. В таблице 2 представлены усреднённые по 50 экспериментам достигаемые уровни значимости при проверке согласия эмпирического и предельного распределения в случае неравенства дисперсий в выборках. Если взять в качестве  минимально допустимого уровня значимости величину 0.3, то можно сказать, что достаточно хорошее согласие достигается, если дисперсия одной из выборок не превышает дисперсию второй более чем в 3 раза.  

Таблица 2. Усреднённый уровень значимости при проверке согласия по критерию Пирсона эмпирического распределения статистики (3) с предельным стандартным нормальным в случае неравенства дисперсий, , объем выборки статистик .

Разница между дисперсиями
Достигнутый уровень значимости	0.5368	0.3836	0.3296	0.2314	0.1316	0.0608	0.0501

Заключение

Распределения статистик непараметрических критериев проверки однородности средних (Стьюдента, Крамера-Уэлча, F-критерия и др.) устойчивы к существенным отклонениям наблюдаемых величин от нормального закона. Существенные изменения в распределениях статистик наблюдаются только в случае принадлежности наблюдений законам с очень “тяжелыми хвостами”. Это позволяет в случае применения данных критериев менее строго относиться к обязательности выполнения предположений о нормальности наблюдаемых величин.

Исследования мощности параметрических и непараметрических критериев на ряде альтернатив показали некоторые преимущества непараметрических критериев.

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а).

Литература

1. Закс Л. Статистическое оценивание. М.: Статистика, 1976. – 598 с.

2. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3.- С.3-15.

3. Lemeshko B.Yu., Lemeshko S.B., Pomadin S.S., Mirkin E.P. Investigation Of The Stability Of Statistical Hypotheses Testing Procedures Used In Quality Management Problems // Proceedings of the Seventh International Conference “Computer Data Analysis and Modeling: Robustness and Computer Intensive Methods”, 2004, Minsk. Vol. 1. – P. 90-93.