См. также: Прикладная математическая статистика (материалы к семинарам)

 

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СТАТИСТИКИ КРИТЕРИЯ ШЕФФЕ ПРИ ЗАКОНАХ ОШИБОК НАБЛЮДЕНИЙ, ОТЛИЧАЮЩИХСЯ ОТ НОРМАЛЬНОГО

 

Б.Ю. Лемешко, В.М. Пономаренко

Новосибирский государственный технический университет

Тел. сл. (383) 346-06-00. E-mail: vikpon@ngs.ru

Аннотация. Методами статистического моделирования исследуются распределения статистики критерия, предложенного Шеффе, при нарушении предположений о нормальном законе распределения ошибок наблюдений. Приводятся сведения об объемах выборок, при которых в качестве приближения предельного распределения статистики можно использовать –распределение. Исследуется влияние вида закона ошибок наблюдений на требуемый объем выборок.

 

Постановка задачи

В данной работе рассматривается приближенный критерий проверки однородности дисперсий, предложенный Шеффе (далее критерий Шеффе), который по предположению автора [1] должен быть очень устойчив к нарушению предположений о нормальности.

Критерии однородности дисперсий в дисперсионном анализе принято рассматривать относительно однофакторной модели вида:

, , .                                  (1)

В этом случае совокупности наблюдений  при различных значениях  могут рассматриваться как элементы выборок из  генеральных совокупностей с математическим ожиданием равным , дисперсией  для -той генеральной совокупности. В классической постановке предполагается, что все наблюдения распределены по нормальному закону.

Проверяемая гипотеза имеет вид

,                                              (2)

а конкурирующая с ней –

,                                                     (3)

где неравенство выполняется, по крайней мере, для одной пары индексов  и .

В критерии Шеффе статистика опирается не на собственно оценки дисперсий, как это обстоит в случае большинства критериев однородности дисперсий, а на средние значения логарифмов оценок дисперсий. При таком подходе задача сводится к сравнению средних, а критерии проверки гипотез “о средних” устойчивы к отклонениям ошибок наблюдений от нормального закона. Применяемое логарифмирование позволяет приблизить распределение статистики критерия к нормальному закону.

Чтобы перейти к сравнению средних, каждая -я выборка наблюдений , , разбивается на  групп объемом , так что .

Для удобства обозначим совокупность значений, полученную путем разбиения совокупности всех наблюдений  на подвыборки, через

, , , .                        (4)

Тогда статистика критерия Шеффе [1] может быть записана в следующем виде:

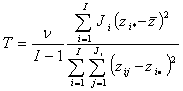
,                                            (5)

где

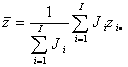, , ,                                         (6)

а значения , выступающие в роли исходных наблюдаемых значений для критерия сравнения средних со статистикой (18), вычисляются как

,                                                                (7)

где – выборочная дисперсия подгруппы

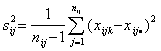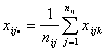, .                                        (8)

По предположению Шеффе статистика  приближенно подчиняется -рас­пределению Фишера  со степенями свободы  и . Причем распределение статистики не должно зависеть [1] от распределения ошибок наблюдений , поскольку критерий разрабатывался как устойчивый к нарушению предположений о нормальности.

 

Выбранный метод решения

Исследование распределения статистики (5) проводилось методами статистического моделирования. При справедливой проверяемой гипотезе  дисперсия ошибок наблюдения ,  (без потери общности) задавалась равной единице, значения средних отклика на уровнях  (также без потери общности) задавались равными нулю. Выборочные значения наблюдений  формировались в соответствии с видом модели (1). Исследования распределений статистик проводились при различных законах ошибок наблюдений и случайного фактора модели (1): нормальном, распределении максимальных значений (Max), семействе распределений

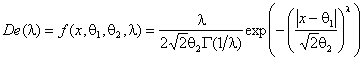
при значениях параметра формы =0.5, 1, 5, 10. Объем моделируемых выборок статистик составлял .

Проверка согласия полученных в результате моделирования эмпирических распределений статистик соответствующим теоретическим функциям распределения осущес­твля­лась по критериям  Пирсона, Колмогорова,  Крамера-Мизеса-Смирнова,  Андерсона-Дарлинга [2, 3]. При проверке согласия использовалась программная система ISW, в рамках которой реализованы результаты, полученные с помощью методики компьютерного моделирования, развиваемой на кафедре Прикладной математики НГТУ [4].

 

Полученные результаты

В таблице 1 приведены достигнутые уровни значимости, полученные при проверке согласия эмпирического распределения статистики (5) и соответствующего теоретического распределения Фишера в случае принадлежности ошибок измерений нормальному закону. В таблице для ряда заданных значений  и  указаны достигнутые уровни значимости для тех минимальных значений , при которых уже наблюдается некоторое согласие сравниваемых распределений. Это согласие трудно назвать хорошим, но, как показывают исследования, при таких значениях  использование соответствующего -распределения в качестве предельного распределения статистики (5) уже не приведет к большим ошибкам при вычислении соответствующих вероятностей. Графики эмпирических распределений, полученные в случае размерностей, представленных в таблице 1, и соответствующих теоретические распределения практически сливаются.

Как показывают исследования, согласие эмпирических и соответ­ству­ющих теоретических распределений статистики (5) растет с ростом . Это дает основания считать уровень согласия, отражаемый в таблице 1 (минимально) допустимым для того, чтобы при таких объемах выборок рекомендовать к использованию в качестве предельного распределения статистики (5) соответствующее -распределение.

 

Таблица 1

Достигнутые уровни значимости, полученные при проверке согласия эмпирических распределений статистики (5) с соответствующими -распределениями при справедливости гипотезы  вида (2) и нормальном законе ошибок наблюдений

Критерий

согласия

Размерность задачи;

-распределение, с которым проверяется согласие

=2,=2, =5;

=2,=5 =4;

=5,=2, =6;

=5, =5, =4;

Отношения правдоподобия

 Пирсона 

Колмогорова 

 Мизеса 

 Андерсона-Дарлинга

0.22

0.22

0.22

0.24

0.24

0.21

0.21

0.11

0.09

0.09

0.14

0.14

0.18

0.16

0.12

0.12

0.12

0.16

0.16

0.14

 

Было исследовано, при каких значениях  ( и ) при заданном значении  и нормальном законе ошибок наблюдений достаточно высока близость эмпирического распределения статистики (5) и соответствующего теоретического распределения Фишера. Рассматривались значения  в диапазоне от 2 до 5,  в диапазоне от 2 до 6.

По результатам исследований сделаны следующие выводы. Мини­мальное значение , при котором допустимо использовать -распределение в качестве предельного распределения статистики (5), составляет 10-12 наблюдений в группе.

Необходимый для приемлемого согласия объем  в существенной степени определяется выбором числа . Например, при =2 минимально допустимый объем  составляет 10-12, при =4 – 16-20, а при =6  –  20-25.

В целом следует отметить, что при нормальном законе ошибок и числе  в группах около 30 наблюдений, можно без риска совершения больших ошибок использовать -распределение в качестве предельного распределения статистики (5) при условии, что будет выбрано разбиение, в котором .

Но, если объем выборок  меньше этого числа, что довольно часто встречается в дисперсионном анализе, то для того, чтобы распределение статистики (5) хорошо согласовалось с соответствующим -распределением, следует выбирать такое разбиение на подгруппы, чтобы  было наибольшим, а  - наименьшим из возможных.

В таблице 2 для случая =5, =5, =4 представлены достигнутые уровни значимости при проверке согласия получаемых в результате модели­рования эмпирических распределений статистики (5) и предполагаемого -распределения Фишера при отличных от нормального законах наблюдений .

Из таблицы следует, что на самом деле распределение  оказывает влияние на степень близости эмпирических распределений статистики (5) с распределениями Фишера. В случае распределения с "тяжелыми" хвостами (например, ) наблюдается очень высокая степень соответствия распределения статистики (5) тому -распределению Фишера, которое должно быть в “нормальном” случае. Из таблицы 2 видно, что в случае принадлежности наблюдений закону распределения  степень близости распреде­ления статистики (5) к -распределению существенно выше, чем в нормальном случае. В случае принадлежности наблюдений асимметричному распределению максимальных значений – степень близости несколько выше, чем в нормальном случае. А вот при ошибках наблюдений по законам с "легкими" хвостами, например,  и  согласия распределения статистики (5) с -распределением при =5, =4 уже практически не наблюдается. В то же время в случае =2, =10 при законах распределений ошибок наблюдений  и  согласие достигает приемлемого уровня.

В целом результаты исследований позволяют рекомендовать при разбиении наблюдений на подгруппы делать это так, чтобы объем подгруппы  был максимален.

 

Таблица 2

Значения достигнутых уровней значимости, полученных в результате проверки согласия эмпи­рического распределения статистики (5) с теоретическим -распределением при справедливости гипотезы  вида (2) при =5, =20 (=5, =4) при различных законах распределения ошибок

Критерий

Согласия

Распределение ошибок наблюдений

Отношения правдоподобия

 Пирсона

Колмогорова

 Мизеса

 Андерсона-Дарлинга

0.2162

0.2176

0.1526

0.1896

0.1751

0.5199

0.5195

0.5431

0.5291

0.5158

0.0034

0.0037

0.0395

0.0323

0.0112

0.0014

0.0014

0.0399

0.0225

0.0078

 

Исследования показали, что наблюдаемые различия в степени близости распре­деления статистики (5) и соответствующего распределения Фишера при различных законах распределения наблюдений  объясняется тем, как распределены , непо­средственно входящие в статистику  (5). Распределение  становится тем сим­мет­ричнее, чем "тяжелее" хвосты распределения наблюдений . Так, в случае принад­лежности  закону  распределение  наиболее симметрично, в случае принад­лежности  закону  распределение  наименее симметрично.

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а).

Литература

1.      Шеффе Г. Дисперсионный анализ. – М.: Физматгиз. – 1963. – 628 с.

2.      Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов, 2002. – 87 с.

3.      Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непа­раметрические критерии. – М.: Изд-во стандартов, 2002. – 64 с.

4.      Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. – Новосибирск: Издательство НГТУ, 1995. – 125 с.