См. также: Прикладная математическая статистика (материалы к семинарам)

Материалы VIII международной конференции “Актуальные проблемы электронного приборостроения” АПЭП-2006. Т.6, Новосибирск, 2006. – С. 91-94.

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЯ ОЦЕНОК КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ В ЗАВИСИМОСТИ ОТ ИСТИННОГО ЗНАЧЕНИЯ КОРРЕЛЯЦИИ

Б.Ю. Лемешко, А.В. Танасейчук

Новосибирский государственный технический университет

Тел. сл. (383) 346-37-52, E-mail: headrd@fpm.ami.nstu.ru, awtan@yandex.ru

Аннотация. Исследованы распределения оценок коэффициента корреляции Пирсона, ранговых коэффициентов корреляции Спирмена, Кендалла в зависимости от истинного значения коэффициента корреляции. Показаны возможности z-преобразования Фишера по приведению к нормальному закону статистик для данных коэффициентов корреляции.

Постановка задачи

В задачах корреляционного анализа для проведения полноценного статистического анализа свойств исследуемого набора данных немаловажную роль играет оценка существующей между некоторыми случайными величинами корреляции. Коэффициент парной корреляции Пирсона между случайными величинами x и y определяется соотношением

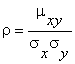где – это ковариация между величинами x и y, а и – среднеквадратичные отклонения величин x и y соответственно. Дав определение парному коэффициенту корреляции как теоретической характеристике двух случайных величин, приведем формулу, по которой вычисляется эмпирический (выборочный) аналог этой характеристики:

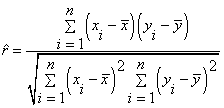где и – выборочные средние для случайных величин x и y.

Для проведения статистического анализа данных, основанного на этой выборочной характеристике, необходимо знать ее статистические свойства. Это позволит судить о точности приближения к истинному значению , строить статистические критерии для проверки различных гипотез о численных значениях анализируемого коэффициента корреляции, конструировать доверительные интервалы для истинного значения коэффициента корреляции. В классической математической статистике известны приближенные выражения для распределения в случае , а также для распределения величины

известной как z-преобразование Фишера для выборочного коэффициента корреляции [1].

Целью данной работы является исследование распределений оценок , , а также распределений оценок ранговых коэффициентов корреляции Спирмена и Кендалла при различных истинных значениях коэффициентов корреляции .

Ранговые коэффициенты корреляции

Ряд объектов, упорядоченных в соответствии со степенью проявления некоторого свойства, называют ранжированным; каждому числу такого ряда присваивается ранг. Ранги обычно обозначают порядковыми числительными 1,2,…,n, где n – количество объектов. Меры взаимосвязи между парой признаков, каждый из которых ранжирует изучаемую совокупность объектов, называются коэффициентами ранговой корреляции.

Коэффициенты ранговой корреляции могут использоваться не только для анализа взаимосвязи ранговых признаков, но и при определении силы связи между ранговыми и количественными признаками, а также и между двумя количественными признаками. В таких случаях значения количественных признаков упорядочиваются и им приписываются соответствующие ранги. Существует ряд ситуаций, когда вычисление коэффициентов ранговой корреляции целесообразно при определении тесноты связи именно двух количественных признаков. Например, если связь двух количественных признаков имеет нелинейный (но монотонный) характер. Если количество объектов в выборке невелико или если для исследователя существенен знак связи, то использование корреляционного отношения может оказаться неадекватным. Вычисление же коэффициента ранговой корреляции позволяет обойти указанные трудности.

Обычно рассматривают коэффициенты ранговой корреляции Спирмена и Кендалла [1, 2]. Оценка коэффициента ранговой корреляции Спирмена имеет вид:

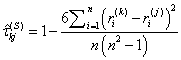где – ранг i-го объекта в j-м наборе данных.

Оценка коэффициента ранговой корреляции Кендалла вычисляется как:

где – количество инверсий в наборе данных по отношению к , вычисляется как

где

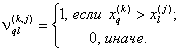
Распределения выборочных коэффициентов корреляции

Из классической теории известно, что выборочный коэффициент в предположении нормального распределения величин x и y и при достаточно больших объемах выборок подчиняется нормальному закону с математическим ожиданием и дисперсией 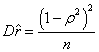. Относительно ранговых коэффициентов Спирмена и Кендалла также говорится, что их распределение близко к нормальному.

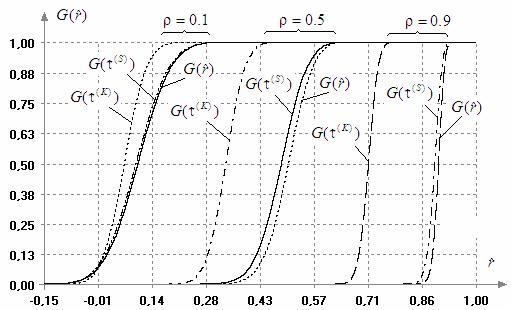
На следующем рисунке приведены распределения коэффициентов , , при различных истинных значениях :

В таблице 1 приведены результаты моделирования распределений коэффициентов , , и проверки согласия полученного эмпирического распределения с нормальным законом. Курсивом приведены достигнутые уровни значимости при проверке согласия с нормальным законом, с указанными выше параметрами. Остальные значения – результат проверки сложной гипотезы о согласии с нормальным распределением, параметры которого оценивались по выборке. Для проверки гипотез использовался критерий отношения правдоподобия.

Таблица 1. Достигнутые уровни значимости при проверке согласия с нормальным законом распределений оценок коэффициентов корреляции, объем выборок n=200.

Коэффициент корреляции	Достигаемый уровень значимости
Коэффициент корреляции	Истинное значение	Истинное значение	Истинное значение
	0. 70832 0. 92835	5.8793e-08 2.4997e-07	4.1965e-28 5.0311e-28
	0. 27019	0. 00020153	1.4358e-43
	0.20108	0.23364	4.3142e-08

Как видим, с ростом истинного значения распределения оценок рассмотренных коэффициентов все существеннее отличаются от нормального закона. Наиболее близким к нормальному распределению при близких к единице значениях оказалось распределение оценок коэффициента (Кендалла).

Z-преобразование Фишера

При проверке гипотез и построении доверительных интервалов для коэффициентов корреляции часто пользуются z-преобразованием Фишера . Это преобразование дает величину, распределение которой значительно ближе к нормальному с приближенными математическим ожиданием и дисперсией . В таблице 2 приведены результаты применения преобразования Фишера как к коэффициенту , так и к коэффициентам и . В последнем случае не рассчитывали получить хорошее согласие с нормальным законом 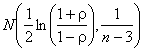, но все же ожидали получить распределение, более близкое к нормальному, чем распределения самих коэффициентов и .

Таблица 2. Достигнутые уровни значимости при проверке согласия с нормальным законом выборок Z-преобразования Фишера, объем выборок n=200.

Коэффициент корреляции

Достигнутый уровень значимости

Истинное значение

0.84335

0.77419

0.38891

0.76534

0.38304

0.16866

0.088276

5.8136e-07

0.13055

0.48714

0.086366

0.5826

0.19934

Как видим, применение z-преобразования в случае значений близких к 1 позволяет перейти к нормальной аппроксимации для оценок рассматриваемых коэффициентов, а в случае с коэффициентом – к распределению .

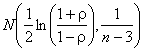Результаты

Таким образом, показано, что с ростом истинного значения коэффициента корреляции распределения выборочных коэффициентов , и начинают существенно отклоняться от нормального. Наиболее устойчивым к высоким значениям коэффициентов корреляции (наиболее близким к нормальному закону при больших значениях ) показало себя распределение оценок коэффициента ранговой корреляции Кендалла .

Использование z-преобразования Фишера для оценок коэффициентов корреляции позволяет с большим основанием использовать аппроксимацию нормальным законом. В том числе для коэффициентов ранговой корреляции, однако, с некоторыми другими параметрами нормального закона. Особенное значение это имеет именно при близких к единице значениях , так как открывает возможность построения доверительных интервалов для рассмотренных коэффициентов корреляции при значениях .

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а).

Литература

1. Кендалл М.Дж., Стьюарт А. Статистические выводы и связи. - М.: Наука, - 1973. - 899 с.

2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: Юнити, – 1998. – 1022 с.