УДК 519.2

 

Б.Ю. Лемешко, С.Н. Постовалов, А.В. Французов

(Новосибирск)

К ПРИМЕНЕНИЮ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СОГЛАСИЯ ДЛЯ ПРОВЕРКИ АДЕКВАТНОСТИ НЕПАРАМЕТРИЧЕСКИХ МОДЕЛЕЙ[1]

 

Показана возможность применения непараметрических критериев согласия типа Колмогорова, типа  и  Мизеса для проверки адекватности непара­метриче­ских моделей законов распределения. Показано, что при использовании непара­метрических оценок на распределения статистик критериев согласия влияет ряд факторов, определяющих сложную проверяемую гипотезу : закон распре­де­ления наблюдаемой случайной величины, соот­вет­ствующий ; вид использу­емой ядерной функции; объем выборки; метод оценивания параметров размыто­сти.

 

Введение. Построение вероятност­ной модели для некоторого объекта, как правило, включает два этапа. На первом этапе выбира­ется тип модели, при необходимости оцениваются параметры этой модели, на втором – проверя­ется адекватность модели наблюдаемым данным. В параметрической статистике этим этапам соот­ветствует два основных типа задач: оценивания параметров и про­верки статистических гипотез.

В простейшей ситуации, когда мы имеем дело с наблюдаемой случайной величиной, в случае параметрического подхода на первом этапе высказываются предположения о виде модели закона распределения и по выборкам, извлекаемым из генеральной совокуп­ности, оцени­ва­ются параметры этой модели. На втором этапе адекватность модели наблюдаемым данным проверя­ется с использова­нием критериев согласия типа  Пирсона, типа Колмогорова, типа  Мизеса и других.

Естественно, что ограниченное множество параметрических моделей, наиболее часто используемых на практике, не всегда позволяет адекватно описать реально сущест­вующие случайные величины. Последние десятилетия характеризовались интенсивным развитием непарамет­рической статистики, расширением применения непараметрических методов в различ­ных приложениях. Иногда непараметрические методы противопостав­лялись параметрическим. Противопоставление обычно сопровождалось далеко не всегда спра­ведливой критикой параметричес­кого подхода. В процессе такой критики как-то упускается из виду, что применение непараметрических оце­нок наблюдаемых законов распределений также имеет свои узкие места. Например, суще­ствует проблема наилуч­шего выбора параметра (параметров) размытости используемых ядерных оценок функции плотности, которая обостряется в случае ограниченности об­ласти определения наблю­даемой случайной величины и конечности объемов выборок. В последнем случае ядерная оценка функции распределения зачастую существенно отлича­ется от эмпирической функции распределения на границах области (на “хвостах” распре­деления). Но наиболее важно то, что пока остаются открытыми вопросы проверки адекватности непараметричес­ких моделей.

На наш взгляд, излишне негативное отношение некоторых авторов к параметриче­ским методам и противопоставление им непараметрических ничем не оправдано: приме­нять следует те методы, которые в конкретной ситуации дают наилучший результат. Параметрические и непараметрические методы не являются взаимоисключающими, а с развитием математического аппарата граница между ними начинает размываться. Например, как только мы начинаем говорить об оптимальном выборе параметра размытости в непара­мет­ричес­кой модели, стирается принципиальное отличие такой модели от параметрической. С другой стороны, непараметрические модели и методы имеют ряд конкретных достоинств, обуславливающих возрастающий интерес к ним в различных приложениях.

В настоящий момент практически все силы статистиков направлены на нахождение более точных непараметрических оценок, на исследование свойств этих оценок. Проблема же проверки того, насколько полученная непараметрическая модель закона адекватна истинному, обходится вниманием исследователей. Проверка адекватности модели представляет собой заключительный этап статистического анализа, следующий за построением параметрической или непараметрической модели наблюдаемого закона, обос­новывающий возможность применения данной модели в конкретном приложении. Отсутствие аппарата проверки адекватности непараметрических моделей препятствует широкому применению методов непараметрической статистики на практике.

Целью данной работы явилось исследование возможности проверки адекватности непараметрических моделей с применением непарамет­рических критериев согласия типа Колмогорова, типа  и  Мизеса.

Простые непараметрические оценки плотности. В качестве непараметрических моделей в работе рассматриваются непараметрические оценки плотности Розенблата–Парзена, которые имеют вид 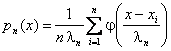[1]

,                                                    (1)

где  – выборка наблюдений одномерной непрерывной случайной величины,  – параметр размытости, а  – колоколообразная (ядерная) функция, удовлетво­ряющая следующим условиям регулярности:

;  ;  ;    ;

;  .                                                  (2)

Асимптотические свойства оценки (1), такие как немещенность, состоятельность, сходимость почти наверное к плотности , подробно исследованы в работах [2-4]. В частности, показано, что среднеквадратическая ошибка аппроксимации оценки (1), опре­деляемая соотношением

,                             (3)

существенно зависит от выбора параметра размытости  и в меньшей степени от вида ядерной функции .

В исследованиях данной работы используются ядерные функции двух видов:

1)        квадратичная ядерная функция [4], обладающая наилучшими свойствами при мини­мизации среднеквадратичной ошибки аппроксимации (3)

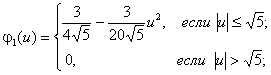                                             (4)

2)        функция плотности стандартного нормального закона

.                                                          (5)

Выбор параметра размытости  оказывает существенное влияние на вид непара­метрических оценок функции плотности. И всегда существует проблема нахождения зна­чения этого параметра, оптимального в определенном смысле. Если исходить из условий минимума среднеквадратической ошибки аппроксимации (3), то оптимальная оценка па­раметра размытости принимает вид [4]:

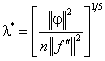.                                                          (6)

Недостатком оценки (6) является то, что для ее определения необходимо знать плот­ность  истинного закона распределения случайной величины, который, вообще го­воря, не известен.

При  выражение (6) стремится к . Вследствие этого иногда предлагают параметр размытости выбирать равным

.                                                              (7)

Вообще говоря, выбор параметра (или параметров) размытости может осуществ­ляться различными методами, на основании различных критериев оптимальности [5], на­пример, с использованием различных мер близости эмпирической функции распределения и ее непраметрической оценки. Однако в этом случае теряются преимущества непарамет­рических оценок относительно параметрических моделей.

Исследование поведения распределений статистик непараметрических крите­риев согласия при непараметрическом оценивании. Проверка адекватности парамет­рической модели закона распределения наблюдаемым данным чаще всего осуществляется с использованием критериев согласия типа  Пирсона или непараметрических критериев типа Колмогорова, типа  и  Мизеса.

При использовании критериев согласия следует различать простые и сложные гипо­тезы. Простая про­веряемая ги­потеза имеет вид : , где  – функция рас­пределения веро­ятностей, с которой проверяется со­гла­сие наблюдаемой вы­борки, а  – из­вестное значение параметра (скалярного или векторного). Сложная проверяемая гипо­теза записывается в виде : . Со сложной гипотезой, например, имеем дело в том случае, если ее проверка осуществляется по той же выборке, по которой оценивались и параметры закона распределения.

В критерии Колмого­рова в качестве расстояния между эмпирическим и теоретиче­ским законом ис­пользуется величина

,

где  – эмпирическая функция распределения,  – теоретическая функция рас­пределения,  – объём выборки. Обычно ис­пользуется стати­стика вида [6]

,                                                              (8)

где

, , ,

 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция закона распределения, согласие с которым про­ве­ряется. Распределение величины  при простой гипотезе в пределе подчиня­ется закону Колмо­горова  [6].

В критериях типа  расстояние между гипотетическим и истинным распределе­ниями рассматривается в квадратичной метрике

,

где   - оператор математического ожидания.

При выборе  в критериях типа  Мизеса пользуются статис­ти­кой (стати­стика Крамера-Мизеса-Смирнова) вида

,                                     (9)

которая при простой гипотезе подчиняется распределению  [6].

При выборе  в критериях типа  Мизеса статистика (статистика Ан­дерсона-Дарлинга) имеет вид

.               (10)

В пределе эта статистика подчиняется распределению  [6].

В случае простых гипотез предельные распределения статистик непара­мет­рических критериев типа Колмогорова,  и  Мизеса не зависят от вида наблюдаемого закона распределения и от его параметров. Именно поэтому эти критерии называют непарамет­рическими и говорят, что они являются “свободными от рас­пределения”. Но при проверке сложных гипотез свойство “свободы от рас­пределения” теряется [7]. Как выяснилось, на условные за­коны рас­пределения статистик  непараметрических критериев согла­сия влияет целый ряд факторов, опреде­ляющих “сложность” гипотезы: вид наблюдаемого за­кона , соот­вет­ству­ющего истин­ной гипотезе ; тип оцениваемого пара­метра и коли­чество оцениваемых параметров; в некоторых ситуациях конкретное значение пара­метра (например, в случае гамма-рас­пре­деления); используемый метод оценивания пара­метров [8-11].

В настоящей статье излагаются результаты продолжения исследований, начатых в  [12]. Основной целью данной работы явилось исследование возможности применения не­параметрических критериев согласия для проверки адекватности непараметрических мо­делей законов распределений (непараметрических оценок). Для этого, опираясь на мето­дику компьютерного моделирования статистических закономерностей [8-11], исследова­лось: как зависят распределения статистик вышеупомянутых критериев согласия от типа ядерных функций; как меняется вид этих распределений с ростом объема выборки; как за­висят распределения статистик от закона, соответствующего проверяемой гипотезе ; как отражается на распределениях статистик оценивание параметра размытости.

При непараметрическом подходе мы также как и при параметрическом сталкиваемся с проверкой простых и сложных гипотез. Допустим, по некоторой ранее наблюдаемой выборке  мы получили непараметрическую оценку плотности вида (1). Значения , , …,  можно трактовать как параметры этой модели

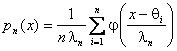.                                                   (11)

Если проверка адекватности непараметрической оценки осуществляется по новой вы­борке, объем которой необязательно тот же самый, то, очевидно, что мы будем иметь дело с простой проверяемой гипотезой. Это классический случай, при котором статистики кри­териев типа Колмогорова,  и  Мизеса при справедливости проверяемой гипотезы  должны подчиняться, соответственно, распределениям , , .

Для того чтобы удостовериться в том, что в случае простой гипотезы предельными распределениями статистик  действительно являются распределения , ,  выборки случайных величин, соответствующие гипотезе , моделирова­лись в соответствии с моделью (11) по методу обратных функций. Моделирование под­твердило, что получаемые эмпирические распределения статистик исследуемых крите­риев хорошо согласуются с классическими предельными законами, соответственно, ,  и . Например, на рис. 1 представлены результаты моделирования распределе­ния статистики типа Колмогорова при объеме выборок моделируемых случайных величин  = 50 и количестве таких выборок  N = 500. На рисунке приведены результаты проверки согласия полученного эмпирического распределения с распределением  по крите­риям  Пирсона, отношения правдоподобия, Колмого­рова, Смирнова,  и  Мизеса с отражением по каждому критерию достигнутого уровня значимости 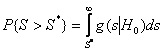, где  - значение статистики критерия, вычисленное по выборке,  - плотность предельного распределения статистики соответствующего критерия при справедливости гипотезы . 

В параметрическом случае мы сталкиваемся со сложной гипотезой, если проверке предшествует оценивание параметров модели по этой же самой выборке. Для непарамет­рической модели такой ситуации, в привычном понимании, соответствует случай оцени­вания по конкретной выборке параметра (или параметров) размытости. С другой стороны, при построении по выборке модели (1) происходит неявная оценка ее параметров , , …,  [см. модель в форме (11)]. И проверяя согласие с этой моделью по этой же выборке, даже без оценки параметра размытости мы, вообще говоря, также имеем дело со сложной гипотезой. Чтобы выделить эту наиболее часто встречаемую на практике ситуацию и подчеркнуть, что в данном случае не происходит оценивания параметров ка­ким-либо методом, назовем ее проверкой “квазисложной” гипотезы.

 

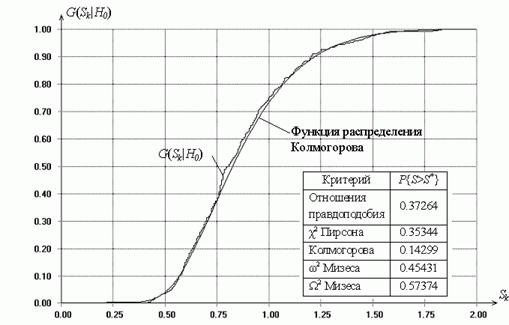
Рис. 1. Распределение статистики Колмогорова при простой гипотезе

 

Как и в параметрическом случае, при проверке сложных (квазисложных) гипотез распределения статистик критериев типа Колмогорова, типа  и  Мизеса зависят от истинного закона распределения, соответствующего гипотезе  [7-10]. Рисунки 2–4, на которых представлены результаты моделирования распределений статистик критериев типа Колмогорова, типа  и  Мизеса при проверке “квазисложных” гипотез , де­мон­стрируют, как зависят распределения статистик от вида истинного закона распределе­ния, соответствующего . При моделировании параметры , , …,  модели (11), соответствующей истинной гипотезе , выбирались таким образом, чтобы она была близкой к одной из следующих параметрических моделей: экспоненциальному закону с плотностью , закону распределения Коши с плотно­стью  или логистическому распределению с плотностью 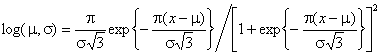. Выборки случайных величин объемом  = 50 моделировались по модели (11). Для формирования выборки статистик эксперимент повторялся N = 500. Полученные результаты наглядно подтверждают, что при проверке квазисложных гипотез распределения статистик существенно зависят от ис­тинного закона, соответствующего , и сильно отличаются, соответственно, от распре­делений Колмогорова,  и , которые являются предельными в случае простых гипотез.

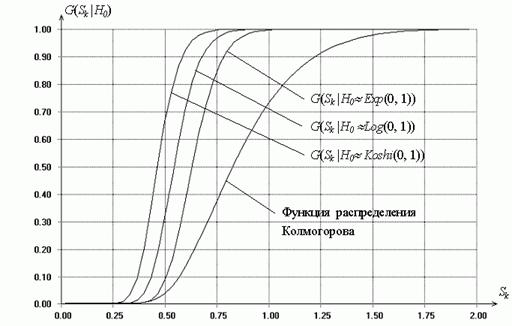
Рис. 2. Распределения статистики типа Колмогорова при “квазисложной” гипотезе в зависимости от истинного закона, соответствующего гипотезе

 

В параметрическом случае распределения статистик  непараметрических критериев согласия типа Колмогорова, типа  и  Мизеса зависят от объема выборок , но с ростом  очень быстро сходятся к предельным, как при простых, так и сложных гипотезах. Практически, начиная с объемов выборок  при проверке простых гипотез и  при проверке сложных, можно пользоваться предельными распреде­лениями статистик [8].

В случае непараметрических моделей при проверке сложных (квазисложных) гипо­тез прослеживается несколько большая зависимость от  и более медленная сходимость распределений статистик к предельным. Рис. 5 показывает характер изменения распреде­лений статистики критерия типа  Мизеса при “квазисложной” гипотезе в зависимости от объема выборки случайных величин. В данном случае при моделировании параметры , , …,  модели (11), соответствующей истинной гипотезе , выби­рались таким образом, чтобы она была близкой к логистическому закону. Аналогичным образом меняются с ростом  и распределения статистик критериев типа Колмогорова и типа  Мизеса.

 

 

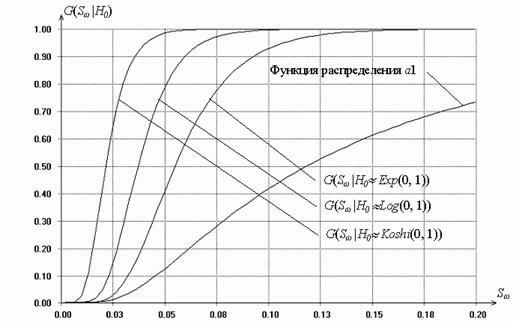
Рис. 3. Распределения статистики типа  Мизеса при “квазисложной” гипотезе в зависимости от истинного закона, соответствующего гипотезе

 

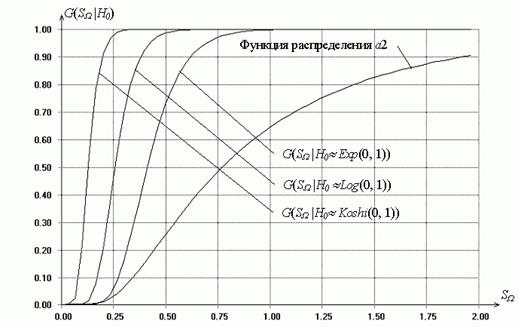
Рис. 4. Распределения статистики типа  Мизеса при “квазисложной” гипотезе в зависимости от истинного закона, соответствующего гипотезе

 

Тип используемых ядерных функций также оказывает влияние на распределения статистик критериев согласия. Например, рис. 6 иллюстрирует зависимость распределе­ний статистики критерия типа Колмогорова при той же “квазисложной” гипотезе (близкой к логистическому закону) и  от вида используемых ядерных функций (4) и (5). Вид используемых ядерных функций оказывает аналогичное влияние на характер изменения распределений статистик типа  и  Мизеса. Исследования показали, что с ростом объема выборки различие распределений статистик рассматриваемых критериев согласия при использовании разных видов ядерных функций становится более существенным.

 

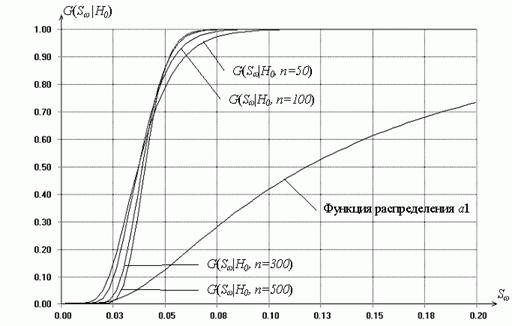
Рис. 5. Изменение распределений статистики  Мизеса при проверке “квазисложной” гипотезы в зависимости от объема выборки

 

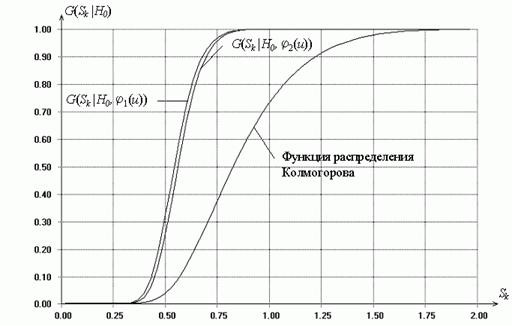
Рис. 6. Влияние типа ядерной функции на распределения статистики типа Колмогорова при проверке “квазисложной” гипотезы

 

При проверке сложных гипотез, когда по наблюдаемой выборке мы оцениваем па­раметр размытости, распределения статистик исследуемых критериев согласия зависят от тех же факторов, что и при “квазисложной” гипотезе, и плюс от метода оценивания пара­метра размытости. Например, рис. 7 показывает распределения статистики критерия со­гласия типа Колмогорова при сложной гипотезе (близкой к логистическому закону),  и различных оценках параметра размытости, вычисляемых в соответствии с соот­ношениями (6) и (7).  На этом же рисунке для сравнения представлены распредления ста­тистики Колмогорова при проверке сложной гипотезы о согласии с логистическим зако­ном (с параметрической моделью) при одновременном вычислении оценок максимального правдоподобия (ОМП) двух параметров этого закона и при использовании MD–оценок, получаемых при минимизации статистики соответствующего критерия согласия [9-11]. Аналогичным образом выбор оценки параметра размытости влияет на изменение распре­делений статистик критериев типа  и  Мизеса.

 

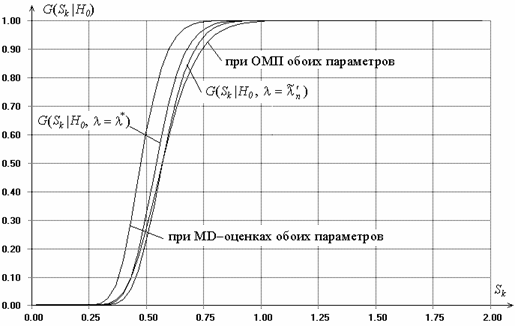
Рис. 7. Влияние метода оценивания параметра размытости на распределение статистики

типа Колмогорова при проверке сложной гипотезы

 

Заключение. Реально с простой проверяемой гипотезой при проверке адекватности непара­мет­рической модели мы имеем дело только в том случае, если построение оценки и проверка согласия проводятся по разным выборкам или по разным частям выборки. Ре­зультаты статистического моделирования подтвердили, что в таких ситуациях процедуры проверки должны опираться на классические результаты о предельных распределениях статистик критериев Колмогорова,  и  Мизеса: распределения Колмогорова,  и , соответственно.

Проверка сложных гипотез о согласии по критериям типа Колмогорова,  и  Мизеса при использовании непараметрических оценок по сравнению с применением па­раметрических моделей отличается большим многообразием факторов, определяющих “сложность” гипотезы. На распределения статистик рассматриваемых критериев сущес­т­венно влияют: истинный закон распределения наблюдаемой случайной величины, соот­вет­ствующий проверяемой гипотезе ; вид используемой ядерной функции; объем вы­борки; метод оценивания (вид оценки) параметра или параметров размытости. По сравне­нию с проверкой согласия с параметрическими моделями особенно следует подчеркнуть большую зависимость распределений статистик от объема выборки. Это объясняется тем, что каждый новый элемент выборки, используемый в непараметрической оценке, является дополни­тельным “оцененным” параметром модели. И в этом состоит принципиальное от­личие от задачи проверки сложных гипотез о согласии с применением параметрических моделей.

Проведенные исследования показали возможность использования непараметриче­ских критериев согласия для проверки адекватности непараметрических моделей законов распределений при проверке простых и сложных гипотез, возможность построения моде­лей распределений статистик критериев согласия для различных проверяемых сложных гипотез.

Очевидно, что многообразие сложных гипотез настолько велико, что построение мо­делей распределений статистик рассматриваемых критериев согласия для каждого опре­деленного вида сложной гипотезы, задаваемой видом непараметрической оценки, заранее невозможно. Однако, опираясь на используемую методику компьютерного моделирова­ния, для конкретной сложной проверяемой гипотезы (закона, соответствующего ; кон­кретного вида непараметрической оценки; объема выборки; метода оценивания параметра размытости) всегда можно построить модель распределения статистики применяемого критерия согласия, а, следовательно, обеспечить проверку адекватности непараметриче­ской модели.

СПИСОК ЛИТЕРАТУРЫ

1.      Parzen E. On the estimation of probability density function and the mode // Ann. Math. Stat., 1962. – Vol. 33. – P.1065-1076.

2.      Надарая Э.А. Об оценке плотности распределения случайных величин // Сообщ. АН ГССР. – 1964. – Т.34. – № 2. – С. 277-280.

3.      Надарая Э.А. Непараметрическое оценивание плотности вероятности и кривой рег­рессии. – Тбилиси: Изд-во ТГУ, 1983. – 194 с.

4.      Епанечников В.А. Непараметрическая оценка многомерной плотности вероятности. Теория вероятностей и ее применения, 1969. – Т.14. – № 1. – с. 156-161.

5.      Лапко А.В., Ченцов С.В. Непараметрические системы обработки информации. . – М.: Наука, 2000. – 350 с.

6.      Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

7.      Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat. – 1955. – V.26. – P.189-211.

8.      Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. 1998. – Т.64. – № 3. – С. 61-72

9.      Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согла­сия опытного распределения с теоретическим. Методические рекомендации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ, 1999. – 85 c.

10.  Лемешко Б.Ю., Постовалов С.Н. Применение непараметрических критериев согла­сия при проверке сложных гипотез // Автометрия. 2001. – № 2. – С. 88-102.

11.  Лемешко Б.Ю., Постовалов С.Н. О зависимости распределений статистик непара­метри­ческих критериев и их мощности от метода оценивания параметров // Заводская лаборатория. Диагностика материалов. 2001. – Т. 67. – № 7. – С. 62-71.

12.  Лемешко Б.Ю., Постовалов С.Н., Французов А.В. Исследование распределений ста­тистики типа Колмогорова при использовании ядерных оценок // Материалы междуна­родной НТК "Информатика и проблемы телекоммуникаций". – Новосибирск, 2001. – С. 82.

 

Новосибирский государственный

технический университет

E-mail: headrd@fpm.ami.nstu.ru


[1] Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 00-01-00913)

 

[Содержание]