См. также: Прикладная математическая статистика (материалы к семинарам)
Измерительная техника. 2006. № 10. – С.9-14
УДК 519.24
КРИТЕРИЙ НЕЗАВИСИМОСТИ АББЕ ПРИ
НАРУШЕНИИ ПРЕДПОЛОЖЕНИЙ НОРМАЛЬНОСТИ
Лемешко С.Б.
Исследованы распределения статистики критерия Аббе при различных вероятностных законах. Показана устойчивость распределений статистики к нарушению предположений нормальности. Оценена мощность критерия относительно различных альтернатив.
Ключевые слова: критерий Аббе, критерий независимости, мощность критерия.
TEST OF INDEPENDENCE ABBE AT INFRINGEMENT OF THE
ASSUMPTION OF THE NORMAL LAW
Lemeshko
S.B.
Distributions
of statistics of Abbe test are investigated at various laws of
distribution of probabilities. Stability of distributions of statistics to infringement
of assumptions of the normal law is shown. Power test various alternatives is
calculated.
Key words: Abbe
test, test of independence, power test.
Введение. Критерий Аббе
предназначен для проверки гипотез вида 
: 
, то есть для проверки того, что все
наблюдаемые величины 
, 
, …, 
в выборке объема 
имеют одинаковые математические
ожидания. Конкурирующая гипотеза (альтернатива) заключается в справедливости 
для всех или некоторых значений
. Критерий часто используют для проверки независимости
последовательности измерений, для проверки отсутствия тренда (отсутствия
систематических изменений).
Статистика критерия Аббе в современной форме [1] представляет собой отношение
,
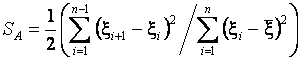(1)
где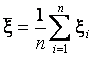 
.
Предполагается, что 
– взаимно независимые,
нормально распределенные случайные величины с одинаковыми, но неизвестными
дисперсиями. Если верна некоторая альтернатива, то знаменатель статистики 
больше числителя и поэтому
значения статистики будут, как правило, меньше тех, которые наблюдаются, когда
справедлива основная гипотеза о равенстве средних.
Условное распределение 
статистики (1) при
справедливости зависит от объема выборки , симметрично относительно 1 и
определено на интервале 
[2]. С ростом объемов выборок распределение
статистики хорошо приближается нормальным законом с параметром сдвига 1 и со
стандартным отклонением при объемах 
, равным [1]
,
(2)
а при 
– с [3]
.
(3)
Решение об отклонении проверяемой гипотезы о равенстве средних
принимается, если значение статистики 
оказывается меньше критического
значения 
, где 
– заданный уровень значимости,
а критическое значение определяется из уравнения 
в соответствии с условным
распределением статистики .
Одной из основных предпосылок применения критерия Аббе является предположение о принадлежности нормальному закону. В работе
[4] в ходе исследования числовых характеристик распределения статистики (1) при
справедливости и принадлежности отсчетов различным симметричным
законам была отмечена устойчивость этих характеристик и самого распределения
статистики Аббе к нарушению предположения о
нормальности .
Для многих статистических критериев нарушение предположения о нормальности приводит к существенным изменениям в законе распределения статистики критерия. Однако, относительно ряда параметрических критериев, связанных с проверкой гипотез о средних, можно говорить о их устойчивости к нарушению такого предположения (при отклонении от нормального закона в достаточно широких пределах). В литературных источниках можно найти аналитические оценки, характеризующие изменения распределений некоторых статистик в связи с определенными отклонениями ошибок измерений от нормального закона. Результаты численных исследований, подтверждающие этот вывод, содержатся, например в [5]. Можно говорить о высокой устойчивости критериев проверки однородности средних двух выборок (например, критериев Стьюдента при известных и неизвестных дисперсиях) или серии выборок (например, F-критерий): как правило, распределения статистик значимо отличаются от “классических” при асимметричности законов наблюдаемых случайных величин или при наличии “тяжелых” хвостов (при законах близких к распределению Коши). Аналогичная ситуация имеет место и в случае критерия Аббе.
Цель данной работы заключалась в исследовании влияния на распределение статистики критерия различной степени отклонения от нормального закона и оценка мощности критерия по отношению к некоторым альтернативам. В частности, исследовалось, что происходит с распределением статистики, если закон распределения наблюдаемых величин асимметричен, с “тяжелыми” хвостами, представляет собой симметричный закон, в различной степени отличающийся от нормального, представляет собой симметричную многомодальную смесь. Исследовалась зависимость распределения статистики от объема выборки. В основу исследований положена методика статистического моделирования распределений статистик.
Степень близости распределений
статистики Аббе к нормальному.
Насколько оправдана
возможность применения в качестве распределения статистики (1) аппроксимации
его нормальным с параметром масштаба (2) или (3) и можно ли использовать такую
аппроксимацию при 
?
В таблице 1 представлены
результаты проверки согласия смоделированных эмпирических распределений
статистик критерия Аббе при нормальности наблюдаемых
величин и справедливости гипотезы при объемах выборок данных 
с нормальными законами распределения,
определяемыми параметрами масштаба (2) и (3). Объемы выборок моделируемых
значений статистик во всех случаях составляли величину 
=10000. Использовался критерий
согласия 
Пирсона при асимптотически оптимальном
группировании [6] и непараметрические критерии Колмогорова, 
Мизеса
(Крамера-Мизеса-Смирнова) и 
Мизеса
(Андерсона-Дарлинга) [7].
Таблица 1. Достигнутые уровни значимости при проверке согласия распределения статистики с нормальным законом с параметром масштаба (2) и (3)
|
Критерий согласия |
|
|
|
|
||||
|
(2) |
(3) |
(2) |
(3) |
(2) |
(3) |
(2) |
(3) |
|
|
|
0,0000 |
0,0000 |
0,0543 |
0,0656 |
0,5849 |
0,2988 |
0,2219 |
0,1725 |
|
Колмогорова |
0,0009 |
0,0000 |
0,1480 |
0,0171 |
0,6073 |
0,4203 |
0,2857 |
0,2701 |
|
|
0,0022 |
0,0000 |
0,2379 |
0,0277 |
0,6134 |
0,4520 |
0,2076 |
0,1800 |
|
|
0,0003 |
0,0000 |
0,1517 |
0,0116 |
0,5189 |
0,2935 |
0,1948 |
0,1549 |
Как следует из приводимых
в таблице достигнутых уровней значимости, при всех значениях объемов выборок формула (3) дает худшую по сравнению
с (2) аппроксимацию для распределения статистики Аббе.
Отсюда, применение формулы (3) при не является
оправданным: предпочтительней использование нормальной аппроксимации с
масштабным параметром (2).
При , не смотря на информацию о
симметричности [2], распределение статистики критерия становится асимметричным.
Например, при 
распределение статистики Аббе заметно асимметрично и существенно отличается от
аппроксимирующего нормального с параметром масштаба, задаваемым соотношением
(2).
Несколько замечаний по
точности моделирования. Построение эмпирических функций распределения
исследуемых статистик с высокой гарантированной точностью требует
значительных объемов моделируемых выборок. В таблице 2 показана зависимость
погрешности 
оценивания функции распределения 
моделируемой статистики 
от числа экспериментов метода
статистических испытаний . В данном случае величина определяет половину длины 90%
доверительного интервала. Точность оценивания значений и 
одинакова. Например, для полученного
значения эмпирической функции распределения статистики 
границы доверительного
интервала, накрывающего истинное значение, составят 
при 
. Повышение
точности на порядок требует увеличения объемов моделирования на два порядка.
Таблица 2. Значения погрешности моделирования функции
распределения статистики в зависимости от числа статистических испытаний
|
|
|
||||||
|
0,5 |
0,4 |
0,3 |
0,2 |
0,1 |
0,05 |
0,01 |
|
|
1000 |
0,0260 |
0,0255 |
0,0238 |
0,0208 |
0,0156 |
0,0113 |
0,0052 |
|
10000 |
0,0082 |
0,0081 |
0,0075 |
0,0066 |
0,0049 |
0,0036 |
0,0016 |
|
100000 |
0,0026 |
0,00255 |
0,00238 |
0,00208 |
0,00156 |
0,00113 |
0,00052 |
|
1000000 |
0,00082 |
0,00081 |
0,00075 |
0,00066 |
0,00049 |
0,00036 |
0,00016 |
В то же время, как
показывает опыт, при построении приближенных параметрических моделей законов
распределения для исследуемых закономерностей увеличение от 104 до 106
практического значения не имеет.
О степени зависимости распределений
статистики Аббе от наблюдаемого закона. В процессе исследований
распределений статистик при справедливой проверяемой гипотезе рассматривалась принадлежность
наблюдаемой выборки нормальному закону распределения с плотностью
,
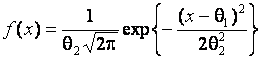а также множеству различных симметричных и несимметричных распределений. В частности, исследовались распределения статистики Аббе и мощность критерия в случае принадлежности отсчетов семейству с плотностью
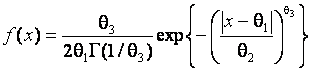(4)
и параметрами формы 
. В частности, при
выражение (4) дает плотность нормального закона
распределения. На рис. 1 представлены полученные в результате моделирования
распределения статистики (1) в случае принадлежности отсчетов законам
распределения семейства (4) при различных параметрах формы: вид закона менялся
от близкого к распределению Коши, до близкого к
равномерному распределению.
Как следует из
представленной на рис. 1 картины, в случае принадлежности достаточно широкому кругу
законов распределение статистики критерия Аббе
существенно не отличается от распределения, имеющего место в случае
принадлежности наблюдений нормальному закону. Если закон, которому принадлежат
наблюдаемые величины, симметричен и с не слишком тяжелыми хвостами, то и когда
он более “плосковершинен” чем нормальный закон, и
когда он более “островершинен” (с большим эксцессом),
распределение статистики не отличается значимо от “классического”.
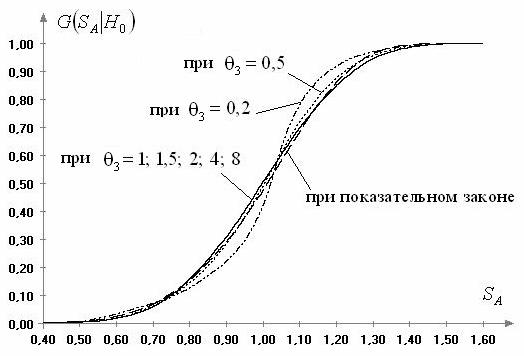
Рис.1.
Распределения статистики критерия Аббе в зависимости
от параметра формы распределения семейства (4) при 
Например, проверка
однородности распределений статистики (1) в случае нормального закона и закона
с параметром 
по критериям Смирнова и Лемана-Розенблатта
[1, 8] показала, что нет оснований для отклонения гипотезы об их однородности.
Проверка однородности осуществлялась по выборкам значений статистик
объемом =10000. Достигнутые уровни значимости составили 0.823
для критерия Смирнова и 0.896 для критерия Лемана-Розенблатта.
С учетом высокой мощности данных критериев при таких
объемах выборок достигнутые уровни значимости говорят о практическом совпадении
распределений, соответствующих выборкам.
Подчеркнем, что
аналогичный вывод справедлив и для случая принадлежности равномерному закону.
При законах (4) с 
распределения статистики (1)
уже существенно отличаются от “классического”, соответствующего принадлежности
отсчетов нормальному закону.
При сильной
асимметричности закона распределения наблюдаемых случайных величин
распределение статистики (1) становится отличным от “классического”. На рис. 1 приведено
распределение статистики (1) также и для случая принадлежности показательному
(экспоненциальному) закону. Очевидно, что асимметричность закона влияет на
распределение статистики менее значимо, чем “тяжесть” хвостов. В случае
принадлежности асимметричным законам распределениям
экстремальных значений (минимального или максимального) распределения статистики
(1) практически не отличаются от “классического”.
Поведение распределения
статистики критерия Аббе было исследовано для
случаев, когда наблюдаемый закон представляет собой симметричную смесь законов
распределения. Например, когда закон распределения представляет собой смесь 2-х нормальных
законов вида
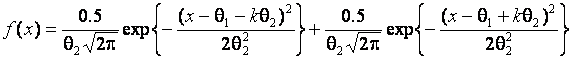. (5)
Построенные на основании
результатов моделирования распределения статистики критерия Аббе,
соответствующие случаям принадлежности смесям (5) со сдвигом компонент
смеси 
, 
и 
относительно 
, буквально накладываются одно на
другое и на распределение статистики при нормальном законе. Применение
критериев однородности Смирнова и Лемана-Розенблатта
[1,8] подтверждает вывод о практическом совпадении распределений.
Отсюда можно сделать вывод, что критерий Аббе не чувствителен (устойчив) к двумодальности закона распределения наблюдаемых величин при условии его симметричности и отсутствии тяжелых хвостов.
Исследование мощности критерия Аббе. В дальнейшем проверяемой гипотезе соответствует выполнение
предположений о независимости наблюдаемых величин и принадлежности их нормальному
закону с одинаковыми, но неизвестными дисперсиями. Без потери общности можно
рассматривать принадлежность стандартному нормальному
закону. В качестве конкурирующих гипотез рассматривались различные ситуации при
наличии тренда.
В случае линейного тренда моделировались случайные величины
,
(6)
относительно которых
проверялась гипотеза . В (6) 
представляют собой независимые
случайные величины, распределённые по стандартному нормальному закону, 
.
Величины 
(6) вычислялись в соответствии
с выражением 
, где шаг 
определялся как 
в зависимости от объема выборки
. Псевдослучайные величины генерировались в соответствии
со стандартным нормальным законом. Исследовалась мощность критерия относительно
альтернатив с линейным трендом, задаваемым параметром a=0,5; 1; 2; 3; 4. Соответствующие альтернативы
обозначены в дальнейшем как 
, 
, 
, 
, 
. Пример выборки, соответствующей
альтернативе при 
, представлен на рис. 2.
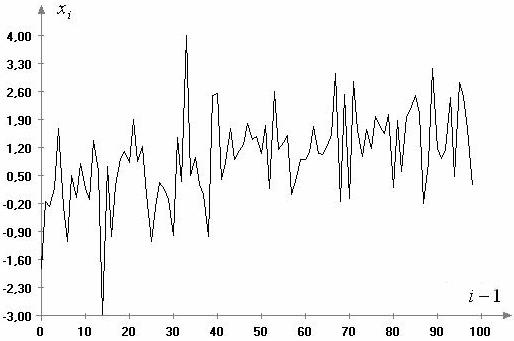
Рис.
2. Временной ряд, соответствующий модели (6) при 
и 
На рис. 3 представлены
построенные в результате моделирования эмпирические распределения 
статистики Аббе
при наличии линейного тренда в случае объема выборок 
. Значения мощности 
критерия Аббе,
где 
– вероятность ошибки второго рода, относительно
альтернатив , , , , с линейным трендом (6) в
зависимости от объема выборки при уровнях значимости 
приведены в таблице 3.
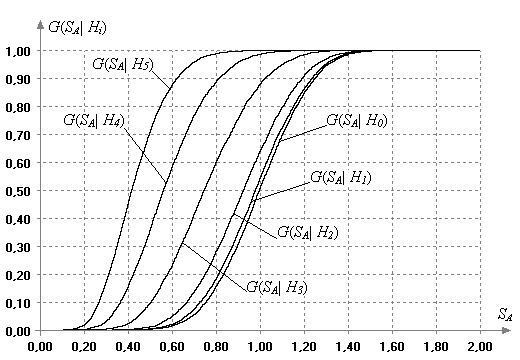
Рис. 3.
Распределения статистики критерия Аббе в случае
нормального закона и линейного тренда вида (6) при
Аналогичные исследования распределений статистики критерия Аббе и его мощности были проведены относительно альтернатив с периодическим трендом вида
,
(7)
где, как и в предыдущем случае, – независимые случайные величины распределённые по стандартному нормальному закону, , , а величины получались в соответствии с (7)
как 
.
Таблица 3. Мощность критерия Аббе при линейном тренде вида (6)
|
|
|
|
|
|
|
|
|
10 |
0,025 |
0,034 |
0,054 |
0,159 |
0,349 |
0,570 |
|
0,05 |
0,059 |
0,091 |
0,232 |
0,455 |
0,678 |
|
|
0,1 |
0,114 |
0,159 |
0,344 |
0,579 |
0,799 |
|
|
25 |
0,025 |
0,035 |
0,074 |
0,298 |
0,654 |
0,913 |
|
0,05 |
0,067 |
0,128 |
0,394 |
0,752 |
0,953 |
|
|
0,1 |
0,125 |
0,206 |
0,514 |
0,840 |
0,978 |
|
|
50 |
0,025 |
0,036 |
0,087 |
0,441 |
0,877 |
0,995 |
|
0,05 |
0,071 |
0,147 |
0,564 |
0,935 |
0,999 |
|
|
0,1 |
0,134 |
0,248 |
0,691 |
0,968 |
1 |
|
|
100 |
0,025 |
0,043 |
0,123 |
0,699 |
0,993 |
1 |
|
0,05 |
0,079 |
0,199 |
0,806 |
0,997 |
1 |
|
|
0,1 |
0,144 |
0,306 |
0,889 |
0,999 |
1 |
Исследовалась мощность
относительно альтернатив с нелинейным трендом (7), задаваемым параметром a=0,1; 0,25; 0,5; 1; 1,5;. Соответствующие альтернативы
обозначены в дальнейшем как 
, 
, 
, 
, 
. Пример выборки, соответствующей
альтернативе при , представлен на рис. 4.
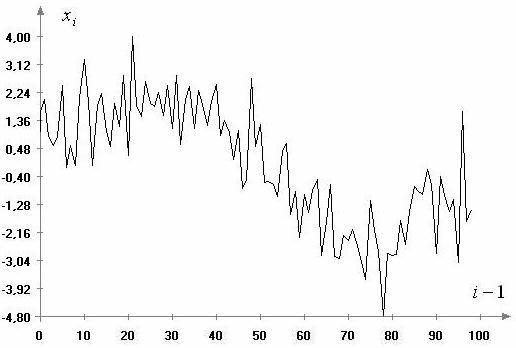
Рис.
4. Временной ряд, соответствующий модели (7) при и
Построенные в результате
моделирования эмпирических распределений статистики Аббе
при наличии нелинейного тренда (7) значения мощности критерия Аббе относительно альтернатив , , , , в зависимости от объема выборки
при уровнях значимости приведены в таблице 4.
Таблица 4. Мощность критерия Аббе при нелинейном тренде вида (7)
|
|
|
|
|
|
|
|
|
10 |
0,025 |
0,026 |
0,033 |
0,057 |
0,176 |
0,391 |
|
0,05 |
0,051 |
0,060 |
0,099 |
0,267 |
0,523 |
|
|
0,1 |
0,010 |
0,116 |
0,179 |
0,397 |
0,679 |
|
|
25 |
0,025 |
0,026 |
0,035 |
0,104 |
0,431 |
0,851 |
|
0,05 |
0,052 |
0,075 |
0,156 |
0,546 |
0,911 |
|
|
0,1 |
0,103 |
0,135 |
0,249 |
0,676 |
0,953 |
|
|
50 |
0,025 |
0,026 |
0,037 |
0,126 |
0,660 |
0,980 |
|
0,05 |
0,053 |
0,078 |
0,207 |
0,777 |
0,993 |
|
|
0,1 |
0,105 |
0,148 |
0,333 |
0,866 |
0,998 |
|
|
100 |
0,025 |
0,028 |
0,051 |
0,207 |
0,908 |
1 |
|
0,05 |
0,056 |
0,095 |
0,312 |
0,950 |
1 |
|
|
0,1 |
0,110 |
0,171 |
0,451 |
0,977 |
1 |
Ниже исследована мощность критерия относительно альтернатив с трендом вида
.
(8)
Были рассмотрены альтернативы 
, 
, 
, 
, 
, задаваемые параметром a=0,25; 0,5; 1; 1,5; 2, соответственно.
Полученные на основании
результатов моделирования оценки мощности относительно альтернатив , , , , с трендом вида (8) в
зависимости от объема выборки при уровнях значимости приведены в таблице 5.
Были проведены оценки
мощности критерия для альтернатив с линейным трендом вида (6) в случаях, когда подчинялись законам семейства
(4) с параметрами формы 
и 
при масштабном параметре 
. Оказалось, что в случае
распределения Лапласа () мощность относительно альтернатив , , , , ниже, чем при нормальном
законе, а при – выше. В рассмотренной
ситуации в случае распределения Лапласа мы имеем дисперсию большую, чем у
стандартного нормального закона, а в случае закона (4) с параметром формы – меньшую.
Таблица 5. Мощность критерия Аббе относительно альтернатив с трендом (8)
|
|
|
|
|
|
|
|
|
10 |
0,025 |
0,028 |
0,036 |
0,067 |
0,138 |
0,236 |
|
0,05 |
0,053 |
0,067 |
0,125 |
0,227 |
0,375 |
|
|
0,1 |
0,104 |
0,129 |
0,227 |
0,380 |
0,562 |
|
|
25 |
0,025 |
0,029 |
0,059 |
0,206 |
0,502 |
0,809 |
|
0,05 |
0,062 |
0,104 |
0,294 |
0,623 |
0,882 |
|
|
0,1 |
0,117 |
0,172 |
0,415 |
0,734 |
0,937 |
|
|
50 |
0,025 |
0,030 |
0,064 |
0,324 |
0,759 |
0,972 |
|
0,05 |
0,063 |
0,119 |
0,447 |
0,851 |
0,989 |
|
|
0,1 |
0,124 |
0,215 |
0,580 |
0,919 |
0,996 |
|
|
100 |
0,025 |
0,038 |
0,095 |
0,555 |
0,962 |
0,999 |
|
0,05 |
0,071 |
0,162 |
0,686 |
0,980 |
1 |
|
|
0,1 |
0,133 |
0,266 |
0,790 |
0,989 |
1 |
Исследование мощности против
тех же альтернатив при различных законах вида (4), но при одинаковых дисперсиях
величин , дало оценки мощности, практически совпадающие со
значениями, приведенными в таблице 2. Это свидетельствует о том, что на
распределение статистики критерия при справедливой конкурирующей гипотезе, а,
следовательно, и на мощность критерия практически не влияет вид закона, но
мощность критерия зависит от дисперсии наблюдаемых величин (ошибок измерений).
То есть, чем точнее измерения, тем выше мощность критерия, что вполне логично.
Выводы. Таким образом, на основании проведенных исследований, можно констатировать, что применение критерия Аббе будет корректным и в тех случаях, когда мы имеем дело с законом, существенно отличающимся от нормального. Однако закон не должен иметь “тяжелых” хвостов и быть симметричным. Закон может быть двумодальным, описываться симметричной смесью законов. В то же время умеренная асимметричность наблюдаемого закона практически не сказывается на распределении статистики критерия.
Полученные оценки мощности критерия позволяют судить о его способности обнаруживать наличие линейного и нелинейного тренда.
В качестве распределения
статистики критерия при можно применять нормальную аппроксимацию (2),
которая предпочтительней (3) и при больших .
Работа выполнена при поддержке Министерства образования и науки РФ (проекты № 15378 и № 02.442.11.7103) и РФФИ (проект № 06-01-00059).
1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
2. Neumann
J. von. Distribution of the ratio of the mean square successive difference to
the variance // AMS, 1941, 12. – p. 367-395.
3. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для ВУЗОВ – М.: ЮНИТИ, 1998. – 1022 с.
4. В.И. Струнов. О применении критерия Аббе для анализа независимости рядов измерений, характеризующихся отличными от нормального законами распределения // Измерительная техника (в печати).
5. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3. – С.3-15.
6. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.
7. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. – М.: Изд-во стандартов. 2002. – 64 с.
8. Лемешко Б.Ю., Лемешко С.Б. О сходимости распределений статистик и мощности критериев однородности Смирнова и Лемана-Розенблатта // Измерительная техника. 2005. № 12. – С.9-14.