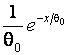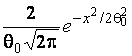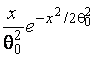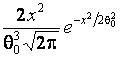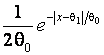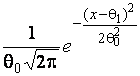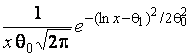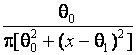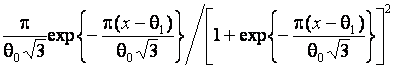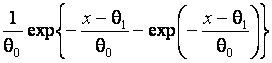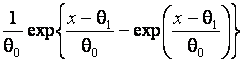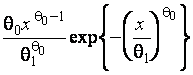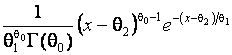Optoelectronics,
Instrumentation and Data Processing. 2001. - ą 2. - P. 76-88.
UDC
519.2
APPLICATION OF THE NONPARAMETRIC GOOGNESS-OF-FIT TESTS IN TESTING
COMPOSITE HYPOTHESES*
B.Yu. Lemeshko and S.N. Postovalov
1. Introduction
Testing
for fit of an obtained experimental distribution and a theoretical one of the
most common problems of statistical analysis in processing of experimental
results. Applying the goodness-of-fit tests, one distinguishes testing for
simple and composite hypotheses. A simple hypotheses tested has the form ![]() :
: ![]() , where
, where ![]() is the probability
distribution function to which the observed sample is tested for fit, and
is the probability
distribution function to which the observed sample is tested for fit, and ![]() is the known value of
the parameter (either scalar or vector one). A composite tested hypothesis has
the form
is the known value of
the parameter (either scalar or vector one). A composite tested hypothesis has
the form ![]() :
: ![]() . In this case, the estimate
of the distribution parameter
. In this case, the estimate
of the distribution parameter ![]() is calculated
by the same sample by which the fit is tested.
is calculated
by the same sample by which the fit is tested.
While testing the
fit by a sample we calculate the value ![]() of statistic
of the test used. To obtain the conclusion on accepting or rejecting the
hypothesis
of statistic
of the test used. To obtain the conclusion on accepting or rejecting the
hypothesis ![]() , we must know the
conditional distribution
, we must know the
conditional distribution ![]() of statistic
of statistic ![]() under validity of
hypothesis
under validity of
hypothesis ![]() . And if the
probability
. And if the
probability
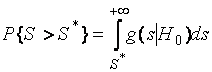
is
sufficiently great, at least ![]() ,
where
,
where ![]() is the conditional density, and
is the conditional density, and ![]() is the prescribed significance level (the probability of a
first-kind error – to reject the true hypothesis
is the prescribed significance level (the probability of a
first-kind error – to reject the true hypothesis ![]() ), then it is usually considered that there are no grounds for rejecting
the hypothesis
), then it is usually considered that there are no grounds for rejecting
the hypothesis ![]() .
.
The most commonly used goodness-of-fit tests include nonparametric Kolmogorov tests and also ![]() and
and ![]() Mises tests. The value
Mises tests. The value
![]() ,
,
where ![]() is the empirical
distribution function,
is the empirical
distribution function, ![]() is the
theoretical distribution function, and
is the
theoretical distribution function, and ![]() is the sample
size, is used as a distance between the empirical and theoretical laws in Kolmogorov test. For testing hypotheses, one usually uses
statistic of the form [1]
is the sample
size, is used as a distance between the empirical and theoretical laws in Kolmogorov test. For testing hypotheses, one usually uses
statistic of the form [1]
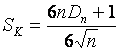 ,
,
where
![]() ,
, 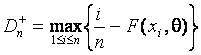 ,
, 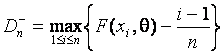 ,
,
![]() are sample values in increasing order, and
are sample values in increasing order, and ![]() is the distribution
function, fit to which is tested. The distribution of statistic
is the distribution
function, fit to which is tested. The distribution of statistic ![]() in testing the simple
hypothesis in the limit obeys Kolmogorov law
in testing the simple
hypothesis in the limit obeys Kolmogorov law ![]() [1].
[1].
In tests of the type of ![]() , the distance between the
hypothetical and the true distributions is considered in the quadratic metric
, the distance between the
hypothetical and the true distributions is considered in the quadratic metric
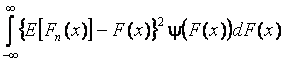 ,
,
where ![]() is the
mathematical expectation operator.
is the
mathematical expectation operator.
In choosing ![]() in Mises
in Mises ![]() tests, one
uses a statistic (Cramer – Mises – Smirnov statistic)
of the form
tests, one
uses a statistic (Cramer – Mises – Smirnov statistic)
of the form
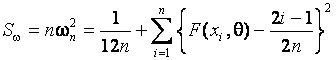 .
.
In testing a simple hypothesis
it obeys the distribution ![]() [1].
[1].
In choosing ![]() in Mises
in Mises ![]() tests, the
statistic (
tests, the
statistic (
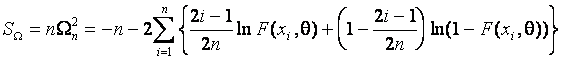 .
.
In the limit, this statistic
obeys the distribution ![]() [1].
[1].
In the case of simple hypotheses, the limiting statistic distributions of the
nonparametric Kolmogorov, ![]() and
and ![]() Mises
tests are known for a long time and do not depend on the kind of distribution law
observed and its parameters. These tests are said to be “distribution-free”
tests. This advantage predetermines common applications of these tests.
Mises
tests are known for a long time and do not depend on the kind of distribution law
observed and its parameters. These tests are said to be “distribution-free”
tests. This advantage predetermines common applications of these tests.
2. Losing the
“distribution–freeness” in testing composite hypotheses
While testing the composite hypotheses, when the same sample is used to
estimate the parameters of the observed law ![]() , the nonparametric goodness-of-fit tests lose the property of
“distribution–freeness”. However, the nonparametric test power in testing the
composite hypotheses for the same sample sizes is always much higher than that
in testing simple ones. And whereas in testing the simple hypotheses the
nonparametric Kolmogorov,
, the nonparametric goodness-of-fit tests lose the property of
“distribution–freeness”. However, the nonparametric test power in testing the
composite hypotheses for the same sample sizes is always much higher than that
in testing simple ones. And whereas in testing the simple hypotheses the
nonparametric Kolmogorov, ![]() and
and ![]() Mises tests have a lower power compared
with the
Mises tests have a lower power compared
with the ![]() -type tests provided that the latter use the asymptotically optimal
grouping [2-5], in testing the composite hypotheses the nonparametric
tests appear to be more powerful. To make use of their advantages, we must
merely know the distribution
-type tests provided that the latter use the asymptotically optimal
grouping [2-5], in testing the composite hypotheses the nonparametric
tests appear to be more powerful. To make use of their advantages, we must
merely know the distribution ![]() for
the tested composite hypotheses.
for
the tested composite hypotheses.
The distinctions in the limiting distributions of the same statistics in
testing simple and composite hypotheses are such significant that we cannot
neglect them. Hence, many publications [6-8] warned against inaccurate
application of the goodness-of-fit tests in testing composite hypotheses.
Paper [9] was the pioneer in investigating the limiting statistic
distributions of the nonparametric goodness-of-fit tests in testing the
composite hypotheses. The literature presents several approaches to using the
nonparametric goodness-of-fit tests in the case of testing the composite
hypotheses. When the size of a sample is large, it can be divided into two parts , and use one part for estimating the parameters and the
other part for testing the fit [10]. In some particular cases, the limiting
statistic distributions were analyzed analytically [11], the percent points of
the distributions were constructed by statistical simulation [12-15]. For
approximate calculation of the probabilities of “fit” of the form of ![]() (achievable significance level), some authors constructed formulas
that give sufficiently good approximations for small values of the
corresponding probabilities [16-20]. Authors of [21-24] investigated the
statistic distributions of the nonparametric goodness-of-fit tests and
constructed models of these distributions by means of computer analysis of statistical
regularities.
(achievable significance level), some authors constructed formulas
that give sufficiently good approximations for small values of the
corresponding probabilities [16-20]. Authors of [21-24] investigated the
statistic distributions of the nonparametric goodness-of-fit tests and
constructed models of these distributions by means of computer analysis of statistical
regularities.
It has been found that in composite hypotheses tests, the conditional
distribution law of the statistic ![]() is
affected by a number of factors determining the hypotheses complexity: the form
of the observed law
is
affected by a number of factors determining the hypotheses complexity: the form
of the observed law ![]() corresponding to the true hypothesis
corresponding to the true hypothesis ![]() ; the type of the parameter estimated and the number of parameters to be
estimated; sometimes, it is a concrete value of the parameter (e.g., in the
case of gamma-distribution); the method of parameter estimation.
; the type of the parameter estimated and the number of parameters to be
estimated; sometimes, it is a concrete value of the parameter (e.g., in the
case of gamma-distribution); the method of parameter estimation.
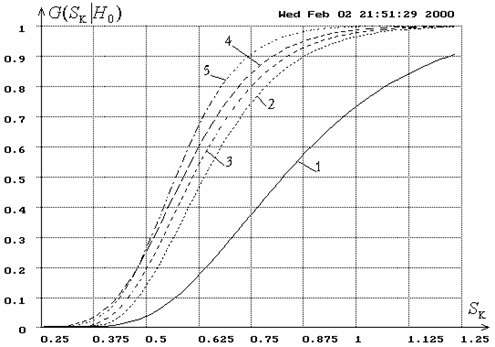
For example, Figure 1 illustrates ![]() as a function of form of the observed law
as a function of form of the observed law ![]() corresponding to hypothesis
corresponding to hypothesis ![]() for Kolmogorov test. Figure
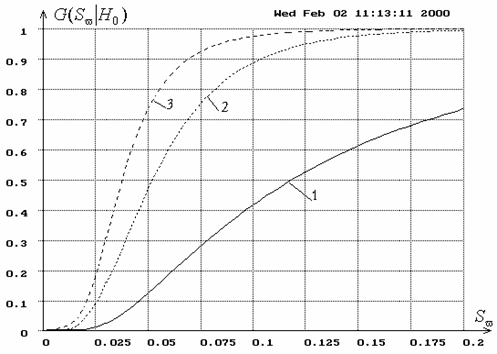
2 shows distributions of the Mises
for Kolmogorov test. Figure
2 shows distributions of the Mises ![]() statistic for test of fit to Weibull
distribution using various estimation methods: maximum likelihood estimates
(MLE) and minimum distance (MD) estimates obtained by minimizing the
value of the statistic used in the test.
statistic for test of fit to Weibull
distribution using various estimation methods: maximum likelihood estimates
(MLE) and minimum distance (MD) estimates obtained by minimizing the
value of the statistic used in the test.
Distributions of the goodness-of-fit statistics depend substantially on
the parameter estimation method. Strictly speaking, each type of estimates for
a concrete hypothesis tested is associated with its own limiting statistic distribution ![]() . Applying the nonparametric goodness-of-fit tests, one must consider
the estimation method used. For the maximum likelihood method the statistic
distributions
. Applying the nonparametric goodness-of-fit tests, one must consider
the estimation method used. For the maximum likelihood method the statistic
distributions ![]() depend strongly on the law corresponding to hypothesis
depend strongly on the law corresponding to hypothesis
![]() . The scatter of the distributions
. The scatter of the distributions ![]() when using MD estimates minimizing the test statistic is
much less dependent on the law
when using MD estimates minimizing the test statistic is
much less dependent on the law ![]() , corresponding to hypothesis
, corresponding to hypothesis ![]() .
.
For the MD estimates minimizing the test statistic, the empirical
distributions ![]() corresponding
to different hypotheses
corresponding
to different hypotheses ![]() have the
minimal scatter. Hence, we may speak about certain “distribution-freeness” for
the tests considered. If we use only this fact as a background, it would seem
that only such estimation methods must be applied for testing composite
hypotheses. However, investigation of the power of the tests considered using
different estimation methods has shown that for close alternatives the tests
have the greatest power in the case of using MLE.
have the
minimal scatter. Hence, we may speak about certain “distribution-freeness” for
the tests considered. If we use only this fact as a background, it would seem
that only such estimation methods must be applied for testing composite
hypotheses. However, investigation of the power of the tests considered using
different estimation methods has shown that for close alternatives the tests
have the greatest power in the case of using MLE.
Fig. 1.
Distribution functions ![]() of
statistic
of
statistic ![]() of Kolmogorov test:
of Kolmogorov test:
1 – for simple hypothesis testing; 2-5 – for
calculating MLE of two parameters of
Fig. 2.
Distribution functions ![]() of
statistic of the Mises
of
statistic of the Mises ![]() test for test of fit to Weibull
distribution: 1 – for simple hypothesis testing; 2 – for calculating MLE of two
parameters of the distribution; 3 – for calculating MD estimates of two
parameters.
test for test of fit to Weibull
distribution: 1 – for simple hypothesis testing; 2 – for calculating MLE of two
parameters of the distribution; 3 – for calculating MD estimates of two
parameters.
For small sample sizes the distributions ![]() depend on
depend on ![]() . However, we observe a substantial dependence of the statistic
distribution on
. However, we observe a substantial dependence of the statistic
distribution on ![]() only for small sample sizes. Investigation has shown, that for
only for small sample sizes. Investigation has shown, that for ![]() the distributions
the distributions ![]() are sufficiently close to the limiting
are sufficiently close to the limiting ![]() , and we may neglect the dependence on
, and we may neglect the dependence on ![]() .
.
3. Construction of
approximations for the limiting statistic distributions
The limiting statistic distributions of the nonparametric tests and
tables of the percent points constructed by the present moment are bounded by a
rather narrow range of composite hypotheses.
The infinite number
of random variables that can be met in practice cannot be described by a
limited subset of models of distribution laws that are most frequently used to
describe real observations. Any researcher can propose (construct) a parametric
distribution model of his own for a concrete observed variable, i.e., such a
model that describes most adequately this random variable, from his point of
view. Upon estimating by the given sample the model parameters, it becomes
necessary it test the hypothesis on adequacy of the sample observations and the
constructed law by means of the goodness-of-fit tests. The next problem
consists in knowledge of the limiting statistic distribution corresponding to
the given composite hypothesis.
Constructing of the
limiting distribution by analytical methods is an extremely complicated
problem. It is most suitable to use the method of computer analysis of
statistical regularities. The method showed good results in simulating the test
statistic distributions [21-24].
For this purpose,
we must according to the law ![]() simulate
simulate ![]() samples of the same size
samples of the same size
![]() as the sample
for which we must test hypothesis
as the sample
for which we must test hypothesis ![]() :
: ![]() , and then for each of
, and then for each of ![]() samples calculate
estimates of the same law parameters and the value of statistic
samples calculate
estimates of the same law parameters and the value of statistic ![]() of the corresponding
goodness-of-fit test. As a result, we will obtain a sample of values of
statistic
of the corresponding
goodness-of-fit test. As a result, we will obtain a sample of values of
statistic ![]() with the
distribution law
with the
distribution law ![]() for the hypotheses
for the hypotheses ![]() . With this sample
for a considerable number
. With this sample
for a considerable number ![]() we can
construct a sufficiently smooth empirical function of distribution
we can
construct a sufficiently smooth empirical function of distribution ![]() , that can be used in order to
conclude whether we must accept hypothesis
, that can be used in order to
conclude whether we must accept hypothesis ![]() . If it is necessary, using
. If it is necessary, using ![]() we can construct an
approximate analytical model approximating
we can construct an
approximate analytical model approximating ![]() , and then, on the basis of
this model, make the decision on the hypothesis tested.
, and then, on the basis of
this model, make the decision on the hypothesis tested.
Investigation has
shown that a good analytical model for ![]() is often
represented by one of the following laws: log-normal, gamma distribution, Su-Johnson
distribution, and Sl-Johnson distribution
[23-24]. At least, basing on the limiting number of distribution laws, we can
always construct a model in the form of a mixture of laws.
is often
represented by one of the following laws: log-normal, gamma distribution, Su-Johnson
distribution, and Sl-Johnson distribution
[23-24]. At least, basing on the limiting number of distribution laws, we can
always construct a model in the form of a mixture of laws.
Implementation of
such procedure of computer analysis of statistic distributions contains neither
difficulties of principal nor practical difficulties
at present. The level of computing allows one to obtain quickly results of
simulation, and an engineer who can write programs is able to implement the
algorithm. In this paper, we constructed models approximating the limiting
statistic distributions for some composite hypotheses with the use of MLE and MD
estimates.
Table 1 contains a list of distributions relative to
which we can test composite fit hypotheses using the constructed approximations
of the limiting statistic laws. The statistic distribution models constructed
by applying the method of computer analysis of statistical regularities are
presented in Tables 2–7 (Table 2, Table 3,
Table 4, Table 5, Table
6, Table 7). Tables of the models of the limiting
statistic distributions, including tables of percent points, for a wider class
of tested composite hypotheses are listed on WEB-site http://www.ami.nstu.ru/~headrd/seminar/nonparametric/start2.htm
[25].
Table 1
|
Random variable distribution |
Density function |
|
Exponential |
|
|
Seminormal |
|
|
Rayleigh |
|
|
Maxwell |
|
|
|
|
|
|
|
|
Log-normal |
|
|
Cauchy |
|
|
Logistic |
|
|
Extreme-value (maximum) |
|
|
Extreme-value (minimum) |
|
|
Weibull |
|
|
Gamma-distribution |
|
In tables 2–7, that contain the distributions ![]() recommended for testing
composite hypotheses,
recommended for testing
composite hypotheses, ![]() denotes the
log-normal distribution with the density function
denotes the
log-normal distribution with the density function
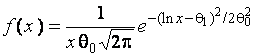 ,
,
![]() denotes
the gamma distribution with the density function
denotes
the gamma distribution with the density function
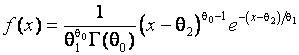 ,
,
![]() denotes
the Sl-Johnson distribution with the density
function
denotes
the Sl-Johnson distribution with the density
function
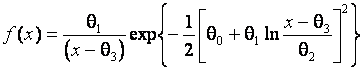 ,
,
![]() denotes the Su-Johnson distribution with the density
function
denotes the Su-Johnson distribution with the density
function
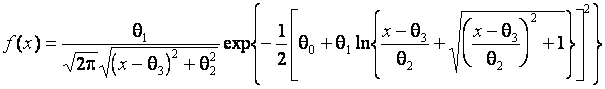 .
.
As an example, we will show how strong is the change in the probability ![]() for the same value of
statistic in the case of simple and composite hypotheses. For illustration, we
will use the Mises
for the same value of
statistic in the case of simple and composite hypotheses. For illustration, we
will use the Mises ![]() test.
test.
Example. Let we test a
hypotheses on fit to Weibull distribution and the
calculated statistic value ![]() . Hence, in the case of a
simple hypotheses on the basis of the distribution
. Hence, in the case of a
simple hypotheses on the basis of the distribution ![]() [1] we find, that
[1] we find, that ![]() . If using the sample we
calculate MLE of two distribution parameters, then a good approximation of the
limiting distribution (see Table 4) is the log-normal distribution lnN(-2.9541,0.5379), and the corresponding probability
. If using the sample we
calculate MLE of two distribution parameters, then a good approximation of the
limiting distribution (see Table 4) is the log-normal distribution lnN(-2.9541,0.5379), and the corresponding probability ![]() . For MD estimates in a
similar situation, the most suitable model (see Table 5) is the Su-Johnson
distribution Su(-1.5326, 1.4446, 0.0147, 0.0188) according to which
. For MD estimates in a
similar situation, the most suitable model (see Table 5) is the Su-Johnson
distribution Su(-1.5326, 1.4446, 0.0147, 0.0188) according to which ![]() .
.
4. Conclusion
To test composite hypotheses and choose (or construct) statistic
distributions ![]() of goodness-of-fit tests, one should take into account all factors
that affect the statistic distribution law: the form of the law observed; the
type of the parameter estimated and the number of the parameters; sometimes, a
concrete parameter value; the method of parameter estimation.
of goodness-of-fit tests, one should take into account all factors
that affect the statistic distribution law: the form of the law observed; the
type of the parameter estimated and the number of the parameters; sometimes, a
concrete parameter value; the method of parameter estimation.
The constructed approximations of the limiting statistic distributions
of the nonparametric goodness-of-fit tests extend the region of correct
application of these tests and may be recommended for construction of
statistical regularities when it is impossible to solve the problem
analytically.
References
1.
L.N. Bolshev and N.V.
Smirnov, Tables of Mathematical Statistics (in Russian), Nauka,
2.
V.I. Denisov, B.Yu. Lemeshko, and E.B. Tsoi, Optimal Grouping,
Parameter Estimation, and Design of Regression Experiments (in Russian), NSTU,
3.
B.Yu.
Lemeshko,
Nadezhnost i Kontrol Kachestva, no. 8, p.
3, 1997.
4.
B. Yu. Lemeshko, Zavod. Lab.,
vol. 64, no. 1, p. 56, 1998.
5.
V.I. Denisov, B.Yu. Lemeshko, and S.N. Postovalov, Application Statistics. Rules
for test of Fit of Experimental Distribution to Theoretical one.
Methodical Recommendations, Part 1. The Chi-squire Tests, NSTU,
6.
A.I. Orliv, Zavod. Lab.,
vol. 51, no. 1, p. 60, 1985.
7.
B. V. Bondarev, Zavod. Lab., vol. 52, no. 10, p. 62, 1986.
8.
E.V. Kulinskaya and N.E. Savvushkina, Zavod. Lab., vol. 56, no. 5, p. 96, 1990.
9.
Kac
M., Kiefer J., Wolfowitz J., Ann. Math. Stat., vol. 26, p. 189, 1955.
10. Durbin J., Lect. Notes Math., vol. 566,
p. 33, 1976.
11. G.V. Martynov, Omega-Square Tests (in Rissian), Nauka,
12.
E.S. Pearson, and H.O. Hartley, Biometrica
tables for Statistics, University Press,
13. M.A. Stephens, Journ.
14. M.A. Stephens, Journ. Amer. Statist.
Assoc., vol. 69, p. 730, 1974.
15. M. Chandra, N.D. Singpurwalla, and M.A.
Stephens, Journ. Amer. Statist.
Assoc., vol. 76, p. 375,
1981.
16. Yu. N. Tyurin, Izv.
AN SSSR. Ser. Mat. vol. 48, no.
6, p. 1314, 1984.
17. Yu. N. Tyurin, and N.E. Savvushkina,
Izv. AN SSSR. Ser. Tekhn. Kibernetika, no. 3, p. 109, 1984.
18. Yu. N. Tyurin, Author’s Abstracts of
Dissertation for Phys.-Math. Sci. Dr., MSU,
19. N.E. Savvushkina, Sb.
Trudov VNII Sistemnykh Issledovanii, no. 8, 1990.
20. Yu. N. Tyurin, and A.A. Makarov,
Computer Data Analysis (in Russian), INFRA-M, Finansi
i Statistika,
21. B.Yu. Lemeshko, and
S.N. Postovalov, Nadezhnost
i Kontrol Kachestva, no. 11, p. 3, 1997.
22. B.Yu. Lemeshko, and S.N. Postovalov,
Proc. of the IV Internat. Conf. on Actual Problems in
Electronics Instrument Building, Novosibirsk, vol. 3, p. 12, 1998.
23. B.Yu. Lemeshko, and S.N. Postovalov,
Zavod. Lab., vol. 64, no. 3, p. 61, 1998.
24. B.Yu. Lemeshko, and S.N. Postovalov,
Application Statistics. Rules for testing for Fit of
Experimental Distribution to Theoretical One. Methodical
Recommendations, Part II. Nonparametric Tests. (in Russian),
NSTU,
25. http://www.ami.nstu.ru/~headrd/
The
E-mail:
headrd@fpm.ami.nstu.ru
Table 2
|
Approximation of Limiting Kolmogorov Statistic Distributions when Maximum
Likelihood Estimates are Used |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
lnN(-0.3422,0.2545) |
|
|
|
Seminormal |
g(4.1332,0.1076,0.3205) |
|
|
|
Rayleigh |
lnN(-0.3388,0.2621) |
|
|
|
Maxwell |
lnN(-0.3461,0.2579) |
|
|
|
|
g(3.7580,0.1365,0.3163) |
g(4.6474,0.0870,0.3091) lnN(-0.3690,0.2499) |
g(4.4525,0.0761,0.3252) lnN(-0.4358,0.2276) |
|
|
g(3.7460,0.1385,0.3142) |
lnN(-0.4172,0.2272) |
g(4.9014,0.0691,0.2951) lnN(-0.4825,0.2296) |
|
Log-normal |
g(3.0622,0.1577,0.3547) |
Su(-2.0328, 2.3642, 0.2622, 0.4072) |
Su(-1.8093, 1.9041, 0.1861, 0.4174) |
|
Cauchy |
Su(-3.3278, 2.2529, 0.2185, 0.2858) |
g(4.8247,0.0874,0.2935) |
lnN(-0.5302,0.2427) |
|
Logistic |
g(3.2167,0.1476,0.3538) |
Su(-2.8534, 3.0657, 0.2872, 0.3199) |
lnN(-0.5611,0.2082) |
|
Extreme-value (maximum) |
g(3.3841,0.1439,0.3509) |
g(4.1008,0.0997,0.3269) |
g(4.9738,0.0660,0.3049) |
|
Extreme-value (minimum) |
g(3.3841,0.1439,0.3509) |
g(4.1008,0.0997,0.3269) |
g(4.9738,0.0660,0.3049) |
|
Weibull |
g(3.3841,0.1439,0.3509) ** |
g(4.1008,0.0997,0.3269) * |
g(4.9738,0.0660,0.3049) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.
Table 3
|
Approximation of Limiting
Distributions of Kolmogorov Minimum Statistic when MD Estimates
Minimizing Statistic SK are Used |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
g(4.4983,0.0621,0.2891) |
|
|
|
Seminormal |
g(4.2884,0.0705,0.3072) |
|
|
|
Rayleigh |
g(4.8579,0.0639,0.2900) |
|
|
|
Maxwell |
g(5.3106,0.0581,0.2865) |
|
|
|
|
g(3.0431,0.1355,0.3182) |
g(5.0103,0.0602,0.2968) lnN(-0.5358,0.2122) |
Su(-2.1079, 2.4629, 0.1661, 0.3340) lnN(-0.6970,0.1952) |
|
|
g(3.2458,0.1343,0.3072) |
lnN(-0.5469,0.2152) |
lnN(-0.7236,0.1837) |
|
Log-normal |
g(3.2458,0.1343,0.3072) |
lnN(-0.5469,0.2152) |
lnN(-0.7236,0.1837) |
|
Cauchy |
g(3.4398,0.1255,0.3022) |
lnN(-0.5182,0.2268) |
Su(-1.6929, 2.5234, 0.1892, 0.3607) lnN(-0.6946,0.1938) |
|
Logistic |
Su(-2.6522,1.8288, 0.1738, 0.3384) g(3.6342,0.1284,0.2772) |
Su(-3.8497, 3.2770, 0.2136, 0.2607) lnN(-0.5511,0.2045) |
lnN(-0.7389,0.1771) Su(-2.5093, 3.1277, 0.1932, 0.3041) |
|
Extreme-value (maximum) |
g(3.5424,0.1203,0.2975) |
Su(-1.9028, 2.3972, 0.2227, 0.389) |
Su(-1.3144, 2.2480, 0.1616,0.3858) lnN(-0.7174, 0.1841) |
|
Extreme-value (minimum) |
g(3.5424, 0.1203,0.2975) |
Su(-1.9028, 2.3972, 0.2227, 0.389) |
Su(-1.3144, 2.2480, 0.1616,0.3858) lnN(-0.7174, 0.1841) |
|
Weibull |
g(3.5424, 0.1203, 0.2975) ** |
Su(-1.9028, 2.3972, 0.2227, 0.389) * |
Su(-1.3144, 2.2480, 0.1616,0.3858) lnN(-0.7174, 0.1841) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.
Table 4
|
Approximation of Limiting
Distributions of Mises when Maximum
Likelihood Estimates are Used |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
Su(-1.8734,1.2118, 0.0223, 0.0240) |
|
|
|
Seminormal |
Sl(0.9735,1.1966, 0.1531, 0.0116) |
|
|
|
Rayleigh |
Su(-1.5302,1.0371, 0.0202, 0.0299) |
|
|
|
Maxwell |
Su(-2.0089,1.2557, 0.0213, 0.0213) |
|
|
|
|
Sl(0.9719,0.9805,0.2347, 0.0139) |
Su(-2.0821,1.2979, 0.0196, 0.0200) |
Su(-1.6085,1.2139, 0.0171, 0.0247) |
|
|
Su(-2.2550,0.9569, 0.0152, 0.0212) |
lnN(-2.7536,0.5610) |
lnN(-2.9794,0.5330) |
|
Log-normal |
Sl(1.0669,1.0010, 0.2537, 0.0144) |
lnN(-2.7271,0.6092) |
Su(-1.6292, 1.1541, 0.0144, 0.0234) |
|
Cauchy |
Sl(1.0086,1.0539, 0.2282, 0.0064) |
Sl(1.1230,1.2964, 0.1383, 0.0105) |
Sl(1.2420,1.2833, 0.1135, 0.0064) |
|
Logistic |
Sl(0.9982,1.0287, 0.2303, 0.0126) |
Sl(1.3982,1.3804, 0.1205, 0.0102) |
lnN(-3.1416,0.4989) |
|
Extreme-value (maximum) |
Sl(1.0056, 1.0452, 0.2296, 0.0137) |
lnN(-2.5818,0.6410) |
lnN(-2.9541,0.5379) |
|
Extreme-value (minimum) |
Sl(1.0056, 1.0452, 0.2296, 0.0137) |
lnN(-2.5818,0.6410) |
lnN(-2.9541,0.5379) |
|
Weibull |
Sl(1.0056, 1.0452, 0.2296, 0.0137) ** |
lnN(-2.5818,0.6410) * |
lnN(-2.9541,0.5379) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.
Table 5
|
Approximation of Limiting
Distributions of Mises when MD Estimates Minimizing
Statistic |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
Su(-1.9324,1.1610, 0.0134, 0.0203) |
|
|
|
Seminormal |
Su(-1.5024,1.0991, 0.0173, 0.0256) |
|
|
|
Rayleigh |
Su(-1.4705,1.1006, 0.0164, 0.0259) |
|
|
|
Maxwell |
Su(-1.7706,1.2978, 0.0188, 0.0220) |
|
|
|
|
Sl(1.0117, 0.9485, 0.2162, 0.0137) |
lnN(-2.8601,0.5471) |
lnN(-3.2853,0.4666) |
|
|
Sl(1.0477, 0.9883, 0.2356, 0.0112) |
lnN(-2.8649,0.5668) |
lnN(-3.2715,0.4645) |
|
Log-normal |
Sl(1.0477, 0.9883, 0.2356, 0.0112) |
lnN(-2.8649,0.5668) |
lnN(-3.2715,0.4645) |
|
Cauchy |
Sl(1.2759, 1.0437, 0.2825, 0.0089) |
lnN(-2.8577,0.5739) |
lnN(-3.2603,0.4874) |
|
Logistic |
Sl(1.0898,1.0225, 0.2399, 0.0096) |
lnN(-2.8831,0.5367) |
lnN(-3.2915,0.4592) |
|
Extreme-value (maximum) |
Sl(1.0771, 1.0388, 0.2065, 0.0109) |
Su(-1.5348,1.1226, 0.0166, 0.0252) |
Su(-1.5326, 1.4446, 0.0147, 0.0188) lnN(-3.2627,0.4680) |
|
Extreme-value (minimum) |
Sl(1.0771, 1.0388, 0.2065, 0.0109) |
Su(-1.5348,1.1226, 0.0166, 0.0252) |
Su(-1.5326, 1.4446, 0.0147, 0.0188) lnN(-3.2627,0.4680) |
|
Weibull |
Sl(1.0771, 1.0388, 0.2065, 0.0109) ** |
Su(-1.5348,1.1226, 0.0166, 0.0252) * |
Su(-1.5326, 1.4446, 0.0147, 0.0188) lnN(-3.2627,0.4680) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.
|
Approximation of Limiting
Distributions of Mises when Maximum Likelihood
Estimates are Used |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
Su(-2.8653,1.4220, 0.1050,0.1128) |
|
|
|
Seminormal |
Su(-2.5603,1.3116, 0.1147,0.1330) |
|
|
|
Rayleigh |
Su(-2.5610,1.4003, 0.1174,0.1337) |
|
|
|
Maxwell |
Su(-2.6064,1.4426, 0.1190,0.1285) |
|
|
|
|
Sl(0.3148, 1.0999, 0.6901, 0.1093) |
Su(-2.5528,1.4006, 0.1216,0.1358) |
Su(-2.8942,1.4897, 0.0846,0.1131) |
|
|
Su(-2.3507,1.0531, 0.1012,0.1595) |
Su(-3.1202,1.5233, 0.0874,0.1087) |
Su(-2.7057,1.7154, 0.1043,0.0925) |
|
Log-normal |
Su(-2.4168, 1.1296, 0.1151, 0.1560) |
lnN(-0.8052, 0.5123) |
Su(-2.3966, 1.5967, 0.1012, 0.1179) |
|
Cauchy |
Su(-2.4935, 1.0789, 0.0923, 0.1458) |
Su(-2.8420,1.3528, 0.1010,0.1221) |
Su(-2.3195,1.1812, 0.0769,0.1217) |
|
Logistic |
Sl(0.3065, 1.1628, 0.7002, 0.0930) |
Su(-3.5408,1.6041, 0.0773,0.0829) |
lnN(-1.1452,0.4426) |
|
Extreme-value (maximum) |
Su(-2.5427, 1.1057, 0.0960, 0.1569) |
Su(-2.5550, 1.3714, 0.1152, 0.1289) |
Su(-2.4622, 1.6473, 0.1075, 0.1149) |
|
Extreme-value (minimum) |
Su(-2.5427, 1.1057, 0.0960, 0.1569) |
Su(-2.5550, 1.3714, 0.1152, 0.1289) |
Su(-2.4622, 1.6473, 0.1075, 0.1149) |
|
Weibull |
Su(-2.5427, 1.1057, 0.0960, 0.1569) ** |
Su(-2.5550, 1.3714, 0.1152, 0.1289) * |
Su(-2.4622, 1.6473, 0.1075, 0.1149) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.
|
Approximation of
Limiting Distributions of Mises when MD Estimates
Minimizing Statistic |
|||
|
Random variable distribution |
Estimation of scale parameter |
Estimation of shift parameter |
Estimation of two parameters |
|
Exponential |
Su(-2.6741,1.4068, 0.0958,0.1230) |
|
|
|
Seminormal |
Su(-2.6752,1.3763, 0.0952,0.1280) |
|
|
|
Rayleigh |
Su(-2.2734,1.3473, 0.1101,0.1496) |
|
|
|
Maxwell |
Su(-2.2759,1.3988, 0.1171,0.1514) |
|
|
|
|
Su(-2.3884,1.0811, 0.0948, 0.1548) |
Su(-2.7267,1.4972, 0.1044,0.1239) |
Su(-2.4334,1.6104, 0.0902,0.1123) |
|
|
Su(-2.4180, 1.0702, 0.0957, 0.1464) |
Su(-2.7639, 1.5393, 0.1102, 0.1115) |
Su(-2.5746, 1.7505, 0.0979, 0.1043) lnN(-1.1651,0.4271) |
|
Log-normal |
Su(-2.4180, 1.0702, 0.0957, 0.1464) |
Su(-2.7639, 1.5393, 0.1102, 0.1115) |
Su(-2.5746, 1.7505, 0.0979, 0.1043) llnN(-1.1651,0.4271) |
|
Cauchy |
Su(-2.5043,1.1355, 0.1035,0.1384) |
Su(-2.7029,1.5179, 0.1188,0.1100) |
Su(-2.1046,1.4364, 0.0929,0.1301) lnN(-1.1043,0.4692) |
|
Logistic |
Sl(0.3223,1.1159,0.6836, 0.0953) Su(-2.3007,1.0135, 0.0906,0.1593) |
Su(-2.6212,1.4318, 0.0932,0.1370) |
Su(-3.0152,1.7751, 0.0800,0.0898) |
|
Extreme-value (maximum) |
Su(-2.4454, 1.1083, 0.0968, 0.1459) |
Su(-2.6557, 1.4282, 0.1024, 0.1254) |
Su(-2.1580, 1.5446, 0.0941, 0.1279) |
|
Extreme-value (minimum) |
Su(-2.4454, 1.1083, 0.0968, 0.1459) |
Su(-2.6557, 1.4282, 0.1024, 0.1254) |
Su(-2.1580, 1.5446, 0.0941, 0.1279) |
|
Weibull |
Su(-2.4454, 1.1083, 0.0968, 0.1459) ** |
Su(-2.6557, 1.4282, 0.1024, 0.1254) * |
Su(-2.1580, 1.5446, 0.0941, 0.1279) |
Note. ** - we estimated the Weibull distribution form parameter, * - the Weibull distribution scale parameter.