См. также: Прикладная математическая статистика (материалы к семинарам)

Измерительная техника. 2007. № 2. – С.22-27.

УДК 519.24

МОЩНОСТЬ КРИТЕРИЕВ СОГЛАСИЯ ПРИ БЛИЗКИХ АЛЬТЕРНАТИВАХ

Лемешко Б.Ю., Лемешко С.Б., Постовалов С.Н.

Методами статистического моделирования проведен анализ мощности ряда критериев согласия при проверке простых и сложных гипотез. Приведены оценки мощности критериев при проверке гипотез относительно некоторых близких альтернатив. Результаты позволяют упорядочить критерии по мощности.

Ключевые слова: критерий согласия, мощность критерия, критерий Колмогорова, критерий Крамера-Мизеса-Смирнова, критерий Андерсона-Дарлинга, критерий Пирсона, критерий Рао-Робсона-Никулина.

Критерии согласия предназначены для проверки гипотез о соответствии эмпирического распределения, построенного по выборке, извлекаемой из генеральной совокупности, некоторому теоретическому закону.

Различают проверку простых и сложных гипотез. Простая проверяемая гипотеза имеет вид : , где  – функция распределения вероятностей, с которой проверяют согласие наблюдаемой выборки, а  – известное значение параметра (скалярного или векторного).

Сложная проверяемая гипотеза может быть записана в виде : , где  – область определения неизвестного параметра . Отличие в применении критериев при проверке сложных гипотез и соответствующие проблемы возникают, если оценку параметра  теоретического распределения вычисляют по той же самой выборке, по которой проверяют согласие. Далее мы будем предполагать, что при проверке сложных гипотез оценка параметра  вычисляется по этой же выборке.

С проверкой статистических гипотез связывают ошибки двух видов. Ошибка 1-го рода заключается в том,  что в результате проверки отклоняется справедливая проверяемая гипотеза . Ошибка 2-го рода – в признании верной гипотезы , когда на самом деле справедлива некоторая конкурирующая гипотеза .

Процедура проверки гипотезы  предполагает, что известно распределение  статистики  применяемого критерия при справедливости . Для критериев согласия критические области определяются большими значениями статистик. Вероятность  ошибки 1-го рода (уровень значимости) представляет собой вероятность попадания значения статистики в критическую область: , где  – критическое значение.  При проверке гипотез величина , как правило, задается. Если вычисленное по выборке значение статистики ,  то проверяемая гипотеза  не отклоняется. Знание распределения  позволяет по значению  найти  – достигнутый уровень значимости. Проверяемая гипотеза  не отклоняется при .

Если задана конкурирующая гипотеза , то вероятность ошибки 2-го рода определяется соотношением , где  – распределение статистики критерия при справедливости . Если критерий полностью определен, то задание  однозначно определяет величину  и наоборот. Мощность критерия  при проверке гипотезы  относительно  представляет собой функцию, зависящую от , , объема выборки  и, возможно, от некоторых других факторов, связанных с построением критерия.

Отдавая при проведении статистического анализа данных предпочтение некоторому критерию, экспериментатор хотел бы иметь уверенность в том, что для заданной вероятности ошибки первого рода  гарантируется минимальная вероятность ошибки 2-го рода . Другими словами, хотелось бы отдать предпочтение критерию, наиболее мощному относительно интересующей нас пары альтернатив  и .

Информация, содержащаяся в различных источниках, о преимуществах в определенных ситуациях того или иного критерия согласия неоднозначна, зачастую противоречива и носит субъективный характер.

Исследования мощности затруднены отсутствием результатов, связанных с аналитическим представлением функций распределения  для конкретных критериев согласия при проверке сложных гипотез, в частности, для непараметрических критериев и для критериев типа  при оценивании параметров по точечным выборкам (по негруппированным наблюдениям).

Цель представленных в данной работе исследований заключалась в сравнительном анализе мощности наиболее часто используемых критериев согласия на некоторых парах достаточно близких конкурирующих гипотез  и . Интерес представляет способность критериев различать именно близкие гипотезы.

Наиболее часто в критерии Колмогорова [1] используют статистику с поправкой, предложенной Большевым [2], вида

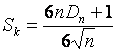,                                                    (1)

где

, , ,

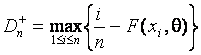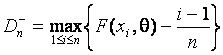 - объем выборки,  - упорядоченные по возрастанию выборочные значения. При справедливости простой проверяемой гипотезы статистика  в пределе подчиняется закону распределения Колмогорова  [1].

Статистика критерия Крамера-Мизеса-Смирнова имеет вид [1]

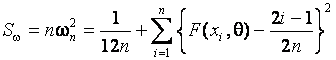.                        (2)

При справедливости простой гипотезы статистика в пределе подчиняется закону с функцией распределения  [1].

Статистика критерия Андерсона-Дарлинга определяется выражением [1]

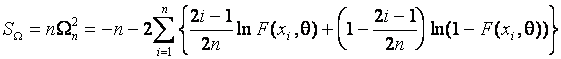   (3)

и при справедливости простой гипотезы в пределе подчиняется закону с функцией распределения  [1].

В случае проверки простых гипотез предельные распределения статистик данных непараметрических критериев не зависят от вида наблюдаемого закона распределения. В этой связи их называют “свободными от распределения”.

При проверке сложных гипотез, когда по этой же выборке оцениваются параметры закона, непараметрические критерии теряют свойство “свободы от распределения” [3]. Более того, при проверке сложных гипотез распределения статистик данных критериев определяются характером проверяемой сложной гипотезы [4].

Аналитический вид (предельных) распределений статистик  непараметрических критериев при проверке сложных гипотез неизвестен. Имеются частные решения, в основе которых использованы различные подходы. По-видимому, наиболее перспективным для построения распределений статистик является численный подход, базирующийся на статистическом моделировании эмпирических распределений статистик и последующем построении для них приближенных аналитических моделей [4-8].

Применение критерия Пирсона предусматривает разбиение области определения случайной величины на интервалов с подсчетом числа наблюдений , попавших в них, и вероятностей попадания в интервалы , соответствующих теоретическому закону. Статистика критерия имеет вид

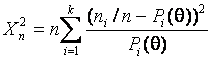.                                    (4)

В случае проверки простой справедливой гипотезы в пределе эта статистика подчиняется –распределению с  степенями свободы.

В случае проверки сложной гипотезы, при справедливости  и при условии, что оценки параметров находятся в результате минимизации статистики  (4) по этой же самой выборке, статистика  асимптотически распределена как , где  – число оцененных по выборке параметров. Статистика (4) имеет это же распределение, если в качестве метода оценивания выбирают метод максимального правдоподобия и оценки вычисляют по сгруппированным данным [9]. Более того, методами статистического моделирования было показано, что это имеет место, если используются и другие асимптотически эффективные оценки по группированным данным [10].

При вычислении оценок максимального правдоподобия (ОМП) по негруппированным данным эта же статистика подчиняется закону, отличному от -распределения. В этом случае при проверке сложных гипотез и использовании ОМП по негруппированным наблюдениям распределения  статистики критерия существенно зависят от способа группирования [11].

При подготовке [11] методами статистического моделирования были проведены исследования законов распределения статистик типа  в случае простых и различных сложных гипотез, при справедливости гипотезы  и справедливости конкурирующей гипотезы , при равновероятном (РВГ) и асимптотически оптимальном (АОГ) группировании [12]. При использовании АОГ минимизируются потери в информации Фишера, связанные с группированием, и максимизируется мощность критерия  Пирсона относительно близких конкурирующих гипотез.

Применение при проверке сложных гипотез с использованием критериев типа  оценок по негруппированным (точечным) наблюдениям имеет определенные преимущества. Такие оценки имеют лучшие асимптотические свойства по сравнению с оценками по группированным. К критериям такого вида относятся критерии со статистиками Рао-Робсона-Никулина [13]. Эти критерии обладают двумя преимуществами по отношению к критерию  Пирсона. Во-первых, замечательным фактом, отличающим эти критерии, является то, что статистика критерия при справедливости проверяемой гипотезы в пределе подчиняется -распределению независимо от числа параметров закона, оцененных методом максимального правдоподобия. Во-вторых, мощность критерия, как правило, выше мощности критерия  Пирсона.

В данном случае рассматривалась статистика, предложенная Никулиным [14-16]. Критерий предусматривает оценивание неизвестных параметров распределения  методом максимального правдоподобия по негруппированным данным. При этом вектор вероятностей попадания в интервалы  предполагается заданным, и граничные точки интервалов определяют по соотношениям , . Предложенная статистика имеет вид [14]

,                                (5)

где  вычисляется по формуле (4); матрица 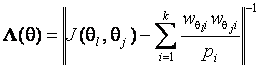, элементы и размерность которой определяются оцениваемыми компонентами вектора параметров ;  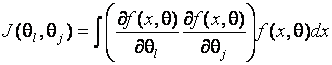– элементы информационной матрицы по негруппированным данным; компоненты вектора  имеют вид ;

.

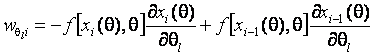При оценивании значений мощности критериев для построения эмпирических распределений   и  соответствующих статистик  наиболее целесообразно использование методов статистического моделирования. Для этого моделируются выборки статистик  достаточно большого объема  при конкретных объемах выборок  наблюдаемых величин, моделируемых по законам, соответствующим проверяемой  или конкурирующей  гипотезам. В дальнейшем, как правило,  величина , а индекс  в обозначениях соответствующих эмпирических функций опускается. Моделирование и исследование опиралось на развиваемое программное обеспечение задач статистического анализа.

Результаты сравнительного анализа мощности критериев согласия в данной работе иллюстрируются на двух парах альтернатив.

Первую пару составили нормальный и логистический законы: проверяемой гипотезе  соответствовал нормальный закон с плотностью

,

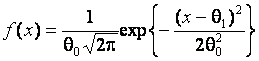а конкурирующей гипотезе  – логистический с функцией плотности

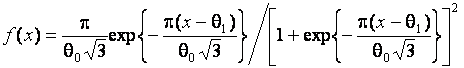
и параметрами , . В случае простой гипотезы  параметры нормального закона имеют те же значения. Эти два закона близки и трудно различимы с помощью критериев согласия.

Вторую пару составили:  – распределение Вейбулла с плотностью

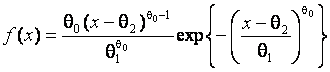
и параметрами , , ;  – гамма-распределение с плотностью

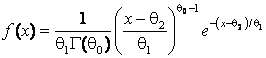
и параметрами , , , при которых гамма-распределение наиболее близко к данному распределению Вейбулла.

В работе исследовалась мощность при проверке простых и сложных гипотез  против простой альтернативы .

При проверке сложных гипотез и использовании всех исследуемых критериев согласия для оценивания неизвестных параметров применялся метод максимального правдоподобия. В этом случае, с одной стороны, все критерии оказываются в равных условиях. А с другой, непараметрические критерии типа Колмогорова, Крамера-Мизеса-Смирнова и Андерсона-Дарлинга при использовании ОМП являются более мощными по сравнению со случаем, когда оценки получаются в результате минимизации статистики соответствующего критерия [6].

Вычисленные на основании результатов моделирования распределений статистик оценки мощности рассматриваемых критериев согласия в случае пары альтернатив “нормальный-логистический” для различных значений уровня значимости  при проверке простой гипотезы , соответствующей нормальному закону с параметрами (0,1), против альтернативы , соответствующей логистическому закону с таким же набором параметров, приведены в таблице 1. Погрешность приводимых оценок мощности при проверке простых гипотез и 95% доверительном интервале не превышает величины . Критерии упорядочены по убыванию мощности.

В таблице 1 приведена максимальная мощность критерия  Пирсона, которую он имеет для данной пары альтернатив при  и АОГ.  При РВГ критерий  Пирсона относительно данной пары альтернатив имеет максимальную мощность при  [17]. А далее с ростом  мощность убывает. Но этот максимальный уровень мощности ниже мощности данного критерия при  с использованием АОГ.

Оценки мощности для случая проверки сложной гипотезы , соответствующей принадлежности наблюдаемой выборки нормальному закону, против той же простой конкурирующей гипотезы  представлены в таблице 2. Здесь также критерии упорядочены по убыванию мощности. Следует отметить, что в некоторых случаях предпочтительность неочевидна, так как, обладая большей мощностью при одних уровнях значимости и одних объемах выборок, критерий может проигрывать при других значениях  и . В таблице 2 указана максимальная мощность критериев Никулина и  Пирсона.

Таблица 1. Мощность критериев согласия при проверке простой гипотезы  (нормальное распределение) против альтернативы  (логистическое)

a	n=100	n=200	n=300	n=500	n=1000	n=2000
	Мощность критерия  Пирсона при k=15 и АОГ
0.15	0.349	0.459	0.565	0.737	0.946	0.999
0.1	0.290	0.388	0.490	0.671	0.922	0.998
0.05	0.210	0.292	0.385	0.565	0.871	0.996
0.025	0.154	0.222	0.302	0.472	0.813	0.992
0.01	0.107	0.159	0.221	0.369	0.729	0.983
	Мощность критерия Андерсона-Дарлинга
0.15	0.194	0.258	0.328	0.472	0.776	0.982
0.1	0.125	0.169	0.222	0.343	0.654	0.957
0.05	0.057	0.079	0.107	0.181	0.439	0.869
0.025	0.026	0.036	0.049	0.088	0.261	0.724
0.01	0.010	0.013	0.017	0.031	0.114	0.491
	Мощность критерия Колмогорова
0.15	0.190	0.246	0.303	0.415	0.662	0.922
0.1	0.127	0.170	0.215	0.309	0.544	0.861
0.05	0.062	0.088	0.116	0.179	0.365	0.721
0.025	0.031	0.044	0.061	0.100	0.231	0.560
0.01	0.012	0.018	0.026	0.044	0.119	0.366
	Мощность критерия Крамера-Мизеса-Смирнова
0.15	0.178	0.228	0.283	0.401	0.680	0.947
0.1	0.114	0.147	0.186	0.277	0.542	0.892
0.05	0.052	0.067	0.086	0.136	0.324	0.742
0.025	0.024	0.030	0.039	0.062	0.171	0.548
0.01	0.010	0.011	0.014	0.021	0.065	0.307

Оценивая мощность при проверке сложных гипотез, опирались на смоделированные распределения статистик  при  объеме выборок . При таких больших  эмпирическое распределение статистики может считаться хорошей оценкой предельного закона.

В случае проверки сложных гипотез и объемов выборок  и  для всех исследуемых критериев распределения  и  существенно отличаются от “предельного” при . Поэтому мощность оценивалась по смоделированным парам распределений вида ,  и , .

Таблица 2. Мощность критериев согласия при проверке сложной гипотезы  (нормальное распределение) против альтернативы  (логистическое)

a	n=20	n=50	n=100	n=200	n=300	n=500	n=1000	n=2000
	Мощность критерия Андерсона-Дарлинга
0.15	0.222	0.297	0.400	0.575	0.708	0.873	0.989	1.000
0.1	0.164	0.230	0.324	0.496	0.636	0.828	0.981	1.000
0.05	0.098	0.149	0.224	0.377	0.519	0.741	0.963	1.000
0.025	0.060	0.096	0.152	0.282	0.414	0.649	0.935	0.999
0.01	0.031	0.054	0.091	0.186	0.297	0.525	0.885	0.998
	Мощность критерия  Никулина при k=15 и АОГ
0.15	0.245	0.320	0.395	0.536	0.646	0.806	0.967	1.000
0.1	0.195	0.249	0.332	0.466	0.579	0.755	0.952	0.999
0.05	0.137	0.165	0.248	0.368	0.480	0.669	0.921	0.998
0.025	0.077	0.112	0.184	0.291	0.395	0.587	0.883	0.996
0.01	0.036	0.071	0.125	0.213	0.304	0.488	0.825	0.992
	Мощность критерия Крамера-Мизеса-Смирнова
0.15	0.210	0.273	0.366	0.529	0.659	0.836	0.980	1.000
0.1	0.153	0.208	0.291	0.447	0.582	0.781	0.968	1.000
0.05	0.090	0.130	0.194	0.329	0.458	0.678	0.939	0.999
0.025	0.053	0.082	0.128	0.237	0.353	0.573	0.897	0.998
0.01	0.027	0.044	0.074	0.150	0.243	0.445	0.825	0.994
	Мощность критерия  Пирсона при k=15 и АОГ
0.15	0.243	0.295	0.342	0.467	0.579	0.751	0.950	0.999
0.1	0.194	0.220	0.280	0.393	0.502	0.688	0.928	0.998
0.05	0.140	0.133	0.199	0.291	0.391	0.583	0.882	0.996
0.025	0.081	0.080	0.137	0.214	0.303	0.486	0.827	0.992
0.01	0.036	0.043	0.079	0.139	0.213	0.376	0.745	0.984
	Мощность критерия Колмогорова
0.15	0.200	0.246	0.313	0.440	0.554	0.732	0.941	0.999
0.1	0.142	0.181	0.236	0.351	0.459	0.646	0.905	0.997
0.05	0.080	0.105	0.143	0.230	0.322	0.502	0.823	0.990
0.025	0.045	0.061	0.086	0.149	0.219	0.376	0.721	0.975
0.01	0.021	0.029	0.043	0.081	0.127	0.244	0.575	0.938

Мощность критериев согласия при малых объемах выборок  можно сравнить с мощностью критериев, построенных специально для проверки отклонения распределения от нормального закона: с мощностью критериев Шапиро-Уилка, Эппса-Палли и Д’Агостино со статистикой . Оценки мощности данных критериев нормальности, полученные в [18] и уточненные в данной работе при объемах моделируемых выборок статистик , приведены в таблице 3. Как видим, “специальные” критерии относительно рассматриваемой пары альтернатив в среднем оказываются несколько мощнее.

Таблица 3. Мощность критериев проверки отклонения распределения от нормального закона (Шапиро-Уилка, Эппса-Палли и Д’Агостино со статистикой ) относительно альтернативы  (логистический закон)

a	Шапиро-Уилка		Эппса-Палли		Д’Агостино
	n=20	n=50	n=20	n=50	n=20	n=50
0.1	0.181	0.202	0.178	0.249	0.189	0.327
0.05	0.117	0.141	0.111	0.165	0.111	0.223
0.01	0.044	0.067	0.037	0.062	0.032	0.089

Вычисленные оценки мощности критериев для различных значений уровня значимости  при проверке согласия с распределением Вейбулла (гипотеза ) против альтернативы, соответствующей гамма-распределению с указанными параметрами (гипотеза ) при простой гипотезе  приведены в таблице 4, при сложной гипотезе  –  в таблице 5. Критерии в таблицах упорядочены по убыванию мощности.

Таблица 4. Мощность критериев согласия при проверке простой гипотезы  (распределение Вейбулла  с параметрами 2, 2, 0) относительно альтернативы  (гамма-распределение с параметрами 3.12154, 0.557706, 0)

a	n=100	n=200	n=300	n=500	n=1000	n=2000
	Мощность критерия  Пирсона при k=15 и АОГ
0.15	0.486	0.621	0.757	0.909	0.996	1.000
0.1	0.418	0.556	0.701	0.876	0.993	1.000
0.05	0.324	0.469	0.611	0.815	0.986	1.000
0.025	0.254	0.403	0.529	0.751	0.974	1.000
0.01	0.191	0.332	0.437	0.668	0.954	1.000
	Мощность критерия Андерсона-Дарлинга
0.15	0.302	0.446	0.577	0.781	0.976	1.000
0.1	0.223	0.348	0.473	0.689	0.951	1.000
0.05	0.131	0.224	0.326	0.533	0.882	0.998
0.025	0.076	0.141	0.220	0.396	0.785	0.993
0.01	0.037	0.075	0.126	0.257	0.636	0.975
	Мощность критерия Крамера-Мизеса-Смирнова
0.15	0.295	0.425	0.539	0.716	0.931	0.998
0.1	0.224	0.343	0.453	0.637	0.894	0.995
0.05	0.138	0.233	0.329	0.508	0.816	0.987
0.025	0.084	0.155	0.233	0.393	0.725	0.970
0.01	0.043	0.088	0.142	0.270	0.597	0.934
	Мощность критерия Колмогорова
0.15	0.294	0.421	0.531	0.700	0.915	0.995
0.1	0.225	0.342	0.450	0.628	0.879	0.992
0.05	0.141	0.237	0.332	0.508	0.806	0.981
0.025	0.087	0.160	0.239	0.401	0.723	0.964
0.01	0.045	0.093	0.150	0.282	0.606	0.930

Таблица 5. Мощность критериев согласия при проверке сложной гипотезы  (распределение Вейбулла 2, 2, 0) относительно альтернативы  (гамма-распределение с параметрами 3.12154, 0.557706, 0)

a	n=100	n=200	n=300	n=500	n=1000	n=2000
	Мощность критерия Андерсона-Дарлинга
0.15	0.435	0.667	0.817	0.952	0.999	1.000
0.1	0.353	0.589	0.757	0.928	0.998	1.000
0.05	0.244	0.466	0.650	0.876	0.995	1.000
0.025	0.167	0.361	0.547	0.811	0.990	1.000
0.01	0.100	0.252	0.424	0.715	0.977	1.000
	Мощность критерия Крамера-Мизеса-Смирнова
0.15	0.396	0.603	0.750	0.913	0.996	1.000
0.1	0.316	0.520	0.679	0.875	0.993	1.000
0.05	0.212	0.394	0.560	0.797	0.984	1.000
0.025	0.143	0.295	0.452	0.712	0.968	1.000
0.01	0.082	0.196	0.330	0.593	0.936	1.000
	Мощность критерия  Никулина при k=9 и АОГ
0.15	0.324	0.511	0.665	0.869	0.993	1.000
0.1	0.246	0.423	0.584	0.818	0.987	1.000
0.05	0.153	0.299	0.454	0.720	0.973	1.000
0.025	0.096	0.209	0.347	0.619	0.951	1.000
0.01	0.051	0.129	0.238	0.492	0.909	0.999
	Мощность критерия  Пирсона при k=9 и АОГ
0.15	0.347	0.525	0.678	0.868	0.992	1.000
0.1	0.273	0.439	0.596	0.818	0.986	1.000
0.05	0.172	0.311	0.463	0.719	0.970	1.000
0.025	0.104	0.218	0.352	0.617	0.946	1.000
0.01	0.053	0.133	0.237	0.483	0.898	0.999
	Мощность критерия Колмогорова
0.15	0.340	0.510	0.646	0.830	0.981	1.000
0.1	0.262	0.420	0.558	0.762	0.965	1.000
0.05	0.164	0.293	0.420	0.640	0.925	0.999
0.025	0.101	0.200	0.306	0.519	0.867	0.997
0.01	0.052	0.115	0.193	0.375	0.763	0.988

Таким образом, для случая проверки простых гипотез критерии можно упорядочить по мощности следующим образом:

 Пирсона (АОГ) Андерсона-Дарлинга Мизеса =Колмогорова

Такая шкала справедлива при использовании в критерии  Пирсона АОГ, при котором минимизируются потери в информации Фишера. При очень близких гипотезах может быть:

Колмогорова Мизеса.

При проверке сложных гипотез градация по мощности оказывается существенно иной:

Андерсона-Дарлинга Мизеса (АОГ)  Пирсона (АОГ)  Колмогорова.

При очень близких гипотезах может быть:

Андерсона-Дарлинга (АОГ) Мизеса  Пирсона (АОГ)  Колмогорова.

Указанные выводы носят интегрированный характер. Такое упорядочение не является жёстким. Как видно из таблиц с приведенными значениями мощности, иногда критерий имеет преимущества по мощности при одних значениях  и объемах выборок  и уступает при других значениях  и .

Надо иметь в ввиду, что мощность критериев типа  (Пирсона и Никулина) зависит не только от гипотез ,  и объема выборок , но при заданных  и  − от способа группирования и числа интервалов.

Число интервалов, при котором мощность критериев для пары альтернатив  и  максимальна, зависит от этих гипотез и от способа группирования. Увеличение числа интервалов не всегда приводит к росту мощности критериев типа  [17].

При близких гипотезах  и  выбор АОГ при использовании критерия  Пирсона дает положительный эффект как при простых, так и при сложных гипотезах. Однако это не означает, что использование АОГ всегда гарантирует максимальную мощность данного критерия. При конкретных и не очень близких гипотезах оптимальным может оказаться некоторый другой способ группирования, который может быть найден в результате максимизации мощности критерия.

Вывод о безоговорочно положительном эффекте применения АОГ нельзя распространять на критерий Никулина: при одной и той же паре гипотез  и  при одном числе интервалов  критерий оказывается более мощным при АОГ, при другом  − более мощным при РВГ. Зависимость мощности от способа группирования  оказывается более сложной и требует исследования.

Работа выполнена при поддержке Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119) и РФФИ (проект № 06-01-00059-а).

Литература

1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

2. Большев Л.Н. Асимптотические пирсоновские преобразования // Теория вероятностей и ее применения. 1963. – Т. 8. – № 2. – С. 129-155.

3. Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat. 1955. – V.26. – P.189-211.

4. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. - М.: Изд-во стандартов. 2002. - 64 с.

5. Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. 1998. – Т. 64. – № 3. – С. 61-72.

6. Лемешко Б.Ю., Постовалов С.Н. О зависимости распределений статистик непараметрических критериев и их мощности от метода оценивания параметров // Заводская лаборатория. Диагностика материалов. 2001. – Т. 67. – № 7. – С. 62-71.

7. Лемешко Б.Ю., Постовалов С.Н. Применение непараметрических критериев согласия при проверке сложных гипотез // Автометрия. 2001. – № 2. – С. 88-102.

8. Лемешко Б.Ю., Маклаков А.А. Непараметрические критерии при проверке сложных гипотез о согласии с распределениями экспоненциального семейства // Автометрия. 2004. №3. – С. 3-20.

9. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.

10. Лемешко Б.Ю., Чимитова Е.В. Оптимальные L-оценки параметров сдвига и масштаба распределений по выборочным квантилям // Заводская лаборатория. Диагностика материалов. 2004. – Т.70. – №1. – С. 54-66.

11. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.

12. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория. 1998. – Т. 64. – №1. – С. 56-64.

13. Van der Vaart A.W. Asymptotic Statistics. – Cambridge University Press. 1998. –443 p.

14. Никулин М.С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и ее применение. – 1973. – Т. XVIII. – № 3. – С.675-676.

15. Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // Заводская лаборатория. 1992. – Т. 58. – № 3. – С.52-58.

16. Greenwood P.E., Nikulin M.S. A Guide to Chi-Squared Testing. – John Wiley & Sons, Inc. 1996. – 280 p.

17. Лемешко Б.Ю., Чимитова Е.В. О выборе числа интервалов в критериях согласия типа c² // Заводская лаборатория. Диагностика материалов. 2003. – Т. 69. – № 1. – С. 61-67.

18. Лемешко Б.Ю., Лемешко С.Б. Сравнительный анализ критериев проверки отклонения распределения от нормального закона // Метрология. 2005. – №2. – С. 3-24.