См. также: Прикладная математическая статистика (материалы к семинарам)

Метрология. 2007. – № 5. – С. 3-13

519.245: 006.91.001

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КАК ЭФФЕКТИВНЫЙ ИНСТРУМЕНТ ДЛЯ ИССЛЕДОВАНИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН

Лемешко Б.Ю., Огурцов Д.В.

На основании разработанного программного обеспечения методами статистического моделирования исследуются законы распределения вероятностей различных функций от случайных величин, подчиняющихся различным одномерным законам распределения. Показывается эффективность методики при исследовании вероятностных закономерностей.

Ключевые слова: статистическое моделирование, функция случайных величин, закон распределения функции случайных величин.

Достаточно часто решаемой задачей в метрологии является задача определения вероятностных характеристик величины , непосредственно недоступной для измерения, на основании доступных для многократных измерений величин , , …, , если известна функция

,

или в векторной форме , а совместное распределение вероятностей входных переменных , , …,  найдено на основании результатов статистического анализа.

Классический подход [1,2] определения закона распределения вероятностей функции от системы случайных величин предполагает знание совместной плотности распределения  системы случайных величин , , …, . Однако аналитическое решение с помощью классического подхода удается найти только для некоторых частных случаев  и  [2].

Вследствие этого при определении вероятностных характеристик выходной переменной модели  в случае некоррелированности входных переменных , , …,  рекомендуется [3] линеаризация модели

,                         (1)

где  – вектор математических ожиданий ,  – градиент функции.

Такой подход позволяет достаточно просто на основании законов распределения входных переменных , , …,  или их числовых характеристик определить соответствующие характеристики случайной величины . К сожалению, данный подход оказывается эффективным также в относительно редких случаях при близости функции к линейной.

В [4] на примере функции  демонстрируется различие в решениях, полученных при использовании классического подхода и в результате линеаризации, подчеркиваются недопустимо большие погрешности, к которым приводит применение метода линеаризации.

Тем не менее, метод линеаризации широко используют на практике, в том числе в информационно-измерительных системах (ИИС), осуществляющих косвенные измерения. Например, в [5] данный подход используется для исследования метрологических характеристик многоканальных ИИС с мультипликативной связью между каналами. В результате линеаризации мультипликативное взаимодействие каналов заменяется на аддитивное. Следует ожидать, что применение такого приема в ситуации, описываемой в [5] должно приводить к заниженным оценкам погрешности измерений.

Что же делать: аналитическое решение в соответствии с классическим подходом в большинстве реальных ситуаций получить не удается, а линеаризация приводит к неадекватным решениям? Цель данной работы – обратить внимание метрологов на эффективность метода статистических испытаний для исследования вероятностных закономерностей, на его возможности при построении вероятностных моделей для функций от случайных величин, для уточнения вероятностных характеристик погрешностей при косвенных измерениях. К сожалению, в отечественных работах метод статистических испытаний незаслуженно редко используется для исследования вероятностных закономерностей.

Для исследования законов распределения функций от случайных величин было разработано программное обеспечение, позволяющее моделировать выборки функций от случайных величин. Интерфейс с пользователем позволяет задавать произвольные функции от системы независимых (пока) случайных величин, распределенных по различным одномерным законам.

 Рассмотрим несколько примеров, демонстрирующих точность статистического моделирования и его эффективность при исследовании поведения законов распределения  функций от случайных величин

Очевидно, что распределение функции  существенно зависит от вида тех законов, которым подчинены случайные величины , от области их определения. Более того, функция  от , распределенных по одним и тем же законам, может описываться очень различающимися моделями вероятностных законов в зависимости от параметров законов, описывающих случайные величины . Покажем это на функции  в случае принадлежности  нормальным законам.

Пример 1. , где  и независимы. Теоретическим законом распределения  является стандартное распределение Коши с плотностью 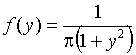, . В таблице 1 приведены результаты проверки согласия смоделированной выборки величины  с распределением Коши. В этом и в остальных случаях объёмы моделируемых выборок составили 10000 значений. В случае критерия  Пирсона использовано асимптотически оптимальное группирование, обеспечивающее максимальную мощность относительно близких конкурирующих гипотез [6]. В таблице приведены значения статистик применяемых критериев согласия, вычисленные по выборке, и  достигнутые уровни значимости по каждому критерию [6, 7]. Достигнутый уровень значимости представляет собой вероятность , где  – значение статистики  соответствующего критерия, вычисленное по выборке. Гипотеза о согласии эмпирического распределения с теоретическим по соответствующему критерию отклоняется, если , где  – заданная вероятность ошибки 1-го рода.  В данном случае достигнутые уровни значимости по всем применяемым критериям свидетельствуют об очень хорошем согласии полученного в результате моделирования эмпирического распределения с распределением Коши.

Таблица 1. Результаты проверки согласия выборки величины  со стандартным распределением Коши в случае .

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	12.547	0.5625
Колмогорова	0.6087	0.8526
Мизеса	0.0521	0.8636
Андерсона-Дарлинга	0.3416	0.9040

Пример 2. , где ,  и независимы. Теоретическим законом распределения  является распределение Коши с плотностью 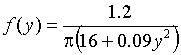, . Результаты проверки согласия смоделированной выборки с распределением Коши приведены в таблице 2.

Таблица 2. Результаты проверки согласия выборки величины  с распределением Коши в случае , .

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	10.713	0.7084
Колмогорова	0.7169	0.6829
Мизеса	0.0530	0.8577
Андерсона-Дарлинга	0.3202	0.9222

Пример 3. , где  и независимы. В случае  и  законом распределения  уже не является распределение Коши. Оценивание параметров плотности Коши 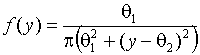 по смоделированной выборке дает оценки максимального правдоподобия (ОМП) параметров масштаба =0.7895 и сдвига =0.6150. Оценка параметра сдвига совпадает с медианой эмпирического распределения. Проверка согласия полученного в результате моделирования эмпирического распределения с законом распределения Коши отклоняется по всем критериям. Это является следствием того, что действительное распределение величины  в данном случае стало явно асимметричным.

В общем случае плотность распределения частного при ,  может быть представлена в виде [8, 9]:

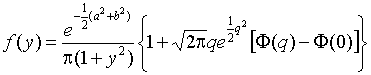,                  (2)

где , а  – функция распределения стандартного нормального закона. Результаты проверки согласия смоделированной выборки с распределением (2)  при ,  приведены в таблице 3.

Таблица 3. Результаты проверки согласия выборки величины  с распределением, полученным по формуле (2), в случае , .

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	17.406	0.2351
Колмогорова	0.8085	0.5302
Мизеса	0.1462	0.4012
Андерсона-Дарлинга	0.9025	0.4126

Пример 4. , где ,  и независимы. В случае существенного превышения абсолютного значения параметра сдвига величины  над сдвигом  хорошей моделью для  является нормальное распределение. На рисунке 1 представлены гистограмма, построенная по эмпирическому распределению при 15 интервалах и асимптотически оптимальном группировании [6, 10], и плотность нормального распределения с оценками параметров масштаба =0.10051 и сдвига = 0.10067. В таблице 4 приведены результаты проверки согласия смоделированной выборки с нормальным распределением.

Таблица 4. Результаты проверки согласия выборки величины  с нормальным распределением в случае ,

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	23.272	0.0255
Колмогорова	0.6501	0.3991
Мизеса	0.0870	0.1564
Андерсона-Дарлинга	0.6545	0.0827

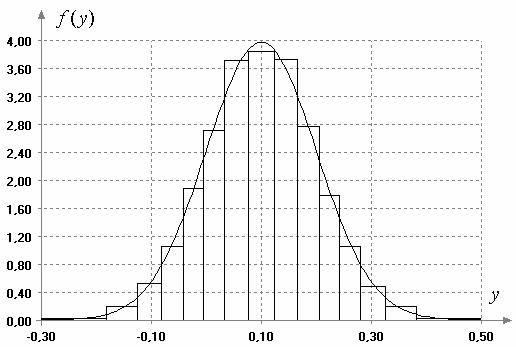
Рис. 1. Плотность и гистограмма распределения при ,

В рассматриваемом примере плотность  имеет вид (2) при , . Результаты проверки согласия смоделированной выборки с распределением (2) приведены в таблице 5.

Таблица 5. Результаты проверки согласия выборки величины  с распределением (2), в случае ,

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	17.023	0.2549
Колмогорова	0.9115	0.3770
Мизеса	0.1462	0.4012
Андерсона-Дарлинга	1.0833	0.3163

Данный пример для функции  это случай, когда применение линеаризации оказывается правомерным. Линеаризация дает нормальное распределение с математическим ожиданием 0.1 и дисперсией 0.0101, то есть нормальное с параметрами масштаба =0.1 и сдвига =0.100499, что не так уж далеко от истинного положения вещей.

С ростом абсолютной величины параметра сдвига  по отношению к сдвигу  распределение  стремится к нормальному (при равенстве дисперсий). С ростом дисперсии  распределение  начинает отклоняться от нормального. В этих же условиях при росте дисперсии  по отношению к дисперсии  распределение хорошо аппроксимируется нормальным законом. А применение линеаризации в этом случае приводит к нормальному закону с более заметным смещением относительно истинного закона распределения.

Когда стандартное отклонение  много меньше его математического ожидания и распределения  близки к нормальному, распределение  хорошо аппроксимируется нормальным законом и линеаризация также дает хорошие результаты.

Пример 5. , где ,  и независимы. Плотность распределения  в данном случае имеет вид (2) при , . Результаты проверки согласия смоделированной выборки с распределением (2) приведены в таблице 6. Вид эмпирической функции распределения, полученной при моделировании, представлен на рис. 2. Очевидно, что ее хорошо можно описать некоторой смесью распределений, аналитический вид которой отличен от закона (2).

Таблица 6. Результаты проверки согласия выборки величины  с распределением (2) в случае ,

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	14.927	0.3831
Колмогорова	0.8050	0.5359
Мизеса	0.1261	0.4710
Андерсона-Дарлинга	0.92532	0.3989

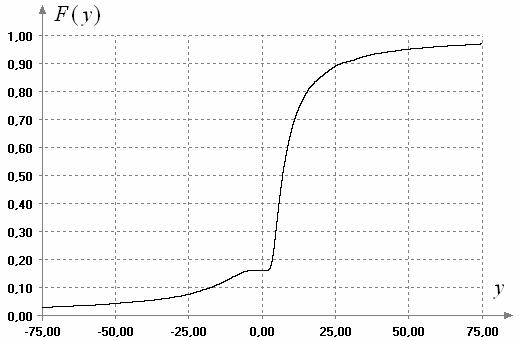
Рис. 2. Эмпирическое распределение при ,

В [5] применение линеаризации предусматривается для закона распределения произведения случайных величин. Насколько будет правомерно применение линеаризации в подобном случае?

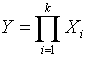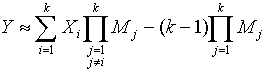Пусть , где  – взаимно некоррелированные случайные величины с математическим ожиданием  и дисперсией . В соответствии с (1) , математическое ожидание  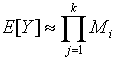и дисперсия .

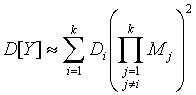Распределения произведений исследовались при различных законах распределения .

В случае принадлежности  стандартным нормальным законам для применение линеаризации невозможно по очевидной причине: дисперсия оказывается нулевой. Полученные в результате моделирования распределения  в данном случае представляют собой асимметричные законы с нулевой медианой. Эти распределения не удается адекватно описать какой-то одной параметрической моделью закона, однако они достаточно хорошо аппроксимируются смесями вида:

.

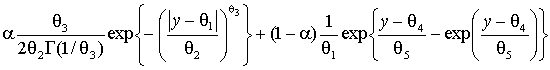В таблице 7 для данного случая приведены реальные доверительные интервалы для , подчеркивающие асимметричность законов.

Таблица 7. Доверительные интервалы для произведения  нормальных стандартных случайных величин

	90% доверительный интервал	95% доверительный интервал
1	-1.645;  1.645	-1.960;  1.960
2	-1,627;  1,603	-2,185;  2,167
3	-1,314;  1,356	-1,980;  2,057
4	-1,053;  1,116	-1,836;  1,934
5	-0,868;  0,749	-1,463;  1,296

На рис. 3 представлены эмпирические распределения аналогичных произведений случайных величин, но принадлежащих нормальному закону с параметрами сдвига и масштаба, равными единице. Распределения  для этого случая при  неплохо описываются смесями двух, а при  – трех параметрических моделей. Различие между реальными доверительными интервалами и полученными в результате линеаризации демонстрируется в таблице 8.

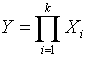При повышении точности измерений  (с уменьшением ) распределение  стремится к нормальному закону. Например, при  и  распределение  хорошо согласуется с нормальным законом N(0.99973, 0.02232), построенным по смоделированной выборке. В этом случае линеаризация дает идентичные результаты: N(1, 0.02236). То же самое наблюдается с ростом  при постоянстве .

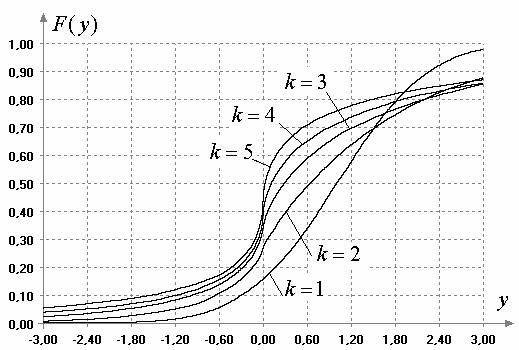
Рис.3. Эмпирические распределения произведений  нормальных величин с параметрами сдвига и масштаба, равными единице

Таблица 8. Доверительные интервалы для произведения  нормальных случайных величин с параметрами сдвига и масштаба, равными единице

	90% доверительный интервал		95% доверительный интервал
	Реальный	Линеаризованный	Реальный	Линеаризованный
1	-0.645; 2.645	-0.645; 2.645	-0.960; 2.960	-0.960; 2.960
2	-1.191; 4.360	-1,326; 3,326	-1.828; 5.293	-1,772; 3,772
3	-1.870; 6.104	-1,849; 3,849	-2.850; 8.375	-2,395; 4,395
4	-2.419; 7.540	-2,290; 4,290	-4.158; 10.942	-2,920; 4,920
5	-3.157; 8.483	-2,678; 4,678	-5.620; 13.793	-3,383; 5,383

В заключение проиллюстрируем, насколько хорошие модели можно строить для произвольных функций от систем случайных величин. Например, для функции , где , , , , , т.е. принадлежат нормальному, равномерному и экспоненциальному законам, с указанными параметрами сдвига и масштаба, очень хорошей моделью оказывается распределение с плотностью

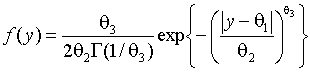                       (3)

и оценками параметров =0.0014, =0.4461, =0.7922. О степени близости полученного эмпирического распределения к теоретическому (3) свидетельствуют высокие достигнутые уровни значимости по применяемым критериям согласия (при проверке сложных гипотез [6, 7]), представленные в таблице 9.

Таблица 9. Результаты проверки согласия с распределением (3) выборки значений функции

Критерий	Значение статистики	Достигнутый уровень значимости
Пирсона при	15.064	0.1796
Колмогорова	0.4796	0.8847
Мизеса	0.0423	0.7028
Андерсона-Дарлинга	0.3647	0.6035

Таким образом, методы статистического моделирования в совокупности с программным обеспечением, позволяющим строить приближенные математические модели для полученных эмпирических распределений (в том числе в виде смесей различных параметрических законов), представляют собой эффективный инструмент для изучения законов распределения функций от случайных величин, для исследования вероятностных закономерностей, проявляющихся в задачах метрологии.

Распределения функций от случайных величин  зависят не только от вида законов распределений  и могут меняться в широких пределах в зависимости от параметров этих законов. Используя методы статистического моделирования для исследования закона распределения , можно либо построить приближенную модель, аппроксимирующую этот закон в конкретном случае, либо выяснить условия, обеспечивающие обоснованность применения линеаризации.

Повышение точности измерений  в определенных условиях, хотя и далеко не всегда, способствует тому, что распределение величины , представляющей собой функцию , становится ближе к нормальному закону.

Использование статистического моделирования и специализированного программного обеспечения, примером которого является развиваемая система “Интервальная статистика” ISW [11], позволяет строить хорошие приближенные математические модели законов распределения функций случайных величин (в том числе, в форме смесей параметрических моделей законов),  когда этот закон не удается найти аналитически.

Работа выполнена при поддержке РФФИ (проект № 06-01-00059-а) и Министерства образования и науки РФ (проект № 2006-РИ-19.0/001/119).

Литература

1. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982. – 256 с.

2. Гурский Е.И. Теория вероятностей с элементами математической статистики. – М.: Высшая школа, 1971. – 328 с.

3. МИ 2083-90. ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей.

4. Левин С.Ф. Схема приведения в методе косвенного измерения // Измерительная техника, 2004. – № 3. – С.5-9.

5. Шевчук В.П., Лясин Д.Н. Количественная оценка погрешности измерений обобщенных технологических параметров // Измерительная техника, 2004. – № 10. – С.16-20.

6. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.

7. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. - М.: Изд-во стандартов. 2002. - 64 с.

8. Marsaglia G. Ratios of Normal Variables and Ratios of Sums of Uniform Variables // Journal of the American Statistical Association. 1965. – V.60. – P.193–204.

9. Marsaglia G. Ratios of Normal Variables // Journal of Statistical Software. 2006. – V.16. Issue 4. URL http://www.jstatsoft.org/v11/i04/.

10. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория. 1998. – Т. 64. – №1. – С. 56-64.

11. Лемешко Б.Ю., Постовалов С.Н. Компьютерные технологии анализа данных и исследования статистических закономерностей. – Новосибирск: Изд-во НГТУ, 2004. – 119 с.