См. также: Прикладная математическая статистика (материалы к семинарам)

 

Измерительная техника. 2004. № 2. С. 15-20

УДК 519.25

 

ОБ ОШИБКАХ, СОВЕРШАЕМЫХ ПРИ ИСПОЛЬЗОВАНИИ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СОГЛАСИЯ[1]

 

Лемешко Б.Ю.

 

Показано, что наиболее часто совершаемые ошибки при использовании непара­мет­ри­ческих критериев согласия типа Колмогорова, типа  и  Мизеса бывают связаны с использованием классических результатов при проверке сложных гипотез или с недооценкой факторов, влияющих на распределения статистик критериев. Показано, как влияют на распределения статистик вид закона, с которым проверяется согласие, тип и число оцененных параметров, конкретное значение параметра, используемый метод оценивания параметров.

 

Введение. В [1] мы отметили ряд ошибок наиболее часто совер­шаемых при использовании критериев согласия типа . Корректному применению этих критериев в приложениях будут способствовать введенные в действие рекомендации по стандартизации Р 50.1.033-2001 [2]. Одновременно с ними Госстандартом РФ были введены в дей­ствие рекомендации по стандартизации Р 50.1.037-2002 [3], регламентирую­щие применение непараметрических критериев согласия типа Кол­мо­го­рова, типа  Мизеса (Крамера-Мизеса-Смирнова) и типа  Мизеса (Ан­дерсона-Дарлинга).

К сожалению, практика применения непараметрических критериев согласия богата не меньшим числом примеров их некорректного ис­пользования, особенно, в литературных источниках учебного характера. Наиболее типичные ошибки связаны с применением классических результа­тов, имеющих силу при проверке простых гипотез, для ситуаций, соот­ветствующих проверке сложных гипотез. Цель этой работы заключается в том, чтобы показать практикам, какие факторы практически влияют на корректность статистических выводов при использовании непараметрических критериев согласия в приложениях и какова степень их возможного влияния на принимаемое решение.

При использовании критериев согласия мы имеем про­стую про­веряе­мую­ гипотезу вида : , если  – известная функ­ция распре­деления веро­ятностей, с которой проверяется согласие на­блюдаемой вы­борки неза­виси­мых одинаково распределенных величин , а  – известное значение параметра (скалярного или вектор­ного). И имеем, например, слож­ную проверяемую гипотезу вида : , если  – функция распре­деления веро­ятностей известного вида, но с неизвестным значением параметра , принадлежащим пространству пара­метров . В процессе про­верки слож­ной гипотезы оценка  параметра вы­числяется по этой же самой вы­борке. Очевидно, что при обработке результатов измерений на прак­тике чаще сталкиваются с проблемой проверки сложных гипотез: сна­чала оценивают по выборки параметры модели, чтобы лучше подогнать ее к наблюдаемым данным, а потом проверяют адекватность модели.

1. Непараметрические критерии при проверке простых гипо­тез. В критерии Колмого­рова в качестве расстояния между эмпириче­ским и теоретическим законом ис­пользуется величина

,

где  – эмпирическая функция распределения,  – теоретиче­ская функция распределения,  – объём выборки. При проверке гипотез обычно ис­пользуется стати­стика вида [4]

,

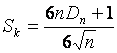где  ,

, ,

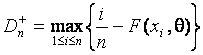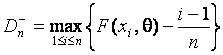 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция закона распределения, согласие с ко­торым про­ве­ряется. Распределение величины  при простой гипотезе в пределе подчиня­ется закону Колмо­горова  [4].

         В критериях типа  расстояние между гипотетическим и эмпи­рическим рас­пределениями рассматривается в квадратичной метрике

,

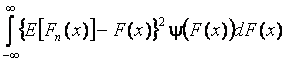где   - оператор математического ожидания.

         При выборе  в критериях типа  Мизеса пользуются стати­с­ти­кой (статистика Крамера-Мизеса-Смирнова) вида

,

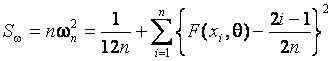которая при простой гипотезе подчиняется распределению  [4].

         При выборе  в критериях типа  Мизеса стати­стика (статистика Андерсона-Дарлинга) имеет вид

.

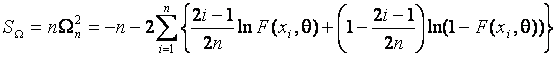В пределе при простых проверяемых гипотезах эта статистика подчиня­ется распределению  [4].

В процессе проверки согласия по выборке вычисляется значение  ста­тистики используемого критерия. Решение о при­нятии или от­клонении гипотезы  делают на основании ус­ловного распре­де­ле­ния  статистики  [для рассматриваемых критериев и про­с­тых гипотез это соответст­венно , , ]. Если вероятность

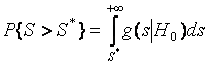
достаточно большая, по крайней мере , где  – ус­ловная плотность, а  – задаваемый уровень значимости (вероятность ошибки пер­вого рода – отклонить справедливую гипотезу ), то при­нято считать, что нет ос­нований для отклонения гипотезы . На прак­тике больше привыкли сравнивать вычисленное значение статистики  с кри­тическим  для заданного значения : гипо­тезу   отвер­гают, если . Критическое значение , опре­деляемое из урав­нения

,

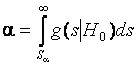обычно берётся из соответ­ствующей статистической таблицы. Подчеркнем, что принятие решения на основании проверки неравенства  является менее предпочтительным, оно менее информативно.

          В случае простых гипотез предельные распределения статистик рассматриваемых не­пара­мет­рических критериев согласия не зави­сят от вида наблюдаемого закона распределения и от его параметров. Го­ворят, что эти критерии являются “свободными от рас­пределения”. Это дос­тоинство предопределило их широкое использование в прило­жениях.

2. Непараметрические критерии при проверке сложных гипо­тез. При проверке сложных гипотез, когда по той же самой выборке оце­нива­ются пара­метры наблюдаемого закона , непарамет­рические критерии согласия теряют свойство “свободы от распределения” [5].

Различия в предельных распределениях тех же самых статистик при про­верке простых и сложных гипотез бывают настолько велики, что прене­брегать этим фактом абсолютно недопустимо. Предостережения о некорректности использования классических результатов при проверке сложных гипотез неодно­кратно поднимались на страницах печати [6-8].

В процессе исследований предельных распределений непарамет­рических критериев согласия при проверке сложных гипотез и к самой процедуре проверки использовался ряд подходов. При достаточно боль­шом объеме выборки ее можно разбить на две части и по од­ной из них оценивать параметры, а по другой проверять согласие [9]. К сожалению, на практике мы чаще имеем дело с выборками достаточно ограниченного объема, поэтому такой подход редко оказывается приемлемым: сущест­венно ухудшается качество оценок параметров и уменьшается мощность кри­териев, т.е. возрастает вероятность ошибок второго рода. В некоторых частных случаях предельные распределения стати­стик исследовались анали­ти­ческими методами [10], процентные точки распределений строились метода­ми статис­тического модели­рования [11-14]. Для при­ближенного вычисления веро­ятностей “согласия” вида  (достигаемого уровня значимости) стро­и­лись фор­мулы, даю­щие достаточно хорошие приближения при малых зна­че­ниях соответ­ст­вую­щих вероятностей [15-19]. Рекомендации [3] построены на результа­тах исследований [20-28] распределений статистик непараметрических критериев согласия и по­строении моделей этих распределений с исполь­зованием мето­дики компьютерного анализа статистических законо­мер­ностей.

При проверке сложных гипотез на условный за­кон рас­пределения статистики  влияет следующий ряд факторов, опреде­ляющих “слож­ность” гипотезы [3]: вид наблюдаемого за­кона , соот­вет­ству­ю­щего истин­ной гипотезе ; тип оцениваемого пара­метра и коли­чество оцениваемых параметров; в некоторых ситуациях конкретное значение параметра (например, в случае гамма-рас­пре­деления); используемый ме­тод оценивания параметров [27]. Это означает, что, проверяя согласие наблюдаемой выборки с законом , в зависимости от комбинации упомянутых факторов мы будем иметь дело с проверкой различных сложных гипотез, каждой из которых соответствует своё (!) предельное распределение одной и той же статистики критерия.

2.1. Характер зависимости от вида закона . На рис. 1 при­ведены распределения статистики критерия согласия типа Колмого­рова при проверке простой гипотезы [распределение Колмогорова ], и сложных гипотез, когда проверяемой гипотезе  соответст­вуют законы нормальный с плотностью 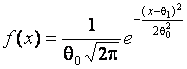, Лапласа 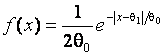, Коши  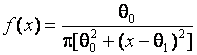и методом макси­маль­ного правдоподобия оцениваются оба параметра закона. Вид соот­ветствующих распределений статистик приведен в рекомендациях [3].

2.2. Характер зависимости от числа оцененных параметров. Влияние количества оцениваемых параметров иллюстрирует рис. 2, на котором представлены распределения статистики типа Колмогорова при проверке сложных гипотез о согласии с законом Su-Джонсона

при вычислении оценок максимального правдоподобия (ОМП) одного, двух, трех или одновременно всех четырех параметров закона. На рисунке отмечены оцениваемые параметры при проверке соответству­ющей сложной гипотезы.

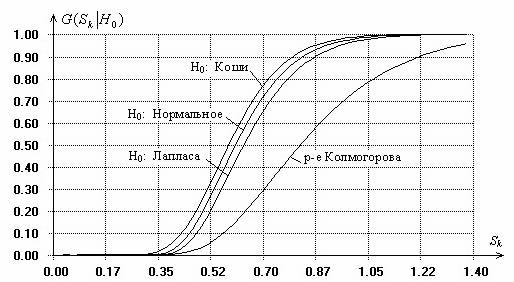
Рис. 1.

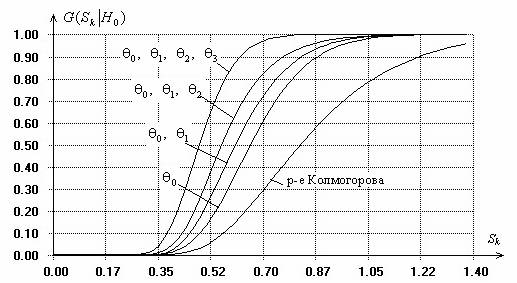
Рис. 2.

 

Насколько велико различие между распределениями статистики при простой и сложных гипотезах? Допустим, при проверке согласия эмпирических данных с распределением Su-Джонсона были вычислены ОМП всех четырех параметров и по­лучено значение статистики Колмо­горова . При проверке простой гипотезы такому значению стати­стики соответствовала бы вероятность  (гипо­тезу надо было бы безоговорочно принять), а при проверке данной слож­ной гипотезы эта же вероятность едва достигает величины  (см. рис. 2). И при уровне значимости  гипо­тезу о согласии следует отклонить.

2.3. Характер зависимости от вида оцененного параметра. Распределения статистик непараметрических критериев согла­сия зависят от вида оцениваемого параметра. Как правило, оценивание пара­метра сдвига в процессе проверки сложной гипотезы приводит к более существенному изменению распределения статистики по сравнению с классическим случаем, соответствующим  проверке простой гипотезы, чем оценивание масштабного параметра или параметра формы закона. Степень зависимости предельных распределения статистик от вида оцениваемого параметра наблюдаемого закона  демонстрируется в [22].

2.4. Характер зависимости от значений параметров законов. В некоторых случаях при проверке сложных гипотез распределения стати­стик непараметрических критериев согласия могут зависеть от конкрет­ного значения параметра. Например, распределения статистик непара­метрических критериев согласия при проверке гипотез относительно гамма-распределения 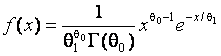 существенно разли­чаются при малых значениях параметра формы , что надо учитывать, и практически пе­рестают меняться при . Модели распределений статистик непара­метрических критериев при проверке сложных гипотез о согласии с гамма-распределениями, соответствующие различным значениям , представлены в [3]. Но гамма-распределение не единственное, из используемых в приложениях, в случае которых рас­пределения статистик критериев зависят от конкретных значений пара­метров. Такую же ситуацию мы имеем при проверке сложных гипотез относительно таких законов и семейств распределений, как распределе­ние Накагами, семейства бета-распределений 1-го и 2-го рода, экспонен­циальное семейство распределений.  Для этих случаев модели распреде­лений статистик рассматриваемых непараметрических критериев согла­сия пока не построены.

2.5. Характер зависимости от метода оценивания параметров. При проверке сложных гипотез распределения статистик непараметриче­ских критериев согласия очень сильно зависят от используемого метода оценивания. На рис. 3 в качестве примера представлены распределения статистики Колмогорова при проверке сложных гипотез о согласии с нормальным законом с оцениванием двух его параметров методом мак­симального правдоподобия и с использованием MD-оценок, получаемых минимизацией самой статистики Колмогорова. Как видим, распределе­ния статистик очень сильно зависят от вида используемых оценок (от метода оценивания). Например, при полученном значении статистики  и задан­ном уровне значимости  в случае использования ОМП гипотезу о нормальном законе следует принять (см. рис. 3), а в случае использова­ния MD-оценок параметров при том же значении статистики и том же уровне значимости – отклонить.

В [3] представлены модели распределений статистик непараметри­ческих критериев согласия и таблицы процентных точек, соответствую­щие двум видам оценок: ОМП и  MD-оценкам. Если используются дру­гие методы оценивания, то нельзя использовать представленные там таб­лицы законов и процентных точек. Например, в случае вычисления оце­нок по методу моментов использование моделей предельных законов, соответствующих применению ОМП, правомерно только тогда, когда оценки по методу моментов совпадают с ОМП. А таких примеров крайне мало.

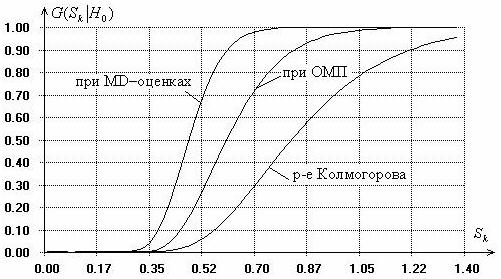
Рис. 3.

 

2.6. Влияние точности оценивания параметров. Как показано выше, метод оценивания параметров (статистические свойства оценок) очень сильно влияют на распределения статистик критериев согласия. Вообще говоря, в редких случаях оценки параметров получаются в виде некоторых статистик (функций от выборок, готовых формул). Чаще оценки находятся в результате реализации определенного итерационного процесса и найденные значения представляют собой некоторые приближения искомого реше­ния.

Как влияет точность вычисления оценок на распределение ста­тистики применяемого критерия согласия? Если асимптотические свой­ства приближенных оценок совпадают с асимптотическими свойствами точных оценок, то распределения статистик непараметрических крите­риев согласия при использовании и тех, и других оценок совпадают. На­пример, на практике достаточно часто используют так называемые од­ношаговые оценки [29], которые формируются как первые приближения ОМП, вычисляемые в результате одной итерации метода Ньютона. Пока­зано, что такие оценки асимптотически эффективны и, следовательно, их асимптотические свойства совпадают со свойствами ОМП. В случае применения одношаговых оценок можно пользоваться в качестве пре­дельных распределений статистик законами, построенными для ОМП [30]. То есть, в то время как метод оценивания значимо влияет на законы распределения статистик критериев, точность вычисления оценок на распределениях тех же статистик или не отражается, или отражается в существенно меньшей степени.

2.7. Влияние объема выборок на распределения статистик. В большинстве источников, касающихся применения непараметрических критериев согласия (при проверке простых гипотез), как правило, упо­минается, что предельными распределениями , ,  для со­ответствующих критериев можно пользоваться, начиная с объемов вы­борок  наблюдений. Вообще говоря, и при проверке про­стых, и при проверке сложных гипотез распределения статистик рас­сматриваемых критериев  достаточно близки к предельным (не очень сильно отличаются) уже при объемах выборок  наблюде­ний [22]. Проблемы в другом.

При малых  бывает очень трудно различить пару близких конкури­рующих гипотез  и , так как очень близкими оказываются распределения  и . Любой практик может заметить, что при малых  с равным успехом могут быть приняты гипотезы о согласии с целым рядом существенно отличающихся моделей законов. Способ­ность любых статистических критериев различать гипо­те­зы, то есть их мощность, возрастает с ростом объема выборок. В случае проверки простых гипотез различить два близких закона распределения, опираясь на непараметрические критерии согласия, очень проблема­тично. Это можно сделать достаточно надежно лишь при больших объе­мах выборок [31]. На рис. 4 приведены распределения стати­стики Колмо­го­рова при справедливости простой проверяемой гипотезы = и при справедливости конкурирующей гипотезы  при объемах выборок 100, 300, 500, 1000 и 2000 наблюде­ний. Проверяемой гипотезе  соответствует нормальный закон, конкури­рующей гипотезе  – логистический с функцией плотности

.

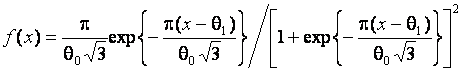Эти два закона очень близки и, как правило, трудно различимы с помо­щью критериев согласия. По рисунку видно, что при заданной вероятно­сти ошибки 1-го рода (уровне значимости)  мощность критерия , где  – вероятность ошибки 2-го рода, составляет величины по­рядка 0.114 (всего!) при 100, 0.14 при 300, 0.16 при 500, 0.235 при 1000 и 0.38 при 2000.

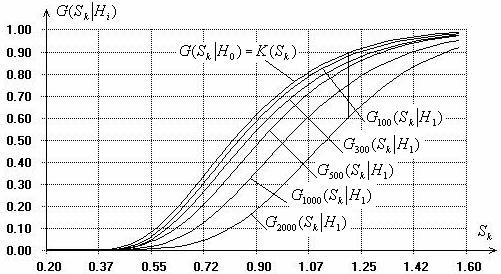
Рис. 4.

На рис. 5 отражена аналогичная картина при проверке сложной ги­потезы о согласии с нормальным законом с оцениванием параметров нормального закона методом максимального правдоподобия при той же конкурирующей гипотезе  по критерию типа Колмогорова. На ри­сунке представлены функция распределения  и функции  при объемах выборок 20, 50, 100, 300, 500, 1000 и 2000 на­блюдений. При том же уровне значимости  мощ­ность критерия оказывается существенно выше (в 2, 3 и более раз) и составляет величины порядка 0.134 при 20, 0.17 при 50, 0.23 при 100, 0.34 при 200, 0.45 при 300, 0.64 при 500, 0.91 при 1000 и 0.995 при 2000. Это свидетельствует о том, что в случае проверки сложных гипо­тез те же близкие гипотезы могут различаться при средних объемах выборок.

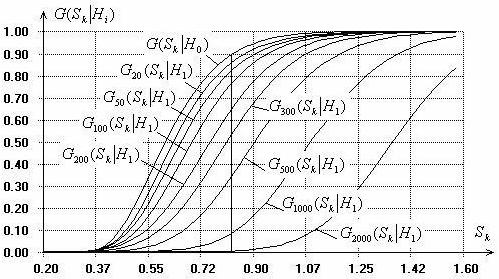
Рис. 5.

 

Излагая особенности применения критериев согласия при проверке сложных гипотез, мы иллюстрировали их свойства на примере критерия типа Колмогорова. Аналогичная картина характерна для пове­дения распределений статистик других непараметрических критериев [3].

Заключение. Боль­шинство ошибок применения непараметричес­ких критериев согласия, приводящих к не­корректным выводам, бывает связано с полным пренебрежением того, что, оценивая по выборке параметры, оказываются в условиях проверки сложной гипотезы.

В тех редких случаях, когда исследователь бывает в курсе, что нельзя пользоваться классическими результатами, осуществляя проверку сложной гипотезы, ошибки бывают связаны с тем, что не учитывается многообразие факторов, влияющих на распределение статистики крите­рия согласия. Обычно не учитывается, что распределения статистик за­висят от метода оценивания.

При выборе методов анализа следует учитывать точность регист­рации наблюдений, иначе это может приводить к недоразумениям при статистических выводах. При анализе экспериментальных наблюдений мы чаще имеем дело с недостаточными объемами выборок. Однако в не­которых случаях, например, при автоматизированном контроле различ­ных показателей выборки могут быть практически любого объема. Но при этом измерения снимаются с ограниченной точностью. В результате в накапливаемой выборке наблюдения принимают ограниченное число значений: выборка оказывается поразрядно группированной, а соответ­ствующее эмпирическое распределение  сохраняет ступенчатый вид при любом объеме выборки. Вследствие этого, меры отклонения  от , используемые в непараметрических критериях согла­сия, не смотря на возможное соответствие наблюдаемого закона теоре­тическому, с ростом объема выборок только растут. В такой ситуации проверка гипотезы о принадлежности контролируемой величины, например, нор­мальному закону неизбежно приводит к отклонению проверяемой гипо­тезы. И это притом, что к контролируемому процессу претензий может не быть. Точность регистрации наблюдений следует учитывать и при вы­боре метода оценивания параметров, и при выборе критерия проверки гипотез. В подобной ситуации целесообразней воспользоваться крите­риями типа .

Таким образом, применяя непараметрические крите­рии согласия типа Колмогорова, типа 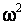 и 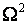 Мизеса, следует очень вни­мательно относиться к тому, какую гипотезу Вы проверяете: простую или сложную. Если сложную, то следует внимательно учесть факторы, влияющие на “сложность” гипотезы (вид закона 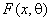, метод оценива­ния, тип оцениваемых параметров, их количество, значение оценки па­раметра), и использовать при проверке гипотезы соответ­ствующее рас­пределение [3] статистики применяемого критерия.

 Рекомендации по стандартизации [3] охватывают далеко не полный перечень законов распределения, применяемых в приложениях. В конкретных задачах, в конкретных приложениях для описания наблюдаемых случайных величин могут использоваться специфические модели законов рас­пределений. Естественно, что возникает необхо­ди­мость проверки адекватности таких моделей. Для проверки адекватности с исполь­зованием критериев согласия необходимо знание условных распределений статистик . Очень проблематично, чтобы необ­ходимые  были найдены анали­тиче­ски (из-за сложности реше­ния таких задач аналитическими методами и множества таких задач). Но построение моделей  с использованием компьютерных методов исследования [32] принци­пиаль­ных проблем не вызывает. На базе таких методов были построены рас­пределения статистик и таблицы про­центных точек, представленные в рекомендациях [3].

 

ЛИТЕРАТУРА

1.     Лемешко Б.Ю., Чимитова Е.В. // Измери­тельная техника. 2002. - № 6. - С. 5-11.

2.     Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть I. Критерии типа хи-квадрат. - М.: Изд-во стандартов. 2002. - 87 с.

3.     Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть II. Непараметрические критерии. - М.: Изд-во стандар­тов. 2002. - 64 с.

4.     Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

5.     Kac M., Kiefer J., Wolfowitz J. // Ann. Math. Stat. – 1955. – V.26. – P.189-211.

6.     Орлов А.И. // Заводская лаборатория. – 1985. – Т. 51. – №1. – С. 60-62.

7.     Бондарев Б.В. // Заво­дская лаборатория. – 1986. – Т. 52. – № 10. – С. 62-63.

8.     Кулинская Е.В., Саввушкина Н.Е. // За­водская лаборатория. – 1990. – Т. 56. – № 5. – С. 96-99.

9.     Durbin J.  // Lect. Notes Math. – 1976. – V. 566. – P. 33–44.

10. Мартынов Г.В. Критерии омега–квадрат. – М.: Наука, 1978. – 80 с.

11. Pearson E.S., Hartley H.O. Biometrica tables for Statistics. V.2. – Cam­bridge: University Press, 1972. – 634 p.

12. Stephens M.A. // J. R. Stat. Soc. – 1970. – B. 32. – P. 115-122.

13. Stephens M.A. // J. Am. Statist. Assoc. – 1974. – V.69. – P. 730-737.

14. Chandra M., Singpurwalla N.D., Stephens M.A. // J. Am. Statist. Assoc. ­– 1981. – V.76. – P. 375.

15. Тюрин Ю.Н. // Изв. АН СССР. Сер. Матем. – 1984. – Т. 48. – № 6. – C. 1314-1343.

16. Тюрин Ю.Н., Саввушкина Н.Е. // Изв. АН СССР. Сер. Техн. Кибернетика. – 1984. – № 3. – C. 109-112.

17. Тюрин Ю.Н. Исследования по непараметрической статистике (непа­ра­мет­рические методы и линейная модель): Автореф. дисс. … д–ра физ.–мат. наук. – М., 1985. – 33 с. – (МГУ).

18. Саввушкина Н.Е. // Сб. тр. ВНИИ систем. исслед. – 1990, № 8. – С.50-56.

19. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. – М.: ИНФРА–М, Финансы и статистика, 1995. – 384 с.

20. Лемешко Б.Ю., Постовалов С.Н. // Надежность и кон­троль качества. – 1997. – № 11. – С. 3-17.

21. Лемешко Б.Ю., Постовалов С.Н. // Тр. IV международной конференции “Актуальные проблемы элек­трон­ного приборо­строения”. – Новосибирск. – 1998. – Т. 3. – С. 12-16.

22. Лемешко Б.Ю., Постовалов С.Н. // Заво­дская лаборатория. – 1998. – Т. 64. – № 3. – С. 61-72.

23. Лемешко Б.Ю., Постовалов С.Н. Прикладная статис­тика. Правила про­верки согласия опытного распределения с тео­ретическим. Мето­дические реко­мендации. Часть II. Непа­раметрические критерии. – Но­восибирск: Изд-во НГТУ. – 1999. – 86 с.

24. Lemeshko B.Yu., Postovalov S.N. // Proceedings The Third Russian-Korean International Symposium on Science and Technology (KORUS-99). Novosibirsk. Russia. June 22-25, 1999. Vol.2. - P.501-504.

25. Лемешко Б.Ю., Постовалов С.Н. // Методы менеджмента каче­ства. Надежность и контроль качества. - 1999. № 11. - C. 34-43.

26. Лемешко Б.Ю., Постовалов С.Н. // Автометрия. 2001. - № 2. - С. 88-102.

27.  Лемешко Б.Ю., Постовалов С.Н. // Заводская лаборатория. Диагностика материалов. 2001. Т. 67. - № 7. - С. 62-71.

28. Лемешко Б.Ю., Постовалов С.Н. // Доклады СО АН ВШ. 2002. - № 1(5). - С.65-74.

29. Орлов А.И. // Заводская лаборатория. 1986. – Т. 52. – № 5. – С. 67-69.

30. Лемешко Б.Ю., Чимитова Е.В. // Заводская лаборатория. Диагностика материалов. 2003. Т. 69. – № 5. – С.62-68.

31. Орлов А.И. // Заводская лаборатория. 1991. Т. 57. № 7. – С. 64-66.

32. Лемешко Б.Ю. // Сб. "Моделирование, автоматизация и оптимизация наукоемких технологий". - Новосибирск: изд-во НГТУ, 2000. - С. 18-19.


[1] Работа выполнена при  финансовой поддержке Минобразования России (проект № Т02-3.3-3356)