См. также: Прикладная математическая статистика (материалы к семинарам)

 

Метрология. 2004. № 7. – С. 8-17

519.25

 

О задаче идентификации закона распределения случайной составляющей погрешности измерений[1]

 

ЛЕМЕШКО Б.Ю.

 

Сравниваются подходы к задаче идентификации закона распределения. Показывается предпочтительность подхода, базирующегося на аппа­рате математической статистики. Отмечаются недостатки при решении задач идентификации на практике.

Ключевые слова: закон распределения, оценка параметров, критерии согласия, проверка сложных гипотез.

The approaches to the distribution law identification have been compared. The approach based on mathematical statistics methods has been shown to be preferable. Failings in solving the identification problem in practice have been pointed out.

Key words: distribution laws, estimation of parameters, goodness-of-fit tests, composite hypothesis testing.

 

Введение. Под задачей идентификации закона распределения на­блюдаемой случайной величины (структурно-параметрической иденти­фикации), как правило, понимают задачу выбора такой параметрической модели закона распределения вероятностей, ко­торая наилучшим образом соответствует результатам эксперименталь­ных наблюдений. Случайные ошибки средств измерений не так уж часто подчиняются нормальному закону [1], точнее, не так часто хорошо описываются моделью нормаль­ного закона. В основе измерительных приборов и систем лежат различ­ные физические принципы, различные методы измерений и различные преобразования измерительных сигналов. Погрешности измерений как вели­чины являются следствием влия­ния множества факторов, случайного и неслучайного характера, дейст­вующих постоянно или эпизодически. По­этому понятно, что только при выполнении определенных предпосылок (теоретических и технических) погрешности измерений достаточно хорошо описываются моделью нормаль­ного закона.

Вообще говоря, следует понимать, что истинный закон распреде­ления (если он, конечно, существует), описывающий погрешности конкретной измерительной системы, оста­ется (останется) неизвестным, не смотря на все наши попытки его иден­тифицировать. На основании данных измерений и тео­ретических соображений мы можем только подобрать вероятностную модель, которая в некотором смысле наилучшим образом приближает этот истинный закон. Если построенная модель адекватна, то есть применяемые критерии не дают оснований для ее отклонения, то на основе данной модели можно вычис­лить все инте­ресующие нас вероятностные характеристики случайной составляющей погрешности измеритель­ного средства, которые будут отличаться от истинных значений только за счет неисключенной систематической (ненаблюдаемой или нерегистрируемой) составляющей погрешности измерений. Ее малость и характеризует правильность измерений.

Множество возможных законов распределения вероятностей, ко­торые можно использовать для описания наблюдаемых случайных вели­чин, неограничено. Бессмысленно ставить целью задачи иден­тификации нахождение истинного закона распределения наблюдаемой величины. Мы можем лишь решать задачу выбора наилучшей модели из некоторого множества. Например, из того множества параметрических законов и се­мейств распределений, которые используются в приложе­ниях, и упоми­нание о которых можно найти в литературных источниках.

Классический подход к структурно-параметрической иден­ти­фикации закона распределения. Под классическим подходом будем понимать алгоритм выбора закона распределения, целиком бази­ру­ю­щийся на аппарате математической ста­тистики. Такой подход к иденти­фикации закона распределения заключа­ется в последовательной реали­зации следующей двухэтапной процедуры для каждого вида параметри­ческой модели из рассматриваемого множе­ства законов. На первом этапе процедуры на основании выборочных данных строится модель закона определенного вида (из рассмат­рива­емого мно­жества моделей), оцени­ваются параметры этой модели. На вто­ром этапе оценивается степень адекватности полученной модели экспе­рименталь­ным наблюдениям, как правило, с применением различных критериев согласия.

Эти два этапа для -й модели из множества моделей размерности  можно записать как задачу проверки сложной гипотезы с исполь­зова­нием критерия согласия

 : ,                              (1)

где  – функция распре­деления веро­ятностей известного вида, но с неизвестным значением параметра , принадлежащим пространству пара­метров , . Подчеркнем, что в ходе про­верки слож­ной гипо­тезы оценка параметра  вы­числяется по этой же самой вы­борке. В про­цессе проверки гипотезы  по выборке вычисляется значение  ста­ти­стики используемого критерия согласия. На основании ус­ловного рас­пре­де­ле­ния  статистики  критерия вычисляется вероятность (достигнутый уровень значимости)

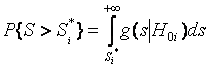,                                  (2)

где  – ус­ловная плотность распределения статистики критерия при справедливости гипотезы .

В процессе идентификации выбирается та модель  закона распределения, на предпочтительность которой в вероятностном смысле (по достигаемому уровню значимости ) указывает исполь­зуе­мый статистический критерий:

,                 (3)

где  – задаваемый уровень значимости (вероятность ошибки пер­вого рода – отклонить справедливую гипотезу ).

Успех данного подхода зависит от двух условий: полноты рас­смат­риваемого множества моделей и корректности применения соответству­ющих статистических методов. Последнее касается как используемых мето­дов оценивания параметров, так и критериев проверки статис­ти­че­ских гипотез. При проверке сложных гипотез вида (1) обязательно сле­дует учитывать, что на распределения статистик кри­териев согласия влияют используемые методы оценивания пара­метров. О типичных ошибках применения критериев типа  подробно гово­рит­ся в [2], а об ошибках применения непараметрических критериев – в [3].

Достаточно предста­ви­тельное множество моделей для решения конкретной задачи идентификации в настоящее время можно рас­сматри­вать только с использованием соответствующего программного обеспе­чения. В этом случае предпочтительнее программные системы, обеспе­чивающие выбор из большего числа видов законов распределений [4, 5] и позволяющие компоновать модели законов распределений в виде сме­сей законов (двух и более) из имеющегося множества моделей [6-9].

Классический подход к задаче идентификации, на наш взгляд, яв­ляется наиболее предпочтительным, хотя бы в связи с тем, что получен­ные по выборкам значения статистик используемых критериев согласия определяют соответствующие расстояния между эмпирическим и теоре­тическим законом распределения.

Так как в критериях согласия типа  [10], в непараметрических кри­териях типа Колмогорова, типа  Крамера-Мизеса-Смирнова, типа  Андерсона-Дарлинга [11] ис­поль­зуются различные меры, то крите­рии по-разному улавливают в выборках различные отклонения от пред­полагаемых теоретических законов. В этой связи проверку гипотез (1) и идентификацию закона целесообразно проводить с использованием ряда критериев согласия. В этом случае окончательное решение может быть при­нято либо по сово­купности критериев, когда выбирается модель , для которой достигаемый уровень значимости по всем крите­риям максимален

,             (4)

где  – число используемых критериев согласия, либо по некоторому компромиссному, взвешенному критерию.

Предпочтительность данного подхода можно связать и с появ­ле­нием рекомендаций по стандартизации [10, 11]. Благодаря реко­мен­да­циям [10] стала возможной проверка сложных гипотез вида (1) с исполь­зованием непараметрических критериев согласия при доста­точ­но пред­ставительном множестве законов распределений, а приводимые в реко­мендациях [11] таблицы асимптотически оптимального группи­ро­вания повышают идентификационные возможности критериев типа  (вслед­ст­вие большей мощности критериев по отношению к близким аль­терна­тивам).

Успех в выборе модели закона, наилуч­шим образом описываю­щего наблюдаемую случайную величину,  не в последнюю очередь зави­сит от применяемых методов оценивания. Желательно, чтобы ис­пользу­емые методы давали оценки параметров, обладающие лучшими стати­стическими свойствами (несмещенные, состоятельные и эффективные или асимп­тотически эффективные оценки). Желательно, чтобы оценки были робастными, то есть устойчивыми к малым отклонениям от пред­положений, к выбросам. Однако хорошие статистические свойства оце­нок не всегда сопровождаются свойствами робастности.

При учете введенной Рао [12] эффективности второго порядка наи­лучшими статистическими свойствами обладают оценки макси­мального правдоподобия (ОМП), получаемые в результате максимизации по  функции  правдоподобия

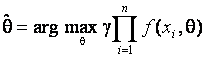,                                            (5)

где  – некоторая константа, и  – функция плотности, зависящая от параметра ,  – объем выборки,  – выборочные наблюдения. Однако ОМП по точечным (негруппированным) выборкам, за редким исключением, не являются робастными [13]. Поэтому имеющиеся в реальных выборках выбросы и другие отклонения от предполагаемого закона могут испортить всю картину.

Следовательно, используя ОМП, необходимо быть уверенным в отсутствии в выборке аномальных измерений или исключить их в процессе обработки. Для этого могут применяться робастные методы оценивания и параметрические алгоритмы отбраковки, опирающиеся на эти методы [14]. Высокой устойчивостью к наличию в выборках аномальных наблюдений обладают ОМП по группированным данным [13] и оптимальные L-оценки по выборочным квантилям [15, 16].  Хорошие робастные свойства [17] у MD-оценок [18], определяемых соотношением

,                              (6)

где  – эмпирическая функция распределения,  – расстояние в пространстве функций распределения для функций  и .  Любая статистика, из используемых в критериях согласия, может быть положена в основу этого метода оценивания.

Признаком наличия в анализируемой выборке выбросов (данных или результатов измерений, ано­мальных с позиций рассматриваемого закона ) может яв­ляться су­щественное отличие в значениях ОМП и некоторой робаст­ной оценки, например, ОМП по сгруппированным данным. В этом случае, опираясь на робастную оценку параметра , следует восполь­зо­ваться пара­метрическим алгоритмом отбраковки [14], исключив выбросы, а затем снова вычислить ОМП.

Топологические методы идентификации. Существует ряд под­ходов, упоминаемых в [19], общим для которых является попытка иден­тифицировать вид закона распределения на основании значений оценок некоторых числовых характеристик, вычисляемых по выбо­роч­ным дан­ным. Например, по значениям оценок коэффициентов асиммет­рии 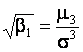 и эксцесса 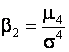, где  – центральный мо­мент случайной величины порядка , . Подставив в выражения для коэффициентов асиммет­рии и эксцесса оценки соответствующих моментов, получим точку в плоскости (,), положение которой укажет нам наиболее предпочтительный закон распределения. В [1] решение предлагается принимать по значениям оценок контрэксцесса  и энтропийного коэффициента , где 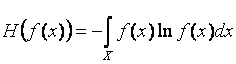 – дифференциаль­ная эн­тропия величины . В этом случае получают точку в плоскости (,), которая должна указать подходящий закон.

Идеи привлекательны: получив точку в соответствующей плоско­сти, можно сразу указать вид закона (определить структуру модели). Од­нако работоспособность такого подхода на практике не выдерживает критики из-за плохой устойчивости оценок центральных моментов высо­ких порядков. Выборочные оценки таких моментов не являются робаст­ными. Они очень чувствительны к незначительным отклонениям выбо­рочных данных от предполагаемого закона, к наличию выбросов. Предла­гаемая в [1] оценка энтропийного ко­эффициента

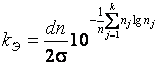,                                       (7)

где – длина интервала,  – объем выборки,  – число наблюдений в -м интервале,  – число интервалов в построенной по выборке гисто­грамме с равной длиной всех интервалов, чувствительна не только к вы­бросам и отклонениям от предполагаемого закона, но и к произвольно выбираемой длине интервала.

В топологических методах при объемах выборок, типичных для задач метрологии, степень неопределенности при идентификации закона оказывается очень высокой. Действенность подхода можно проде­мон­ст­рировать только на идеализированных модельных данных.

Сравнительный анализ подходов. Безусловно, классический подход базируется на более основательном математическом аппарате, включающем методы статистического анализа, учитывающие специфику решаемых задач и вид законов, входящих в рассматриваемое множество моделей. При таком подходе и корректном использовании методов ста­тистического анализа выводы о наиболее подходящем законе распреде­ления всегда будут более обоснованы, чем при топологическом.

Топологический подход можно рекомендовать лишь как способ, позволяющий в первом приближении очертить некоторую группу моде­лей законов распределения, пригодную для описания наблюдаемой слу­чайной величины.

Если при идентификации оперировать терминами ошибок первого и второго рода, мощностью критериев проверки гипотез, то, конечно, в случае классического подхода мы имеем дело с более мощными крите­риями. Однако нельзя утверждать, что в любом случае процедура иден­тификации (1)-(4) является наилучшей.

Хотя критерии согласия при про­верке сложных гипотез (1), как правило, мощнее, чем при проверке про­стых, они не являются наиболее мощными критериями, ориентирован­ными на проверку гипотез о согла­сии с конкретным законом.  То есть,  для проверки гипотез вида (1) для конкретного закона  можно по­строить критерий, ориен­тирован­ный на этот закон, более мощный, чем критерий согласия. Например, как показали наши исследования, крите­рии нормальности Шапиро-Уилка и Эппса-Палли [20] при объемах вы­борок от 10 до 100 мощнее (относи­тельно близких альтернатив) непара­метрических кри­териев согласия и критериев типа , используемых для проверки гипотез о согласии с нор­мальным законом.

Примечание: Следует отметить, что критерии нормальности Шапиро-Уилка и Эппса-Палли имеют и недостатки: при малых объемах выборок они не спо­собны отличать от нормального закона распределения экспонен­ци­аль­ного семейства, более плосковершинные по сравнению с нор­маль­ным законом. Наши исследования показали, что из-за повышенных вероят­ностей ошибок первого рода нецелесо­образно применение включен­ного в стандарт [20] модифици­рован­ного критерия Шапиро-Уилка. Кроме того, в данный стандарт оказался не включенным наиболее мощный из известных критерий нормальности.

Состояние исследований. Остановимся на некоторых недостатках в подходе к задаче идентификации законов распределений, которые, на наш взгляд, прослеживаются в работах, связанных с вероятностным опи­санием погрешностей измерений.

Первое, что, по-видимому, следует отметить, это “историческая” ограниченность множества моделей, используемых для описания за­ко­нов распределения ошибок измерений, и искусственность многих приме­няемых моделей (треугольное, трапецеидальное и т.п. распределения) [1, 21]. В реальных задачах неоправданно редко в качестве моделей исполь­зуется экспоненциальное семейство распределений с плотностью

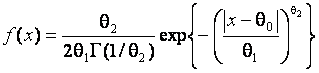,                         (7)

редко рассматривают модели в виде смесей законов.

Во-вторых, определенная тяга к формализации процесса иден­ти­фикации законов распределения [1, 19, 22], причем в некотором отрыве от современного аппарата математической статистики. Примеры попы­ток такой формализации можно назвать, скорее, намерениями, а не ре­альными попытками.

В-третьих, можно отметить недостаточную нацеленность при ре­шении задач идентификации на использование развитого про­грам­много обеспечения задач статистического анализа или на его разработку. Прак­тически не используются при исследовании вероятностных закономер­ностей возможности компьютерного моделирования, а если использу­ются, то ошибки применения аппарата математической статистики при моделировании сводят на нет результаты исследований.

Например, ряд ошибок, связанных с вопросами применения крите­риев согласия, содержится в работе [21], где делается попытка сравни­тельного исследования ряда рассматриваемых критериев согласия при ограниченных объемах выборок. В частности, исследуется способность критериев отличить друг от друга четыре закона: нормальный, треуголь­ный, трапецеидальный и равномерный. Отметим, что это существенно отличающиеся законы распределения и при больших объемах выборок нет проблемы их распознавания. Вполне естественно в целях исследова­ния свойств критериев применение статистического моделирования, хотя не в таком урезанном виде, как в [21]. Принципиальная ошибка всего ис­следования, проведенного в [21],  заключается в том, что выбор в пользу одной из четырех рассматриваемых гипотез осуществлялся по значениям статистики соответствующего критерия. Это было бы справедливо, если бы проверялись простые гипотезы. Но в данном случае речь шла о про­верке сложных гипотез: параметры законов оценивались по тем же са­мым смоделированным выборкам. В такой ситуации распределения ста­тистик всех рассматриваемых непараметрических критериев согласия за­висят от вида закона, с которым проверяется согласие, от того, какие па­раметры оцениваются, и от метода оценивания параметров [10]. Это оз­начает, что при одном и том же уровне значимости критические области одного и того же критерия при проверке согласия эмпирического рас­пределения с различными теоретическими законами не совпадают. И не совпадают очень существенно. Поэтому результаты моделирования, представлен­ные в [21], являются некорректными.

Необходимо также отметить, что статистики, названные в [21, стр. 6] статистиками критериев Мизеса и Пирсона “сложного”, в том виде, как они приведены в [21], вообще не являются статистиками критериев согласия, так как в них не задается расстояния между теоретическим и эмпирическим распределениями.

Еще одно недоразумение в [21] связано с предложенной “моди­фи­кацией” критерия . В результате такой модификации статистика изме­ряет расстояние не между эмпирическим и теоретическим законом, соот­ветствующим проверяемой нулевой гипотезе, а между построенной ядерной оценкой плотности и теоретическим законом с параметрами, оцененными по данной выборке. То есть, измеряется расстояние между двумя различными оценками закона распределения. В этом случае малое значение статистики критерия будет говорить о близости оценок друг другу, а не о близости их эмпирическому закону распределения. Но именно в проверке такой близости заключается цель применения крите­рия согласия.

Заключение.

Решение задач структурно-параметрической идентификации при ограниченных объемах выбо­рок, которыми, как правило, обладают мет­рологи, обостряет проблему. В этом случае еще более важными оказы­ваются корректность применения статистических методов анализа, ис­пользование оценок, обладающих наилучшими статистическими свойст­вами, и критериев, обладающих наибольшей мощностью.

При решении задач идентификации предпочтительнее опираться на классический подход. При идентификации рекомендуется рассматри­вать более широкое множество законов распределения, в том числе мо­дели в виде смесей законов. В этом случае для любого эмпирического распределения мы всегда сможем построить адекватную, статистически существенно более обоснованную математическую модель.

Следует ориентироваться на использование и разработку про­грам­мных систем, обеспечивающих решение задач структурно-параметри­че­ской идентификации зако­нов распределений при любой форме ре­гистри­руемых наблюдений (измерений), включающих современные методы статис­тического анализа, ориентиро­ваться на широкое, но корректное исполь­зование в исследованиях методов компьютер­ного моделирования.

 

ЛИТЕРАТУРА

1.     Новицкий П.В., Зограф И.А. Оценка погрешностей результатов из­ме­рений. – Л.: Энергоатомиздат, 1991. – 303 с.

2.     Лемешко Б.Ю., Чимитова Е.В. Об ошибках и неверных действиях, со­вершаемых при использовании критериев согласия типа // Измери­тельная техника. 2002. – № 6. – С. 5-11.

3.     Лемешко Б.Ю. Об ошибках, совершаемых при использовании непараметрических критериев согласия // Измерительная техника. 2004. – №2. – С. 15-20.

4.     Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. – Новосибирск: Изд-во НГТУ, 1995. – 125 с.

5.     Лабутин С.А., Пугин М.В. Статистические модели и методы в измери­тельных задачах. – Н. Новгород: НГТУ, 2000. – 115 с.

6.     Лемешко Б.Ю., Постовалов С.Н. Статистический анализ смесей распределений по частично группированным данным // Сб. научных трудов НГТУ. – Новосибирск: Изд-во НГТУ, 1995. – № 1. – С. 25-31.

7.     Лемешко Б.Ю., Постовалов С.Н. Программное обеспечение статистического анализа смесей случайных величин, представленных частично группированными и интервальными выборками // Тр. третьей МНТК "Актуальные проблемы электронного приборо­стро­ения АПЭП-96". – Новосибирск, 1996. – Т. 6. – Ч.1. – С.50-53.

8.     Лемешко Б.Ю., Постовалов С.Н. Система статистического анализа наблюдений и исследования статистических закономерностей // Сб. "Моделирование, автоматизация и оптимизация наукоемких технологий". – Новосибирск: изд-во НГТУ, 2000. – С. 44-46.

9.     Лабутин С.А., Алешкин А.Н. Аппроксимация двухмодальных распреде­лений случайных величин // Измери­тельная техника. 2002. – № 3. – С. 10-14.

10. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть II. Непараметрические критерии. – М.: Изд-во стандар­тов. 2002. – 64 с.

11. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная стати­стика. Правила проверки согласия опытного распределения с теорети­ческим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.

12. Rao C.R. Criteria of estimation in large samples // Sankhua, 1962. – V. 25. – P. 189-206.

13. Лемешко Б.Ю. Группирование наблюдений как способ получения робастных оценок // Надежность и контроль качества. – 1997. –  № 5. – С. 26-35.

14. Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномаль­ных измерений // Заводская лаборатория. – 1997. – Т.63. – № 5. – С. 43-49.

15. Лемешко Б.Ю., Чимитова Е.В. Построение оптимальных L-оценок па­раметров сдвига и масштаба распределений по выборочным кванти­лям // Сибирский журнал индустриальной математики. 2001. – Т.4. – № 2. – С. 166-183.

16. Лемешко Б.Ю., Чимитова Е.В. Оптимальные L-оценки параметров сдвига и масштаба распределений по выборочным квантилям // Заво­дская лаборатория. Диагностика материалов. 2004. – Т.70. – №1. – С. 54-66.

17. Шуленин В.П. Введение в робастную статистику. – Томск: Изд-во Том. ун-та, 1993. – 227 с.

18. Wolfowitz J. The minimum distance method // Ann. Math. Stat., 1957. V. 28. – P. 75-88.

19. Яшин А.В., Лотонов М.А. Выбор метода решения задачи идентифика­ции законов распределения случайных погрешностей средств измере­ний // Измери­тельная техника. 2003. – № 3. – С. 3-5.

20. ГОСТ Р ИСО 5479-2002. Статистические методы. Проверка отклоне­ния распределения вероятностей от нормального распределения. – М.: Изд-во стандартов. 2002. – 30 с.

21. Яшин А.В., Храпов Ф.И. Выбор критерия согласия для определения за­кона распределения измеряемой величины // Измери­тельная тех­ника. 2002. – № 1. – С. 16-20.

22. Яшин А.В. Определение закона распределения случайных погрешно­стей вторичных эталонов // Измери­тельная техника. 2003. – № 1. – С. 10-12.


[1] Работа выполнена при  финансовой поддержке Минобразования России (проект № Т02-3.3-3356)