Метрология. 2005. № 2. С.3-23
УДК 519.233.3: 006.91.001
Сравнительный анализ критериев проверки отклонения распределения
от нормального закона
Б.Ю. Лемешко, С.Б. Лемешко
Исследованы распределения статистик и мощность ряда критериев проверки отклонения от нормального закона, в том числе, не вошедших в ГОСТ Р ИСО 5479-2002. Показаны достоинства и недостатки различных критериев.
См. далее:
Лемешко Б.Ю., Рогожников А.П. Исследование особенностей и мощности некоторых критериев нормальности // Метрология. 2009. № 4. – С. 3-24.
Лемешко Б.Ю., Рогожников А.П. О
нормальности погрешностей измерений в классических экспериментах и мощности
критериев, применяемых для проверки отклонения от нормального закона //
Метрология. 2012. № 5. – С. 3-26.
См. также: Прикладная математическая статистика (материалы к семинарам)
Введение. Принадлежность наблюдаемых данных нормальному закону является необходимой предпосылкой для корректного применения большинства классических методов математической статистики, используемых в задачах обработки измерений, стандартизации и контроля качества. Поэтому проверка на отклонение от нормального закона является частой процедурой в ходе проведения измерений, контроля и испытаний.
Отечественный стандарт ГОСТ Р ИСО 5479-2002 “Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения” [1], введенный в действие в 2002 г., представляет собой аутентичный текст международного стандарта ISO 5479-97. В стандарте рассматривается графический метод проверки на нормальность с использованием вероятностной бумаги, критерии проверки на симметричность и на значение эксцесса, статистики которых представляют собой функции от оценок моментов закона распределения, критерии Шапиро-Уилка, основанные на регрессионном анализе порядковых статистик, критерий Эппса-Палли, статистика которого измеряет некоторое расстояние между выборочной характеристической функцией и характеристической функцией нормального закона.
На наш взгляд, введенный стандарт [1] не позволяет его пользователям ориентироваться в том, какой из критериев является предпочтительней, какой из них оказывается наиболее мощным, против каких альтернатив и при каких объемах выборок конкретный критерий обладает преимуществом или наоборот.
В стандарте отказываются от использования критериев
типа 
и не упоминается применение для проверки нормальности
непараметрических критериев согласия.
В отечественной литературе можно найти много примеров, связанных с проверкой отклонений от нормального закона, но исследованию специальных критериев, предназначенных для этих целей, уделено достаточно мало внимания [2, 3]. Напротив, в зарубежных источниках исследованию критериев проверки отклонений от нормальности посвящено значительное число работ. Уделено внимание и анализу мощности критериев при проверке отклонений от нормального закона по отношению к различным альтернативам [4, 5]. Подчеркивается, что критерии согласия при малых объемах выборок проигрывают по мощности специальным критериям проверки на отклонение от нормальности [4] и предпочтение, как правило, отдается критерию Шапиро-Уилка. В то же время не складывается полной картины того, когда и каким критерием целесообразней пользоваться при проверке отклонений распределения от нормального.
В свете вышесказанного для заинтересованных специалистов остается неясным, насколько обоснован выбор критериев в стандарте, каковы их достоинства и недостатки, какова их мощность, как меняются распределения статистик критериев с ростом объемов выборок? Всегда ли, например, критерии Шапиро-Уилка и Эппса-Палли по мощности оказываются предпочтительнее?
В этой связи в данной работе методами статистического моделирования исследованы свойства критериев, включенных в ГОСТ Р ИСО 5479-2002: исследованы распределения статистик, мощность критериев по отношению к близким альтернативам, показаны достоинства и недостатки критериев, проведено сравнение по мощности этих критериев с критериями согласия. Исследован ряд критериев, не включенных в стандарт.
Критерий проверки на симметричность [6,7]. Критерий предназначен для проверки
гипотез о симметричности наблюдаемого закона (против наличия асимметрии) при
объемах выборки 
. Статистика критерия имеет вид
,
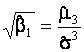(1)
при вычислении которой оценки
используемых центральных моментов (в том числе 
) вычисляются в соответствии с
соотношением
,
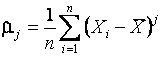где
.
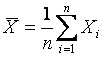Проверяется гипотеза 
: 
=0 против альтернативы 
>0 (положительная
асимметрия) или <0 (отрицательная асимметрия).
В стандарте и первоисточниках [6,7] приводятся только таблицы
процентных точек. Ничего не говорится о виде распределения. Распределение
статистики (1) в случае нормального закона является симметричным и зависит от
числа наблюдений. В [3] говорится, что распределение статистики (1) очень
быстро приближается к нормальному с нулевым математическим ожиданием и
асимптотической дисперсией 
.
В данной работе при исследовании
распределений статистик проверяемой гипотезе всегда соответствует
принадлежность наблюдаемой выборки нормальному закону распределения
.
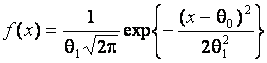При исследовании зависимости
распределений статистик от вида наблюдаемого закона нами рассматривалось целое
множество конкурирующих распределений. Но в тексте работы основные свойства
критериев демонстрируются на альтернативах, позволяющих показать как
достоинства, так и некоторые ранее неизвестные недостатки отдельных критериев.
В качестве таких конкурирующих гипотез при исследовании мощности критериев
рассмотрена принадлежность следующим законам: 
соответствует семейству
распределений с плотностью
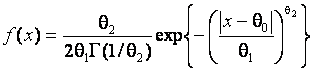(2)
и параметром формы 
; 
– распределению Лапласа с
плотностью
;
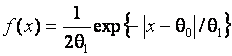– логистическому распределению
,
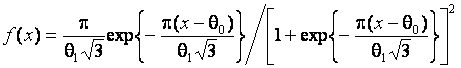очень близкому к нормальному. При
этом, как правило, выборки моделировались с параметром масштаба 
и параметром сдвига 
. Графики функций плотности данных
распределений представлены на рис. 1.
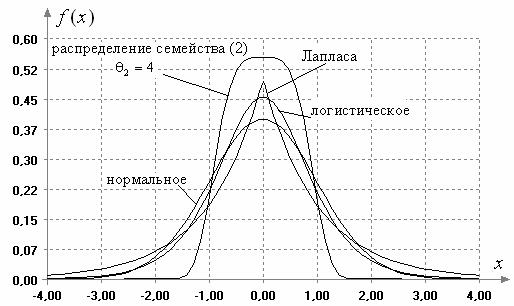
Рис. 1.
Плотности распределений, соответствующих рассматриваемым гипотезам 
Критерий, использующий статистику (1), является только критерием проверки на симметричность. Его использование полезно при проверке отклонений от нормального закона, но неотклонение гипотезы о симметричности на основании предположений о нормальности закона не может служить подтверждением нормальности (условие необходимое, но не достаточное), так как распределение статистики (1) зависит от вида наблюдаемого закона (см. рис. 2).
Нормальное распределение не
единственное симметричное распределение. Поэтому проверяемая гипотеза о
симметричности может необоснованно и отклоняться, и не отклоняться. Например,
в случае принадлежности наблюдаемых выборок распределению семейства (2) с
параметром формы (при справедливости ) и использовании процентных точек для
статистики (1), построенных в предположении нормальности закона, гипотеза о
симметричности не будет отклоняться с бόльшим достигаемым уровнем значимости.
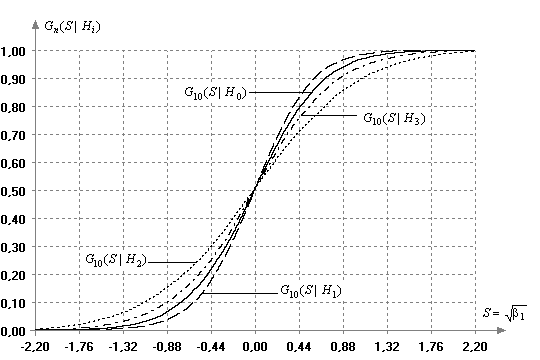
Рис. 2. Распределения статистики критерия
проверки на симметричность в зависимости от гипотез 
при объеме выборок n=10
Критерий проверки на эксцесс [7,8]. В стандарте предусмотрено использование
критерия проверки на эксцесс при объемах выборок . Статистика критерия проверки на
значение эксцесса имеет вид
.
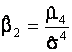(3)
Проверяется гипотеза вида : 
=3 против альтернативы >3 (больший эксцесс) или <3 (меньший эксцесс).
В стандарте и
первоисточниках [7,8] приводятся лишь таблицы процентных точек. Распределение статистики
зависит от объема рассматриваемых выборок. В [3] говорится, что распределение
статистики (3) даже при больших объемах выборок 
оказывается далеким от нормального.
В этом можно убедиться по картине, представленной на рис. 3, где приведены
графики полученных в результате моделирования распределений статистики
критерия проверки на эксцесс в зависимости от объема выборки n.
Распределения статистики (3) были
исследованы при наблюдаемых законах, соответствующих рассмотренным выше
гипотезам . Результаты исследований позволяют судить о мощности
критерия проверки на эксцесс относительно различных альтернатив.
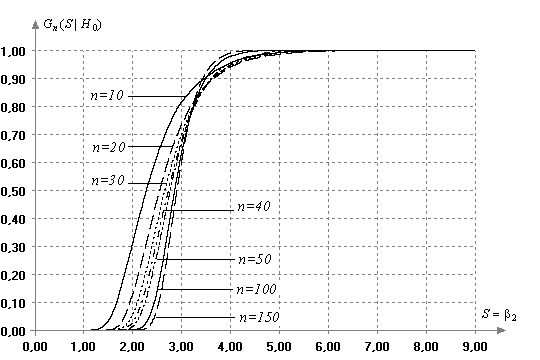
Рис. 3.
Графики распределений статистики критерия проверки на эксцесс в зависимости от
объема выборки при =10,20,40,30,50,100,150
Вместе с критерием симметричности данный критерий позволяет судить о степени отклонения наблюдаемой выборки от нормального закона. Недостатком критерия является сильная зависимость распределения статистики (3) от объема выборок.
Совместный критерий проверки на симметричность и нулевой коэффициент
эксцесса [9] в
стандарте рассматривается при объемах выборок 20££1000 (многонаправленный критерий).
Проверяемая гипотеза имеет вид : =0 и =3 против ≠0 и (или) ≠3. В стандарте приведены
кривые, определяющие критическую область при уровне значимости 
и 
.
В данном случае такой совместный критерий не исследовался. Результаты исследования различных вариантов критериев, построенных на основе (совместного) использования статистик (1) и (3), не вошедших в стандарт, рассмотрены ниже.
Критерий Шапиро-Уилка. Критерий Шапиро-Уилка [10,11], базируется на анализе
линейной комбинации разностей порядковых статистик. В стандарте применение
критерия предусмотрено при объемах выборок 8££50. Сложность применения при больших
объемах выборок затруднена вследствие отсутствия в документе соответствующих
коэффициентов. При объемах выборок 51££99 коэффициенты и таблицы процентных
точек можно найти в [11]. В стандарте критерий рекомендуют применять при
отсутствии априорной информации о типе возможного отклонения от нормальности в
тех случаях, когда в качестве альтернативы можно выбрать гипотезу следующего
вида: примерно симметричное распределение с 
<1/2 и <3 или асимметричное распределение
(например, >1/2). В противном случае рекомендуют критерий Эппса-Палли.
Данная рекомендация неочевидна и требует подтверждения.
При
построении статистики для вариационного ряда 
, полученного по наблюдаемой выборке 
, вычисляют величину
где индекс 
изменяется от 1 до 
или от 1 до 
при четном и нечетном 
соответственно. Коэффициенты 
приведены в стандарте и
первоисточниках [10,11]. Статистика критерия имеет вид
.
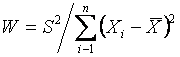(4)
Гипотеза о нормальности отвергается
при малых значениях статистики 
. В стандарте и литературе
отсутствует информация об аналитическом виде распределения статистики,
приводятся лишь процентные точки.
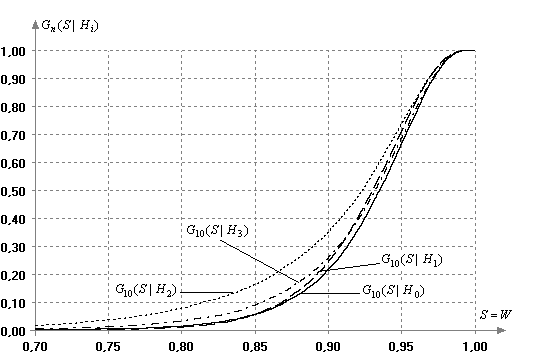
Как и в предыдущих случаях, распределения статистики (4) исследовались методами статистического моделирования. На рис. 4 показана зависимость вида распределения статистики критерия Шапиро-Уилка в зависимости от объема выборки, принадлежащей нормальному закону.
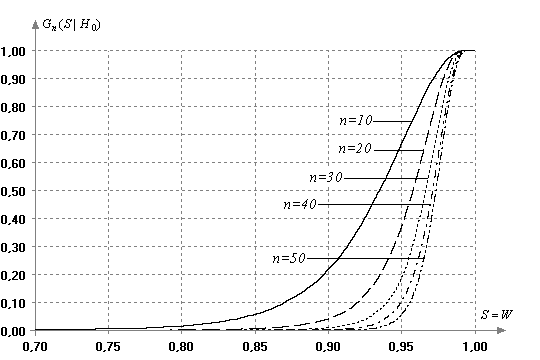
Рис. 4.
Графики распределения статистики критерия Шапиро-Уилка в зависимости от объема
выборки при =10,20,40,30,50
Распределения статистики (4)
исследовались при различных наблюдаемых законах, исследовалась мощность
критерия. В качестве гипотезы рассмотрен нормальный закон
распределения с параметром масштаба равным 1 и параметром сдвига равным 0. В
качестве близких альтернатив рассмотрены гипотезы: – выборка соответствует
семейству распределений (2) с параметром формы равным 4, – распределению Лапласа с
параметрами (0,1), 
– логистическому распределению с параметрами (0,1).
Рис. 5.
Условные распределения 
статистики (3) при справедливости гипотез при
объеме выборок n=10
В качестве примера на рис. 5
приведены полученные условные распределения 
статистики (4) при
справедливости гипотез , , , при объеме выборок =10. Результаты исследований показали,
что при малых объемах выборок (10-20 наблюдений) критерий Шапиро-Уилка не
способен различать гипотезы и . Еще в худшей степени критерий
замечает различие между нормальным распределением и распределением семейства
(2) с параметром формы 
. Более того по отношению к альтернативе критерий оказывается смещенным.
Но с ростом числа наблюдений мощность критерия по распознаванию альтернатив и растет.
Значения мощности
критерия Шапиро-Уилка по отношению к конкурирующим гипотезам ,,
при различных значениях уровня
значимости 
(вероятности ошибки первого рода) приведены соответственно
в таблицах 1-3.
Таблица 1. Мощность критерия Шапиро-Уилка по отношению к распределению семейства (2) с параметром формы 4
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.01 |
0.007 |
0.007 |
0.016 |
0.036 |
0.075 |
|
0.05 |
0.048 |
0.061 |
0.104 |
0.168 |
0.256 |
|
0.075 |
0.080 |
0.102 |
0.162 |
0.244 |
0.333 |
|
0.1 |
0.107 |
0.142 |
0.213 |
0.296 |
0.406 |
Таблица 2. Мощность критерия Шапиро-Уилка по отношению к распределению Лапласа
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.01 |
0.064 |
0.134 |
0.187 |
0.237 |
0.277 |
|
0.05 |
0.152 |
0.266 |
0.334 |
0.375 |
0.418 |
|
0.075 |
0.192 |
0.316 |
0.386 |
0.431 |
0.469 |
|
0.1 |
0.225 |
0.351 |
0.429 |
0.464 |
0.509 |
Как показывают, в том числе, и наши
исследования мощность критериев, специально построенных для проверки
отклонения от нормальности, таких как Шапиро-Уилка и Эппса-Палли, на объемах
выборок ≤50 выше мощности непараметрических критериев согласия
типа Колмогорова, типа 
Крамера-Мизеса-Смирнова и типа 
Андерсона-Дарлинга при проверке
сложных гипотез [12], которые в такой ситуации мощнее критериев типа [13]. С применением критериев
согласия при малых объемах выборок вообще трудно различать близкие альтернативы.
Однако критерии согласия не имеют выявленного в данной работе недостатка,
присущего критериям Шапиро-Уилка и Эппса-Палли: неспособность отличать от нормального
закона распределения семейства (2) с более плоскими плотностями распределений
(с <3).
Таблица 3. Мощность критерия Шапиро-Уилка по отношению к логистическому закону
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.01 |
0.025 |
0.043 |
0.057 |
0.065 |
0.070 |
|
0.05 |
0.081 |
0.116 |
0.130 |
0.138 |
0.142 |
|
0.075 |
0.116 |
0.155 |
0.166 |
0.175 |
0.176 |
|
0.1 |
0.139 |
0.185 |
0.199 |
0.200 |
0.208 |
Критерий Эппса-Палли. Данный критерий [14-17] базируется
на сравнении эмпирической и теоретической характеристических функций. В
стандарте предусмотрено его применение при 8££200. Процентные точки в данном
диапазоне даны с пропусками.
Статистика критерия, вычисляемая по
наблюдаемой выборке , имеет вид
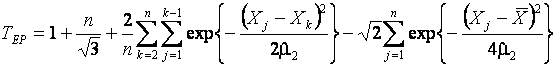, (5)
где ,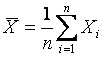 
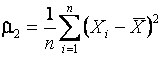. Выборка может быть неупорядочена,
порядок наблюдений произволен, но он должен быть неизменным в течение всех
проводимых вычислений. Гипотезу о нормальности отвергают при больших
значениях статистики.
Распределения статистики (5) исследовались методами
статистического моделирования. На рис. 6 показана зависимость вида распределения
статистики критерия Эппса-Палли в зависимости от
объема выборки, принадлежащей нормальному закону. На рисунке наблюдается
“пучок” распределений. Распределения статистик критерия незначительно меняются
с ростом объемов выборок (в отличие от распределений других рассмотренных здесь
статистик) при нормальном законе распределения случайной величины. С ростом наблюдается быстрая сходимость
распределения статистики к некоторому предельному.
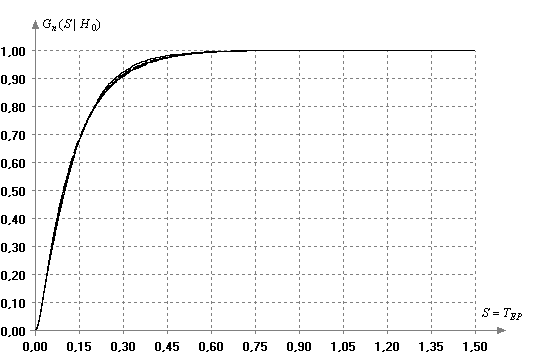
Рис. 6. Графики распределений статистики критерия Эппса-Палли в зависимости от объема выборки при n=10,20,40,30,50,100,150
Процентные точки распределений
статистики (5) при различных объемах выборок отличаются существенно, но
вероятности вида 
, вычисленные по распределениям статистики (5) при различных
n, будут
достаточно близкими. Здесь 
– значение статистики,
полученное по выборке. В частности, распределения статистики критерия
Эппса-Палли при различных объемах выборок достаточно хорошо
аппроксимируются бета-распределениями III рода с функцией плотности
,
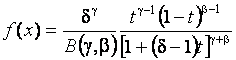где 
. Если пренебречь зависимостью
статистики (5) от объема выборки , то для приближенного вычисления
достигаемого уровня значимости можно использовать бета-распределение
III рода с
параметрами 
=1.8645, 
=2.5155, 
=5.8256, 
=0.9216, 
=0.0008. Соответствующая функция
распределения представляет собой некоторую среднюю для “пучка”
распределений, приведенного на рис.6.
Исследования распределений статистики
критерия Эппса-Палли при справедливости конкурирующих гипотез ,, и оценка мощности критерия по
отношению к данным альтернативам показали, что критерий имеет тот же
недостаток, что и критерий Шапиро-Уилка: он оказывается смещенным относительно
тех же альтернатив. Подтверждением этого является картина, приведенная на рис.
7, где представлены условные функции распределения статистики (5) при
справедливости гипотез , , , при объеме выборок n=10.
При n=10 мощность критерия Эппса-Палли по отношению к гипотезе
меньше (!) уровня значимости
(при 
). Это означает, что при верной гипотезе при проверке нормальности
предпочтение всегда будет отдаваться гипотезе . При n=20 распределения 
и 
в области значений функций
распределения, больших 0.95 практически неразличимы. А при n=50 критерий уже способен различать
гипотезы и .
Значения мощности критерия
Эппса-Палли по отношению к альтернативам ,,, которые можно сравнить с
соответствующими значениями для критерия Шапиро-Уилка, приведены в таблицах
4-6.
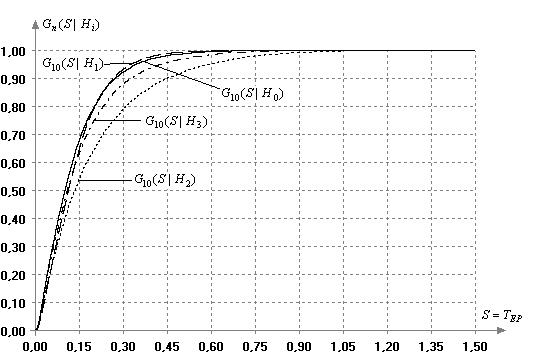
Рис. 7. Условные
распределения статистики (5) при справедливости гипотез при
объеме выборок n=10
По отношению к конкурирующей гипотезе
(логистическому закону) на
объемах выборок ≤50 критерий Эппса-Палли мощнее критерия Шапиро-Уилка
при больших уровнях значимости (
) и уступает критерию Шапиро-Уилка по
мощности при малых уровнях значимости ().
Таблица 4. Мощность критерия Эппса-Палли по отношению к распределению семейства (2) с параметром формы 4
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.1 |
0.091 |
0.126 |
0.183 |
0.222 |
0.281 |
|
0.05 |
0.041 |
0.052 |
0.078 |
0.108 |
0.150 |
|
0.025 |
0.017 |
0.021 |
0.032 |
0.051 |
0.074 |
|
0.01 |
0.006 |
0.007 |
0.010 |
0.015 |
0.025 |
Таблица 5. Мощность критерия Эппса-Палли по отношению к распределению Лапласа
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.1 |
0.243 |
0.354 |
0.462 |
0.552 |
0.623 |
|
0.05 |
0.166 |
0.260 |
0.352 |
0.441 |
0.519 |
|
0.025 |
0.112 |
0.192 |
0.265 |
0.349 |
0.428 |
|
0.01 |
0.066 |
0.128 |
0.175 |
0.257 |
0.323 |
Таблица 6. Мощность критерия Эппса-Палли по отношению к логистическому закону
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
|
0.1 |
0.146 |
0.176 |
0.204 |
0.228 |
0.249 |
|
0.05 |
0.089 |
0.108 |
0.125 |
0.147 |
0.167 |
|
0.025 |
0.052 |
0.070 |
0.083 |
0.097 |
0.112 |
|
0.01 |
0.026 |
0.039 |
0.042 |
0.055 |
0.067 |
Модифицированный критерий
Шапиро-Уилкса.
Необходимость проверки отклонения от нормального распределения, используя несколько
независимых выборок, возникает очень часто, поскольку каждая отдельная выборка
оказывается слишком малой для обнаружения значимого отклонения от нормального
распределения. В такой ситуации при выборках одинакового объема 
стандарт [1] рекомендует
применять модифицированный критерий Шапиро-Уилка.
При проверке для 
последовательных выборок
объемом каждая, отобранных из одной совокупности,
подсчитывается значение 
в соответствии с выражением
.
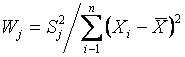Значения 
по соответствующей выборке вычисляются
как и в критерии Шапиро-Уилка, где индекс изменяется от 1 до или от 1 до при четном и нечетном 
соотвеетственно. Коэффициенты
приведены в стандарте и
первоисточниках [6,7]. Для совместного критерия вычисляют значения 
по формуле:
,
где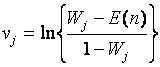 
. Коэффициенты 
, 
и 
для преобразования 
и табулированы [1, 18] и
приведены в стандарте.
Утверждается, что если основное распределение вероятностей нормальное, то
величины приблизительно подчиняются нормальному распределению.
Статистика модифицированного критерия имеет вид
,
(6)
где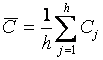 
, и должна подчиняться стандартному
нормальному закону.
Проверяемая гипотеза о принадлежности выборок нормальному закону отклоняется при
уровне значимости , если 
, где 
– -квантиль стандартного нормального распределения. Заметим,
что в тексте стандарта [1] ошибка в формуле (19).
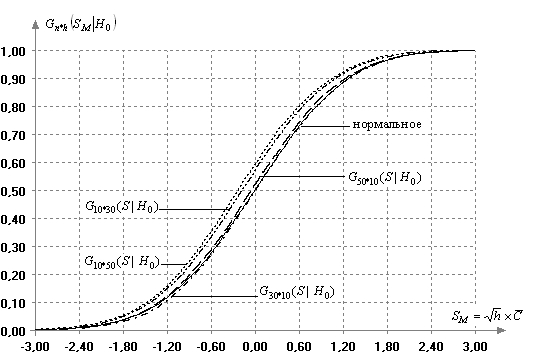
Рис. 8. Условные распределения 
статистики (6) при различных
комбинациях и
К сожалению, наши исследования
показали, что распределение статистики (6) лишь очень приближенно подчиняется стандартному
нормальному закону и зависит от и . При конкретных комбинациях и условное распределение
статистики может существенно отличаться от стандартного
нормального закона, что является существенным недостатком критерия. Как
правило, функция распределения статистики оказывается сдвинутой влево от
стандартного нормального распределения. Таким образом, принимая решение на
основании процентных точек стандартного нормального закона в соответствии с , мы можем несправедливо отклонить
верную гипотезу . То есть, вероятность ошибки первого рода на самом деле
оказывается больше задаваемого . На рис. 8 в качестве примера
приведены распределения статистики при различных комбинациях и . Здесь же для сравнения представлена
функция распределения стандартного нормального закона.
Исследования показали,
что модифицированный критерий Шапиро-Уилка, как и другие, при малых n*h (20-30 наблюдений в совокупности)
не способен различить гипотезы и (отличить нормальный закон от
семейства (2) с параметром ). Кроме того, модифицированный
критерий Шапиро-Уилка при малых n*h<100 уступает по мощности критериям
Эппса-Палли и Шапиро-Уилка, уступает он и непараметрические критериям согласия.
Совокупность недостатков критерия позволяет не рекомендовать его для
применения.
Совместный критерий проверки на симметричность и нулевой коэффициент эксцесса. Далее рассмотрен ряд критериев, не имеющих отношения к стандарту [1], статистики которых измеряют отклонения от нормальности, как правило, с использованием отклонений статистик (1) и (3) от значений, соответствующих нормальному закону. В [9] и [19], где приводятся полезные сведения о ряде критериев проверки отклонения от нормального закона, рассмотрена одномерная статистика на базе статистик (1) и (3)
,
(7)
которая асимптотически
распределена как 
-распределение. В качестве нормирующих коэффициентов в ней
взяты первые члены асимптотических дисперсий асимптотически нормальных
распределений статистик (1) и (3) [3].
Наши исследования распределений
статистики (7) при различных объемах выборок показали, что они настолько плохо
сходятся к асимптотическому предельному -распределению, что последним обоснованно
можно пользоваться лишь при объемах выборок, превышающих несколько тысяч
наблюдений.
Модификация D’Agostino критерия
проверки на симметричность. В работе [6] предложена модификация критерия проверки симметричности.
В данной модификации на основании следующих соотношений статистика (1)
преобразуется в статистику 
, приближенно подчиняющуюся
стандартному нормальному закону:
, 
,
,
,
.
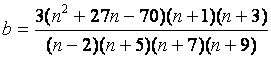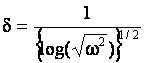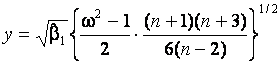(8)
Исследования распределений статистики (8) при различных объемах выборок показали, что они очень хорошо согласуются со стандартным нормальным законом.
Модификация D’Agostino критерия
проверки на симметричность и значение эксцесса. В [6] с помощью следующих
соотношений предложено преобразование статистик (3) и (1) к статистике 
, приближенно распределенной в
соответствии со стандартным нормальным законом:
, 
.
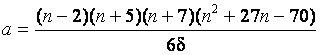
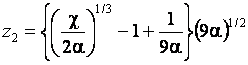(9)
Исследования
распределений статистики (9) при справедливой гипотезе и различных объемах выборок
показали, что 
достаточно хорошо согласуются со стандартным
нормальным законом (несколько хуже, чем , но хорошо). Критерий
двусторонний: проверяемая гипотеза отклоняется, если 
или 
.
Исследование мощности
критерия со статистикой (9) по отношению к альтернативам , , (и ряду других) показало, что
данный критерий оказывается мощнее всех рассмотренных критериев. Значения
мощности критерия относительно альтернатив , , при различных объемах выборок
представлены в таблицах 7-9.
Таблица 7.
Мощность критерия со статистикой 
по отношению к распределению
семейства (2) с параметром формы (по нижним процентным точкам)
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
n=100 |
n=300 |
|
0.1 |
0,184 |
0,251 |
0,350 |
0,438 |
0,520 |
0,835 |
1 |
|
0.05 |
0,097 |
0,124 |
0,181 |
0,245 |
0,315 |
0,666 |
0,998 |
|
0.025 |
0,051 |
0,059 |
0,084 |
0,116 |
0,166 |
0,469 |
0,991 |
|
0.01 |
0,023 |
0,019 |
0,025 |
0,036 |
0,058 |
0,245 |
0,960 |
Достоинством критерия со статистикой (9) является возможность использования в качестве предельного распределения стандартного нормального закона. Статистика критерия учитывает отклонения от симметричности и от эксцесса нормального распределения.
Таблица 8. Мощность критерия со статистикой по отношению к распределению
Лапласа (по верхним процентным точкам)
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
n=100 |
n=300 |
|
0.1 |
0.193 |
0.312 |
0.411 |
0.488 |
0.574 |
0.815 |
0.995 |
|
0.05 |
0.113 |
0.223 |
0.311 |
0.389 |
0.469 |
0.742 |
0.992 |
|
0.025 |
0.068 |
0.163 |
0.240 |
0.309 |
0.391 |
0.671 |
0.987 |
|
0.01 |
0.035 |
0.106 |
0.174 |
0.230 |
0.307 |
0.588 |
0.978 |
Таблица 9. Мощность критерия со статистикой по отношению к логистическому
распределению (по верхним процентным точкам)
|
|
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
n=100 |
n=300 |
|
0.1 |
0.131 |
0.188 |
0.234 |
0.270 |
0.320 |
0.680 |
0.851 |
|
0.05 |
0.071 |
0.117 |
0.158 |
0.188 |
0.229 |
0.771 |
0.780 |
|
0.025 |
0.039 |
0.074 |
0.110 |
0.131 |
0.171 |
0.829 |
0.711 |
|
0.01 |
0.018 |
0.045 |
0.067 |
0.086 |
0.115 |
0.885 |
0.621 |
При малых и близких альтернативах
критерий превосходит по мощности критерии Шапиро-Уилка и Эппса-Палли. В отличие
от всех рассмотренных данный критерий способен успешно отличать от нормального
закона распределения семейства (2) с более плосковершинными по сравнению с
нормальным законом плотностями.
Совместный критерия проверки на
симметричность и нулевой коэффициент эксцесса D’Agostino. На базе статистик и в [6] рассмотрена одномерная
статистика вида
,
(10)
приближенно распределенная как -распределение. Проверяемая гипотеза
о нормальности отклоняется при больших значениях статистики (10).
Исследование распределений данной
статистики показало, что в отличие от статистики (7) распределение статистики
(10) очень хорошо согласуется с -распределением уже при достаточно
малых . По отношению к альтернативам и критерий не уступает по
мощности критериям Шапиро-Уилка и Эппса-Палли. Однако он обладает и тем же самым
недостатком: при малых данный критерий не позволяет надежно различать
гипотезы и вследствие смещенности (см. рис. 9).
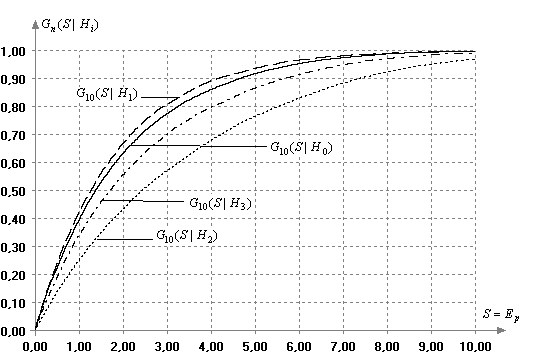
Рис. 9.
Условные распределения статистики (10) в зависимости от вида наблюдаемого
закона, соответствующего различным , при n=10
Заключение.
Использование критериев согласия для проверки отклонений от нормального закона при малых объемах выборок является бесперспективным вследствие их очень низкой мощности в такой ситуации по отношению к близким альтернативам [3, 20, 21, 12]. Совсем другое дело, при больших n. При малых n предпочтение необходимо отдать специальным критериям проверки отклонений от нормальности.
Критерий Эппса-Палли при близких альтернативах по мощности не уступает критерию Шапиро-Уилка.
Недостатком критериев Шапиро-Уилка, Эппса-Палли и критерия со статистикой (10), который ранее никем не отмечался, является их смещенность при малых объемах выборок по отношению к альтернативам, более плосковершинным по сравнению с нормальным законом (со значением эксцесса меньшим 3), то есть неспособность отличить эти альтернативы от нормального закона.
Модифицированный критерий Шапиро-Уилка, рекомендованный стандартом [1], нецелесообразно использовать из-за очень плохой сходимости распределения статистики к предельному и повышенной вследствие этого вероятности ошибок первого рода.
Критерием, по крайней мере, не уступающим по мощности при близких альтернативах критериям Шапиро-Уилка и Эппса-Палли, у которого отсутствует недостаток, свойственный последним, является критерий со статистикой (9), который целесообразно рекомендовать для применения.
Проверка отклонения распределения от нормального закона имеет особое значение. Далеко не всегда ошибки измерений, связанные с приборами, построенными на конкретных физических принципах, или ошибки наблюдений контролируемого показателя подчиняются нормальному закону [22, 23]. В таких случаях применение классического аппарата, опирающегося на предположение о нормальности наблюдаемого закона, оказывается некорректным и может приводить к неверным выводам.
В основе исследований, проведенных в данной работе, лежит развиваемый подход численного исследования рекомендаций математической статистики, опирающийся на развиваемое программное обеспечение статистического анализа, статистического моделирования и исследования статистических закономерностей, хорошо зарекомендовавший себя в предшествующих работах [20, 21, 24]. В процессе исследований распределений статистик закономерности строились (и проверялись) по десяткам и сотням тысяч экспериментов.
Работа выполнена при финансовой поддержке Минобразования РФ (проект Т02-3.3-3356)
Более подробная информация о результатах данных исследований доступна по адресу http://www.ami.nstu.ru/~headrd/seminar/Kontrol_Q/ krit_zad.htm.
1. ГОСТ Р ИСО 5479-2002. Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения. - М.: Изд-во стандартов. 2002. - 30 с.
2. Золотухина Л.В., Винник Е.В. Эмпирическое исследование мощности критерия Саркади и его модификация // Заводская лаборатория. 1985. - Т. 51. - №1. – С. 51-55.
3. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
4. Shapiro S.S, Wilk M.B., Chem C.J. J. Amer.
Stat. Ass., 1968. December. – P.1343-1372.
5. Pearson E.S..,
D’Agostino R.B., Bowmann K.O. Test for departure from normality: Comparison of
powers // Biometrika, 64, 1977. – P.231-246.
6. D’Agostino
R.B. Transformation to normality of the null distribution of g1 //
Biometrika, 57, 1970. – P.679-681.
7. Pearson
E.S., Hartley H.O. Biometrika tables for Statisticians. Vol. 1, edn. 3, Cambridge
University Press, 1966. – P.207-208.
8. D’agostino
R.B., Tietjen G.L. Simulation probability points of b2 for small
samples // Biometrika, 58, 1971. – P.669-672.
9. Bowmann
K.O., Shenton L.R. ‘Omnibus’ test contours for departures from normality based
on 
// Biometrika, 62, 1975. – P.243-250.
10. Shapiro S.S.,
Wilk M.B. An analysis of variance test for normality (complete samples) //
Biometrika, 52, 1965. – P.591-611.
11. Shapiro S.S., Francia R.S. An appriximate analysis of variance test fo normality // J. Amer. Statist. Assoc., 337, 1972. – P.215-216.
12. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. - М.: Изд-во стандартов. 2002. - 64 с.
13. Р 50.1.033-2001. Рекомендации по
стандартизации. Прикладная статистика. Правила проверки согласия опытного
распределения с теоретическим. Часть I. Критерии типа хи-квадрат. - М.: Изд-во
стандартов. 2002. - 87 с.
14. Baringhaus
L., Danschke R., Henze N. Recent and classical tests for normality – A
comparative study. Comm. Statistic. B, 18(1), 1989. – P.363-379.
15. Baringhaus
L., Henze N. A consistent test for multivatiate normality based on the
emperical characteristic function // Metrika. 35, 1988. – P.339-348.
16. Epps
T.W., Pulley L.B. A test for normality based on the empirical characteristic
function // Biometrika. 70, 1983. – P. 723-726.
17. Henze
N. An approximation to the limit distribution of the Epps-Pulley test statistic
for normality // Metrika. 37, 1990. – P.7-18.
18. Pearson E.S.,
Hartley H.O. Biometrika tables for Statisticians. Vol. 2, Cambridge
University Press, 1976. – P.221.
19. Doornik
J.A., Hansen H. An Omnibus Test for Univariate and Multivariate Normality.
1994. (http://www.nuff.ox.ac.uk/users/Doornik/papers/ normal2.pdf)
20. Лемешко Б.Ю., Постовалов С.Н. О зависимости распределений статистик непараметрических критериев и их мощности от метода оценивания параметров // Заводская лаборатория. Диагностика материалов. 2001. - Т.67. - № 7. - С. 62-71.
21. Лемешко Б.Ю., Постовалов С.Н. Применение непараметрических критериев согласия при проверке сложных гипотез // Автометрия. 2001. - № 2. - С. 88-102.
22. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомизд., 1991. - 303 с.
23. Орлов А.И. Часто ли распределение результатов наблюдений является нормальным // Заводская лаборатория. 1991. - Т. 57. - №7. – С. 64-66.
24. Лемешко Б.Ю., Чимитова Е.В. Оптимальные L-оценки параметров сдвига и масштаба распределений по выборочным квантилям // Заводская лаборатория. Диагностика материалов. 2004. – Т.70. – №1. – С. 54-66.