См. также: Прикладная математическая статистика (материалы к семинарам)

Заводская лаборатория. Диагностика материалов. 2004. Т. 70,  № 1. С.54-66

УДК 519.24

ОПТИМАЛЬНЫЕ L-ОЦЕНКИ ПАРАМЕТРОВ СДВИГА И МАСШТАБА РАСПРЕДЕЛЕНИЙ ПО ВЫБОРОЧНЫМ КВАНТИЛЯМ[1]

Б.Ю. Лемешко, Е.В. Чимитова[2]

Исследуются свойства L-оценок параметров сдвига и масштаба в виде линейных комбинаций выборочных квантилей. Предлагается использовать для построения таких оценок выборочные квантили, соответствующие асимптотически оптимальному группированию, при котором минимизируются потери в информации Фишера. Построены таблицы коэффициентов L-оценок параметров для ряда законов распределений, позволяющие просто вычислять оптимальные L-оценки. Методами статистического моделирования показано, что предельными распределениями статистики критерия согласия  Пирсона в случае использования L-оценок являются -распределения. Рекомендуется применение L-оценок для оперативного анализа больших объемов данных.

Введение. L-оценки параметров распределений формируются как линейные комбинации порядковых статистик или выборочных квантилей. Такие оценки обладают двумя важными для  практического применения качествами: простотой вычислений и хорошими свойствами робастности.

Исследованию оценок, опирающихся на порядковые статистики, посвящено большое число зарубежных работ, итоги которых на определенных этапах аккумулированы в сборнике [1] и монографии [2], а также целый ряд отечественных публикаций, например, [3-6]. Хороший обзор результатов по линейным комбинациям порядковых статистик представлен в работе [7].

При больших объемах выборок строить L-оценки с использованием всего множества порядковых статистик весьма затруднительно и более экономично для вычисления оценок параметров воспользоваться выборочными квантилями. Многочисленные модификации ме-тода квантилей эффективно используется при различной форме регистрации наблюдений [8].

В данной работе мы остановимся на L-оценках параметров сдвига и масштаба, вычисление которых базируется на значениях выборочных квантилей [1]. Самой сложной операцией при вычислении таких оценок является сортировка имеющейся выборки по возрастанию с целью определения выборочных квантилей наблюдаемого закона. Как и оценки максимального правдоподобия по группированным наблюдениям [9, 10], данные оценки являются робастными. Под робастностью в статистике понимают нечувствительность к малым отклонениям от предположений [11]. Робастность этих оценок подтверждает вид функций влияния Хампеля [12], которые для L-оценок представляют собой ступенчатые, ограниченные по абсолютной величине зависимости [11, 13]. Такой вид функций влияния говорит о том, что присутствие в выборке аномальных наблюдений не будет приводить к резкому изменению L-оценок. 

Коэффициенты в линейной комбинации L-оценок определяются тем, какие и сколько квантилей используются при построении оценок. От выбора квантилей при построении оценок зависят и асимптотические свойства получаемых L-оценок.

Построение L-оценок параметров сдвига и масштаба. Дз. Огавой, опираясь на асимптотическое распределение выборочных квантилей ( квантилей при  интервалах) [14], в работах [15, 1] получено асимптотическое распределение выборочных квантилей для законов, определяемых только параметрами сдвига  и масштаба , с функцией распределения  и функцией плотности . Им же (см. стр. 54-60, [1]) методом наименьших квадратов построены “оптимальные линейные несмещенные оценки” параметров сдвига и масштаба, в основе которых лежат значения выборочных квантилей.

При построении оценок используются квантили  рассматриваемого закона, которые делят область определения случайной величины в соответствии с заданными вероятностями  попадания наблюдений в интервалы, где .

            Выражения для оценок [15, 1] можно преобразовать в совсем простые зависимости [16, 17]. При известном параметре L-оценка параметра  принимает вид

,                                                              (1)

где , , – оценки квантилей по наблюдаемой выборке, которые при заданных вероятностях , , …,  зависят от параметров  и  наблюдаемого закона.

L-оценка параметра  при известном  принимает вид

.                                                             (2)

            При одновременном оценивании параметров сдвига и масштаба выражения для L-оценок параметров имеют вид

,                                                                     (3)

.                                                                     (4)

            Выбор квантилей  стандартного распределения и вычисление , , , .  Значения коэффициентов , , ,  в формулах (1)-(4) зависят от выбора квантилей  стандартного распределения (от выбора вероятностей , , …, ). L-оценки (1)-(4) являются асимптотически эффективными [1]. Асимптотическая дисперсионная матрица вектора L-оценок параметров  определяется соотношением

,                                                              (5)

где  – информационная матрица Фишера вектора параметров распределения по группированным наблюдениям.

Так как рассматриваемые оценки асимптотически эффективны, то использование квантилей (граничных точек интервалов), соответствующих асимптотически оптимальному группированию, при котором минимизируются потери в информации Фишера, связанные с группированием [18, 19], обеспечивает оптимальные свойства этих оценок [18]: минимум асимптотической дисперсии, а в случае оценивания сразу двух параметров – минимум обобщенной асимптотической дисперсии.

В частных случаях решение задачи оптимального выбора квантилей для построения L-оценок рассматривалось в ряде работ. В [1, 20] рассматривались оценки параметров для нормального распределения, в [1] - для однопараметрического экспоненциального распределения, в [21] - для двухпараметрического экспоненциального распределения, в [22] – для параметров логистического распределения, в [23] - для параметров распределения Коши, в [24] - для параметров распределения экстремальных значений. Приближенный подход к решению такой задачи рассматривался в [25]. Причем в случае одновременного оценивания параметров  и  оптимальные наборы граничных точек определялись исходя из минимума величины , , а не минимума , как в [19].

            Опираясь на построенную нами совокупность таблиц асимптотически оптимального группирования [19, 26, 27], значения коэффициентов , , ,  при различном числе используемых квантилей для параметров законов распределений, упоминаемых в данной статье, получены в [16] (64 таблицы) и вместе с таблицами асимптотически оптимального группирования (58 таблиц) доступны читателям журнала на WEB-сайте [28].

Таблицы коэффициентов для формул вида (1), (2), (3) и (4) сформированы для нормального распределения, для логистического распределения с функцией плотности

,

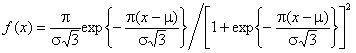для распределения Коши с плотностью

,

для распределения наименьшего экстремального значения с плотностью

,

для распределения наибольшего экстремального значения с плотностью

.

При этом в зависимости от того, известен ли один из параметров или неизвестны оба параметра, наборам коэффициентов ,  и паре ,  соответствуют свои таблицы асимптотически оптимального группирования. В частности, некоторые асимптотически оптимальные граничные точки  для случая одновременного оценивания двух параметров нормального распределения представлены в табл. 1, а соответствующие вероятности – в табл. 2. В последнем столбце таблиц приведены значения относительной асимптотической информации, представляющей собой отношение определителя информационной матрицы Фишера по группированным данным к определителю информационной матрицы Фишера по негруппированным . Данная величина позволяет судить о потерях информации, связанной с группированием. Полученные значения коэффициентов , приведены в табл. 3 - 4.

Для распределений экспоненциального с плотностью

,

модуля нормального вектора () с плотностью

,

частными случаями которого являются распределения полунормальное - , Рэлея -  и Максвелла - , таблицы коэффициентов , ,  опираются на таблицы асимптотически оптимального группирования только относительно масштабного параметра . Это связано с тем, что область определения этих случайных величин зависит от параметра сдвига .

Таблица 1

Оптимальные граничные точки интервалов группирования в виде  для одновременного оценивания двух параметров нормального распределения и проверки согласия по критерию  Пирсона

k	t1	t2	t3	t4	t5	t6	t7	t8	A
3	-1,1106	1,1106							0,4065
4	-1,3834	0,0	1,3834						0,5527
5	-1,6961	-0,6894	0,6894	1,6961					0,6826
6	-1,8817	-0,9970	0,0	0,9970	1,8817				0,7557
7	-2,0600	-1,2647	-0,4918	0,4918	1,2647	2,0600			0,8103
8	-2,1954	-1,4552	-0,7863	0,0	0,7863	1,4552	2,1954		0,8474
9	-2,3188	-1,6218	-1,0223	-0,3828	0,3828	1,0223	1,6218	2,3188	0,8753

Таблица 2

Вероятности попадания наблюдений в интервалы при асимптотически оптимальном группировании в случае одновременного оценивания двух параметров нормального распределения или проверки согласия по критерию  Пирсона

k	P1	P2	P3	P4	P5	P6	P7	P8	P9	A
3	0,1334	0,7332	0,1334							0,4065
4	0,0833	0,4167	0,4167	0,0833						0,5527
5	0,0449	0,2004	0,5094	0,2004	0,0449					0,6826
6	0,0299	0,1295	0,3406	0,3406	0,1295	0,0299				0,7557
7	0,0197	0,0833	0,2084	0,3772	0,2084	0,0833	0,0197			0,8103
8	0,0141	0,0587	0,1431	0,2841	0,2841	0,1431	0,0587	0,0141		0,8474
9	0,0102	0,0422	0,1009	0,1976	0,2982	0,1976	0,1009	0,0422	0,0102	0,8753

Таблица 3

Коэффициенты параметра сдвига. Нормальное распределение, неизвестны оба параметра.

k	g1	g2	g3	g4	g5	g6	g7	g8
3	0,500000	0,500000
4	0,224374	0,551252	0,224374
5	0,108579	0,391421	0,391421	0,108579
6	0,067815	0,234061	0,396249	0,234061	0,067815
7	0,043180	0,141936	0,314884	0,314884	0,141936	0,043180
8	0,029871	0,096902	0,216939	0,312575	0,216939	0,096902	0,029871
9	0,021547	0,068108	0,148605	0,261739	0,261739	0,148605	0,068108	0,021547

            Симметричность коэффициентов в формулах (1), (2), (3) и (4) для симметричных распределений определяется симметричностью оптимальных граничных точек интервалов. В книге [2] при обзоре работ по построению рассматриваемых L-оценок, было высказано предположение о симметричности оптимальных квантилей для параметра  нормального распределения. Однако для параметров масштаба при известном параметре сдвига и четном  задача асимптотически оптимального группирования обычно имеет два решения с несимметричными значениями квантилей. В таких случаях пара этих решений зеркальна относительно центра симметрии распределения. Поэтому не единственным является оптимальный набор коэффициентов в формулах (2).

Таблица 4

Коэффициенты масштабного параметра. Нормальное распределение, неизвестны оба параметра.

k	u1	u2	u3	u4	u5	u6	u7	u8
3	-0,450207	0,450207
4	-0,361428	0	0,361428
5	-0,201360	-0,229872	0,229872	0,201360
6	-0,140732	-0,235892	0	0,235892	0,140732
7	-0,095717	-0,186279	-0,136715	0,136715	0,186279	0,095717
8	-0,070411	-0,147147	-0,166972	0	0,166972	0,147147	0,070411
9	-0,052747	-0,114684	-0,153492	-0,090860	0,090860	0,153492	0,114684	0,052747

Для вычисления предлагаемых оптимальных L-оценок достаточно в соотношения (1), (2) или (3) и (4) с известными коэффициентами [28] подставить значения выборочных квантилей , которые определяются таким образом, чтобы имеющаяся выборка оказалась разбитой на части с числом наблюдений , пропорциональным вероятности  попадания в соответствующий интервал при асимптотически оптимальном группировании ().  То есть,  должно быть выбрано из условия

,

где  - члены вариационного ряда , построенного по исходной выборке, ,  - означает целую часть числа, а  - выбираются из соответствующей строки таблицы оптимальных вероятностей. Например, в качестве  могут быть взяты средние значения между соответствующими соседними членами вариационного ряда.

Асимптотические свойства L-оценок тем лучше, чем большее количество выборочных квантилей в них использовано. Практически количество используемых квантилей (число интервалов) ограничивается сверху объемом выборки и следующими соображениями. Во-первых, очевидно, что число интервалов  следует выбирать так, чтобы минимальное произведение  при данном  было больше 1 (3-5, но лучше больше 5-10). Это связано с ожидаемым числом попадания наблюдений, как правило, в крайние интервалы и определяет возможность определения соответствующей выборочной квантили. Во-вторых, число интервалов  ограничивается сверху максимальным числом интервалов, для которого построены соответствующие таблицы асимптотически оптимального группирования [19, 26, 27, 28]. Для случая оценивания одного параметра величина  ограничена 10-11 интервалами, для случая двух параметров – 15 интервалами. Использование большего числа интервалов нецелесообразно в связи с тем, что в первом случае в группированной выборке сохраняется 94-98% информации Фишера (это соответствует увеличению среднеквадратического отклонения оценки по группированным наблюдениям по сравнению с оцениванием по негруппированным на 3-1%), а во втором случае – порядка 95% информации.

Например, при необходимости оценивания по выборке 2-х параметров нормального закона, исходя из рекомендаций  для интервала с минимальной вероятностью попадания и опираясь на табл. 2 (вариант полной таблицы см. в [19, 26, 27, 28]), мы получим рекомендуемые значения числа интервалов, представленные в табл. 5.

Таблица 5

Рекомендуемые значения числа интервалов при оценивании по выборке 2-х параметров нормального закона в зависимости от объема выборки

Объем выборки n	Число интервалов k	Объем выборки n	Число интервалов k
≤37	3	390÷650	≤10
36÷60	≤4	510÷850	≤11
67÷111	≤5	640÷1070	≤12
100÷167	≤6	810÷1350	≤13
152÷254	≤7	1000÷1670	≤14
213÷355	≤8	1200 и более	≤15
294÷490	≤9

            Таким образом, вся процедура вычисления L-оценок состоит в построении по имеющейся выборке вариационного ряда, определении  и выполнении десятка арифметических операций по формулам (1), (2) или (3) и (4). Причем с ростом объема выборки растет лишь число операций, требуемое для сортировки выборки по возрастанию.

Пример. Для нормального распределения при  соотношение (1) принимает вид (см. [16, 17,  28])

,

соотношение (2) (см. [16, 17, 28]) –

,

соотношения (3) и (4) (см. табл. 3-4) –

,

.

            Если мы оцениваем оба параметра, для определения  вероятности  выбираются из табл. 2. И при объеме выборки в 1000 наблюдений в качестве , , можно взять средние значения между следующими парами членов вариационного ряда: , , , , , , , .

Точность оценивания квантилей и L–оценок. Оптимальные L-оценки параметров сдвига и масштаба являются асимптотически эффективными. На практике же мы имеем дело с выборками ограниченного объема. Понятно, что и точность оценивания квантилей , и точность вычисления L-оценок зависят от объема выборки . В качестве основного возражения против использования L-оценок обычно выдвигают возможную значительную неточность в определении выборочных квантилей , которая должна отражаться на точности L-оценок.

Методами статистического моделирования нами были исследованы законы распределения выборочных квантилей и получаемых L-оценок в зависимости от конкретных объемов выборок  и числа используемых квантилей для различных законов наблюдаемых случайных величин. Например, на рис. 1 приведены центрированные плотности выборочных квантилей  и L-оценок , построенных по этим выборочным квантилям. Плотности центрированы относительно истинных значений квантилей  и параметра . Рассматривался случай оценивания масштабного параметра  экспоненциального закона при использовании 5 квантилей (число интервалов ) при объемах выборок . Экспоненциальный закон моделировался с масштабным параметром . Значения асимптотически оптимальных квантилей , , для данной ситуации соответственно равны [19, 26-28] 0,4993; 1,0997; 1,8538; 2,8714; 4,4650. А значения соответствующих вероятностей попадания в интервалы между  – 0,3930; 0,2740; 0,1763; 0,1000; 0,0451; 0,0116. Значение L-оценки  определялось по формуле:

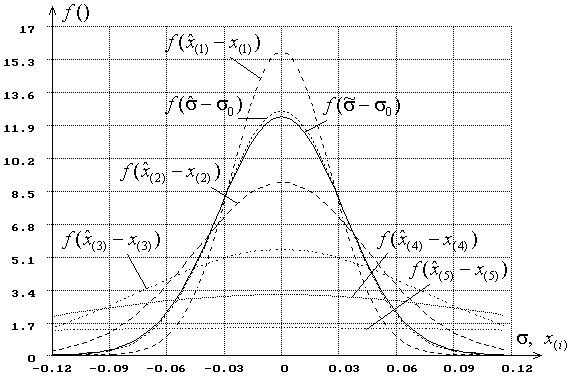
Рис. 1. Центрированные плотности распределения выборочных асимптотически

оптимальных квантилей и L-оценок масштабного параметра экспоненциального

распределения при объемах выборок

Для построения приведенных на рисунке законов распределения формировались выборки оценок из  значений, каждое из которых находилось по выборке объема  случайных величин, распределенных по экспоненциальному закону. Представляемые плотности построены по ансамблю реализаций (усреднены по 100 экспериментам). То есть, общий объем смоделированных оценок, по которому строилось соответствующее распределение на рис. 1, составлял величину 2000´100=200000 наблюдений.

Для моделируемых эмпирических распределений наилучшими моделями оказался нормальный закон. О степени близости к нормальному закону эмпирических распределений L-оценок можно судить по усредненным (по 10 экспериментам) значениям статистик  критериев согласия типа c² Никулина [27, 29–31], типа Колмогорова [32], типа  w² Мизеса [32], типа W² Андерсона–Дарлинга [32] и соответствующим вероятностям  (достигаемому уровню значимости), получаемым при проверке сложных гипотез (см. табл. 6).

Для сравнения на рисунке построена также плотность асимптотического распределения оценки максимального правдоподобия (ОМП)  по точечной выборке (по негруппированным наблюдениям). Сравнивая плотность асимптотически эффективной ОМП по точечной выборке с плотностью L-оценки, мы видим, что последние мало уступают ОМП. Это естественно, так как в данном случае при асимптотически оптимальном группировании сохраняется 94,76% информации Фишера о параметре масштаба . Следовательно, стандартное отклонение предельного распределения  превышает стандартное отклонение распределения  не более чем на 2,73%.

Таблица 6

Усредненные значения статистик критериев

 согласия и достигаемый уровень значимости при проверке

 сложных гипотез о согласии с нормальным законом

Критерий	Значение статистики критерия
Никулина типа c^2	1,09009	0,8958
Типа Колмогорова	0,52249	0,7490
Типа w^2 Мизеса	0,04516	0,5877
Типа W^2 Андерсона– Дарлинга	0,43316	0,2903

Рисунок наглядно демонстрирует, что, несмотря на относительно невысокую точность оценивания квантилей ,  и , мы имеем достаточно высокую точность оценивания параметра масштаба  наблюдаемого экспоненциального закона. При этом, очевидно, что эти оценки не многим уступают ОМП по негруппированным наблюдениям, имея существенное преимущество в робастности.

О точности статистического моделирования можно судить, например, по следующим фактам. Стандартное отклонение теоретического асимптотического нормального распределения  (для ОМП по негруппированным наблюдениям при объеме выборки  и значении =1), определяемое из соотношения , равно 0,031623. Стандартное отклонение распределения , построенного в результате моделирования, также нормального, равно 0,0316. По существу, распределение, полученное в результате моделирования, совпадает с асимптотическим Аналогично для L-оценок стандартное отклонение асимптотического нормального распределения , определяемое соотношением (5), равно 0,032465. А для соответствующего распределения, полученного в результате моделирования и представленного на рис. 1, стандартное отклонение равно 0,0324. В обоих случаях наблюдаем совпадение трех значащих цифр.

Точность L-оценок в зависимости от объема выборок. В связи с потерей информации при группировании L-оценки имеют большее рассеяние, чем асимптотически эффективные оценки, построенные по негруппированным данным. Например, в табл. 7 показан % увеличения среднего квадратического отклонения асимптотического распределения L-оценок по сравнению со средним квадратическим отклонением асимптотически эффективных оценок по негруппированным наблюдениям в зависимости от числа интервалов  для параметров сдвига и масштаба нормального закона (при оценивании только одного из них). Эти значения характеризуют асимптотическую точность оценивания.

Состоятельность оценок и характер изменения точности L-оценок с ростом конечного объема выборок  при фиксированном числе используемых квантилей демонстрирует рис. 2. На рисунке приведены плотности оценок  параметра нормального закона, центрированные относительно истинных значений параметра , для случая  в зависимости от , когда при построении L-оценок используются всего две выборочных квантили, соответствующие асимптотически оптимальному группированию, при одновременном оценивании параметров  и . Выборки нормального закона объема  генерировались с параметрами  и .

                                                                                                       Таблица 7

Увеличение среднего квадратического отклонения асимптотического распределения L-оценок по сравнению с асимптотически эффективными оценками по негруппированным наблюдениям

k	Для параметра сдвига ( в %)	Для параметра масштаба (в %)
2	25,63	81,31
3	11,12	23,83
4	6,45	16,58
5	4,25	10,14
6	3,03	7,91
7	2,28	5,74
8	1,77	4,73
9	1,42	3,73
10	1,16	3,18

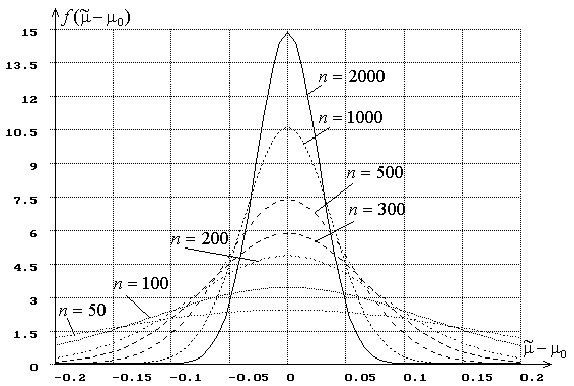
Рис. 2. Плотности распределения L-оценок  при  в зависимости от

О сравнительной точности оценивания можно судить по значениям среднеквадратичного отклонения закона, описывающего распределение соответствующих оценок при конкретных объемах выборок. Значения среднего квадратичного отклонения характеризуют рассеяние оценок. Например, в табл. 8 для различных объемов выборок представлены значения среднеквадратичных отклонений (СКО) для ОМП по негруппированным наблюдениям  и  и для L-оценок  и  параметров сдвига и масштаба логистического закона при . Характеристики рассеяния для ОМП по группированным наблюдениям в данном случае совпадают с характеристиками рассеяния L-оценок.

Таблица 8

Объем выборки	ОМП по точечной выборке		L-оценки
	СКО	СКО	СКО	СКО
100	0,0947	0,0833	0,0997	0,0927
300	0,0550	0,0482	0,0577	0,0541
500	0,0426	0,0373	0,0446	0,0420
1000	0,0301	0,0264	0,0315	0,0297
2000	0,0214	0,0187	0,0224	0,0210

L-оценки асимптотически эквивалентны ОМП по группированным наблюдениям: асимптотические дисперсионные матрицы этих оценок определяются соотношением (5). Однако при конечных объемах выборок  разница между свойствами этих оценок все же заметна. В общем случае ОМП по группированным наблюдениям несколько точнее. Исследования конечных выборок оценок параметров сдвига и масштаба, рассматриваемых в данной работе законов, показали, что всегда  и , а при  дисперсионные матрицы оценок практически совпадают. Однако если это преимущество и оказывается за ОМП по группированным наблюдениям, то оно незначительно.

Точность L-оценок в зависимости от числа используемых квантилей. Характер изменения точности L-оценок с ростом числа используемых квантилей при фиксированном объеме выборки  показывают рис. 3.

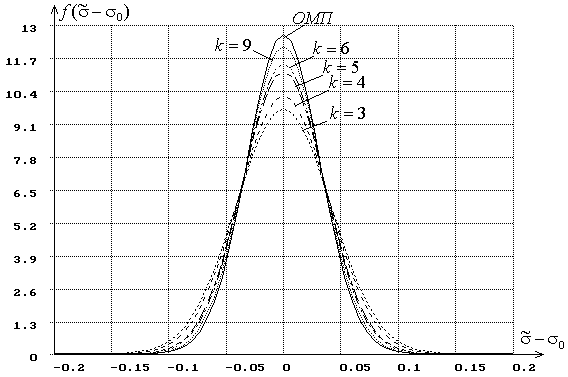
Рис. 3. Плотности распределения L-оценок  при  в зависимости от

На этом рисунке приведены центрированные относительно истинного значения  плотности оценок  параметра нормального закона при объеме выборки  и различном числе  используемых выборочных квантилей для случая одновременного оценивания двух параметров закона. Выборки нормального закона, как и в предыдущем случае, генерировались с параметрами  и . Для сравнения на рисунке представлены центрированное распределение ОМП , полученное также в результате моделирования. Сохраняемое различие в законах распределения ОМП и L-оценок при  связано с величиной относительной асимптотической информации о параметрах закона . Эта величина определяет часть информации, сохраняющейся при группировании выборки (при переходе к выборочным квантилям), и составляющую в данном случае величину 0,8753.

Распределения статистики  Пирсона при использовании L-оценок. При анализе наблюдений случайных величин оценивание параметров модели наблюдаемого закона всегда оказывается лишь первым этапом. Следующим этапом является проверка адекватности построенной модели наблюдаемым данным. Проверка адекватности найденной теоретической модели закона распределения наблюдаемому эмпирическому распределению осуществляется с использованием критериев согласия. Если  мы проверяем согласие по той же выборке, по которой оценивали и параметры, то имеем дело с проверкой сложной гипотезы. В этом случае предельное распределение статистики любого критерия согласия (касается ли это критериев типа  или непараметрических критериев типа Колмогорова и типа Мизеса) зависит от применяемого метода оценивания параметров. И для того, чтобы воспользоваться каким-либо критерием согласия, вычислив L-оценки, необходимо знать (предельное) распределение статистики этого критерия, соответствующее данной проверяемой сложной гипотезе.

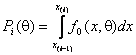В частности, при справедливости сложной проверяемой гипотезы  предельным распределением  статистики критерия согласия Пирсона , где  - объем выборки,  - количество наблюдений, попавших в -й интервал,  - вероятность попадания наблюдения в интервал,  - вектор параметров закона с плотностью , относительно которого проверяется гипотеза, - граничные точки интервалов, является -распределение в том случае, если  компонентов вектора параметров закона оцениваются по этой же выборке в результате минимизации этой же статистики. Статистика  подчиняется -распределению и в том случае, если используются ОМП по группированным наблюдениям (см. стр. 563-567 в [33], стр. 460-470 в [34], [35]). Последнее подтверждают и наши исследования методами статистического моделирования, которые показали хорошее согласие получаемых эмпирических распределений статистики  с -распределениями при проверке сложных гипотез с использованием ОМП по группированным наблюдениям (при конечных объемах выборок).

Начиная исследование распределений статистики  при проверке сложных гипотез с использованием L-оценок, мы надеялись на справедливость наших предположений о том, что и в данном случае предельными распределениями статистики являются -распределения. Действительно, статистическое моделирование распределений статистики  с использованием L-оценок (для различных наблюдаемых законов; при различном числе используемых квантилей, которое соответствует числу интервалов группирования при вычислении статистики; при различном числе оцениваемых параметров) и последующий анализ показали очень хорошее согласие получаемых эмпирических распределений статистики с соответствующими -распределениями.

Например, на рис. 4 представлены эмпирическая функция распределения статистики  при проверке согласия с экспоненциальным законом распределения в случае использования L-оценок масштабного параметра этого закона при объеме выборок  и числе интервалов  и функция -распределения (). Эмпирическая функция распределения построена по выборке из  смоделированных значений статистики .

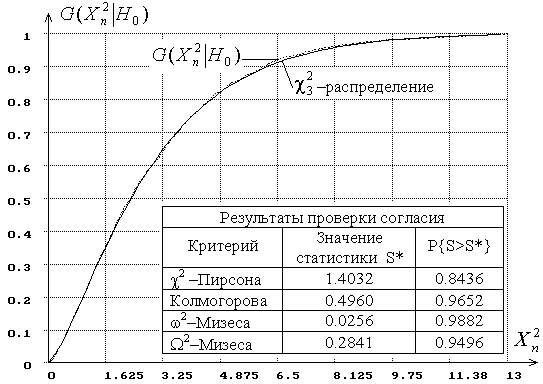
Рис. 4. Распределение статистики  с использованием L-оценок параметра

экспоненциального распределения: , ,

Как видно на приводимом рисунке, эмпирическая функция распределения статистики визуально практически совпадает с теоретическими -распределением. Проверка гипотезы о согласии эмпирического распределения статистики с -распределениями по критериям, реализованным в [36] [ Пирсона, отношения правдоподобия, Колмогорова,  и Мизеса (соответственно, Смирнова-Мизеса и Андерсона-Дарлинга)], подтверждает очень хорошее согласие. Подчеркнем, что в данном случае речь идет о проверке простой гипотезы. На рисунке приведены достигнутые уровни значимости  по каждому из критериев, где  – полученное по выборке значение статистики соответствующего критерия. При проверке согласия по критерию  Пирсона было выбрано 5 интервалов равной вероятности. Как видим, достигнутые уровни значимости по всем критериям очень высоки. Моделирование распределений статистики  при проверке сложных гипотез о согласии с другими законами случайных величин, упоминаемыми в данной работе, при использовании L-оценок параметров сдвига и масштаба показало, что они всегда очень хорошо согласуются с -распределениями. Анализ результатов исследований (при различных законах случайных величин, различных , , ) показал, что нет оснований для отклонения гипотезы о принадлежности распределения статистики  к -распределениям, если при проверке сложных гипотез используются L-оценки по выборочным квантилям.

Вообще говоря, на основании результатов статистического моделирования, если задаться такой целью, можно с любой точностью показать, что в случае использования L-оценок распределением статистики  является соответствующее -распределение (при конкретном законе наблюдаемой величины, конкретных  и ). -распределения являются частным случаем гамма-распределения с плотностью , в котором параметр формы  и параметр масштаба . Наилучшей параметрической моделью для эмпирических распределений статистики , получаемых в результате моделирования, всегда оказываются гамма-распределения. Моделирование серии выборок статистики, сглаживание каждой полученной выборки значений статистики гамма-распределением и последующее усреднение параметров гамма-распределения по всем выборкам серии позволяет уточнить закон распределения статистики. Например, средние значения параметров гамма-распределения по серии из 10 экспериментов, соответствующих проверке согласия с экспоненциальным законом (, , ), составили: =1,50615; =2,00545 (вместо положенных для -распределения значений параметров 1,5 и 2, соответственно). Следует ожидать, что усреднение по большему числу реализаций приведет нас к -распределению. Естественно, что увеличению точности будет способствовать и увеличение .

Аналогичные приведенному примеру результаты получаются при исследовании распределений статистики  в случае проверки сложных гипотез с использованием L-оценок относительно других законов наблюдаемых случайных величин.

Примечание: Мы исследовали методами статистического моделирования распределения статистики  при проверке сложных гипотез с применением оценок по группированным наблюдениям, вычисляемых минимизацией модифицированной статистики , расстояния Хеллингера и дивергенции Кульбака-Лейблера [33]. Оказалось, что во всех этих случаях нет оснований для отклонения гипотезы о принадлежности распределений статистики  к -распределениям. Перечисленные оценки (при известных отличиях [33]) имеют одинаковые асимптотические свойства с оценками по методу минимума статистики , ОМП по группированным наблюдениям [37] и рассматриваемыми L-оценками [1]. Одинаковые асимптотические свойства оценок также являются доводом в пользу справедливости данной гипотезы.

Моделирование псевдослучайных величин. Важным элементом любой системы статистического моделирования является датчик, генерирующий псевдослучайные числа по равномерному закону. Проверка качества такого датчика является непременным условием его использования. Важно, не только то, чтобы получаемые последовательности при любых объемах выборок хорошо соответствовали равномерному закону, но и то, чтобы они удовлетворяли целям исследований [38]. Всегда хорошей дополнительной проверкой качества датчиков может являться построение в результате моделирования той статистической закономерности, которая является известным достоянием теории. Хорошее совпадение результатов моделирования с теоретическими является косвенным подтверждением качества используемого датчика.

В своих исследованиях мы пользовались встроенным датчиком систем программирования С++, собственными реализациями мультипликативного датчика, описанного в [39], реализациями датчиков, рассмотренных в [40]. Датчики исследовались с использованием программной системы [36] и ее последующих версий [41]. Все эти датчики позволяют получать последовательности, достаточно хорошо подчиняющиеся равномерному закону при различных объемах выборок. Все они удовлетворяют требованиям, позволяющим использовать их с целью исследования статистических закономерностей.

Датчик в С++ обладает хорошими свойствами равномерности, но имеет один недостаток, который следует иметь в виду: в генерируемых выборках, начиная с объемов, примерно, в 1700-1800 наблюдений, начинают появляться повторные значения. Например, в сгенерированной выборке из 2000 наблюдений порядка 50 могут оказаться повторившимися дважды. Реализации датчиков [39, 40] такого недостатка не имеют.

Справедливости ради отметим, что значимого влияния отмеченного недостатка первого датчика на результаты проводимых исследований не замечено: выводы оказываются стабильными при любом удовлетворительном датчике.

Пример построения оценок. Выборка в 200 наблюдений представлена следующим вариационным рядом:

-3,9974	-3,4223	-3,3518	-3,2468	-2,9512	-2,8614	-2,5131	-2,4703	-2,3764	-2,3248
-2,2861	-2,2051	-2,1274	-2,1121	-2,0838	-1,9483	-1,9223	-1,8914	-1,8881	-1,8852
-1,5887	-1,5686	-1,5290	-1,5257	-1,4929	-1,4806	-1,4768	-1,4729	-1,4664	-1,3564
-1,3375	-1,2893	-1,2512	-1,2049	-1,1740	-1,1588	-1,1150	-1,1073	-1,0652	-1,0159
-0,9794	-0,9748	-0,9503	-0,9307	-0,9283	-0,8931	-0,8174	-0,7629	-0,7618	-0,6671
-0,5973	-0,5670	-0,5330	-0,5286	-0,5280	-0,5210	-0,5066	-0,5064	-0,3962	-0,3913
-0,3488	-0,3481	-0,3224	-0,3082	-0,2172	-0,2117	-0,1785	-0,1188	-0,1059	-0,0826
0,0369	0,1151	0,1191	0,1206	0,1247	0,1866	0,2199	0,2750	0,2986	0,3649
0,4088	0,4244	0,4301	0,4643	0,4831	0,4901	0,5307	0,5840	0,6085	0,6268
0,6550	0,6613	0,6718	0,6879	0,7179	0,7194	0,8400	0,8587	0,8688	0,9319
0,9336	1,0087	1,0119	1,0192	1,0344	1,0410	1,0414	1,1076	1,1365	1,1450
1,1866	1,2009	1,2240	1,2395	1,3081	1,3413	1,3523	1,3600	1,3729	1,4650
1,4823	1,4885	1,5101	1,6124	1,6513	1,6823	1,7244	1,7244	1,7304	1,7321
1,7458	1,8288	1,8693	1,9080	1,9563	1,9689	1,9811	2,0209	2,0361	2,0434
2,0463	2,0628	2,1042	2,1247	2,2191	2,3264	2,3522	2,3588	2,3621	2,3760
2,3832	2,3922	2,3946	2,4012	2,4455	2,4535	2,4708	2,5525	2,5860	2,6366
2,6404	2,7468	2,7797	2,7945	2,8180	3,0140	3,0515	3,0643	3,0763	3,0835
3,1301	3,1541	3,2029	3,2392	3,3662	3,4533	3,4705	3,5160	3,5551	3,6222
3,6795	3,8301	3,9971	4,0461	4,1126	4,1293	4,2046	4,2724	4,3496	4,3900
4,6509	4,8979	4,9145	5,0427	5,0430	5,1736	5,4432	5,4817	5,5030	6,3378

В предположении, что выборка принадлежит нормальному закону, найдем оптимальные L–оценки его параметров. Число интервалов выбираем максимально возможным. Учитывая ограничение , стараемся, чтобы, по крайней мере, выполнялось неравенство . По табл. 2 останавливаемся  на числе интервалов =7, так как в этом случае . Разбивая упорядоченную выборку на интервалы пропорционально  при =7, находим граничные точки интервалов (оценки квантилей) как средние значения между наблюдениями, попавшими в смежные интервалы:

=(+)/2=(–3,3518–3,2468)/2=–3,2993;

=(+)/2= (–1,8852–1,5887)/2=–1,73695;

=(+)/2= (–0,3481–,3224)/2=–0,33525;

=(+)/2= (1,9811+2,0209)= 2,001;

=(+)/2= (3,5551+3,6222)= 3,58865;

=(+)/2= (5,1736+5,4432)= 5,3084.

Используя коэффициенты из табл. 3, находим оценку параметра сдвига

=0,04318(+)+0,141936(+)+0,314884(+)»0,8741,

и, используя коэффициенты из табл. 4, – оценку параметра масштаба

=0,095717(–)+0,186279(–)+0,136715(–)»2,1353.

На рис. 5 представлены плотность полученного нормального закона и гистограмма, построенная при асимптотически оптимальном группировании [19, 26–28]. В табл. 9 приведены значения статистик непараметрических критериев согласия типа Колмогорова, типа w² Мизеса (Крамера–Мизеса–Смирнова), типа W² Андерсона–Дарлинга и соответствующие значения вероятностей  (достигаемых уровней значимости) при проверке сложных гипотез о согласии. Значения вероятностей  были вычислены в соответствии с построенными распределениями статистик данных критериев согласия для случая применения L-оценок. Распределения статистик непараметрических критериев согласия в случае применения L-оценок отличаются от распределений статистик при проверке сложных гипотез с использованием ОМП [32] и сдвинуты вправо относительно последних. Поэтому при одних и тех же значениях статистик  величины достигаемых уровней значимости  в случае использования L-оценок всегда будут выше.

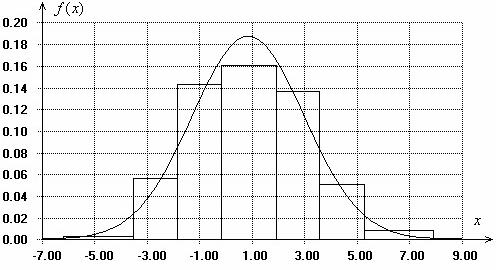
Рис. 5. Гистограмма и плотность нормального закона, построенного

 с использованием L-оценок

Таблица 9

Результаты проверки сложных гипотез о согласии с нормальным законом

Критерий	При =0,8741; =2,1353		При ;
	Значение  статистики		Значение статистики
Типа Колмогорова	0,4506	0,9492	0,6256	0,4611
Типа w^2 Мизеса	0,0296	0,9006	0,0454	0,5838
Типа W^2 Андерсона– Дарлинга	0,2701	0,8004	0,3238	0,5276

Вычисленные по этой же выборке ОМП параметров нормального закона (по негруппированным наблюдениям) равны соответственно , . Результаты проверки согласия также приведены в табл. 9. В данном случае при вычислении вероятностей  использованы распределения статистик из [32]. Как можно заметить, в данном примере в случае L-оценок мы получаем закон, который лучше согласуется с эмпирическим распределением по сравнению со случаем использования ОМП (сравните по значениям статистик соответствующих критериев в табл. 9). Вообще говоря, такая ситуация не типична, но данный пример подчеркивает устойчивость L-оценок к некоторым отклонениям от предполагаемого закона не только на “хвостах”, но и в середине области определения случайной величины. Интересно, что в данном случае при =6 и =5 получаемые L-оценки также оказываются предпочтительнее ОМП в смысле близости эмпирического распределения к соответствующему теоретическому по рассматриваемым критериям согласия.

            Заключение. Предлагаемые вниманию исследователей оптимальные L-оценки параметров сдвига и масштаба по выборочным квантилям являются наилучшими в своем классе.

Применение готовых таблиц вероятностей попадания в интервал, соответствующих асимптотически оптимальному группированию, и формул (1-4), опирающихся на вычисленные таблицы коэффициентов, делает процесс вычисления этих оценок очень простым. Не требуется специального программного обеспечения. Исключая процесс формирования вариационного ряда, который элементарно реализуется сортировкой выборки в любой электронной таблице, все вычисления ограничиваются десятком арифметических операций.

Как и все оценки по группированным данным L-оценки являются робастными. Они устойчивы к наличию аномальных ошибок измерений, к малым отклонениям от исходных предположений о виде наблюдаемого закона распределения. Это позволяет использовать L-оценки в процедурах параметрической отбраковки наблюдений.

L-оценки обладают одинаковыми асимптотическими свойствами с оценками по группированным наблюдениям: максимального правдоподобия; по методу минимума ; модифицированному методу минимума ; получаемых минимизацией расстояния Хеллингера или дивергенции Кульбака-Лейблера [37]. L-оценки выгодно отличаются от перечисленных тем, что в случае L-оценок не требуется реализации итерационного процесса.

Использование L-оценок не вызывает проблем при дальнейшей проверке адекватности полученной модели, так как в данном случае, применяя критерии согласия типа  Пирсона и отношения правдоподобия, в качестве распределений статистик критериев можно воспользоваться -распределениями. Применение готовых таблиц вероятностей попадания в интервал, соответствующих асимптотически оптимальному группированию, с одной стороны, делает элементарной процедуру вычисления статистики , с другой, – обеспечивает максимальную мощность против близких альтернатив.

Полный состав таблиц, которыми можно воспользоваться при вычислении L-оценок и проверке гипотез о согласии, представлен в [28].

Все вышесказанное позволяет рекомендовать использование L-оценок в приложениях, особенно для оперативного анализа данных при контроле технологических процессов. Целесообразность применения L-оценок определяется совокупностью 2-х достоинств: простотой вычислений и робастностью. Естественно, данные рекомендации не исключают возможности применения на последующих этапах анализа более эффективных оценок и более мощных критериев.

ЛИТЕРАТУРА

1. Сархан А.Е., Гринберг Б.Г. Введение в теорию порядковых статистик. – М.: Статистика, 1970. – 414 с.

2. Дэйвид Г. Порядковые статистики.  – М.: Наука, 1979. – 336 с.

3. Егоров В.А., Невзоров В.Б. Асимптотические разложения функции распределения сумм абсолютных порядковых статистик // Вестник ЛГУ, 1975. – № 19. – С. 18-25.

4. Егоров В.А., Невзоров В.Б. Некоторые оценки скорости сходимости сумм порядковых статистик к нормальному закону // Записки научных семинаров ЛОМИ, 1976. – Т. 55.. – С. 165-174.

5. Грибкова Н.В., Егоров В.А. О робастных оценках параметра сдвига, являющихся линейными комбинациями порядковых статистик // Вестник ЛГУ, 1978. – № 13. – С. 24-57.

6. Благовещенский Ю.Н., Самсонова В.П., Дмитриев Е.А. Непараметрические методы в почвенных исследованиях. – М.: Наука, 1987. –  96 с.

7. Бенинг В.Е. Линейные комбинации порядковых статистик: асимптотические свойства и применение в задачах проверки гипотез // Обозрение прикладной и промышленной математики. 1997. – Т.4. – № 3. – С. 497–522.

8. Скрипник В.М., Назин А.Е., Приходько Ю.Г., Благовещенский Ю.Н. Анализ надежности технических систем по цензурированным выборкам. – М.: Радио и связь, 1988. – 183 с.

9. Лемешко Б.Ю. Группирование наблюдений как способ получения робастных оценок // Надежность и контроль качества. – 1997. – № 5. – С. 26-35.

10. Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномальных измерений // Заводская лаборатория. – 1997. – Т.63. – № 5. – С. 43-49.

11. Хьюбер П. Робастность в статистике. – М.: Мир, 1984. – 303 с.

12. Hampel F.R. The influence curve and its role in robust estimation // J. Amer. Statist. Ass., 1974. – V. 69. – № 346. – P. 383-393.

13. Шуленин В.П. Введение в робастную статистику. – Томск: Изд-во Том. ун-та, 1993. – 227 с.

14. Mosteller F. On some useful inefficient statistics. Ann. Math. Statist. 17 (1946). – P. 377-407.

15. Ogawa J. Contributions to the theory of systematic statistics. I. Osaka Math. J. 3 (1951). – P. 175-213.

16. Лемешко Б.Ю. Оптимальные оценки параметров сдвига и масштаба по выборочным квантилям для больших выборок / Тр. третьей международной научно-технической конференциии “Актуальные проблемы электронного приборостроения АПЭП-96”. – Т. 6. – Ч.1. – Новосибирск, 1996. – С. 37-44.

17. Лемешко Б.Ю., Чимитова Е.В. Построение оптимальных L-оценок параметров сдвига и масштаба распределений по выборочным квантилям // Сибирский журнал индустриальной математики. – 2001. – Т.4. – № 2. – С. 166-183.

18. Куллдорф Г. Введение в теорию оценивания по группированным и частично группированным выборкам. – М.: Наука, 1966. – 176 с.

19. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов. В 2-х ч. / Новосиб. гос. техн. ун-т. – Новосибирск, 1993. – 347 с.

20. Eisenberger J., Posner E.C. Systematic statistics used for data compression in space telemetry. J. Amer. Statist. Ass. 60 (1965). - P. 97-133.

21. Saleh A.K.M.J., Ali M.M. Asymptotic optimum quantiles for the estimation of the parameters of the negative exponential distribution. Ann. Math. Statist. 37 (1966). – P. 143-151.

22. Gupta S.S., Gnanadesikan M. Estimation of the parameters of the logistic distribution. Biometrika, 53 (1966). – P. 565-570.

23. Bloch D. A note on the estimation of the location parameter of the Cauchy distribution. J. Amer. Statist. Ass. 61 (1966). – P. 852-855.

24. Hassanein K.M. Analysis of extreme-value data by sample quantiles for very large samples. J. Amer. Statist. Ass. 63 (1968). – P. 877-888.

25. Särndal C.E. Estimation of the parameters of the gamma distribution by sample quantiles. Technometrics. 6 (1964). – P. 405-414.

26. Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть I. Критерии типа  . – Новосибирск: Изд-во НГТУ, 1998. – 126 c.

27. Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат. – М.: Изд-во стандартов. 2002. – 87 с.

28. http://www.ami.nstu.ru/~headrd/.

29. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.583-591.

30. Никулин М.С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.675-676.

31. Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // Заводская лаборатория. 1992. Т. 58. № 3. – С.52-58.

32. Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. - М.: Изд-во стандартов. 2002. - 64 с.

33. Кендалл М., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973. – 900 с.

34. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.

35. Birch M.W. A new proof of the Pearson–Fisher theorem // Ann. Math. Statist. – 1964. V. 35. – P. 817.

36. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. – Новосибирск: Изд-во НГТУ, 1995. – 125 с.

37. Рао. С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968. - 548 с.

38. Ермаков С.М. О датчиках случайных чисел // Заводская лаборатория. – 1993. – Т.59. – № 7. – С. 48-50.

39. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. – М.: Наука, 1982. – 296 с.

40. Рыданова Г.В. Методика изучения временных зависимостей в последовательностях случайных чисел // Заводская лаборатория. – 1986. – Т.52. – № 1. – С. 56-58.

41. Лемешко Б.Ю., Постовалов С.Н. Система статистического анализа наблюдений и исследования статистических закономерностей // Сб. "Моделирование, автоматизация и оптимизация наукоемких технологий". - Новосибирск: Изд-во НГТУ, 2000. - С. 44-46.

---

[1] Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 00-01-00913)

[2] Новосибирский государственный технический университет, г. Новосибирск, Россия