2 Теоретические основы рекомендаций
2.1 Общие положения
Число моделей непрерывных законов распределений, используемых в задачах статистического анализа (при контроле качества, исследованиях надежности и т.д.), немногим превышает 100, а для описания наблюдаемых случайных величин в прикладных исследованиях в основном применяют порядка 30 параметрических законов и семейств распределений.
Это не покрывает многообразия случайных величин, встречаемых на практике. Корректное применение критериев согласия часто приводит (и должно приводить) к отклонению гипотез о принадлежности выборки удобному и привычному закону распределения, например нормальному, так как законы реальных случайных величин, являющиеся следствием многочисленных причин, сложнее тех моделей, которые обычно используют для их описания. Следовательно, и модели должны быть более сложными.
Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой наблюдают. Насколько хорошо наблюдаемая выборка описывается теоретическим законом, проверяют с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию (чаще всего) или необоснованному отклонению проверяемой гипотезы.
Различают простые и сложные гипотезы
о согласии. Простая проверяемая гипотеза имеет вид H0: f(x,q)=f(x,q0), где f(·)– функция
плотности, q0 – известный скалярный или векторный параметр
теоретического распределения, с которым проверяют согласие. Сложная гипотеза
имеет вид H0 : f(x)={f(x,q), q ÎQ}, где Q –
пространство параметров и оценку ![]() скалярного или векторного параметра
вычисляют по той же самой выборке, по которой проверяют гипотезу о согласии.
скалярного или векторного параметра
вычисляют по той же самой выборке, по которой проверяют гипотезу о согласии.
Схема процедуры проверки гипотезы следующая. В
соответствии с применяемым критерием согласия вычисляют значение S*
статистики S как некоторой функции от
выборки и теоретического закона распределения с плотностью f(x,q0) [или ![]() при сложной гипотезе]. Для используемых
на практике критериев асимптотические (предельные) распределения g(S|H0 ) соответствующих статистик при условии истинности
гипотезы H0 обычно
известны. В общем случае для простых и сложных гипотез эти распределения
различаются. Далее в принятой практике статистического анализа обычно полученное
значение статистики S* сравнивают с критическим значением Sa при
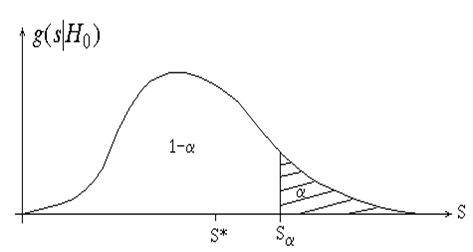
заданном уровне значимости a. Нулевую гипотезу отвергают, если S*>Sa (рисунок 1). Критическое значение Sa, определяемое в случае одномерной статистики из
уравнения
при сложной гипотезе]. Для используемых
на практике критериев асимптотические (предельные) распределения g(S|H0 ) соответствующих статистик при условии истинности
гипотезы H0 обычно
известны. В общем случае для простых и сложных гипотез эти распределения
различаются. Далее в принятой практике статистического анализа обычно полученное
значение статистики S* сравнивают с критическим значением Sa при
заданном уровне значимости a. Нулевую гипотезу отвергают, если S*>Sa (рисунок 1). Критическое значение Sa, определяемое в случае одномерной статистики из
уравнения
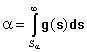 ,
,
обычно берут из соответствующей статистической таблицы или вычисляют.
Рисунок 1 – Плотность распределения статистики при истинной гипотезе H0
Больше информации о степени согласия можно почерпнуть
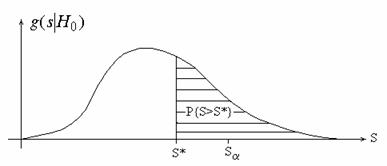
из “достигаемого уровня значимости”: величины вероятности возможного превышения
полученного значения статистики при истинности нулевой гипотезы 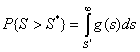 .
Именно эта вероятность позволяет судить о том, насколько хорошо выборка
согласуется с теоретическим распределением, так как по существу представляет
собой вероятность истинности нулевой гипотезы (рисунок 2).
Гипотезу о согласии не отвергают, если P{S>S*}>a.
.
Именно эта вероятность позволяет судить о том, насколько хорошо выборка
согласуется с теоретическим распределением, так как по существу представляет
собой вероятность истинности нулевой гипотезы (рисунок 2).
Гипотезу о согласии не отвергают, если P{S>S*}>a.
Рисунок 2 – Плотность распределения статистики при истинной гипотезе H0
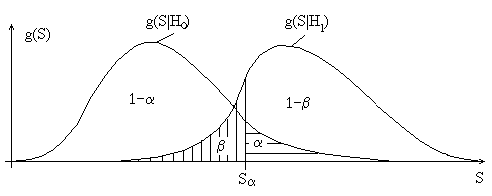
Задачи оценивания параметров и проверки гипотез опираются на выборки независимых случайных величин. Случайность самой выборки предопределяет, что возможны и ошибки в результатах статистических выводов. С результатами проверки гипотез связывают ошибки двух видов: ошибка 1-го рода состоит в том, что отклоняют гипотезу H0, когда она верна; ошибка 2-го рода состоит в том, что принимают гипотезу H0, в то время как справедлива альтернативная (конкурирующая) гипотеза H1. Величина a задает вероятность ошибки 1-го рода. Обычно в критериях согласия не рассматривают конкретную альтернативу, и тогда конкурирующая гипотеза имеет вид H1: f(x,q) ¹f(x,q0). Если гипотеза H1 задана и имеет, например, вид H1: f(x,q) ¹f1(x,q1), то выбор величины a определяет для используемого критерия проверки гипотез и вероятность ошибки 2-го рода b. На рисунке 3 g(S|H0 ) отображает плотность распределения статистики S при истинности гипотезы H0, а g(S|H1) – плотность распределения при справедливости гипотезы H1.
Рисунок 3 – Плотности распределения статистик при справедливости гипотез H0 и H1.
Мощность критерия представляет собой величину 1-b. Очевидно, что чем выше мощность используемого
критерия при заданном значении a, тем лучше он различает гипотезы H0 и H1.
Особенно важно, чтобы используемый критерий хорошо различал близкие альтернативы.
Графически требование максимальной мощности критерия означает, что на рисунке 3 плотности g(S|H0 ) и g(S|H1 ) должны быть максимально “раздвинуты”.
[Предыдущая][Содержание][Следующая]