2.2 Критерии типа c²  при простых гипотезах

Предполагают, что x₁, x_2,…., x_N – выборка значений наблюдаемой случайной величины объема . Процедура проверки гипотез с использованием критериев типа c² предусматривает группирование наблюдений. Область определения случайной величины разбивают на k непересекающихся интервалов граничными точками

x₁<x₂<…<x_k-1< x_k,

где x₀ – нижняя грань области определения случайной величины, x_k – верхняя грань. В соответствии с заданным разбиением подсчитывают число n_i выборочных значений, попавших в i-й интервал, и вероятности попадания в интервал 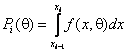, соответствующие теоретическому закону с функцией плотности f(x,q). При проверке простой гипотезы известны как вид функции плотности, так и все параметры закона (известен скалярный или векторный параметр q). При этом , . В основе статистик, используемых в критериях согласия типа c², лежит измерение отклонений n_i /N от P_i(q).

К критериям такого рода, в частности, относят критерий c² Пирсона, критерий отношения правдоподобия [1] и критерии типа c² [2]–[5].

Статистику критерия согласия c² Пирсона вычисляют по формуле

.    (1)

В случае проверки простой гипотезы в пределе при N®¥ эта статистика подчиняется c²_r -распределению с r=k-1 степенями свободы, если верна нулевая гипотеза. Плотность c²_r -распределения описывается формулой

.       (2)

Если верна конкурирующая гипотеза H₁ и выборка соответствует распределению с плотностью f₁(x,q₁) с параметром q₁, то эта же статистика в пределе подчиняется нецентральному c²_r –распределению с тем же числом степеней свободы r=k-1 и параметром нецентральности

,                         (3)

где P_i¹(q₁)– вероятность попадания в интервал при справедливой гипотезе H₁. Плотность нецентрального c²_r –распределения имеет вид [1]

,       (4)

где B(a,b)=G(a)G(b)/G(a+b)– бета-функция.

При заданном уровне значимости a нулевая гипотеза о согласии не должна быть отвергнута, если

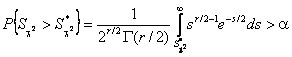,           (5)

где S^*_c² – вычисленное в соответствии с формулой (1) значение статистики.

В критерии отношения правдоподобия использована статистика [1]

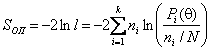,              (6)

которая при верной нулевой гипотезе также асимптотически распределена как c²_r с r=k-1 степенями свободы. Если верна конкурирующая гипотеза H₁ и выборка соответствует распределению с плотностью f₁(x,q₁) и параметром q₁, мерой близости сравниваемых законов является величина

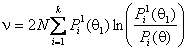.                                 (7)

[Предыдущая][Содержание][Следующая]