2.3 Критерии типа c² при сложных гипотезах

При справедливости H₀ в случае проверки сложной гипотезы и при условии, что оценки параметров находятся в результате минимизации статистики S_c² по этой же самой выборке, статистика S_c² асимптотически распределена как c²_r с числом степеней свободы r=k-m-1, где m – число оцененных параметров. Статистика S_c² имеет это же распределение, если в качестве метода оценивания выбирают метод максимального правдоподобия и оценки вычисляют по сгруппированным данным в результате максимизации по q функции правдоподобия

,                                          (8)

где g – некоторая константа и 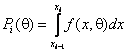 – вероятность попадания наблюдения в i-й интервал значений, зависящая от q.

При вычислении оценок максимального правдоподобия (ОМП) по негруппированным данным эта же статистика распределена как сумма независимых слагаемых , где x₁, x_1,…., x_m – стандартные нормальные случайные величины, независимые одна от другой и от c²_k-m-1, а l₁, l_1,…., l_m – некоторые числа между 0 и 1 [2], [6], [7], представляющие собой корни уравнения

.

В данном уравнении J(q) – информационная матрица Фишера по негруппированным наблюдениям с элементами, определяемыми соотношением

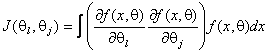,                     (9)

а J_G(q)  – информационная матрица по группированным наблюдениям

.                                     (10)

Функция распределения статистики лежит между c²_k-1– и c²_k-m-1–распределениями. В этом случае, принимая нулевую гипотезу, следует удостовериться, что статистика S_c² не превышает критических значений c²_k-m-1,a и c²_k-1,a, где a – задаваемый уровень значимости. И если c²_k-m-1,a < S^*_c²<c²_k-1,a, то, принимая или отклоняя гипотезу о согласии, можно с одинаковым риском совершить ошибку.

Вышеизложенное относится и к критерию отношения правдоподобия.

Влияние способа группирования на распределения этих статистик при использовании оценок максимального правдоподобия по негруппированным данным – по 2.7.

[Предыдущая][Содержание][Следующая]