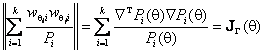2.4 Статистика типа c² Никулина

В работах [2]–[5] предложено видоизменение стандартной статистики S_c², при котором предельное распределение есть обычное c²_k-1 –распределение (число степеней свободы не зависит от числа оцениваемых параметров). Неизвестные параметры распределения F(x,q) в этом случае следует оценивать по негруппированным данным методом максимального правдоподобия. При этом вектор P=(P₁,…,P_k)^T  предполагают заданным, и граничные точки интервалов определяют по соотношениям x_i(q)=F^-1(P₁+…+P_i), . Предложенная статистика имеет вид [3]

Y²_N(q)=Sc²+N^-1a^T(q)L(q)a(q),                              (11)

где S_c² вычислена по формуле (1); матрица , элементы и размерность которой определяются оцениваемыми компонентами вектора параметров q; J(q_i,q_j)– элементы информационной матрицы J(q) по негруппированным данным (9);  – элементы вектора a(q), и

.             (12)

Для распределений, которые полностью определяются только параметрами сдвига и масштаба, справедливо соотношение

                 (13)

и, следовательно,

L(q)=[ J(q) - J_G(q) ]^-1.                                     (14)

Действительно, для законов с параметром сдвига q₁ и масштаба q₂ с функцией распределения F((x-q₁)/q₂)  и плотностью  элементы информационной матрицы  J_G(q) имеют вид:

,

,

,

где t_i=(x_i-q₁)/q₂. Тогда

,

.

Если проверяемая гипотеза H₀ о принадлежности наблюдаемого закона параметрическому семейству f(x,q) неверна, и на самом деле справедлива конкурирующая гипотеза H₁, которой соответствует распределение с плотностью f₁(x,q)= f(x,q)+d(x,q)/, статистика Y²_N(q) в пределе подчиняется нецентральному c²_k-1-распределению с параметром нецентральности [3]

,                          (15)

где 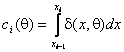,  – элементы вектора d(q), соответствующие оцениваемым компонентам вектора q, а размерность вектора равна числу оцениваемых параметров.

[Предыдущая][Содержание][Следующая]