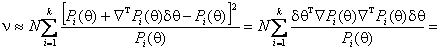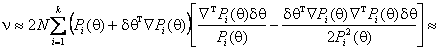2.5 Связь мощности критериев со способом группирования наблюдений

Очевидно, что группирование наблюдений приводит к потере информации, и эти потери зависят от выбора способа группирования данных. Следуя рекомендациям различных литературных источников, на практике обычно строят интервалы равной длины или, в лучшем случае, интервалы равной вероятности. Потери информации о законе распределения в этих ситуациях различны, различна и способность критериев распознавать близкие гипотезы.

Мерой внутренней близости распределений случайных величин служит фишеровская информация, что связано с мощностью различения между близкими значениями параметра. Так как в любой статистике не больше информации, чем в исходной выборке, то мощность различения с помощью статистики не больше, чем с помощью всей выборки. Следовательно, если нужно выбирать между несколькими статистиками, следует предпочесть ту, для которой потери фишеровской информации минимальны [8].

Предполагают, что конкурирующей гипотезе H₁ соответствует распределение того же типа, что и H₀, но с параметром q₁. Можно показать, разлагая P_i(q₁) в соотношении (3) в ряд Тейлора при малых dq=q₁-q и пренебрегая членами высшего порядка, что

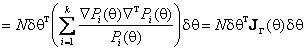,               (16)

где

– информационная матрица Фишера по группированным данным. Мощность критерия c²  Пирсона представляет собой неубывающую функцию от v. Матрица потерь информации, вызванных группированием, DJ=J(q)-J_G(q), где J(q) – информационная матрица Фишера по негрупированным наблюдениям, является неотрицательно определенной, и, следовательно, dq^T DJ dq ³0. Так как dq^T J_G(q) dq=dq^T J(q) dq- dq^T DJ dq, то очевидно, что с ростом потерь информации падает и мощность критерия при близких конкурирующих гипотезах.

Аналогично, с ростом правой части соотношения (7) увеличивается мощность критерия отношения правдоподобия. Действуя как и в предыдущем случае и пренебрегая членами высшего порядка, можно будет иметь

.

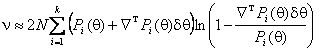Далее, раскладывая ln(1+x) по формуле Тейлора и вновь пренебрегая членами выше 2-го порядка, можно получить

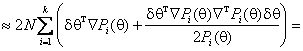
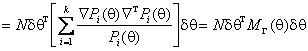.                 (17)

Это соотношение аналогично соотношению (16).

Выражение (14) показывает, что свойства критерия, задаваемого статистикой (11), также зависят от потерь информации при группировании.

[Предыдущая][Содержание][Следующая]