2.7 Характер влияния способов группирования и метода оценивания на распределения статистик типа c²

Вычисленные по конкретной выборке значения статистик типа c² очень сильно зависят от того, как сгруппированы данные. При выборе интервалов группирования одним способом нулевая гипотеза H₀ о согласии может быть отвергнута, другим – принята. При практическом использовании критериев согласия выбирают либо интервалы равной длины, либо интервалы равной вероятности (равной частоты), либо асимптотически оптимальные интервалы [10], [16]–[20]. Использование интервалов равной вероятности было предложено ещё в работе [21]. Разбиение области определения случайной величины (размаха выборки) на интервалы равной длины неоднозначно. Более определенными способами являются равновероятное и асимптотически оптимальное группирования. При асимптотически оптимальном группировании мощность этих критериев для близких альтернатив максимальна [10], [18]–[20].

Для статистики c² Пирсона, вычисляемой в соответствии с формулой (1), при справедливой простой гипотезе H₀ предельное распределение g(S|H₀) есть c²_r –распределение с числом степеней свободы r=k-1. При сложной гипотезе, если по выборке оценивали m параметров закона, статистика подчиняется c²_r –распределению с r=k-m-1 степеней свободы. При справедливой альтернативной гипотезе H₁ предельное распределение g(S|H₁) представляет собой нецентральное c²_r –распределение с тем же числом степеней свободы и параметром нецентральности, определяемым соотношением (3).

В случае проверки сложных гипотез и оценивании по выборке параметров распределений использование в качестве предельных c²_k-m-1–распределений справедливо лишь при определении оценок параметров по сгруппированным данным [1].

Все вышеизложенное относится и к критерию отношения правдоподобия, статистика которого определяется формулой (6).

Выбор способа группирования, в том числе равновероятного или асимптотически оптимального, отражается на предельных распределениях статистик g(S|H₁) (при верной конкурирующей гипотезе). При использовании асимптотически оптимального группирования распределения g(S|H₀) и g(S|H₁) максимально “сдвинуты” относительно друг друга [18]–[20]. Это справедливо как при проверке простых, так и при проверке сложных гипотез.

В случае проверки простых гипотез распределения g(S|H₀) статистик критериев c² Пирсона и отношения правдоподобия при любом разумном способе группирования [равновероятном (РВГ), асимптотически оптимальном (АОГ), равной длины] хорошо согласуются с соответствующим c²_k-1–распределением [22], [23].

При проверке сложных гипотез предельные распределения статистик критериев c² Пирсона и отношения правдоподобия могут зависеть не только от числа оцененных параметров, но и от способа группирования, вида наблюдаемого закона распределения f(x,q), метода оценивания и типа оцениваемого параметра.

В частности, при проверке сложных гипотез и использовании ОМП по негруппированным наблюдениям распределения g(S|H₀) статистик данных критериев существенно зависят от способа группирования.

В работах [22], [23] методами статистического моделирования были проведены исследования законов распределения статистик типа c² при простых и различных сложных гипотезах, при справедливости гипотезы H₀ и справедливости конкурирующей гипотезы H₁, при равновероятном и асимптотически оптимальном группировании.

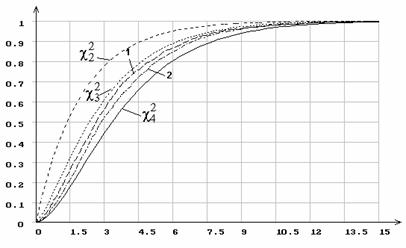
Например, на рисунках 4–7 сопоставлены полученные в результате моделирования эмпирические распределения статистик (при вычислении ОМП по негруппированным наблюдениям) с соответствующими c²_k-m-1–распределениями. Цифрой “1” на указанных рисунках отмечено распределение статистики при асимптотически оптимальном группировании, “2” – при равновероятном группировании. На рисунках 4-6 в качестве примера представлены распределения статистики S_c² при справедливой гипотезе H₀ для пяти интервалов группирования и оценивании по негруппированным данным параметров нормального распределения.

Рисунок 4 – Распределение статистики S_c² при пяти интервалах
группирования и оценивании масштабного параметра
нормального распределения

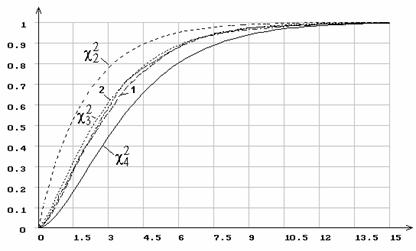
Рисунок 5 – Распределение статистики S_c² при пяти интервалах группирования
и оценивании параметра сдвига нормального распределения

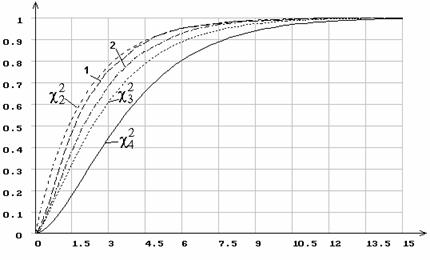
Рисунок 6 – Распределение статистики S_c² при пяти интервалах группирования
и оценивании двух параметров нормального распределения

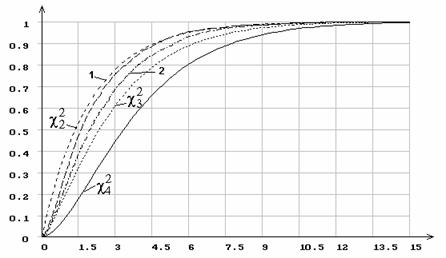
Для сравнения на рисунке 7 представлены распределения статистики S_ОП при пяти интервалах группирования и оценивании обоих параметров нормального распределения при асимптотически оптимальном и равновероятном группировании.

Результаты моделирования и анализа показали [22], [23], что распределения статистик критериев c² Пирсона и отношения правдоподобия при проверке сложных гипотез и вычислении оценок по негруппированным данным существенно отличаются при различных способах группирования. При этом эмпирический закон распределения статистики при асимптотически оптимальном группировании ближе к c²_k-m-1–распределению, чем при равновероятном группировании. Более того, распределения статистик зависят не только от числа оцененных по выборке параметров, но и от того, какой параметр оценивали. Например, оценивание параметра сдвига приводит к более значительному изменению распределения статистики, чем оценивание масштабного параметра. Распределения статистик зависят и от вида наблюдаемого закона. Но эта зависимость не проявляется так резко, как в случае применения для проверки сложных гипотез непараметрических критериев, например типа Колмогорова.

Рисунок 7 – Распределение статистики S_ОП при пяти интервалах группирования и
оценивании  двух параметров нормального распределения

Эмпирические распределения статистики отношения правдоподобия оказываются ближе к c²_k-m-1–распределению, чем соответствующие эмпирические распределения статистики c² Пирсона.

c²_r -распределение с числом степеней свободы r является частным случаем гамма-распределения с основным параметром, равным r/2, и с масштабным – 0,5. Оценивание одного из параметров учитывается уменьшением числа степеней свободы на 1. Так, если измерять изменение предельного закона “в степенях свободы”, то оказывается, что оценивание по негруппированным наблюдениям даже параметра сдвига обычно приводит к изменению “числа степеней” на значение меньшее 1, еще к меньшему изменению в степенях свободы приводит оценивание масштабного параметра. При оценивании по негруппированным наблюдениям двух параметров закона различие между c²_r -распределением и действительным распределением статистики еще более значимо. Таким образом, при вычислении оценок параметров по негруппированным наблюдениям использование в критериях согласия c²_k-m-1–распределения чревато занижением вероятности вида P{S>S^*} и определенным риском отвергнуть верную гипотезу H₀. Занижение P{S>S^*} более существенно при малом числе интервалов группирования. В целом этот риск существенно меньше в случае применения асимптотически оптимального группирования.

Полученные в результате моделирования эмпирические законы распределения статистик рассматриваемых критериев практически всегда с достаточно высокой точностью описываются гамма-распределением.

Использование в критериях согласия c²_k-m-1–распределения для вычисления вероятности вида P{S>S^*} связано с риском отвергнуть верную гипотезу H₀. В случае применения асимптотически оптимального группирования этот риск существенно меньше. В качестве примера в таблице 1 приведены значения вероятностей P{S>S^*} для различных значений статистики S^*, вычисленные по c²₄ –распределению и в соответствии с “действительными” распределениями статистик при семи интервалах группирования и оценивании двух параметров нормального распределения. Эти данные вместе с другими результатами позволяют судить о том, что в случае применения асимптотически оптимального группирования и использования c²_k-m-1–распределения ошибки при вычислении вероятности P{S>S^*} практически незначимы.

Таблица 1 – Значения вероятностей вида P{S>S^*}

Значение S^*	c^24 –распределение	Распределение статистики SОП		Распределение статистики Sc^2
		При АОГ	При РВГ	При АОГ	При РВГ
3	0,5578	0,5876	0,6293	0,5914	0,6304
4	0,4060	0,4303	0,4700	0,4356	0,4716
5	0,2873	0,3049	0,3384	0,3108	0,3403
6	0,1991	0,2108	0,2370	0,2165	0,2389
7	0,1359	0,1430	0,1626	0,1481	0,1643
8	0,0916	0,0956	0,1096	0,0999	0,1111
9	0,0611	0,0632	0,0729	0,0666	0,0741
10	0,0404	0,0413	0,0480	0,0440	0,0489
11	0,0266	0,0268	0,0313	0,0288	0,0320
12	0,0173	0,0173	0,0202	0,0187	0,0207
13	0,0113	0,0110	0,0130	0,0120	0,0133

Исследование распределений статистик при вычислении ОМП по негруппированным данным и дальнейшем увеличении числа интервалов показало возрастающую близость распределений статистик к c²_k-m-1–распределениям. Следовательно, при использовании c²_k-m-1–распределения для вычисления вероятностей вида P{S>S^*} с ростом числа интервалов (при достаточном объеме выборки) ошибки будут снижаться.

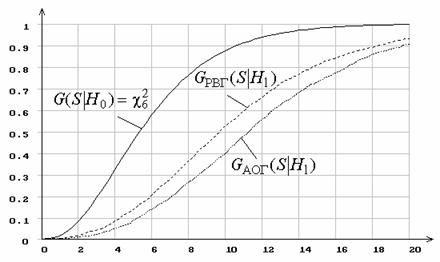
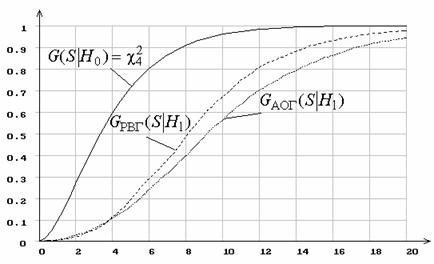
Как отражается способ группирования на предельных распределениях статистики S_c²при справедливости альтернативной гипотезы H₁ показано на рисунках 8–9, где приведены полученные в результате моделирования функции распределения G(S|H₁) при использовании асимптотически оптимального (АОГ) и равновероятного (РВГ) группирования, когда гипотеза H₀ соответствует нормальному закону распределения, а гипотеза H₁ – логистическому. Эти два закона достаточно близки и трудноразличимы с помощью критериев согласия. На рисунке 8 приведены эмпирические распределения статистики при простой гипотезе H₀, а на рисунке 9 – при сложной. Число интервалов группирования – 7. Из рисунков 8, 9 видно, насколько выше мощность критерия при асимптотически оптимальном группировании по сравнению равновероятным.

Рисунок 8 – Распределения статистики S_c² при проверке простой гипотезы H₀

Рисунок 9 – Распределения статистики S_c² при проверке сложной гипотезы H₀

Распределения G(S|H₀) и G(S|H₁) статистики Y²_N(q), определяемой соотношением (11) при использовании оценок максимального правдоподобия параметров по негруппированным данным, несущественно зависят от способа группирования. Исследование этих распределений методами статистического моделирования показало хорошее согласие G(S|H₀) с c²_k-1-распределениями и при равновероятном и при асимптотически оптимальном группировании. При выборе различных способов группирования нет большой разницы между соответствующими распределениями статистики G(S|H₁). При этом критерий оказывается несколько мощнее в случае равновероятного группирования.

Таким образом, по поводу распределений статистик критериев типа c² можно сделать следующие выводы.

Если по наблюдаемой выборке не оценивали параметры закона (простая гипотеза), то распределения статистик типа c² при справедливой гипотезе H₀ достаточно хорошо согласуются с c²_k-1 как при равновероятном, так и при асимптотически оптимальном группировании. Различия между распределениями статистик при равновероятном и асимптотически оптимальном группировании заметны, но незначимы. Распределения статистик при равновероятном группировании в целом оказываются ближе к c²_k-1–распределению.

В условиях, когда оценки параметров определяют по негруппированным наблюдениям, распределения этих статистик хорошо согласуются с гамма-распределениями. При этом:

а) Распределения статистик критериев отношения правдоподобия и c² Пирсона существенно зависят от способа группирования, особенно при малом числе интервалов.

б) Распределения статистик зависят не только от числа оцененных по выборке параметров, но и от того, какой параметр оценивали. В частности, оценивание параметра сдвига приводит к более значительному изменению распределений статистик, чем оценивание масштабного параметра. Картина аналогичная той, что наблюдается для распределений статистик типа Колмогорова, Смирнова и w² Мизеса при проверке сложных гипотез [24].

в) Эмпирические распределения статистики отношения правдоподобия оказываются ближе к предельному теоретическому c²_k-m-1–распределению, чем соответствующие эмпирические распределения статистики c² Пирсона.

г) В целом, при малом числе интервалов и оценивании m параметров число степеней свободы предельного распределения уменьшается на “число степеней свободы” меньшее m. При этом эмпирический закон распределения статистики при асимптотически оптимальном группировании ближе к теоретическому c²_k-m-1–распределению, чем при равновероятном группировании.

д) С ростом числа интервалов k разность между функцией распределения c²_k-m-1 и действительными функциями распределения статистик отношения правдоподобия и c² Пирсона в случае асимптотически оптимального групппирования убывает существенно быстрее.

е) Анализ показал, что при использовании для вычисления вероятностей P{S>S^*} функции распределения c²_k-m-1 при асимптотически оптимальном группировании и малом числе интервалов (k<10) при малых значениях P{S>S^*} (именно при малых вероятностях принимают решение отклонить гипотезу H₀ или нет) погрешность имеет значения, которые не существенны для практических задач. То есть в этом случае, используя c²_k-m-1-распределение, не совершают большой ошибки. В то же время ошибка в определении критического значения S_a может быть достаточно большой. Поэтому целесообразно принимать решение по достигнутому уровню значимости: значению вероятности P{S>S^*}.

ж) С ростом числа интервалов (при соответствующем объеме выборки) отличие распределений статистик S_c² и S_ОП от распределений c²_k-m-1 и при асимптотически оптимальном и при равновероятном группировании становится несущественным.

При справедливости конкурирующей гипотезы H₁ распределения статистик c² и отношения правдоподобия и при простых, и при сложных гипотезах сильно зависят от способа группирования.

Разность G(S|H0)-G(S|H₁) для этих статистик при близких альтернативах в случае использования асимптотически оптимального группирования максимальна, следовательно, максимальна мощность критерия.

Распределения G(S|H₁) статистики Никулина от выбранного способа группирования зависят несущественно.

[Предыдущая][Содержание][Следующая]