3.2 Порядок проверки сложной гипотезы по критериям типа c²

1. При проверке сложной гипотезы и вычислении оценок параметров в результате минимизации соответственно статистик Пирсона

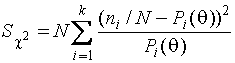
и отношения правдоподобия

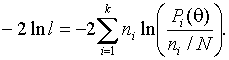
или в результате вычисления по группированным данным оценок максимального правдоподобия или L-оценок порядок проверки аналогичен случаю простой гипотезы с заданием числа степеней свободы r=k-m-1, где m - количество оцененных по данной выборке параметров. При этом остаются в силе рекомендации по способам группирования.

2. При вычислении оценок максимального правдоподобия по исходным негруппированным выборочным данным (по точечной выборке) и использовании для проверки гипотезы статистики Никулина число степеней свободы предельного распределения r=k-1.

3. При вычислении оценок максимального правдоподобия по исходным негруппированным выборочным данным и применении для проверки гипотезы статистик Пирсона или отношения правдоподобия следует руководствоваться следующими соображениями.

3.1. Значения S_r,a процентных точек c²-распределением с числом степеней свободы r=k-m-1 меньше, чем значения процентных точек действительных предельных распределений статистик Пирсона или отношения правдоподобия для такой ситуации. Поэтому, если S*<S_r,a, то гипотеза H₀ о согласии при заданном уровне значимости a заведомо не должна отвергаться.

3.2. Значения процентных точек действительных распределений статистик Пирсона или отношения правдоподобия существенно отличаются от процентных точек c ²-распределением с числом степеней свободы r=k-m-1.

При больших значениях S* вероятности вида P{S>S*}, вычисляемые в соответствии с c²-распределением, достаточно близки к вероятностям P{S>S*}, соответствующим действительным распределениям статистик.

При малых значениях S* вероятности, вычисляемые по формуле

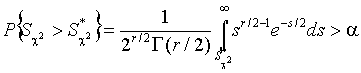
много больше P{S>S*}. Поэтому, если полученная приближенная величина P{S>S*} больше a, то гипотеза о согласии не должна отвергаться.

[Предыдущая][Содержание]