1. СТРУКТУРА ПРЕДСТАВЛЕНИЯ ДАННЫХ, МЕТОДЫ ОЦЕНИВАНИЯ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ОЦЕНОК

1.1.  Структура представления данных

1.2. Виды оценок и методы оценивания

MD–оценки

Метод моментов

Метод минимума  

Модифицированный метод минимума  

Расстояние Хеллингера

Дивергенция Кульбака-Лейблера

Мера расхождения Холдейна

Метод максимального правдоподобия

1.3. Условия существования ОМП по частично группированным данным

1.4. Оценивание параметров распределений по интервальным наблюдениям

 

 

См. также: Прикладная математическая статистика (материалы к семинарам)

 

 

1. СТРУКТУРА ПРЕДСТАВЛЕНИЯ ДАННЫХ, МЕТОДЫ ОЦЕНИВАНИЯ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ОЦЕНОК

 

1.1.  Структура представления данных

 

В данном случае анализируемые наблюдения рассматриваются (в основном) с позиций наиболее общего представления в форме частично груп­пированных выборок. Понятие частично группированной выборки объединяет практически все возможные типы выборок слу­чайных величин. Выборка может быть негруппированной, т.е. состоять только из известных индивидуальных измерений, группированной, когда индивидуальные значения измерений неизвестны, а зафик­сированы лишь границы интервалов и количества наблюдений, попавших в каждый интервал, или частично группированной. В последнем случае часть индивидуальных наблюдений известна, а для других отмечен лишь факт попадания наблюдения в соответствующий интервал значений.

Простейшими случаями частично группированных выборок являются цензурированные выборки, когда имеется один или два крайних интервала группирования.

В частности, большинство измерений, проводимых с помощью различных приборов, представляют собой, вообще говоря, группированные или поразрядно группированные наблюдения, что определяется конечнос­тью цены деления прибора.

Введём определения.

Определение 1. Выборка называется негруппированной, если выбо­роч­ные значения представляют собой индивидуальные значе­ния наблюдений из области определения случайной величины:

,

где N - объем выборки.

Определение 2. Выборка  называется  группированной,  если  область оп­ре­­­деления случайной величины разбита на  непересека­ющихся интервалов граничными точками

,

где  - нижняя грань области определения случайной ве­ли­чины X,  - верхняя грань области определения случайной величины X, и зафиксированы количества наблюдений , попавших в -ый интервал значений. Объем выборки

.

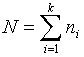Определение 3. Выборка называется частично группированной, если имеющаяся в нашем распоряжении информация связана с множеством непересекающихся интервалов, которые делят область определения случайной величины  так, что каждый интервал принадлежит к одному из двух типов:

а) -ый интервал принадлежит к первому типу, если число  известно, но индивидуальные значения , неизвестны;

б) -ый интервал принадлежит ко второму типу, если  известно не только число , но и все индивидуальные значения .

         В последующем, когда речь будет идти о частично группированной выборке, суммирование по интервалам первого и второго типов будем обозначать соответ­ственно через  и .

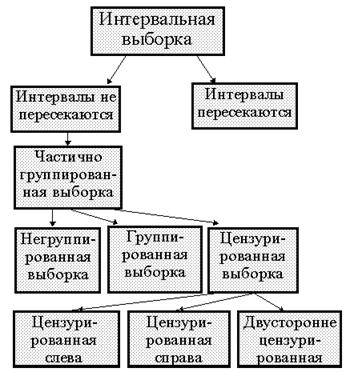
         Дальнейшим обобщени­ем частично группированной выборки является интервальная выборка, в которой каждое наблюдение представлено интервалом , которому принадлежит неизвест­ное точ­но значение . Классификация одномерных выборок показана на рис. 1.1.1. Груп­пиро­ванная выборка задана непересекающимися интервалами, негруп­пи­рованная - вырожденными интервалами, у которых . Интер­­валь­ное представление наблюдения можно интерпретировать как неточное измере­ние случайной величины, связанное либо с заведомо известной погреш­­ностью измеритель­ного прибора, либо с особенностями измеряемой вели­чины. Ин­тер­вальные наблюдения можно получить также в результате обработ­ки измерений, сопровождающихся усечением части данных (напри­мер, при группиро­вании или цензурировании). Приведенная на рис. 1.1.1. классификация не может претендовать на полноту, но охватывает достаточно широкий спектр вариантов регистрации наблюдаемых величин.

         Естественно, что форма представления наблюдений (регистрации) случайных величин отражается на используемых методах и алгоритмах статистического анализа: методах оценивания параметров законов распределения и задачах проверки статистических гипотез.

        

Рис. 1.1.1. Классификация выборочных наблюдений

 

         Понятно, что не только форма представления наблюдений, обычно связанная с технологией их регистрации, влияет на методы обработки, но и методы анализа и свойства используемых статистических процедур иногда определяют преобразование исходных данных. Например, наблюдения груп­пируют при применении критериев согласия  Пирсона и отношения правдоподобия. К группированию можно прибегать с целью получения робастных оценок, как это будет показано в дальнейшем.

 

1.2. Виды оценок и методы оценивания

 

         Среди всего множества различных оценок можно выделить три основных класса оценок [184]. Это M-оценки, L-оценки и R-оценки.

         Пусть  последовательность независимых одинаково распределенных случайных величин с функцией распределения  и функцией плотности .

         В классе M-оценок искомая оценка  определяется как решение задачи вида

,

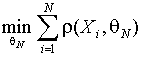или как решение уравнения

.

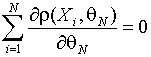К M-оценкам относятся, например, оценки максимального правдоподобия и наименьших квадратов. В случае негруппированных данных для метода максимального правдоподобия .

         L-оценки формируются как линейные комбинации порядковых статистик

,

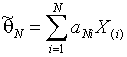где  - i-я порядковая статистика.

         R-оценки, основанные на использовании ранговых критериев, в данном случае мы не рассматриваем.

MD-оценки

          Еще один класс оценок образуют методы минимизирующие расстояния (MD-оценки). Если в пространстве функций распределения для двух функций распределения  и  ввести расстояние , и если случайная величина принадлежит параметрическому семейству с функцией распределения , то MD-оценка определяется выражением

,

где  - эмпирическая функция распределения. Вообще говоря, любая статистика, из используемых в критериях согласия, где различным образом измеряются расстояния между законами распределения, может быть положена в основу метода оценивания. Интерес к MD-оценкам вызывается тем, что они отличаются хорошими робастными свойствами.

         Определяющими факторами при выборе метода оценивания являются структура представления наблюдаемых данных и качество оценок.

          Качество оценок определяется такими свойствами, как состоятельность и асимптотическая эффективность.

Определение 4. Оценка неизвестного параметра  называется состоятельной, если , .

Определение 5. Оценка  называется асимптотически эффективной, если

,

где 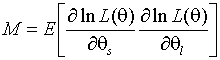 - информационная матрица Фишера;

  векторная случайная величина  при  распределена по нормальному закону с нулевым вектором мате­матического ожидания и ковариационной матрицей, равной .

         Рассмотрим некоторые наиболее часто используемые на практике методы вычисления оценок.

Метод моментов

 Предполагается, что исходная выборка негруп­пирована. Если она группирована, то всем наблюдениям, попавшим в интервал, присваивают значения, равные, например, середине интервала, а затем вычисляют выборочные значения моментов распределения. Пусть первые  моментов распределения существуют и явно выража­ются функциями  ,  неизвест­ных па­ра­­метров, где  - оператор математического ожидания. Выборочные значения моментов вычисляют­ся по формулам

.

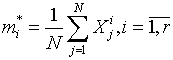Тогда оценки параметров  по методу моментов опреде­ляются как решение системы уравнений

.

         Метод моментов приводит при определённых условиях к состоятельным оценкам. Однако он неприменим, когда теоретические моменты нужного порядка не существуют. Кроме того, эти оценки очень чувствительны к наличию аномальных наблюдений и не всегда эффективны. Если исходная выборка является группированной, то процедура присваивания всем наблюдениям в группе одинаковых значений представляет собой приближение, которое приводит к значительным систематическим ошибкам и требует поправок. Например, если интервалы равны по длине, зачастую используют поправки Шеппарда для моментов, определяемые соотношениями

,

,

,

,

... ,

где  - длина интервала. Введение поправок не всегда приводит к удовлет­ворительным результатам. Иногда оценка, полученная с приме­не­нием поправки, оказывается дальше от истинного значения, чем оцен­ка без поправки. Особенно неудовлетворительные результаты получа­ются, когда мало число групп, т.е. проис­ходит грубое группирование, или область определения случайной величины разбита на интервалы неравной длины.

         Вообще говоря, оценки параметров, получаемые по методу моментов, рационально использовать в качестве начального приближения при поиске оценок более эффективными методами.

        

         Целый ряд методов предполагает использование группированных выборок.

Метод минимума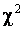

Здесь предполагается, что выборка, по которой оцениваются параметры, полностью группирована. В данном методе оценка определяется как значение параметра, минимизирующее статистику

,

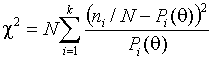где  - вероятность попадания наблюдения в -ый интервал.

Модифицированный метод минимума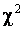

При вычислении оцен­ки мини­мизируется статистика

,

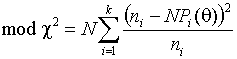где  заменяется на 1, если .

Расстояние Хеллингера

В данном случае при поиске оценки миними­зи­руется статистика

.

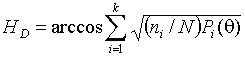Дивергенция Кульбака-Лейблера

Минимизируемая статистика име­ет вид

.

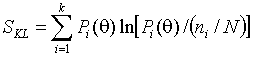Мера расхождения Холдейна

Оценки находятся в результате миними­зации статистики

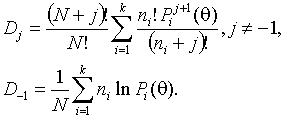
         Все эти методы при соответствующих условиях регулярности, как показал Рао, дают состоятельные и асимптотически эффективные оценки. Однако имеются и различия между этими методами, возникающие при учете введённой Рао эффективности второго порядка [258]. Им показано, что асимптотическая дисперсия оценки определяется соотношением

,

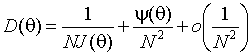где  - информационное количество Фишера о параметре, а вели­чина  определяется методом оценивания и неотрицательна. Если обозначить  для метода максимального правдоподобия, описанного в следующем пункте, как , то для метода минимума  , где  неотрицательная величина, равная нулю только в специальных случаях, для модифицированного  , для расстояния Хеллингера , для диве­ргенции Кульбака-Лейблера , для меры расхождения Холдейна . Следовательно, метод максимального правдоподобия при учёте эффективности второго порядка является наилучшим.

           Кроме того, метод является наиболее универсальным по отноше­нию к форме представления выборочных данных (структуре выборки), по которым оцениваются параметры. Метод моментов требует преобразования группированных данных к негруппированным, только после чего оцениваются параметры с использованием при необходимости (или возможности) поправок на группирование. Напротив, метод мини­мума  и родственные с ним используют только группи­рованные данные: если в распоряжении исследователя имеются индивидуальные наблюдения, выборку следует преобразовывать в полностью группи­рованную. Метод максимального правдоподобия в отличие от других позволяет определять оценки максимального правдоподобия (ОМП) параметров по негруппированным, частично группированным и группи­рованным данным, т.е. дает возможность исследователю самому определять, в каком виде регистрировать и в каком виде хранить экспериментальную информацию в зависимости от харак­теристик приборов, регистрирующих наблюдения, и объема экспериментальной инфор­мации.

Метод максимального правдоподобия

          Оценкой максимального правдоподобия неизвестного параметра по группированным наблюдениям называется такое значение параметра, при котором функция правдоподобия

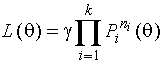,                          (1.2.1)

где  - некоторая константа и 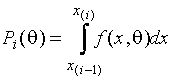 - вероятность попадания на­­блю­дения в -ый  интервал значений, достигает максимума на множестве возможных зна­чений параметра. Здесь предполагается, что для всех  . Для вычисления ОМП дифференцируют функ­цию правдоподобия по  и, приравнивая производные нулю, получают систему уравнений правдоподобия

,

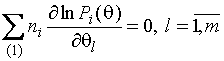где  - размерность вектора параметров .

          Функция правдоподобия для частично группированной выборки имеет вид

,

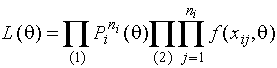система уравнений правдоподобия

,

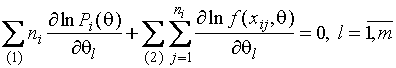где  - функция плотности случайной величины, (1) и (2) означают, что суммирование и умножение осуществляются по интервалам с группированными и негруппированными данными соответственно.

          В случае достаточно больших  при определенных условиях регулярности для функции плотности ОМП существует практически всегда, состоятельна и асимптотически эффективна. Условия существования, асимптотической эффек­тив­ности и состоятельности по группированным и цензурированным выборкам рассматривались в работах Г. Куллдорфа и Н.А. Бодина. Г.Г. Зачепой были получены условия существования ОМП основных параметров распределения Вейбулла и гамма-рас­пре­де­ления. В наших работах получены условия сущест­вования и единственности ОМП для параметров ряда непрерывных законов распределения случайных величин.

          Вообще говоря, метод максимального правдоподобия требует значительного объема вычислений. А в случае группированных или частично группированных данных возникает необходимость в решении задач численного интегрирования, в том числе, и вычисления несобственных интегралов. Именно трудности вычисли­тельного характера, особенно в ситуации группированных и частично группиро­ванных данных, ограничивали использование метода максимального правдоподобия.

          Существует большое число работ, в которых рассматривается вычисление приближенных оценок максимального правдоподобия. В этом случае исходная группированная выборка заменяется негруппированной, в которой индивидуальным значениям присваиваются значения центров интервалов группирования при их равной длине. Далее вычисляются оценки, а затем выводятся выражения для поправок к полученным оценкам.

          Описанные в данном разделе методы вычисления оценок параметров распределений далеко не представляют собой полный перечень всех возможных методов, да эта цель и не преследовалась.

1.3. Условия существования ОМП по частично группированным данным

         При решении уравнений правдоподобия по частично группиро­ван­ным выборкам, особенно по группированным, приходится останавливаться на вопро­сах существования решения уравнения правдоподобия и его единствен­ности. Проверка условий существования и единственности позволяет отказаться от порой трудоемкого и бесполезного процесса вычисления ОМП, если она не существует. При экспериментальных исследованиях, например, надежности, знание условий существования и единственности даёт возможность принять решение о прекращении эксперимента или его продолжении, если по полученным данным нельзя найти оценку параметра  исследуемого распределения.

         Ниже рассматриваются условия существования и единственности ОМП по частично группированным выборкам для скалярных параметров, наиболее часто встречающихся в приложениях одномерных непрерывных распределений.

         Функция плотности распределения Рэлея имеет вид

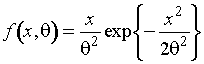                                    (1.3.1)

на множестве , параметр , , .  Веро­ят­ность попадания наблюдения -й интервал

,

где .

Теорема 1.1. ОМП параметра  распределения Рэлея по частично группированной выборке существует при условии

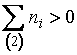 или  и                 (1.3.2)

и получается в качестве единственного решения уравнения правдо­подобия

,

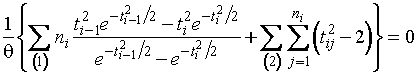где .

         Для доказательства существования достаточно показать, что при условии непрерывности первой и второй производной от логарифма функ­ции правлоподобия первая производная на области определения параметра меняется от некоторого положительного значения до некоторого отрица­тельного. При этом ОМП будет единственна, если для любого , явля­ющегося решением уравнения правдоподобия, вторая производная будет отрицательна.

Доказательство: 1. Покажем, что функции  и  дважды дифференцируемы по :

,

 

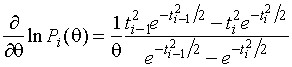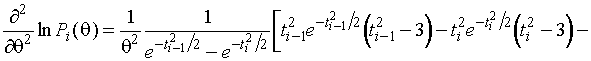
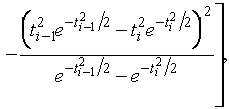                    (1.3.3)

, .

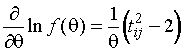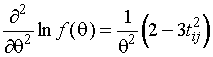2. Так как , то решение уравнения (1.3.2) эквивалентно решению уравнения

 

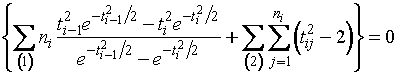.         (1.3.4)

 

         Рассмотрим поведение 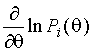 на области определения параметра. Применяя теорему Коши, имеем

,

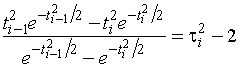где , . Отметим, что при . Отсюда для -го интервала, , принадлежащего первому типу, получаем

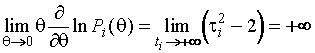.                (1.3.5)

Для , применяя правило Лопиталя,

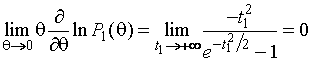.                (1.3.6)

Для

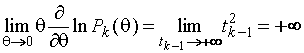.                 (1.3.7)

Для всех интервалов второго типа имеем

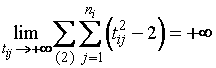.                        (1.3.8)

Из (1.3.5-1.3.8) очевидно, что при условии , если 1-й интервал относится к первому типу, найдется некоторое , для которого выпол­няется неравенство

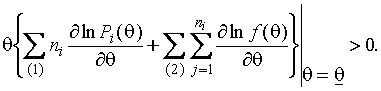            (1.3.9)

Далее при  для -го интервала, , принадлежащего первому типу, имеем

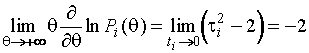.                (1.3.10)

Для , применяя правило Лопиталя,

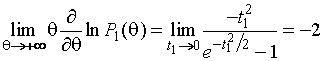.                (1.3.11)

Для

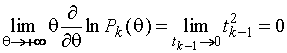.                 (1.3.12)

Для всех интервалов второго типа имеем

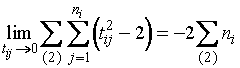.                        (1.3.13)

Из (1.3.10-1.3.13) следует, что при условии , если k-й интервал относится к первому типу, найдется некоторое , для которого выпол­няется неравенство

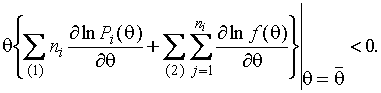            (1.3.14)

Из (1.3.9) и (1.3.14) следует существование ОМП параметра  рас­пределения Рэлея.

         3. Для доказательства единственности ОМП достаточно показать, что

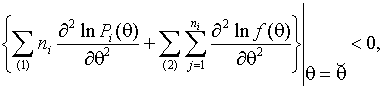            (1.3.15)

где  является решением уравнения правдоподобия (1.3.2).

         Рассмотрим 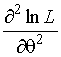. Из (1.3.3) имеем

,

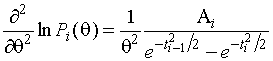где

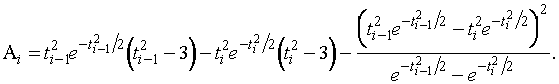
Применяя теорему Коши, получаем для всех

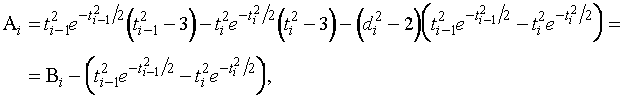
где  и

Далее,

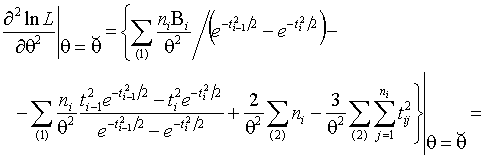
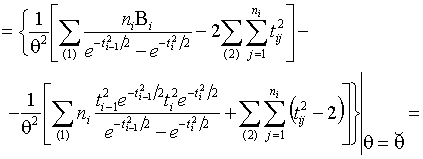
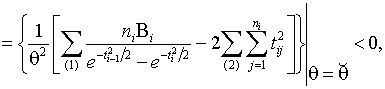
так как .

         Следовательно, ОМП распределения Рэлея по частично группиро­ванной выборке существует и единственна.

         Как следствие этого результата в частном случае справедлива тео­рема для полностью группированной выборки [69]. Для группированной вы­борки  оценка параметра  определяется выражением

.

         При оценивании двух и более параметров распределений методом мак­симального правдоподобия необходимо отыскивать решение системы уравнений правдоподобия, которое доставляет максимум (или локальный максимум) функции правдоподобия. Н.А. Бодиным доказана следующая теорема для группированных выборок [18].

         Теорема 1.21. Пусть для всякого  , для которого , функции  имеют непрерывные первые частные производные на открытой области . Предположим, что сущес­твуют точки  и  области , удов­летворяющие следующим условиям для каждого индекса :

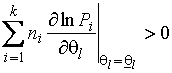;                    (1.3.30)

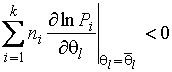                     (1.3.31)

для всех , принадлежащих . Тогда существует ОМП, являющаяся решением системы уравнений правдоподобия, доставляющая локальный максимум функции правдоподобия.

         Справедливость приведенной теоремы сохраняется и для частично группированной выборки. В этом случае добавляется требование сущес­твования первых частных производных функции плотности распределения на области . Условия (1.3.30-1.3.31) преобразуются к виду

,

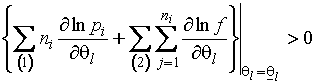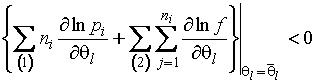
для . Это расширение не нуждается в доказательстве, так как совер­шенно не меняет ход доказательства теоремы 1.21.

         Опираясь на приведенную модификацию теоремы, из анализа полу­ченных выше условий существования ОМП параметров для распределений Вейбулла, нормального, логарифмически нормальных, гамма-распре­деле­ния, распределений экстремальных значений, Коши, логистического, можно утверждать следующее: ОМП векторного параметра перечисленных рас­пределений существует, если 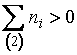 или для  по крайней мере для трех интервалов первого типа . При этом ОМП получается в качестве решения системы уравнений правдоподобия. При попадании на­блю­дений в два крайних интервала первого типа или в какой-то один не крайний существует положительная вероятность отсутствия решения сис­темы уравнений правдоподобия. Естественно, что при попадании всех наблюдений в один из интервалов ОМП не существует.

         Таким образом, получены условия существования и единственности ОМП по частично группированным данным для ряда одномерных непре­рыв­ных рас­пре­делений, наиболее часто используемых на практике при опи­сании реально наблюдаемых случайных величин. Условия сущест­во­ва­ния легко прове­ряемы и в совокупности позволяют предположить сущест­вование ОМП по группированным данным при распределении числа попа­даний наблюдений в число интервалов, большее количества оцениваемых по выборке пара­метров.

 

1.4. Оценивание параметров распределений по интервальным наблюдениям

 

         В случае частично группированной выборки (группированной или негруппированной) одним из наиболее эффективных методов является ме­тод максимального правдоподобия.

         При интервальной выборке наблюдения задаются интервалами, кото­рые в отличие от группированного случая могут пересекаться. Пусть за­дана интервальная вы­борка [83]:

,

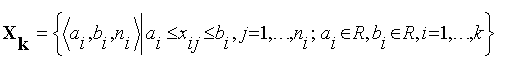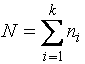где  - число интервалов,  - объём выборки,  - число наблю­де­ний в i-м интервале,  и  - границы i-го интервала,  - точные зна­чения наблю­дений. И пусть

.

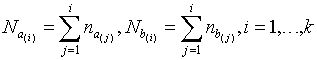         При таком представлении наблюдаемой выборки мы можем пытаться вычислить точечную или интервальную оценку неизвестного параметра распределения. К определению точечной оценки по интервальной выборке пожалуй наиболее естественно адаптируется метод максимального правдо­подобия. Искомая оценка параметра вычисляется как значение , макси­мизирующее выражение

,

 

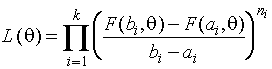где  - функция распределения, параметр которой оценивается по интервальной выборке. Последнее выражение совпадает с выражением (1.2.1) для функции правдоподобия по группированным данным.

         Используя различные статистики, измеряющие расстояния между теоретической функцией распределения и эмпирической, можно строить точечные или ин­тервальные оценки параметров, которые минимизируют эти расстояния (MD-оценки). Эмпирическая функция распределения , построенная по индивидуальным наблю­дениям  (неизвестным нам), будет ограничена снизу и сверху функциями  и , кото­рые имеют следующий вид:

,

.

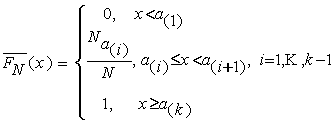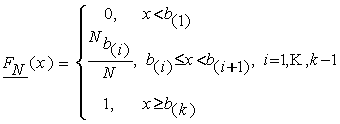То есть,

,  .                        

         Если исследователем априори задана некоторая параметрическая мо­дель , то верхняя и нижняя граница искомой функции распре­деле­ния также должны принадлежать этой модели:

, .

В случае скалярного параметра  мы можем, используя  и , естественным образом получить интервальную оценку параметра, а в случае векторного параметра - оценить область допустимых значений

.

        Так как эмпирическая функция распределения принадлежит некото­рому интервалу неопределенности, то и значение  любой статистики , измеряющей расстояние между эмпирической и истинной функциями рас­пределения также принадлежит соответствующему интервалу , гра­ни­цы которого определя­ют­ся неравенством:

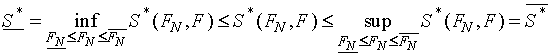
         Если ис­пользовать выражения для оценок сверху и снизу [81-83,98] для статистик, например, применяемых в критериях со­гласия типа Кол­мо­горова, Смирнова,  и  Мизеса, можно постро­ить различные проце­дуры оценивания параметров.

         Из-за неполноты информации об исходных данных, статистические оцен­ки будут зависеть от степени “оптимизма” [63] в отношении согласия модели с наблюдениями случайной величины. Получение точечных оценок параметров рас­пределений является процедурой, в значительной степени зависящей от степени оптимизма исследователя относительно соответствия выбранной модели исходным интервальным данным. Оценку сверху для статистики можно рассматривать как случай наихудшего распо­ложения ин­дивидуальных значений наблюдений в интервалах ("крайний песси­мизм"), а оценку снизу - как случай наилучшего расположения точных значений наблюдений ("крайний оптимизм"). Оценки параметров, соот­ветствующие этим двум крайностям,

,

                                   

можно рассматривать как интервальную оценку неизвестного параметра.

         Заметим, что использование параметрической модели для описания интервальной выборки может оказаться не всегда приемлемым, так как верхняя и нижняя границы эмпирической функции распределения могут сходиться в общем случае к законам из разных параметрических семейств.

         Рассмотренные подходы к оцениванию параметров по интервальной выборке реализуются в разрабатываемом программном обеспечении.

 

[Возврат к вопросам]