Критерии проверки гипотез о средних и
дисперсиях (выдержки из описаний критериев)
Ссылки на результаты
исследований:
Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3.- С.3-15.
Лемешко Б.Ю., Лемешко
С.Б. Об устойчивости
и мощности критериев проверки однородности средних // Измерительная
техника. 2008. № 9. – С.23-28.
Лемешко Б.Ю., Лемешко С.Б., Горбунова А.А.
О применении и
мощности критериев проверки однородности дисперсий. Ч. I. Параметрические критерии //
Измерительная техника. 2010. № 3. – С.10-16.
Лемешко Б.Ю., Лемешко С.Б., Горбунова А.А. О применении и мощности критериев проверки однородности дисперсий. Ч. II. Непараметрические критерии // Измерительная техника. 2010. № 5. – С.11-18.
См. также: Прикладная математическая статистика (материалы к семинарам)
1. Критерии проверки гипотез о математических ожиданиях
1.1. Классические критерии проверки гипотез о математических ожиданиях и дисперсиях по одной выборке
1.2. Сравнение двух выборочных средних из нормальных совокупностей
1.2.0. При известных дисперсиях
1.2.1. При неизвестных, но равных дисперсиях
1.2.2. При неизвестных и неравных дисперсиях
1.3. Сравнение средних значений двух малых выборок по Лорду
1.4. Сравнение средних значений нескольких выборок равного объема по Диксону
1.5. U-критерий Уилкоксона, Манна и Уитни
1.6. H-критерий Краскела-Уаллиса
2. Критерии проверки гипотез о дисперсиях
2.1. Классические критерии проверки гипотез о математических ожиданиях и дисперсиях по одной выборке
2.2. Сравнение двух выборочных дисперсий из нормальных совокупностей
2.3. Проверка равенства нескольких дисперсий для выборок равного объема по Хартли
2.4. Ранговый критерий рассеяния Зигеля и Тьюки
2.5. Упрощенный критерий Тьюки
2.6. Сравнение рассеяния двух малых выборок по Пиллаи и Бунавентуре
2.7. Критерий Левене об однородности дисперсий [Levene, 1960].
1. Критерии проверки гипотез о
математических ожиданиях
1.1. Классические критерии
проверки гипотез о математических ожиданиях и дисперсиях по одной выборке
Пусть мы
имеем выборку ![]() случайных
величин, распределенных по нормальному закону
случайных
величин, распределенных по нормальному закону ![]() . В этом случае
задачи проверки гипотез о математических ожиданиях и дисперсиях формулируются
следующим образом.
. В этом случае
задачи проверки гипотез о математических ожиданиях и дисперсиях формулируются
следующим образом.
1. В
критерии проверки гипотез вида ![]() при известной
дисперсии
при известной
дисперсии ![]() используется
статистика
используется
статистика 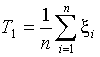 ,
которая при справедливости гипотезы
,
которая при справедливости гипотезы ![]() подчиняется
нормальному распределению:
подчиняется
нормальному распределению: 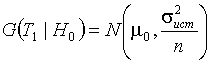 . Проверяемая
гипотеза
. Проверяемая
гипотеза ![]() отклоняется
при больших отклонениях
отклоняется
при больших отклонениях ![]() от
от ![]() .
.
2. Для
проверки гипотезы ![]() при
неизвестной дисперсии
при
неизвестной дисперсии ![]() используется
статистика
используется
статистика 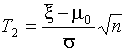 ,
где
,
где 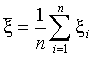 ,
,
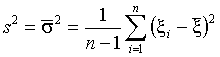 .
При справедливости
.
При справедливости ![]() статистика
статистика
![]() распределена
как
распределена
как ![]() –
распределение Стьюдента.
–
распределение Стьюдента.
1.2. Сравнение
двух выборочных средних из нормальных совокупностей
Проверяется
гипотеза вида ![]() .
.
1.2.0. При известных
дисперсиях
Применение критерия сравнения двух выборочных средних при известных и равных дисперсиях предусматривает вычисление статистики
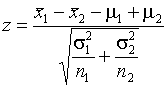 , (5)
, (5)
где
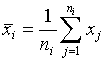 ,
, ![]() - объем
- объем ![]() -й выборки,
-й выборки, ![]()
В случае принадлежности наблюдений нормальным законам
статистика ![]() подчиняется стандартному нормальному закону.
подчиняется стандартному нормальному закону.
1.2.1. При неизвестных, но равных
дисперсиях
При неравных
объемах выборок ![]() статистика
критерия имеет вид
статистика
критерия имеет вид
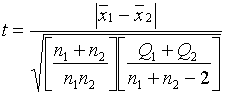 ,
,
где
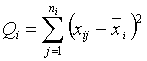 ,
, 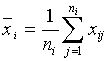 ,
, 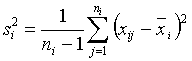 ,
, ![]() , или
, или
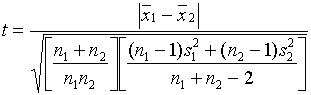 .
.
В случае
нормального закона эта статистика в случае справедливости ![]() должна
подчиняться распределению Стьюдента с числом степеней свободы
должна
подчиняться распределению Стьюдента с числом степеней свободы ![]() , то есть
, то есть ![]() .
.
При равных
объемах выборок ![]() статистика
принимает вид
статистика
принимает вид
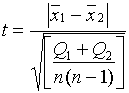 =
=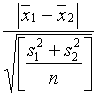 ,
,
а ![]() .
.
1.2.2. При неизвестных и неравных
дисперсиях
Смотри [Закс
Л., с.248-252]. Проверяется гипотеза вида ![]() при условии,
что
при условии,
что ![]() .
Такая задача получила название проблемы Беренса-Фишера
.
Такая задача получила название проблемы Беренса-Фишера
При неравных
объемах выборок ![]() статистика
критерия имеет вид
статистика
критерия имеет вид
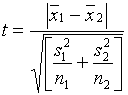 ,
,
а число степеней свободы
 .
.
При равных
объемах выборок ![]() –
–
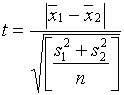
а
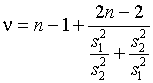 .
.
1.3. Сравнение
средних значений двух малых выборок по Лорду
Смотри [Закс Л., с.254]. [Lord E., 1947]
Критерий предназначен
для сравнения центров независимых рядов измерений равного объема (![]() ). Статистика
критерия имеет вид
). Статистика
критерия имеет вид
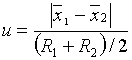 ,
,
где ![]() ,
, ![]() – размахи
выборок. Предполагается принадлежность наблюдений нормальному закону и
равенство дисперсий. Утверждается, что критерий имеет такую же мощность (в
табулированной области объемов выборок), как и t-критерий.
– размахи
выборок. Предполагается принадлежность наблюдений нормальному закону и
равенство дисперсий. Утверждается, что критерий имеет такую же мощность (в
табулированной области объемов выборок), как и t-критерий.
Проверяемая гипотеза отклоняется, когда значение статистики оказывается больше критического.
1.4. Сравнение
средних значений нескольких выборок равного объема по Диксону
Смотри [Закс Л., с.255-256].
[Dixon., 1953]. Критерий
используется для проверки значимости отклонения среднего одной выборки ![]() от
от ![]() средних
значений других выборок. Предполагается, что
средних
значений других выборок. Предполагается, что ![]() является
наименьшим или наибольшим в ряду средних значений
является
наименьшим или наибольшим в ряду средних значений ![]() ,
, ![]() . Ряд средних
значений упорядочивается либо по возрастанию
. Ряд средних
значений упорядочивается либо по возрастанию ![]() , либо по убыванию
, либо по убыванию ![]() . Статистика
критерия имеет вид
. Статистика
критерия имеет вид
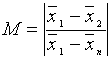 .
.
Проверяемая
гипотеза о незначимости отклонения ![]() от остальных
от остальных ![]() отклоняется
при больших значениях статистики. Рассматриваются варианты данной статистики.
Считается, что критерий устойчив к нарушению предположений о нормальности наблюдаемого
закона.
отклоняется
при больших значениях статистики. Рассматриваются варианты данной статистики.
Считается, что критерий устойчив к нарушению предположений о нормальности наблюдаемого
закона.
1.5. U-критерий
Уилкоксона, Манна и Уитни
Смотри [Закс Л., с.270-281].
Ранговый критерий Манна и Уитни [Mann, Whitney, 1947] основан на критерии Уилкоксона для независимых выборок. Он является непараметрическим аналогом t-критерия для сравнения двух средних значений непрерывных распределений.
Асимптотическая
эффективность U-критерия
равна ![]() по
сравнению с t-критерием
[Закс Л., с.270].
по
сравнению с t-критерием
[Закс Л., с.270].
U-критерий Уилкоксона, Манна
и Уитни проверяет гипотезу о принадлежности двух выборок одной и той же
генеральной совокупности ![]() :
: ![]() . Эта гипотеза
включает также равенство значений медиан
. Эта гипотеза
включает также равенство значений медиан ![]() и равенство
средних значений
и равенство
средних значений ![]() .
.
Для
вычисления статистики упорядочивают ![]() значений
объединенной выборки, определяют сумму рангов
значений
объединенной выборки, определяют сумму рангов ![]() , соответствующую
элементам первой выборки, и сумму рангов второй
, соответствующую
элементам первой выборки, и сумму рангов второй ![]() . Вычисляем
. Вычисляем
![]() ,
,
![]() .
.
Для контроля
правильности можно использовать равенство ![]() . Статистика
критерия имеет вид
. Статистика
критерия имеет вид
![]() .
.
Проверяемая гипотеза отклоняется, когда значение статистики оказывается меньше критического.
Считается, что U-критерий является самым строгим непараметрическим критерием.
Для достаточно больших выборок (![]() ), когда объемы выборок не слишком малы (
), когда объемы выборок не слишком малы (![]() ), используется статистика
), используется статистика
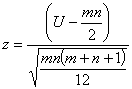 ,
,
хорошо описываемая стандартным нормальным распределением [Mann H.B., Whitney D.R. On a test of whether one of two random variables is stochastically larger than the other // Ann. Math. Statist. 1947. V.18. – p. 50-60].
1.6. H-критерий
Краскела-Уаллиса
Смотри [Закс Л., с.281-283], [Мардиа К., Земроч П., с. 24-27].
Данный
критерий [Kruskal, Wallis, 1952] является
развитием U-критерия
для проверки гипотезы (о равенстве средних) по ![]() выборкам.
выборкам.
Объединенную
выборку 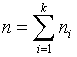 упорядочивают
и вычисляют суммы рангов
упорядочивают
и вычисляют суммы рангов ![]() для
для ![]() -й выборки,
-й выборки, ![]() . Статистика для
проверки нулевой гипотезы имеет вид
. Статистика для
проверки нулевой гипотезы имеет вид
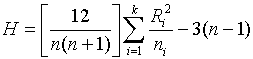 .
.
![]() представляет собой
дисперсию ранговых сумм. При больших
представляет собой
дисперсию ранговых сумм. При больших ![]() и
и ![]() (практически
при
(практически
при ![]() ,
,
![]() )
при справедливости проверяемой гипотезы
)
при справедливости проверяемой гипотезы ![]() статистика
подчиняется
статистика
подчиняется ![]() -распределению.
Проверяемая гипотеза отклоняется при больших значениях статистики.
-распределению.
Проверяемая гипотеза отклоняется при больших значениях статистики.
2. Критерии проверки гипотез о дисперсиях
2.1. Классические
критерии проверки гипотез о математических ожиданиях и дисперсиях по одной
выборке
1. Для
проверки гипотезы вида ![]() при известном
математическом ожидании
при известном
математическом ожидании ![]() вычисляется
статистика
вычисляется
статистика 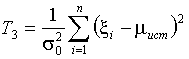 ,
условным распределением которой является
,
условным распределением которой является ![]() – распределение.
– распределение.
2. В
критерии проверки гипотезы вида ![]() при
неизвестном математическом ожидании
при
неизвестном математическом ожидании ![]() используется
статистика
используется
статистика 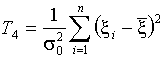 ,
подчиняющаяся
,
подчиняющаяся ![]() – распределению.
– распределению.
2.2. Сравнение
двух выборочных дисперсий из нормальных совокупностей
Для определения того, относятся ли две выборки к одной и той же генеральной совокупности.
Проверяется
гипотеза вида ![]() .
Статистика для проверки гипотезы имеет вид
.
Статистика для проверки гипотезы имеет вид
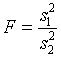 .
.
В случае
принадлежности выборок нормальному закону и справедливости ![]() эта
статистика подчинятся
эта
статистика подчинятся ![]() -распределению
Фишера с числом степеней свободы
-распределению
Фишера с числом степеней свободы ![]() и
и ![]() (
(![]() ). В зависимости от
альтернативы критерий может быть односторонним (
). В зависимости от
альтернативы критерий может быть односторонним (![]() ) или двусторонним
(например,
) или двусторонним
(например, ![]() ).
).
В многочисленных источниках подчеркивается, что результат проверки может сильно зависеть даже от небольших отклонений от нормального распределения.
Непараметрические
критерии о дисперсиях [Cochran,
1947], [Box, 1953], [Box, Anderson, 1955], [Levene, 1960]: для сравниваемых рядов
измерений образуют ![]() и
к ним применяют критерий суммы рангов; если ряды абсолютных отклонений можно
рассматривать как выборки из распределений с равными средними значениями, при
двух выборках применяется U-критерий,
при большем числе выборок H-критерий
Краскела-Уоллиса.
и
к ним применяют критерий суммы рангов; если ряды абсолютных отклонений можно
рассматривать как выборки из распределений с равными средними значениями, при
двух выборках применяется U-критерий,
при большем числе выборок H-критерий
Краскела-Уоллиса.
2.3. Проверка
равенства нескольких дисперсий для выборок равного объема по Хартли
Проверяемая гипотеза о
постоянстве дисперсии ![]() выборок объема
выборок объема ![]() имеет вид:
имеет вид:
![]() .
(1)
.
(1)
а конкурирующая с ней гипотеза –
![]() ,
(2)
,
(2)
где неравенство выполняется,
по крайней мере, для одной пары индексов ![]() ,
, ![]() .
.
Статистика для проверки гипотезы имеет вид
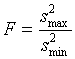 .
.
Степенями свободы для распределения статистики
являются число выборок ![]() и
и ![]() . В [Закс Л.] приводятся таблицы процентных точек для
статистик, заимствованные из [Pearson
E.S., Hartley H.O.]
. В [Закс Л.] приводятся таблицы процентных точек для
статистик, заимствованные из [Pearson
E.S., Hartley H.O.]
2.4. Ранговый
критерий рассеяния Зигеля и Тьюки
Зигель и
Тьюки [Siegel, Tukey, 1960] предложили
непараметрический критерий, основанный на критерии Уилкоксона. Проверяемая
гипотеза ![]() заключается
в том, что две независимые выборки принадлежат к общей генеральной совокупности
с одинаковыми характеристиками рассеяния.
заключается
в том, что две независимые выборки принадлежат к общей генеральной совокупности
с одинаковыми характеристиками рассеяния.
В [Закс Л., с.264-266] говорится, что в случае возрастания различия между средними значениями двух выборок возрастает вероятность ошибки второго рода для данного критерия. В то же время критерий чувствителен к разнице дисперсий при равных параметрах положения.
При
использовании критерия объединенная выборка объемом ![]() (при
(при ![]() ) упорядочивается
(строится вариационный ряд). Ранги элементам такой выборки присваиваются
следующим образом: наименьшее значение получает ранг 1, два наибольших значения
получают ранги 2 и 3, ранги 4 и 5 получают следующие наименьшие значения, 6 и 7
– следующие наибольшие значения и т.д. Если число наблюдений нечетно, то
среднее наблюдение не получает никакого ранга, если четное – оно получает
наивысший ранг.
) упорядочивается
(строится вариационный ряд). Ранги элементам такой выборки присваиваются
следующим образом: наименьшее значение получает ранг 1, два наибольших значения
получают ранги 2 и 3, ранги 4 и 5 получают следующие наименьшие значения, 6 и 7
– следующие наибольшие значения и т.д. Если число наблюдений нечетно, то
среднее наблюдение не получает никакого ранга, если четное – оно получает
наивысший ранг.
Для каждой
выборки определяют сумму рангов ![]() и
и ![]() . При
. При ![]() проверяемой
гипотезе
проверяемой
гипотезе ![]() соответствует
соотношение
соответствует
соотношение ![]() .
Чем больше отличаются
.
Чем больше отличаются ![]() и
и ![]() , тем больше
выборки отличаются по своим дисперсиям.
, тем больше
выборки отличаются по своим дисперсиям.
Для оценки
разности при малых выборках (![]() ) авторы [Siegel, Tukey, 1960] дают точные критические
значения.
) авторы [Siegel, Tukey, 1960] дают точные критические
значения.
Для не
слишком малых выборок (![]() и
и ![]() или
или ![]() и
и ![]() ) используют
статистику
) используют
статистику
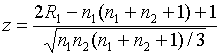 ,
,
где ![]() – сумма
рангов меньшей выборки, которая приближенно подчиняется нормальному закону.
Если
– сумма
рангов меньшей выборки, которая приближенно подчиняется нормальному закону.
Если ![]() ,
то в выражении для статистики
,
то в выражении для статистики ![]() заменяют на
заменяют на ![]() .
.
Следует
иметь ввиду, что при сильно различающихся объемах выборок ![]() и
и ![]() предлагается
использовать скорректированное выражение для статистики:
предлагается
использовать скорректированное выражение для статистики:
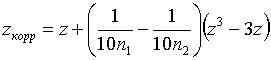 .
.
Другая коррекция для статистики предусматривается в случае присутствия в выборках большого числа одинаковых значений.
2.5. Упрощенный
критерий Тьюки
Смотри [Закс Л., с.266-268].
Не стоит рассматривать.
2.6. Сравнение
рассеяния двух малых выборок по Пиллаи и Бунавентуре
Смотри [Закс Л., с.253].
Предполагается,
что распределения приближенно нормальные. Рассеяния двух независимых выборок
сравниваются по величине размахов. Если ![]() и
и ![]() размахи
выборок с объемами
размахи
выборок с объемами ![]() и
и
![]() и
при этом
и
при этом ![]() >
>![]() , то формируется
статистика
, то формируется
статистика![]() (аналог F-критерия).
В [Pullai, Buenaventura
A.R., 1961] получены верхние
процентные точки для этой статистики при
(аналог F-критерия).
В [Pullai, Buenaventura
A.R., 1961] получены верхние
процентные точки для этой статистики при ![]() и
и ![]() ≤10, которые
приведены в [Закс Л., с.253].
≤10, которые
приведены в [Закс Л., с.253].
2.7. Критерий
Левене об однородности дисперсий [Levene, 1960].
Критерий Левене (Levene 1960) используется
для проверки того, что ![]() выборок имеют равные дисперсии. Критерий Левене
является альтернативой критерию Бартлетта. Считается, что критерий Левене менее
чувствителен к отклонениям от нормальности.
выборок имеют равные дисперсии. Критерий Левене
является альтернативой критерию Бартлетта. Считается, что критерий Левене менее
чувствителен к отклонениям от нормальности.
Проверяемая гипотеза о постоянстве дисперсии ![]() выборок имеет вид:
выборок имеет вид:
![]() .
(1)
.
(1)
а конкурирующая с ней гипотеза –
![]() ,
(2)
,
(2)
где неравенство выполняется,
по крайней мере, для одной пары индексов ![]() ,
, ![]() .
.
Пусть
![]() − объем
− объем ![]() -й выборки,
-й выборки, 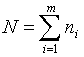 ,
, ![]() −
− ![]() -е наблюдение в
-е наблюдение в ![]() -й выборке. Статистика критерия Левене имеет вид:
-й выборке. Статистика критерия Левене имеет вид:
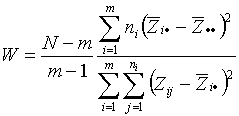 ,
,
где ![]() может определяться одним из следующих способов:
может определяться одним из следующих способов:
1.
![]()
где ![]() − есть среднее в
− есть среднее в ![]() -й выборке.
-й выборке.
2.
![]()
где ![]() − есть медиана в
− есть медиана в ![]() -й выборке.
-й выборке.
3.
![]()
где ![]() − есть усеченное среднее в
− есть усеченное среднее в ![]() -й выборке.
-й выборке.
![]() − есть среднее
− есть среднее ![]() по
по ![]() -й выборке,
-й выборке, ![]() − есть среднее
− есть среднее ![]() по всем выборкам.
по всем выборкам.
Эти три варианта выбора определяют устойчивость критерия Левене. В оригинальной работе Левене предусмотрено только использование выборочных средних. Brown and Forsythe (1974) расширили критерий Левене на случай использования выборочных медиан и усеченного среднего. Их исследования критерия методом Монте-Карло показало, что при использовании усеченного среднего критерий устойчив к отклонениям в сторону распределения Коши, а в случае использования выборочных медиан − к асимметрии закона. Использование среднего обеспечивает лучшую мощность критерия в случае симметричных и умеренно отличающихся распределений.
В критерии Левене проверяемая гипотеза о равенстве дисперсий отклоняется, если
![]() ,
,
где ![]() − верхнее критическое значение
− верхнее критическое значение ![]() -распределения с
-распределения с ![]() и
и ![]() степенями свободы и уровнем значимости
степенями свободы и уровнем значимости ![]() .
.
1.
Levene
H. Robust tests for equality of variances. In I.Olkin and others (Eds):
Contributions to probability and Statistics. Essays in Honor of Harold
Hotelling. Stanford, 1960. – p. 278-292.
2. Brown, M. B. and
Forsythe, A. B. (1974), Journal of the American Statistical Association,
69, 364-367.
Литература
3. Закс Л. Статистическое оценивание. М.: Статистика, 1976. – 598 с.
4.
Cochran
W.G. Some consequences when the assumptions for the analysis or variance are
not satisfied // Biometrics. 1947. V.3. – p. 22-38.
5.
Box
G.E.P. Non-normality and tests on variances // Biometrika. 1953. V. 40. – p.
318-335.
6.
Box
G.E.P., Anderson S.L. Permutation theory in the derivation of robust criteria
and the study of departures from assumption. With discussion // J. Roy.
Statist. Soc., Ser. B. V. 17. 1955. – p. 1-34.
7.
Pearson
E.S., Hartley H.O. Biometrika Tables for Statisticians. Cambridge, 1958. V.1.
8.
Siegel
S., Tukey J.W. A nonparametric sum of ranks procedure for relative spread in
unpaired samples // J. Amer. Statist. Assoc. 1960. V. 55. – p. 429-455.
9.
Mann
H.B., Whitney D.R. On a test of whether one of two random variables is
stochastically larger than the other // Ann. Math. Statist. 1947. V.18. – p.
50-60.
10. Kruskal W.H.,
Wallis W.A. Use of ranks in one-criterion variance analysis // J. Amer.
Statist. Assoc. 1952. V.47. – p. 583-621.
11. Kruskal W.H., Wallis W.A. Use of ranks in one-criterion variance analysis // J. Amer. Statist. Assoc. 1953. V.48. – p. 907-911.
12.
Мардиа К., Земроч П. Таблицы F-распределений и распределений, связанных с ними. М.: Наука, 1984. - 255 с.
13. Lord E. The Use of
the range in place of the standard deviation in the t-test // Biometrika. 1947.
V. 34. – p. 41-67.
14. Dixon W.J.
Processing data for outliers // Biometriks. 1953. V. 9. – p. 74-89.
15. Pullai K.C.S., Buenaventura A.R., Upper percentage points of a substitute F-ratio using ranges // Biometrika. 1961. V. 48. – p. 195-196.