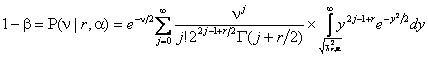2.8 Выбор числа интервалов

Число интервалов группирования, используемое при вычислении оценок параметров, построении гистограмм, вычислении статистик типа отношения правдоподобия или c² Пирсона колеблется в очень широких пределах. Большинство рекомендуемых формул для оценки числа интервалов k носит эмпирический характер и обычно дает завышенные значения.

Определение числа интервалов связано с объемом выборки. Целый ряд рекомендаций из различных источников по выбору числа интервалов k дан в [25].

При выборе интервалов равной длины определяющим является требование, чтобы число наблюдений, попавших в интервалы, было не слишком малым и сравнимым. Такое требование выдвигают в связи с опасением, что в противном случае распределение статистики типа c² не будет являться c²_r –распределением. При этом наиболее часто рекомендуют, чтобы число наблюдений, попавших в интервал, было не менее 10. В [26] отмечено, что на практике допустимо, чтобы число наблюдений в крайних интервалах было менее пяти. В работах [21], [27], посвященных изучению мощности критерия c² Пирсона, в случае унимодального распределения допускается уменьшение ожидаемых частот попадания наблюдений для одного или двух интервалов до 1 и даже ниже. Статистическое моделирование подтверждает, что и в такой ситуации распределения статистик типа c² хорошо согласуются с соответствующими c²_r –распределениями.

Во многих источниках, например в [28], можно найти упоминание эвристической формулы Старджесса для определения “оптимального” числа интервалов

k=log₂ N+1=3,3lgN+1.

В [29] для определения “оптимального” числа интервалов рекомендуют формулу Брукса и Каррузера

k=5lgN

В [30] рекомендуют соотношение

.

В [27] для равновероятных интервалов их число устанавливают порядка

,

где t – квантиль стандартного нормального распределения для заданного уровня значимости. В ряде работ приводят модификации данной формулы. В [31] предлагают значение

k=4lgN,

а в [32] – дальнейшее развитие этого соотношения

k=5lgN-5.

В исследовании [33] получено соотношение

,

где À - значение контрэксцесса ().

При больших объемах выборок N разброс значений k, задаваемых различными формулами, достаточно велик. Поэтому на практике при выборе числа интервалов больше руководствуются тем, чтобы в интервалы попадало число наблюдений не менее 5-10. Так, например, в рекомендациях ВНИИМетрологии [34] в зависимости от  N предлагают следующие значения k:

N	k
40–100	7–9
100–500	8–12
500–1000	10–16
1000–10000	12–22

Все вышеперечисленные рекомендации опирались на предположение, что k следует выбирать таким образом, чтобы вид гистограммы был как можно ближе к плавной кривой плотности распределения генеральной совокупности. В [35] показано, что уклонение гистограммы от плотности распределения в лучшем случае имеет порядок , достигаемый при числе интервалов k порядка .

Очевидно, что “оптимальное” значение k зависит не только от объема выборки, но и от вида закона распределения и от способа группирования.

При асимптотически оптимальном группировании относительно скалярного параметра при 10-11 интервалах в группированной выборке сохраняется около 98% информации, при оптимальном группировании относительно вектора параметров (два параметра) для 15 интервалов – около 95%. Дальнейшее увеличение числа интервалов существенного значения не имеет.

Конкретное число интервалов при асимптотически оптимальном группировании выбирают, исходя из следующих соображений. При оптимальном группировании вероятности попадания в интервалы в общем случае не равны. Обычно минимальны вероятности попадания в крайние интервалы. Поэтому k желательно выбирать из условия NP_i(q) ³5-10 для любого интервала при оптимальном группировании. По крайней мере, минимальная ожидаемая частота должна быть больше 1. В случае использования равновероятного группирования порядок k должен быть примерно таким же, как и при асимптотически оптимальном группировании.

Все наиболее разумные рекомендации по выбору числа интервалов, в том числе по выбору числа интервалов в случае асимптотически оптимального группирования, исходят из того, чтобы при данном N приблизить плотность распределения ее непараметрической оценкой (гистограммой) как можно лучше. Но ни одни из рекомендаций, за исключением [21], [27], не подходят к выбору k с позиций мощности критерия согласия! Не опираются на требование построения наиболее мощного критерия при близких конкурирующих гипотезах.

Хотя известно, что при заданном объеме выборки, заданных конкурирующих гипотезах H₀ и H₁, выбранном способе группирования и фиксированном уровне значимости a с ростом числа интервалов k мощность критериев c² Пирсона и отношения правдоподобия падает [36], [37].

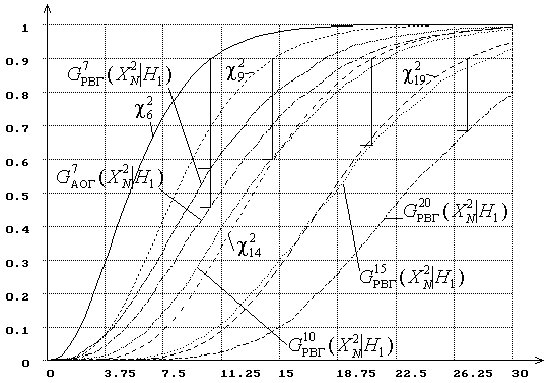
Об изменении мощности критерия c² Пирсона с ростом числа интервалов при проверке простой гипотезы можно судить по рисунку 10. Через X²_N обозначена статистика, вычисляемая в соответствии с формулой (1). На рисунке 10 представлены полученные экспериментально распределения статистики G^k(X²_N|H₀) и G^k(X²_N|H₁) при числе интервалов k=7,10,15,20 и объеме выборки N=500, когда гипотеза H₀ соответствует нормальному закону, а H₁ – логистическому (два очень близких закона). Для k=7  на рисунке приведены распределения при равновероятном G⁷_РВГ(X²_N|H₁) и асимптотически оптимальном G⁷_АОГ(X²_N|H₁)  группировании. Ордината нижнего конца соответствующей вертикальной черты определяет значение b (вероятность ошибки 2-го рода) при уровне значимости a=0,1 для соответствующего числа интервалов. Мощность равна 1- b. Как видно, в полном соответствии с результатами работ [36], [37] при увеличении числа интервалов мощность критерия падает.

Рисунок 10 – Распределения статистики X²_N при проверке простой гипотезы

(H₀ – нормальный закон, H₁ – логистический закон, k=7,10,15,20)

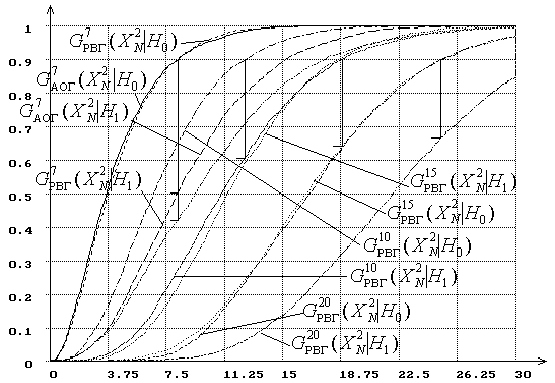
Рисунок 11 – Распределения статистики X²_N при проверке сложной гипотезы 

(H₀ – нормальный закон, H₁ – логистический закон, k=7,10,15,20)

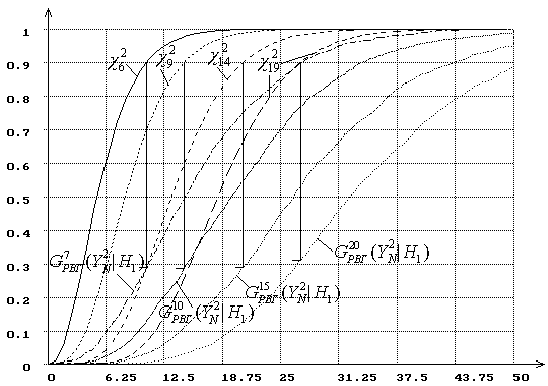
Рисунок 12 – Распределения статистики Y²_N при проверке сложной гипотезы

(H₀ – нормальный закон, H₁ – логистический закон, k=7,10,15,20)

Аналогичные изменения мощности критерия для статистики X²_N в зависимости от числа интервалов при проверке сложной гипотезы иллюстрирует рисунок 11. Здесь также с ростом k мощность критерия падает.

Мощность критерия Никулина с использованием статистики Y²_N с ростом k уменьшается существенно медленней (рисунок 12) и она выше, чем мощность критерия c² Пирсона.

В таблице 2 представлены значения мощности критериев c² Пирсона и типа c² Никулина при рассматриваемой паре альтернатив (H₀ – нормальный закон, H₁ – логистический закон) при различном числе интервалов k в случае простых и сложных гипотез. В колонке 2 приведены значения мощности критерия c² Пирсона при проверке простой гипотезы, полученные по результатам моделирования (экспериментально). В колонке 3 приведены теоретические значения мощности, вычисленные при условии, что G(X²_N|H₀) представляет собой c²_k-1 –распределение, а G(X²_N|H₁) – соответствующее нецентральное распределение. Колонка 4 содержит значения мощности критерия c² Пирсона при проверке сложной гипотезы, полученные по результатам моделирования при использовании ОМП по негруппированным наблюдениям. В колонке 5 приведены теоретические значения мощности критерия c² Пирсона при проверке сложной гипотезы, вычисленные при условии, что G(X²_N|H₀)  представляет собой c²_k-3 -распределение (оценки параметров вычисляют при минимизации статистики X²_N), а G(X²_N|H₁)  – соответствующее нецентральное распределение. В колонке 6 приведены значения мощности критерия Никулина, полученные в результате моделирования распределений статистики Y²_N, а в колонке 7 – расчетные значения мощности этой статистики при рассматриваемой паре гипотез H₀  и H₁.

В таблице 2 приведены значения мощности критериев для k от 6 до 30. Проследив изменение мощности критериев при k <6, можно убедиться, что, если мощность критерия c² Пирсона с уменьшением числа интервалов продолжает возрастать, то мощность критерия Никулина со статистикой Y²_N при k £6  начинает падать. Это свидетельствует о том, что для критерия Никулина существует оптимальное число интервалов, при котором его мощность максимальна.

В [38] мощность критериев типа c² в зависимости от выбираемого числа интервалов k была исследована при различных проверяемых гипотезах H₀ и различных альтернативах H₁ при различных объемах выборок. Величина мощности для критериев типа c² может быть вычислена в соответствии с формулой [39]:

,      (20)

где v – параметр нецентральности, определяемый формулами (3), (7) или (15), c²_r,a – представляет собой (1-a) -процентную точку c²_r -распределения с r степенями свободы (b – заданная вероятность ошибки первого рода, b – вероятность ошибки второго рода). Максимальную мощность критерии c² Пирсона и отношения правдоподобия зачастую имеют или при минимально возможном числе интервалов, определяемом условием r= k-m-1 ³1 , или при оптимальном числе интервалов, близком к минимально возможному. Оптимальное число интервалов для критерия Никулина обычно больше, чем для критериев c² Пирсона и отношения правдоподобия, и не превышает значения .

Таблица 2 – Значения мощности критериев c² Пирсона и типа c² Никулина при уровне значимости a=0,1 (H₀ – нормальный закон, H₁ – логистический закон)

k	В случае простой  Гипотезы		В случае сложной гипотезы
	Для статистики X^2N= Y^2N		Для статистики X^2N		Для статистики Y^2N
	По результатам моделирования	Теоретическая	По результатам моделирования (при использовании ОМП)	Теоретическая (при использовании оценок  minX^2N)	По результатам моделирования	Теоретическая
1	2	3	4	5	6	7
6	0.46	0.449	0.53	0.526	0.70	0.739
7	0.43	0.427	0.49	0.488	0.71	0.750
8	0.42	0.409	0.45	0.459	0.71	0.755
9	0.38	0.395	0.43	0.436	0.71	0.756
10	0.38	0.383	0.43	0.418	0.71	0.756
11	0.37	0.373	0.41	0.403	0.71	0.754
12	0.35	0.364	0.41	0.391	0.70	0.752
13	0.35	0.357	0.38	0.381	0.70	0.749
14	0.34	0.351	0.38	0.373	0.69	0.746
15	0.33	0.345	0.38	0.365	0.69	0.742
16	0.33	0.340	0.38	0.359	0.69	0.738
17	0.32	0.336	0.37	0.353	0.69	0.734
18	0.32	0.332	0.37	0.348	0.69	0.730
19	0.32	0.328	0.35	0.343	0.68	0.726
20	0.31	0.325	0.35	0.339	0.68	0.722
21	0.31	0.322	0.34	0.335	0.67	0.718
22	0.31	0.319	0.34	0.331	0.67	0.714
23	0.31	0.317	0.34	0.328	0.66	0.710
24	0.30	0.314	0.34	0.325	0.66	0.707
25	0.30	0.312	0.34	0.322	0.66	0.703
26	0.30	0.310	0.33	0.320	0.65	0.699
27	0.30	0.308	0.33	0.317	0.65	0.695
28	0.30	0.306	0.32	0.315	0.65	0.692
29	0.30	0.304	0.32	0.313	0.65	0.688
30	0.30	0.302	0.32	0.310	0.65	0.684

Таким образом, выбирая число интервалов в критериях типа c², следует осознавать, что увеличение их числа не приводит к росту мощности критерия. Рекомендуется выбирать число интервалов k так, чтобы для любого интервала при оптимальном группировании выполнялось условие NP_i(q)³5¸10. По крайней мере, минимальная ожидаемая  частота должна быть больше 1. При этом следует опираться на соответствующую таблицу асимптотически оптимального группирования из приложения А. Указания на соответствующую таблицу асимптотически оптимального группирования даны в таблице 3. Снизу значение k ограничено условием k³m+2.

Если заданы конкретная альтернатива и объем выборки N, можно выбрать оптимальное число интервалов k так, чтобы максимизировать соотношение (20).

[Предыдущая][Содержание][Следующая]