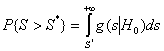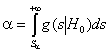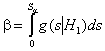2 Общие положения

2.1 Простые и сложные гипотезы при проверке согласия опытного распределения с теоретическим

Применяя критерии согласия для проверки соответствия наблюдаемого опытного распределения теоретическому закону (далее – согласие), следует различать проверку простых и сложных гипотез.

Простая проверяемая гипотеза имеет вид H₀: F(x)=F(x,q), где F(x,q) – функция распределения вероятностей, с которой проверяют согласие наблюдаемой выборки, а q – известное значение параметра (скалярного или векторного).

Сложная проверяемая гипотеза имеет вид H₀: F(x) Î{F(x,q),q ÎQ}, где Q – область определения параметра q. В этом случае оценку параметра распределения  вычисляют по той же самой выборке, по которой проверяют согласие. Если оценку  вычисляют по другой выборке, то гипотеза простая. Далее сложная гипотеза обозначена следующим образом H₀: F(x)=F(x,q), где  – оценка параметра, вычисляемая по этой же выборке.

В процессе проверки согласия по выборке вычисляют значение S^*статистики используемого критерия. Затем для того, чтобы сделать вывод о принятии или отклонении гипотезы H₀, необходимо знать условное распределение G(S|H₀) статистики S при справедливости H₀. И если вероятность

                     (1)

достаточно большая, по крайней мере P{S>S^*}>a, где g(s|H₀) – условная плотность, а a – задаваемый уровень значимости (вероятность ошибки 1-го рода – отклонить справедливую гипотезу H₀), то принято считать, что нет оснований для отклонения гипотезы H₀.

Если в процессе анализа выборки рассматривают некоторую альтернативу H₁: F(x)=F₁(x,q), то с ней связывают условное распределение G(S|H₁)  и вероятность ошибки 2-го рода b (принять гипотезу H₀, в то время как верна гипотеза H₁). Задание значения a для применяемого критерия согласия однозначно определяет и значение b:

,                      (2)

.                                        (3)

При этом, чем больше мощность критерия 1-b, тем лучше он различает соответствующие гипотезы.

[Предыдущая][Содержание][Следующая]