3.1 Порядок проверки простой гипотезы о согласии

Простая проверяемая гипотеза имеет вид H₀: F(x)=F(x,q), где F(x,q) – функция распределения вероятностей, с которой проверяется согласие наблюдаемой выборки, а q – известное значение параметра (скалярного или векторного). В случае простых гипотез предельные распределения статистик критериев согласия Колмогорова, Смирнова, w ² и W ² Мизеса не зависят от вида наблюдаемого закона распределения F(x,q) и, в частности, от его параметров. Говорят, что эти критерии являются “свободными от распределения”. Это достоинство предопределяет широкое использование данных критериев в приложениях.

При проверке согласия опытного распределения с теоретическим распределением случайной величины X действуют в соответствии с пп. 1-4.

1. Формулируют проверяемую гипотезу, выбирая теоретическое распределение случайной величины, согласие которого с опытным распределением этой величины следует проверить.
2. Из совокупности отбирают случайную выборку объема n. Полученные результаты наблюдений располагают в порядке их возрастания, так что в распоряжении имеют упорядоченную выборку значений

x₁ £ x₂ £ … £ x_n.

3. В соответствии с выбранным критерием проверки вычисляют значение статистики S^* критерия [статистику Колмогорова, Смирнова, w² Мизеса или W² Мизеса].
4. В соответствии с выбранным критерием проверки вычисляют значение

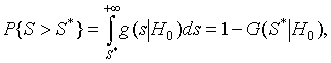
где G(S|H₀) – распределение статистики критерия при справедливости гипотезы H₀. Если P{S>S^*}>a , где a – задаваемый уровень значимости, то нет оснований для отклонения проверяемой гипотезы. В противном случае проверяемая гипотеза H₀ отвергается.

Можно вычисленное значение статистики S^* сравнить с критическим значением S_a , определяемым из условия

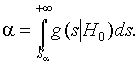
Гипотеза о согласии отвергается, если значение статистики попадает в критическую область, т. е. при S^*> S_a .

[Предыдущая] [Содержание] [Следующая]