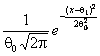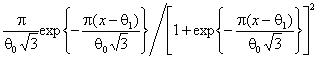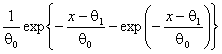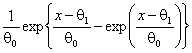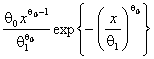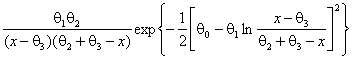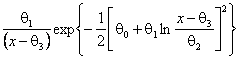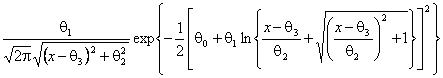3.2.7 Перечень распределений, для которых регламентирована проверка сложных гипотез с использованием настоящих рекомендаций

            Настоящие рекомендации определяют порядок проверки сложных гипотез о согласии с законами распределения, перечень которых приведен в таблице 1.

Таблица 1

Распределение случайной величины	Функция плотности
Экспоненциальное, ³0
Полунормальное, ³0
Рэлея, ³0
Максвелла, ³0
Лапласа,
Нормальное,
Логнормальное,
Коши,
Логистическое,
Наибольшего значения,
Наименьшего значения,
Вейбулла,
Гамма-распределение,
Sb-Джонсона,
Sl-Джонсона,
Su-Джонсона,

            Список распределений, приведенный в таблице 1, достаточно ограничен. Он включает в себя законы распределения, наиболее часто использумые в приложениях в качестве моделей  законов реальных случайных величин. Более широкий набор параметрических моделей законов распределений предложен в справочнике [35]. В случае необходимости проверки сложной гипотезы относительно закона, не вошедшего в представленный перечень, для построения распределения статистики G(S|H₀), соответствующего проверяемой гипотезе H₀, рекомендуется воспользоваться методикой компьютерного анализа, изложенной в 2.3.2.

[Предыдущая] [Содержание] [Следующая]