См. также: Прикладная математическая статистика (материалы
к семинарам)
Доклады СО АН ВШ. Новосибирск, 2000. - № 2. - С. 53-61.
УДК 519.2
МАКСИМИЗАЦИЯ МОЩНОСТИ КРИТЕРИЕВ ТИПА ![]() [1]
[1]
Член-корреспондент СО АН ВШ Б.Ю.
Лемешко,
Е.В. Чимитова
Рассмотрены причины, влияющие на мощность применяемых
критериев согласия типа ![]() .
Показано, что способность критериев различать близкие гипотезы можно повысить
за счет оптимального выбора границ интервалов и числа интервалов.
.
Показано, что способность критериев различать близкие гипотезы можно повысить
за счет оптимального выбора границ интервалов и числа интервалов.
При применении критериев согласия типа ![]() неоднозначность при построении и вычислении
статистик связана с выбором числа интервалов и тем, каким образом область
определения случайной величины разбивается на интервалы. Такой произвол
отражается на статистических свойствах применяемых критериев, в частности, на
их мощности при различении близких конкурирующих гипотез. Очевидно, что выбор
числа интервалов и способа разбиения на интервалы следует осуществлять с
позиций обеспечения максимальной мощности применяемого критерия.
неоднозначность при построении и вычислении
статистик связана с выбором числа интервалов и тем, каким образом область
определения случайной величины разбивается на интервалы. Такой произвол
отражается на статистических свойствах применяемых критериев, в частности, на
их мощности при различении близких конкурирующих гипотез. Очевидно, что выбор
числа интервалов и способа разбиения на интервалы следует осуществлять с
позиций обеспечения максимальной мощности применяемого критерия.
С использованием критериев согласия могут проверяться
простые гипотезы вида ![]() :
:
![]() , где
, где ![]() –
функция распределения вероятностей, с которой проверяется согласие наблюдаемой
выборки независимых одинаково распределенных величин
–
функция распределения вероятностей, с которой проверяется согласие наблюдаемой
выборки независимых одинаково распределенных величин ![]() , а
, а ![]() –
известное значение параметра (скалярного или векторного), и сложные гипотезы
–
известное значение параметра (скалярного или векторного), и сложные гипотезы ![]() :
: ![]() ,
где
,
где ![]() – пространство параметров. В процессе проверки
сложной гипотезы оценка параметра
– пространство параметров. В процессе проверки
сложной гипотезы оценка параметра ![]() вычисляется
по этой же самой выборке.
вычисляется
по этой же самой выборке.
Процедура проверки гипотез о согласии с помощью критериев
типа ![]() предусматривает разбиение области определения
случайной величины на
предусматривает разбиение области определения
случайной величины на ![]() интервалов граничными точками
интервалов граничными точками
![]() .
.
Статистика ![]() Пирсона
вычисляется в соответствии с соотношением
Пирсона
вычисляется в соответствии с соотношением
![]() ,
(1)
,
(1)
где
![]() – количество наблюдений, попавших в
– количество наблюдений, попавших в ![]() -й
интервал,
-й
интервал, 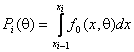 –
вероятность попадания наблюдения в
–
вероятность попадания наблюдения в ![]() -й интервал,
-й интервал, ![]() ,
,
![]() . При справедливой простой гипотезе
. При справедливой простой гипотезе ![]() предельное распределение статистики
предельное распределение статистики ![]() есть
есть ![]() -распределение
с числом степеней свободы
-распределение
с числом степеней свободы ![]() .
Если по выборке оценивалось
.
Если по выборке оценивалось ![]() параметров
закона в результате минимизации статистики
параметров
закона в результате минимизации статистики ![]() , статистика подчиняется
, статистика подчиняется ![]() -распределению с
-распределению с ![]() степенями
свободы. При справедливой альтернативной гипотезе
степенями
свободы. При справедливой альтернативной гипотезе ![]() предельное распределение
предельное распределение ![]() представляет собой нецентральное
представляет собой нецентральное ![]() -распределение с тем же числом степеней свободы и
параметром нецентральности
-распределение с тем же числом степеней свободы и
параметром нецентральности
![]() ,
(2)
,
(2)
где
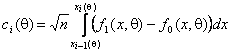 и
и ![]() соответствует
альтернативе.
соответствует
альтернативе.
В случае проверки сложных гипотез и оценивании по выборке параметров
наблюдаемого закона использование в качестве предельных ![]() -распределений
справедливо лишь при определении оценок минимизацией статистики
-распределений
справедливо лишь при определении оценок минимизацией статистики ![]() или при вычислении по
сгруппированным данным оценок максимального правдоподобия (ОМП).
или при вычислении по
сгруппированным данным оценок максимального правдоподобия (ОМП).
Статистика типа ![]() Никулина
[1-4] отличается от
Никулина
[1-4] отличается от ![]() при сложных гипотезах. Предельное распределение
этой статистики – обычное распределение
при сложных гипотезах. Предельное распределение
этой статистики – обычное распределение ![]() (количество
степеней свободы не зависит от числа оцениваемых параметров!). Неизвестные
параметры распределения
(количество
степеней свободы не зависит от числа оцениваемых параметров!). Неизвестные
параметры распределения ![]() в
этом случае должны оцениваться по исходной точечной выборке методом
максимального правдоподобия. Вектор вероятностей попадания в интервал
в
этом случае должны оцениваться по исходной точечной выборке методом
максимального правдоподобия. Вектор вероятностей попадания в интервал ![]() предполагается заданным, и границы интервалов
определяются выражениями
предполагается заданным, и границы интервалов
определяются выражениями ![]() ,
,
![]() .
.
Данная статистика имеет вид [1]
![]() ,
(3)
,
(3)
где
![]() вычисляется в соответствии с (1). Элементы и размерность
матрицы
вычисляется в соответствии с (1). Элементы и размерность
матрицы
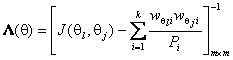
определяются
оцениваемыми компонентами вектора параметров ![]() ,
, ![]() -
элементы информационной матрицы
-
элементы информационной матрицы ![]()
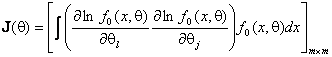 ,
,
![]() -
элементы вектора
-
элементы вектора ![]() ,
величины
,
величины ![]() определяются
соотношением
определяются
соотношением
![]() .
.
При справедливости конкурирующей гипотезы статистика ![]() имеет в качестве предельного
имеет в качестве предельного ![]() нецентральное
нецентральное ![]() -распределение с параметром нецентральности
-распределение с параметром нецентральности
![]() ,
(4)
,
(4)
где
элементы вектора ![]() определяются
соотношением
определяются
соотношением ![]() .
.
Зависимость мощности от способа группирования. Целенаправленно
воздействовать на мощность критериев типа ![]() можно за счет двух
факторов: выбора граничных точек и выбора числа интервалов.
можно за счет двух
факторов: выбора граничных точек и выбора числа интервалов.
Способ группирования особенно сильное влияние оказывает на
предельное распределение ![]() .
В работах [5-9] показано, что критерии согласия
.
В работах [5-9] показано, что критерии согласия ![]() Пирсона и отношения
правдоподобия при проверке как простых, так и сложных гипотез имеют
максимальную мощность против близких альтернатив, если использовать такое
разбиение области определения случайной величины на интервалы, при котором
потери в информации Фишера о параметрах закона, соответствующего гипотезе
Пирсона и отношения
правдоподобия при проверке как простых, так и сложных гипотез имеют
максимальную мощность против близких альтернатив, если использовать такое
разбиение области определения случайной величины на интервалы, при котором
потери в информации Фишера о параметрах закона, соответствующего гипотезе ![]() , минимальны (асимптотически
оптимальное группирование). Чем меньше потери в информации Фишера,
связанные с группированием данных, тем больше параметр нецентральности,
определяемый соотношением (2). В [5,9] для конкретных законов распределения
представлен достаточно широкий состав построенных таблиц асимптотически
оптимального группирования (АОГ-группирования), минимизирующего потери в информации Фишера. При построении
этих таблиц максимизировался определитель
информационной матрицы Фишера по группированным наблюдениям, которая
определяется соотношением
, минимальны (асимптотически
оптимальное группирование). Чем меньше потери в информации Фишера,
связанные с группированием данных, тем больше параметр нецентральности,
определяемый соотношением (2). В [5,9] для конкретных законов распределения
представлен достаточно широкий состав построенных таблиц асимптотически
оптимального группирования (АОГ-группирования), минимизирующего потери в информации Фишера. При построении
этих таблиц максимизировался определитель
информационной матрицы Фишера по группированным наблюдениям, которая
определяется соотношением
![]() .
.
Использование АОГ-группирования при заданном числе интервалов обеспечивает максимальную мощность при близких гипотезах.
Исследование распределений статистики ![]() Никулина, которая
отличается от
Никулина, которая
отличается от ![]() только при сложных гипотезах, показало, что как
только при сложных гипотезах, показало, что как ![]() , так и
, так и ![]() несущественно зависят
от способа группирования. Более того, наши исследования методами
статистического моделирования показали, что с позиций наибольшей мощности
разбиение на интервалы равной вероятности (РВГ-группирование)
оказывается наиболее предпочтительным. Подчеркнем, что критерий типа
несущественно зависят
от способа группирования. Более того, наши исследования методами
статистического моделирования показали, что с позиций наибольшей мощности
разбиение на интервалы равной вероятности (РВГ-группирование)
оказывается наиболее предпочтительным. Подчеркнем, что критерий типа ![]() Никулина мощнее, чем
критерии
Никулина мощнее, чем
критерии ![]() Пирсона
и отношения правдоподобия.
Пирсона
и отношения правдоподобия.
Зависимость мощности от числа интервалов ![]() . Зная предельные
распределения
. Зная предельные
распределения ![]() и
и
![]() статистики
статистики ![]() ,
для любого заданного уровня значимости
,
для любого заданного уровня значимости ![]() можно
оценить мощность соответствующего критерия, рассматривая её как функцию от
числа интервалов
можно
оценить мощность соответствующего критерия, рассматривая её как функцию от
числа интервалов ![]() при
заданном объеме выборки
при
заданном объеме выборки ![]() .
Исследование мощности критериев Пирсона и Никулина как функции от
.
Исследование мощности критериев Пирсона и Никулина как функции от ![]() и
и
![]() проводилось аналитически и методами
статистического моделирования. Причем результаты аналитических вычислений полностью
подтверждаются оценками мощности, полученными на основании моделирования.
проводилось аналитически и методами
статистического моделирования. Причем результаты аналитических вычислений полностью
подтверждаются оценками мощности, полученными на основании моделирования.
Величина мощности для критериев типа ![]() может быть вычислена в соответствии с выражением [10]:
может быть вычислена в соответствии с выражением [10]:
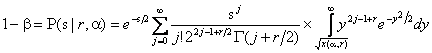 , (5)
, (5)
где
![]() - параметр нецентральности,
определяемый соотношениями (2) и (4),
- параметр нецентральности,
определяемый соотношениями (2) и (4), ![]() представляет
собой
представляет
собой ![]() -процентную
точку
-процентную
точку ![]() -распределения
с
-распределения
с ![]() степенями свободы (
степенями свободы (![]() - заданная вероятность ошибки первого рода,
- заданная вероятность ошибки первого рода, ![]() - вероятность ошибки второго рода). Все
приводимые ниже функции мощности строились при уровне значимости
- вероятность ошибки второго рода). Все
приводимые ниже функции мощности строились при уровне значимости ![]() .
.
На рис. 1 в зависимости от числа ![]() равновероятных интервалов при различных
равновероятных интервалов при различных ![]() представлены функции мощности критерия
представлены функции мощности критерия ![]() Пирсона при проверке простой гипотезы о согласии
с экспоненциальным законом (
Пирсона при проверке простой гипотезы о согласии
с экспоненциальным законом (![]() :
:
![]() при
при ![]() ;
; ![]() :
:
![]() при
при ![]() ).
На рис. 2 приведены аналогичные функции при использовании АОГ-группирования
[5, 9]. И в том, и в другом случае с ростом
).
На рис. 2 приведены аналогичные функции при использовании АОГ-группирования
[5, 9]. И в том, и в другом случае с ростом ![]() мощность
падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
мощность
падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
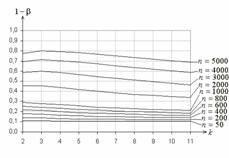
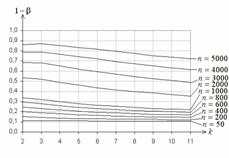
Рис. 1. Рис. 2.
На рис. 3 приведены функции мощности
критерия ![]() Пирсона
в случае РВГ-группирования при проверке простой
гипотезы о согласии с нормальным законом
Пирсона
в случае РВГ-группирования при проверке простой
гипотезы о согласии с нормальным законом ![]() :
:
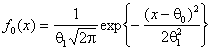 при
при ![]() ,
,
![]() против
против ![]() :
нормальный закон при
:
нормальный закон при ![]() ,
,
![]() . На рис. 4 – аналогичные функции мощности в случае
использования АОГ-группирования [5, 9].
. На рис. 4 – аналогичные функции мощности в случае
использования АОГ-группирования [5, 9].
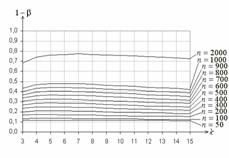
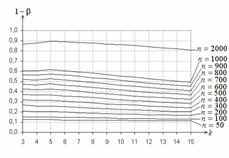
Рис. 3. Рис. 4.
На рис. 5-8 приведены функции мощности критерия ![]() Пирсона при проверке гипотез о согласии с
распределением Вейбулла. На рис.5 представлены
функции мощности критерия
Пирсона при проверке гипотез о согласии с
распределением Вейбулла. На рис.5 представлены
функции мощности критерия ![]() Пирсона
при проверке простой гипотезы о согласии с распределением Вейбулла
при РВГ-группировании. Гипотеза
Пирсона
при проверке простой гипотезы о согласии с распределением Вейбулла
при РВГ-группировании. Гипотеза ![]() :
: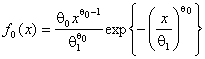 при
при ![]() ,
,
![]() . В качестве альтернативы
. В качестве альтернативы ![]() рассматривается также распределение Вейбулла, но с параметрами
рассматривается также распределение Вейбулла, но с параметрами ![]() ,
, ![]() .
На рис. 6 для этой же пары гипотез приведены функции мощности критерия для АОГ-группирования. На рис. 7 приведены функции мощности
критерия
.
На рис. 6 для этой же пары гипотез приведены функции мощности критерия для АОГ-группирования. На рис. 7 приведены функции мощности
критерия ![]() Пирсона
при проверке сложной гипотезы о согласии с распределением Вейбулла
при использовании РВГ-группирования и близкой
альтернативе, соответствующей распределению Накагами
Пирсона
при проверке сложной гипотезы о согласии с распределением Вейбулла
при использовании РВГ-группирования и близкой
альтернативе, соответствующей распределению Накагами
![]() :
: 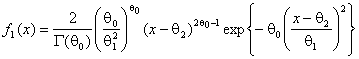
при
![]() ,
, ![]() ,
,
![]() . Рис. 8 иллюстрирует функции мощности для той же пары
гипотез для случая АОГ-группирования.
. Рис. 8 иллюстрирует функции мощности для той же пары
гипотез для случая АОГ-группирования.
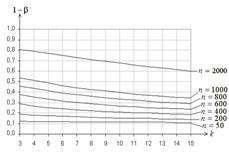
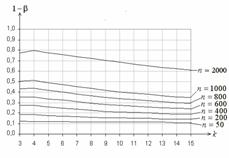
Рис. 5. Рис. 6.
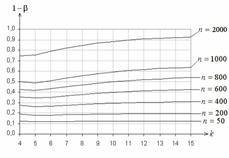
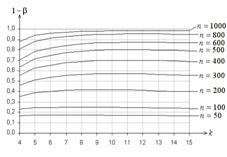
Рис. 7. Рис. 8.
На рис. 9 представлены функции мощности критерия типа ![]() Никулина при проверке сложной гипотезы о
согласии с нормальным законом
Никулина при проверке сложной гипотезы о
согласии с нормальным законом
![]() :
: 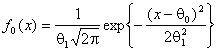 ,
,
когда в качестве альтернативы рассматривается близкий ему логистический закон
![]() :
: 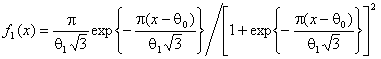
при
значениях параметров ![]() ,
,
![]() . Отметим, что функции мощности критерия
. Отметим, что функции мощности критерия ![]() Пирсона в данной ситуации являются строго
убывающими по
Пирсона в данной ситуации являются строго
убывающими по ![]() функциями и принимают максимальное значение при минимально
возможном значении числа интервалов
функциями и принимают максимальное значение при минимально
возможном значении числа интервалов ![]() .
.
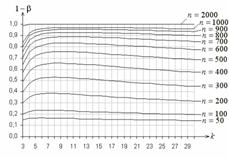
Рис. 9.
Результаты расчета функций мощности по соотношению (5) контролировались
статистическим моделированием функций мощности, при котором строились
эмпирические функции распределений ![]() и
и ![]() для статистик
для статистик ![]() рассматриваемых
критериев, и находились оценки мощности. Результаты моделирования оказались
очень близкими к расчетным.
рассматриваемых
критериев, и находились оценки мощности. Результаты моделирования оказались
очень близкими к расчетным.
Заключение.
Анализ функций мощности для различных альтернатив при проверке простых
и сложных гипотез показывает, что с увеличением числа интервалов мощность
критериев типа ![]() падает.
Это соответствует и результатам работ [11,12]. Максимальная мощность критериев
при заданном объеме выборки
падает.
Это соответствует и результатам работ [11,12]. Максимальная мощность критериев
при заданном объеме выборки ![]() чаще
всего достигается или при минимальном числе интервалов, или при некотором
оптимальном значении
чаще
всего достигается или при минимальном числе интервалов, или при некотором
оптимальном значении ![]() .
.
Максимизировать мощность критериев ![]() Пирсона и отношения
правдоподобия можно за счет оптимального выбора двух факторов: выбора АОГ-группирования в качестве способа
разбиения области определения случайной величины и подбора оптимального
числа интервалов
Пирсона и отношения
правдоподобия можно за счет оптимального выбора двух факторов: выбора АОГ-группирования в качестве способа
разбиения области определения случайной величины и подбора оптимального
числа интервалов ![]() при
заданном объеме выборки
при
заданном объеме выборки ![]() .
Увеличение мощности критерия типа
.
Увеличение мощности критерия типа ![]() Никулина возможно только
за счет выбора оптимального числа интервалов.
Никулина возможно только
за счет выбора оптимального числа интервалов.
Оптимальное число интервалов ![]() зависит от объема
выборки
зависит от объема
выборки ![]() и от
конкретной пары конкурирующих гипотез
и от
конкретной пары конкурирующих гипотез ![]() и
и ![]() . Чаще всего оптимальное
. Чаще всего оптимальное ![]() оказывается существенно
меньше значений, рекомендуемых различными регламентирующими документами и
задаваемых множеством эмпирических формул, широкий перечень которых приводится,
например, в [13].
оказывается существенно
меньше значений, рекомендуемых различными регламентирующими документами и
задаваемых множеством эмпирических формул, широкий перечень которых приводится,
например, в [13].
Рассматривая пару альтернатив, всегда можно выбрать оптимальное число интервалов и подобрать оптимальное разбиение на интервалы. В результате будет получен критерий максимальной мощности, наилучшим образом различающий данные конкурирующие гипотезы.
В случае проверки простых гипотез при оптимальном выборе числа
интервалов и асимптотически оптимальном группировании, минимизирующем
потери в информации Фишера, критерии типа ![]() мощнее непараметрических
критериев типа Колмогорова и типа
мощнее непараметрических
критериев типа Колмогорова и типа ![]() и
и ![]() Мизеса.
А при проверке сложных гипотез в тех же условиях они лишь не многим уступают последним.
Мизеса.
А при проверке сложных гипотез в тех же условиях они лишь не многим уступают последним.
ЛИТЕРАТУРА
[1] Никулин М.С. // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.675-676.
[2] Никулин М.С. // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.583-591.
[3] Мирвалиев М., Никулин
М.С. // Заводская лаборатория. 1992. Т. 58. № 3. – С.52-58.
[4] Aguirre N., Nikulin M. // Kybernetika. 1994. V. 30. № 3. – P.214-222.
[5] Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. – 346 с.
[6] Лемешко Б.Ю. // Надежность и контроль качества. – 1997. – № 8. – С. 3-14.
[7] Лемешко Б.Ю. // Заводская лаборатория, 1998. Т. 64. – №1. – С.56-64.
[8] Лемешко Б.Ю., Постовалов С.Н. // Заводская лаборатория. 1998. Т. 64. – № 5. – С.56-63.
[9] Денисов В.И., Лемешко Б.Ю., Постовалов С.Н.
Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть I.
Критерии типа ![]() .
– Новосибирск: Изд-во НГТУ, 1998. –126 с.
.
– Новосибирск: Изд-во НГТУ, 1998. –126 с.
[10] Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.
[11] Чибисов Д.М., Гванцеладзе Л.Г. // III советско-японский симпозиум по теории вероятностей. Ташкент: изд-во “Фан”, 1975. – С. 183-185.
[12] Боровков А.А. // Теория вероятностей и ее применение. 1977. Т. XXII. № 2. – С.375-378.
[13] Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомиздат, 1991. - 303 с.
[1] Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 00-01-00913)