См. также: Прикладная математическая статистика (материалы
к семинарам)
Доклады СО АН ВШ. 2002. - № 1(5). - С.65-74.
УДК 519.2
НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ ПРИ ПРОВЕРКЕ СЛОЖНЫХ ГИПОТЕЗ О СОГЛАСИИ С РАСПРЕДЕЛЕНИЯМИ ДЖОНСОНА[1]
Член-корреспондент
САН ВШ Б.Ю. Лемешко,
С.Н.
Постовалов
Методами статистического моделирования построены распределения статистик непараметрических критериев при проверке сложных гипотез о согласии с распределениями Джонсона.
Одной из наиболее распространенных задач
статистического анализа при обработке результатов экспериментальных наблюдений
является проверка согласия полученного опытного распределения с теоретическим.
Применяя критерии согласия, различают проверку простых и сложных гипотез.
Простая проверяемая гипотеза имеет вид 
:
, где 
–
функция распределения вероятностей, с которой проверяется согласие
наблюдаемой выборки, а 
–
известное значение параметра (скалярного или векторного). При проверке сложной
гипотезы проверяемая гипотеза имеет вид :
, где 
–
область возможных значений параметра. В этом случае оценка параметра распределения
вычисляется по той же самой выборке, по которой
проверяется согласие.
В процессе проверки согласия по выборке вычисляется
значение 
статистики
используемого критерия. Затем для того, чтобы сделать вывод о том, принять или
отклонить гипотезу ,
необходимо знать условное распределение 
статистики
при справедливости 
. И если вероятность
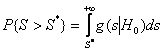
достаточно большая, по крайней мере 
, где 
– условная плотность, а 
– задаваемый уровень значимости (вероятность
ошибки первого рода – отклонить справедливую гипотезу ), то принято считать, что нет оснований
для отклонения гипотезы .
К наиболее
используемым критериям согласия относятся непараметрические критерии типа
Колмогорова, типа 
и 
Мизеса.
В критерии Колмогорова в качестве расстояния между эмпирическим и
теоретическим законом используется величина
,
где
– эмпирическая функция распределения, – теоретическая функция распределения, 
– объём выборки. При проверке гипотез обычно используется
статистика вида [1]
,
где
, 
,
,
-
объем выборки, 
-
упорядоченные по возрастанию выборочные значения, 
- функция закона распределения, согласие с которым
проверяется. Распределение величины 
при
простой гипотезе в пределе подчиняется закону Колмогорова 
[1].
В критериях типа расстояние
между гипотетическим и истинным распределениями рассматривается в
квадратичной метрике
,
где
- оператор математического ожидания.
При выборе 
в
критериях типа Мизеса пользуются статистикой (статистика Крамера-Мизеса-Смирнова) вида
,
которая
при простой гипотезе подчиняется распределению 
[1].
При выборе 
в
критериях типа Мизеса статистика (статистика Андерсона-Дарлинга)
имеет вид
.
В
пределе эта статистика подчиняется распределению 
[1].
В случае простых гипотез предельные распределения
статистик непараметрических критериев типа Колмогорова, и Мизеса известны давно и не зависят от вида наблюдаемого
закона распределения и значений его параметров. Говорят, что эти критерии
являются “свободными от распределения”. Это достоинство предопределяет
широкое использование данных критериев в приложениях.
При проверке
сложных гипотез, когда по той же самой выборке оцениваются параметры
наблюдаемого закона , непараметрические критерии согласия
теряют свойство “свободы от распределения”. Однако, мощность непараметрических
критериев при проверке сложных гипотез при тех же объемах выборок 
всегда существенно выше, чем при
проверке простых. И если при проверке простых гипотез непараметрические
критерии типа Колмогорова, и Мизеса
уступают по мощности критериям типа 
, при
условии, что в последних используется асимптотически оптимальное группирование
[2-5], то при проверке сложных гипотез непараметрические критерии оказываются
более мощными. Для того чтобы воспользоваться их преимуществами, надо только
знать распределение для проверяемой сложной гипотезы.
Различия в
предельных распределениях тех же самых статистик при проверке простых и
сложных гипотез очень существенны. Поэтому предостережения против неаккуратного
применения критериев согласия при проверке сложных гипотез неоднократно
поднимались на страницах печати [6-8]. При проверке сложных гипотез на условный
закон распределения статистики влияет
целый ряд факторов, определяющих “сложность” гипотезы: вид наблюдаемого закона
, соответствующего истинной гипотезе
; тип оцениваемого параметра и количество
оцениваемых параметров; в некоторых ситуациях конкретное значение параметра
(например, в случае гамма-распределения);
используемый метод оценивания параметров и точность вычисления оценок.
Исходной точкой
для исследований предельных распределений статистик непараметрических
критериев согласия при сложных гипотезах послужила работа [9]. В литературных
источниках изложен ряд подходов к использованию непараметрических критериев
согласия в случае проверки сложных гипотез. При достаточно большом объеме
выборки ее можно разбить на две части и по одной из них оценивать параметры, а
по другой проверять согласие [10]. В некоторых частных случаях предельные
распределения статистик исследовались аналитическими методами [11],
процентные точки распределений строились методами статистического моделирования
[12-15]. Для приближенного вычисления вероятностей “согласия” вида 
(достигаемого уровня значимости)
строились формулы, дающие достаточно хорошие приближения при малых значениях
соответствующих вероятностей [16-20]. В наших работах [21-24] исследование
распределений статистик непараметрических критериев согласия и построение
моделей этих распределений осуществлялось с использованием методики
компьютерного анализа статистических закономерностей.
Наши
исследования показали, что распределения статистик критериев согласия
существенно зависят от метода оценивания параметров. Вообще говоря, каждому
типу оценок при конкретной сложной проверяемой гипотезе соответствует своё
предельное распределение статистики.
В случае метода максимального правдоподобия распределения статистик очень сильно зависят от закона,
соответствующего гипотезе . В то же время,
разброс распределений при
использовании MD-оценок, минимизирующих статистику
критерия, в существенно меньшей степени зависит от вида закона , соответствующего гипотезе . Это позволяет говорить об определенной
“свободе от распределения” для рассматриваемых критериев. Если опираться только
на этот факт, то, казалось бы, что только такие методы оценивания и следует
применять при проверке сложных гипотез. Однако исследование мощности рассматриваемых
критериев при различных методах оценивания показало, что наибольшую мощность
данные критерии при близких альтернативах имеют в случае использования оценок
максимального правдоподобия (ОМП).
При малых
объемах выборки 
распределения 
зависят от . Однако, существенная зависимость
распределения статистик от наблюдается
только при небольших объемах выборки. Как показали наши исследования, при 
распределения 
достаточно близки к предельным и зависимостью от можно пренебречь.
Построенные на настоящий момент таблицы процентных точек и предельные распределения статистик непараметрических критериев ограничены относительно узким кругом сложных гипотез. Это объясняется тем, что построение предельного распределения аналитическими методами выливается в чрезвычайно непростую задачу. В то же время методика компьютерного анализа статистических закономерностей, хорошо зарекомендовавшая себя при моделировании распределений статистик критериев [21-24], позволяет при необходимости без существенных трудностей расширить этот круг.
Согласно этой методике следует в соответствии с
законом 
смоделировать
выборок того же объема , что и выборка, для которой необходимо проверить
гипотезу :
. Далее для каждой из выборок вычислить оценки тех же параметров
закона, а затем значение статистики соответствующего
критерия согласия. В результате будет получена выборка значений статистики
с законом распределения для проверяемой гипотезы . По этой выборке при значительных можно построить достаточно гладкую
эмпирическую функцию распределения 
,
которой можно непосредственно воспользоваться для вывода о том, следует ли
принимать гипотезу .
При необходимости можно по 
построить
приближенную аналитическую модель, аппроксимирующую , и тогда уже, опираясь на эту модель, принимать
решение относительно проверяемой гипотезы.
Как показали наши исследования, хорошей аналитической
моделью для часто
оказывается один из следующих четырех законов: логарифмически нормальный, гамма-распредление, распределение Su-Джонсона или
распределение Sl-Джонсона [23-24]. В крайнем случае, всегда можно,
опираясь на ограниченное множество законов распределения, построить модель в
виде смеси этих законов.
В работах [23-24] нами были построены модели предельных распределений статистик рассматриваемых критериев при проверке сложных гипотез относительно 13 различных законов наблюдаемых случайных величин при использовании ОМП и MD-оценок. В данной работе нами получены модели предельных распределений статистик при проверке различных сложных гипотез о согласии с распределениями Sb-, Sl- и Su-Джонсона и использовании ОМП. Модели распределений статистик, построенные в результате применения методики, представлены в таблицах 1-3.
Таблица 1.
|
Модели предельных распределений статистик непараметрических критериев при проверке гипотез о согласии с распределением Sb-Джонсона |
|||
|
Оцениваемые параметры |
Для статистики Колмогорова |
Для статистики
|
Для статистики
|
|
|
lnN(-0,4138; 0,2289) |
lnN(-2,7500; 0,5649) |
Su(-2,7925, 1,5513, 0,1138, 0,1165) |
|
|
lnN(-0,2220; 0,3031) |
Sl (0,9845; 1,1812; 0,2354; 0,0053) |
Su(-3,2608, 1,2469, 0,0836, 0,0883) |
|
|
g(5,2261; 0,0663; 0,2886) |
Su(-2,5137; 1,5524; 0,0159; 0,0118) |
Su(-2,1210; 1,5490; 0,1113; 0,1325) |
В таблицах 1-3, содержащих рекомендуемые для использования
при проверке сложных гипотез распределения через
обозначено логарифмически нормальное распределение
с функцией плотности
,
через
- гамма-распределение с функцией плотности
,
через
- распределение Sl-Джонсона с плотностью
,
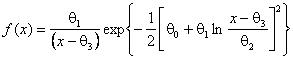через 
- распределение Su-Джонсона с плотностью
.
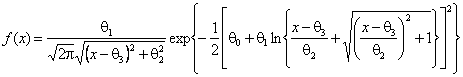Распределение Sb-Джонсона имеет плотность вида
.
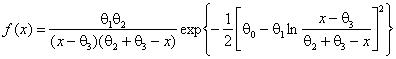Таблица 2.
|
Модели предельных распределений статистик непараметрических критериев при проверке гипотез о согласии с распределением Sl-Джонсона |
|||
|
Оцениваемые параметры |
Для статистики Колмогорова |
Для статистики
|
Для статистики
|
|
|
lnN(-0,4138; 0,2289) |
lnN(-2,7500; 0,5649) |
Su(-2,7925, 1,5513, 0,1138, 0,1165) |
|
|
lnN(-0,2220; 0,3031) |
Sl (0,9845; 1,1812; 0,2354; 0,0053) |
Su(-3,2608, 1,2469, 0,0836, 0,0883) |
|
|
lnN(-0,4138; 0,2289) |
lnN(-2,7500; 0,5649) |
Su(-2,7925, 1,5513, 0,1138, 0,1165) |
|
|
g(5,1416; 0,0672; 0,2886) |
Su(-1,8744; 1,2526; 0,0142; 0,0198) |
Su(-2,3550; 1,5797; 0,1050; 0,1179) |
|
|
lnN(-0,4226; 0,2266) |
lnN(-2,7644; 0,5569) |
Su(-3,0997; 1,5568; 0,0937; 0,1023) |
|
|
g(5,1416; 0,0672; 0,2886) |
Su(-1,8744; 1,2526; 0,0142; 0,0198) |
Su(-2,3550; 1,5797; 0,1050; 0,1179) |
|
|
lnN(-0,4733; 0,2271) |
lnN(-2,9537; 0,5251) |
Su(-1,9900; 1,5211; 0,1145; 0,1445) |
Таблица 3.
|
Модели предельных распределений статистик непараметрических критериев при проверке гипотез о согласии с распределением Su-Джонсона |
|||
|
Оцениваемый параметр |
Распределения статистики Колмогорова |
Распределения статистики
|
Распределения статистики
|
|
|
lnN(-0,4138; 0,2289) |
lnN(-2,7500; 0,5649) |
Su(-2,7925, 1,5513, 0,1138, 0,1165) |
|
|
lnN(-0,2220; 0,3031) |
Sl (0,9845; 1,1812; 0,2354; 0,0053) |
Su(-3,2608, 1,2469, 0,0836, 0,0883) |
|
|
lnN(-0,2594; 0,2990) |
Sl (1,0352; 1,1218; 0,2284; 0,0070) |
Su(-3,0091; 1,1753; 0,0787; 0,1050) |
|
|
lnN(-0,4316; 0,2341) |
Su(-1,7738; 1,2418; 0,0173; 0,0232) |
Su(-2,7823; 1,5327; 0,1140; 0,1125) |
|
|
g(5,2263; 0,0658; 0,2886) |
Su(-1,7649; 1,2854; 0,0151; 0,0208) |
Su(-2,3262; 1,5422; 0,0964; 0,1235) |
|
|
Su(-2,5586; 2,4112; 0,1908; 0,3411) |
lnN(-3,1024; 0,5069) |
Su(-2,1247; 1,4688; 0,0863; 0,1339) |
|
|
Su(-2,3187; 2,2729; 0,1888; 0,3607) |
Su(-1,4187; 1,0120; 0,0117; 0,0232) |
Su(-2,2356; 1,2901; 0,0799; 0,1327) |
|
|
lnN(-0,2836; 0,3039) |
Sl(1,0334; 1,1037; 0,2220; 0,0060) |
Su (-3,1039; 1,1372; 0,062; 0,0950) |
|
|
lnN(-0,5199; 0,2184) |
lnN(-3,0545; 0,5152) |
Sl(0,6951; 1,4454; 0,4295; 0,0818) |
|
|
Su(-2,5904; 2,5548; 0,1859; 0,3300) |
Su(-1,6883; 1,2861; 0,0121; 0,0187) |
Su(-2,1944; 1,3600; 0,0804; 0,1262) |
|
|
Su(-2,1848; 2,1100; 0,1651; 0,3611) |
Su(-1,2247; 1,0971; 0,0120; 0,0228) |
Su(-2,2549; 1,4569; 0,0715; 0,1163) |
|
|
g(4,8573; 0,0568; 0,2890) |
lnN(-3,2677; 0,4767) |
lnN(-1,3166; 0,4065) |
|
|
lnN(-0,6615; 0,1929) |
g(2,6159; 0,0097; 0,0098) |
lnN(-1,4121; 0,3753) |
|
|
lnN(-0,6101; 0,2020) |
Su(-1,5455; 1,2383; 0,0108; 0,0186) |
Su(-2,2203; 1,3198; 0,0646; 0,1203) |
|
|
lnN(-0,7128; 0,1923) |
lnN(-3,5836; 0,4154) |
g(3,6074; 0,0429; 0,0629) |
Рис.
1 иллюстрирует изменение распределений 
статистики
типа Мизеса 
в зависимости от оцениваемого параметра закона
распределения Su-Джонсона.
На рисунке “1” обозначена функция распределения , которому подчиняется статистика при проверке простой
гипотезы, “2” – распределение статистики при проверке сложной гипотезы и
оценивании по данной выборке методом максимального правдоподобия только
параметра 
,
“3” – при оценивании только параметра 
,
“4” – при оценивании только параметра 
,
“5” – при оценивании только параметра 
.
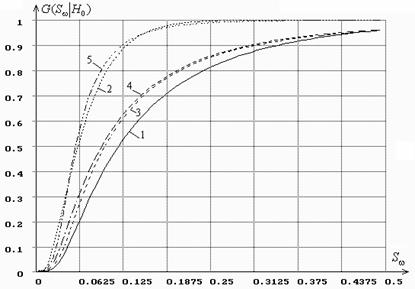
Рис. 1.
На
рис. 2 демонстрируется изменение распределений 
статистики типа Колмогорова 
в зависимости от числа оцениваемых параметров
закона распределения Su-Джонсона.
На данном рисунке “1” отмечена функция распределения Колмогорова, которому
подчиняется статистика при проверке простой гипотезы, “2” – распределение
статистики при проверке сложной гипотезы и оценивании по данной выборке методом
максимального правдоподобия только параметра , “3” – при оценивании только параметров и ,
“4” – при оценивании параметров , и ,
“5” – при оценивании всех четырех параметров ,,,.
Как
можно убедиться на основании построенных закономерностей, распределения
статистик непараметрических критериев согласия существенно зависят от вида и
числа оцениваемых параметров. И даже при оценивании единственного параметра
предельное распределение статистики резко отличается от предельного распределения
той же самой статистики в случае проверки простой гипотезы. Различие возрастает
с увеличением числа оцениваемых параметров. Пренебрежение этим фактом в
практике применения критериев согласия приводит к большим ошибкам в вычислении
вероятности вида и
неоправданному принятию проверяемой гипотезы.
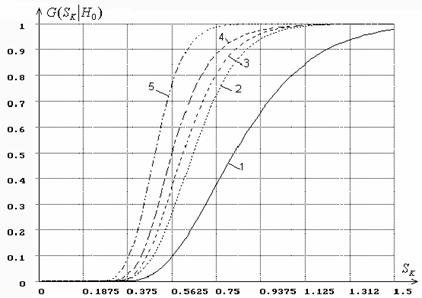
Рис. 2.
Заключение
Построенные аппроксимации предельных распределений статистик непараметрических критериев согласия дополняют результаты, представленные в рекомендациях [24], расширяют область корректного применения этих критериев и могут быть рекомендованы широкому кругу исследователей. Апробированная методика моделирования распределений статистик может быть рекомендована для построения статистических закономерностей в ситуации, когда аналитическими методами не удается решить задачу.
ЛИТЕРАТУРА
[1] Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
[2] Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун–т. – Новосибирск, 1993. – 346 с.
[3] Лемешко Б.Ю. // Надежность и контроль качества. – 1997. – № 8. – С. 3–14.
[4] Лемешко Б.Ю. // Заводская лаборатория. – 1998. – Т. 64. – №1. – С. 56-64.
[5] Денисов
В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки
согласия опытного распределения с теоретическим: Методические рекомендации.
Часть I. Критерии типа 
. – Новосибирск:
Изд–во НГТУ, 1998. – С. 126.
[6] Орлов А.И. // Заводская лаборатория. – 1985. – Т. 51. – №1. – С. 60-62.
[7] Бондарев Б.В. // Заводская лаборатория. – 1986. – Т. 52. – № 10. – С. 62-63.
[8] Кулинская Е.В., Саввушкина Н.Е. // Заводская лаборатория. – 1990. – Т. 56. – № 5. – С. 96-99.
[9] Kac M., Kiefer J., Wolfowitz J. // Ann. Math. Stat. – 1955. – V.26. –
P.189-211.
[10] Durbin J. // Lect. Notes Math. – 1976. – V. 566. – P. 33–44.
[11] Мартынов Г.В. Критерии омега–квадрат. – М.: Наука, 1978. – 80 с.
[12] Pearson E.S., Hartley H.O. Biometrica
tables for Statistics. V.2. –
[13] Stephens M.A. // J. R. Stat. Soc. – 1970. – B.
32. – P. 115-122.
[14] Stephens M.A. // J. Am. Statist. Assoc. – 1974. –
V.69. – P. 730-737.
[15] Chandra M.,
[16] Тюрин Ю.Н. // Изв. АН СССР. Сер. Матем. – 1984. – Т. 48. – № 6. – C. 1314-1343.
[17] Тюрин Ю.Н., Саввушкина Н.Е. // Изв. АН СССР. Сер. Техн. Кибернетика. – 1984. – № 3. – C. 109-112.
[18] Тюрин Ю.Н. Исследования по непараметрической статистике (непараметрические методы и линейная модель): Автореф. дисс. … д–ра физ.–мат. наук. – М., 1985. – 33 с. – (МГУ).
[19] Саввушкина Н.Е. Критерий Колмогорова–Смирнова для логистического и гамма–распределения // Сб. тр. ВНИИ систем. исслед. – 1990, № 8.
[20] Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. // М.: ИНФРА–М, Финансы и статистика, 1995. – 384 с.
[21] Лемешко Б.Ю., Постовалов С.Н. // Надежность и контроль качества. – 1997. – № 11. – С. 3-17.
[22] Лемешко Б.Ю., Постовалов С.Н. Исследование допредельных распределений статистик критериев согласия при проверке сложных гипотез // Тр. IV международной конференции “Актуальные проблемы электронного приборостроения”. – Новосибирск. – 1998. – Т. 3. – С. 12-16.
[23] Лемешко Б.Ю., Постовалов С.Н. // Заводская лаборатория. – 1998. – Т. 64. – № 3. – С. 61-72.
[24] Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ. – 1999. – 86 с.
[1] Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 00-01-00913)