См. также: Прикладная математическая статистика (материалы
к семинарам)
Измерительная техника. 2002. - № 6. - С.
5-11.
УДК
519.2
ОБ ОШИБКАХ И НЕВЕРНЫХ ДЕЙСТВИЯХ, СОВЕРШАЕМЫХ ПРИ
ИСПОЛЬЗОВАНИИ КРИТЕРИЕВ СОГЛАСИЯ ТИПА ![]() [1]
[1]
Лемешко Б.Ю., Чимитова
Е.В.
Проверка статистических гипотез о согласии
эмпирических данных с теоретическим законом распределения с применением
критериев согласия типа ![]() обусловлена
рядом условий, которые обеспечивают корректное решение задачи. К сожалению,
не в каждом источнике, который используется в качестве руководства
исследователем, находят отражение эти условия. Вследствие этого, не смотря на
кажущуюся простоту, практика использования критериев согласия типа
обусловлена
рядом условий, которые обеспечивают корректное решение задачи. К сожалению,
не в каждом источнике, который используется в качестве руководства
исследователем, находят отражение эти условия. Вследствие этого, не смотря на
кажущуюся простоту, практика использования критериев согласия типа ![]() изобилует примерами его некорректного или
неэффективного применения, особенно при проверке сложных гипотез.
изобилует примерами его некорректного или
неэффективного применения, особенно при проверке сложных гипотез.
Анализ примеров “неудачного” применения критериев типа
![]() позволяет выделить две группы причин, которые
могут приводить к неверным статистическим выводам. Во-первых, это часто
совершаемые принципиальные ошибки, при которых использование в качестве
предельного
позволяет выделить две группы причин, которые
могут приводить к неверным статистическим выводам. Во-первых, это часто
совершаемые принципиальные ошибки, при которых использование в качестве
предельного ![]() -распределения оказывается неправомерным. Во-вторых,
действия, использующие возможности критерия не наилучшим образом. В первом
случае возрастает вероятность ошибки первого рода
-распределения оказывается неправомерным. Во-вторых,
действия, использующие возможности критерия не наилучшим образом. В первом
случае возрастает вероятность ошибки первого рода ![]() (отклонить верную проверяемую гипотезу), во
втором – вероятность ошибки второго рода
(отклонить верную проверяемую гипотезу), во
втором – вероятность ошибки второго рода ![]() (принять
проверяемую гипотезу при справедливости альтернативы).
(принять
проверяемую гипотезу при справедливости альтернативы).
При использовании критериев согласия возможна проверка простых гипотез вида ![]() :
: ![]() ,
где
,
где ![]() – функция распределения вероятностей, с
которой проверяется согласие наблюдаемой выборки независимых одинаково
распределенных величин
– функция распределения вероятностей, с
которой проверяется согласие наблюдаемой выборки независимых одинаково
распределенных величин ![]() ,
а
,
а ![]() – известное значение параметра (скалярного или
векторного), и сложных гипотез
– известное значение параметра (скалярного или
векторного), и сложных гипотез ![]() :
: ![]() , где
, где ![]() –
пространство параметров. В процессе проверки сложной гипотезы оценка
параметра
–
пространство параметров. В процессе проверки сложной гипотезы оценка
параметра ![]() вычисляется по этой же самой выборке.
вычисляется по этой же самой выборке.
Процедура проверки гипотез с помощью критериев типа ![]() предусматривает разбиение области определения
случайной величины на
предусматривает разбиение области определения
случайной величины на ![]() интервалов граничными точками
интервалов граничными точками
![]() .
.
Статистика ![]() Пирсона вычисляется в соответствии с соотношением
Пирсона вычисляется в соответствии с соотношением
![]() ,
(1)
,
(1)
где
![]() – количество наблюдений, попавших в
– количество наблюдений, попавших в ![]() -й
интервал,
-й
интервал, 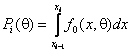 – вероятность попадания наблюдения в
– вероятность попадания наблюдения в ![]() -й интервал,
-й интервал, ![]() ,
, ![]() .
При справедливой простой гипотезе
.
При справедливой простой гипотезе ![]() предельное
распределение статистики
предельное
распределение статистики ![]() есть
есть
![]() -распределение с числом степеней свободы
-распределение с числом степеней свободы ![]() . Если по выборке оценивалось
. Если по выборке оценивалось ![]() параметров закона в результате минимизации
статистики
параметров закона в результате минимизации
статистики ![]() , статистика подчиняется
, статистика подчиняется ![]() -распределению с
-распределению с ![]() степенями
свободы. При справедливости некоторой альтернативной гипотезы
степенями
свободы. При справедливости некоторой альтернативной гипотезы ![]() предельное распределение статистики
предельное распределение статистики ![]() представляет собой нецентральное
представляет собой нецентральное ![]() -распределение с тем же числом степеней свободы и
параметром нецентральности
-распределение с тем же числом степеней свободы и
параметром нецентральности
![]() ,
(2)
,
(2)
где
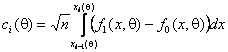 и
и ![]() соответствует
альтернативе.
соответствует
альтернативе.
Первоначально предполагалось, что в случае проверки сложных гипотез и
оценивании по выборке параметров наблюдаемого закона использование в
качестве предельных ![]() -распределений справедливо лишь при определении оценок
минимизацией статистики
-распределений справедливо лишь при определении оценок
минимизацией статистики ![]() .
Позднее было доказано, что статистика
.
Позднее было доказано, что статистика ![]() подчиняется
подчиняется
![]() -распределению
и в том случае, если используются оценки максимального правдоподобия (ОМП) по
группированным наблюдениям [1-3].
-распределению
и в том случае, если используются оценки максимального правдоподобия (ОМП) по
группированным наблюдениям [1-3].
Наши исследования методами статистического моделирования распределений
данной статистики при проверке сложных гипотез и использовании ОМП по
группированным наблюдениям (при конечных объемах выборок) также подтвердили
хорошее согласие получаемых эмпирических распределений статистики с ![]() -распределениями.
Кроме того, наши исследования показали, что есть все основания использовать
-распределениями.
Кроме того, наши исследования показали, что есть все основания использовать ![]() -распределения
в качестве предельных распределений статистики
-распределения
в качестве предельных распределений статистики ![]() и в том случае, если
параметры сдвига и масштаба наблюдаемых законов случайных величин будут
находиться в виде линейных комбинаций выборочных квантилей (L-оценок
[4] и оптимальных L-оценок [5]).
и в том случае, если
параметры сдвига и масштаба наблюдаемых законов случайных величин будут
находиться в виде линейных комбинаций выборочных квантилей (L-оценок
[4] и оптимальных L-оценок [5]).
При проведении данных исследований использовались программная система
[6] и ее дальнейшие версии [7] и [8], в которых реализован ряд критериев
проверки согласия эмпирического распределения с теоретической моделью: ![]() Пирсона, отношения
правдоподобия, Колмогорова, Смирнова,
Пирсона, отношения
правдоподобия, Колмогорова, Смирнова, ![]() и
и
![]() Мизеса, Никулина. Здесь и ниже, когда мы употребляем
словосочетание “хорошее согласие”, то подразумеваем, что по всем критериям
достигнутый уровень значимости, определяемый соотношением
Мизеса, Никулина. Здесь и ниже, когда мы употребляем
словосочетание “хорошее согласие”, то подразумеваем, что по всем критериям
достигнутый уровень значимости, определяемый соотношением
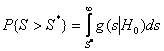 ,
,
где ![]() - значение статистики
критерия, вычисленное по наблюдаемой выборке,
- значение статистики
критерия, вычисленное по наблюдаемой выборке, ![]() - плотность предельного
распределения статистики соответствующего критерия при справедливости гипотезы
- плотность предельного
распределения статистики соответствующего критерия при справедливости гипотезы ![]() , был очень высок:
, был очень высок: ![]() ³0,6-0,9.
³0,6-0,9.
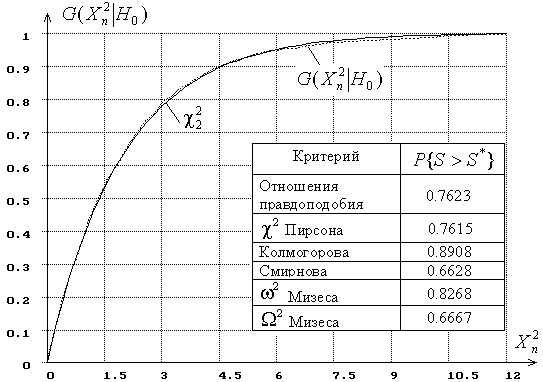
Рис. 1
Например, на рис. 1 представлены результаты моделирования распределения
статистики ![]() при
вычислении оптимальных L-оценок [5] двух параметров нормального
распределения при числе интервалов
при
вычислении оптимальных L-оценок [5] двух параметров нормального
распределения при числе интервалов ![]() .
На рисунке приведены построенная в результате моделирования эмпирическая
функция распределения статистики
.
На рисунке приведены построенная в результате моделирования эмпирическая
функция распределения статистики ![]() ,
функция теоретического
,
функция теоретического ![]() -распределения и значения достигнутого уровня значимости
-распределения и значения достигнутого уровня значимости ![]() при проверке согласия по
каждому из используемых критериев.
при проверке согласия по
каждому из используемых критериев.
Следует полагать, что применение ![]() -распределений в качестве предельных распределений
оказывается оправданным и при использовании ряда других оценок,
предусматривающих группирование наблюдений, в частности, при нахождении
оценок в результате минимизации модифицированной статистики
-распределений в качестве предельных распределений
оказывается оправданным и при использовании ряда других оценок,
предусматривающих группирование наблюдений, в частности, при нахождении
оценок в результате минимизации модифицированной статистики ![]() [9]
[9]
![]() ,
,
где
![]() заменяется на 1, если
заменяется на 1, если ![]() , в результате минимизации расстояния Хеллингера [9]
, в результате минимизации расстояния Хеллингера [9]
![]() ,
,
в результате минимизации дивергенции Кульбака-Лейблера (информации Кульбака-Лейблера) [9]
![]() .
.
Асимптотические
свойства этих оценок эквивалентны свойствам ОМП по группированным наблюдениям и
оценкам, минимизирующим статистику ![]() . Результаты статистического моделирования
подтвердили, что и при использовании данных оценок статистика
. Результаты статистического моделирования
подтвердили, что и при использовании данных оценок статистика ![]() подчиняется
подчиняется ![]() -распределениям.
-распределениям.
Если же оценки параметров искать по точечным выборкам
(по исходным негруппированным наблюдениям), то предельные
распределения статистики ![]() не являются
не являются ![]() -распределениями.
Более того, распределения статистики
-распределениями.
Более того, распределения статистики ![]() становятся
зависящими от того, как разбивается область определения случайной величины на
интервалы [10]. Как выглядят распределения статистики
становятся
зависящими от того, как разбивается область определения случайной величины на
интервалы [10]. Как выглядят распределения статистики ![]() при использовании ОМП по точечным выборкам по
сравнению с
при использовании ОМП по точечным выборкам по
сравнению с ![]() -распределениями иллюстрирует рис. 2, на котором
приведены распределения
-распределениями иллюстрирует рис. 2, на котором
приведены распределения ![]() при
асимптотически оптимальном группировании (АОГ) [11-13] и при разбиении на
интервалы равной вероятности (РВГ) в случае проверки согласия с нормальным
распределением с оцениванием двух его параметров и числе интервалов
при
асимптотически оптимальном группировании (АОГ) [11-13] и при разбиении на
интервалы равной вероятности (РВГ) в случае проверки согласия с нормальным
распределением с оцениванием двух его параметров и числе интервалов ![]() . При оценивании параметров нормального закона по
группированной выборке статистика
. При оценивании параметров нормального закона по
группированной выборке статистика ![]() подчинялась
бы в данном случае
подчинялась
бы в данном случае ![]() -распределению.
Как подчеркивает рис. 2, распределения статистики
-распределению.
Как подчеркивает рис. 2, распределения статистики ![]() и
и ![]() очень
существенно отличаются от
очень
существенно отличаются от ![]() -распределения.
Игнорирование этого факта на практике часто приводит к неоправданному
отклонению проверяемой гипотезы, к увеличению вероятности ошибок первого
рода.
-распределения.
Игнорирование этого факта на практике часто приводит к неоправданному
отклонению проверяемой гипотезы, к увеличению вероятности ошибок первого
рода.
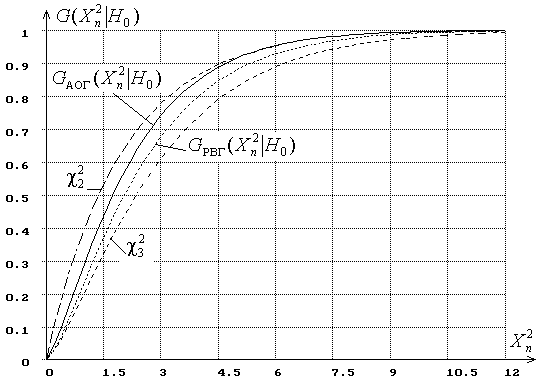
Рис. 2
К сожалению, примеров, содержащих принципиальные
ошибки применения критериев типа ![]() с
использованием ОМП по точечным выборкам или оценок по методу моментов можно
привести очень много. Не в последнюю очередь, это объясняется и тем, что такие
ошибки часто содержатся в литературе учебного характера, рассчитанной на
широкий круг читателей [14-15], тиражируются в учебных пособиях и курсах лекций.
Не всегда уделяется этому внимание при обработке измерительной информации и
исследовании законов распределения ошибок измерений [16].
с
использованием ОМП по точечным выборкам или оценок по методу моментов можно
привести очень много. Не в последнюю очередь, это объясняется и тем, что такие
ошибки часто содержатся в литературе учебного характера, рассчитанной на
широкий круг читателей [14-15], тиражируются в учебных пособиях и курсах лекций.
Не всегда уделяется этому внимание при обработке измерительной информации и
исследовании законов распределения ошибок измерений [16].
Среди критериев типа ![]() существует
критерий, который предусматривает вычисление ОМП по точечным выборкам. В своем
роде это уникальный критерий, так как является единственным из всех известных,
обладающим свойством “свободы от распределения” при проверке сложных гипотез.
Это критерий, предложенный С.М. Никулиным. Статистика типа
существует
критерий, который предусматривает вычисление ОМП по точечным выборкам. В своем
роде это уникальный критерий, так как является единственным из всех известных,
обладающим свойством “свободы от распределения” при проверке сложных гипотез.
Это критерий, предложенный С.М. Никулиным. Статистика типа ![]() Никулина [17-20] отличается от
Никулина [17-20] отличается от
![]() при сложных гипотезах. Предельное распределение
этой статистики – обычное распределение
при сложных гипотезах. Предельное распределение
этой статистики – обычное распределение ![]() (количество
степеней свободы не зависит от числа оцениваемых параметров!). Неизвестные
параметры распределения
(количество
степеней свободы не зависит от числа оцениваемых параметров!). Неизвестные
параметры распределения ![]() в
этом случае должны оцениваться по исходной точечной выборке методом
максимального правдоподобия. Вектор вероятностей попадания в интервалы
в
этом случае должны оцениваться по исходной точечной выборке методом
максимального правдоподобия. Вектор вероятностей попадания в интервалы ![]() предполагается заданным, и границы интервалов
определяются выражениями
предполагается заданным, и границы интервалов
определяются выражениями ![]() ,
, ![]() .
.
Данная статистика имеет вид [17]
![]() ,
(3)
,
(3)
где
![]() вычисляется в соответствии с (1). Элементы и
размерность матрицы
вычисляется в соответствии с (1). Элементы и
размерность матрицы
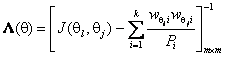
определяются
оцениваемыми компонентами вектора параметров ![]() ,
, ![]() -
элементы информационной матрицы
-
элементы информационной матрицы
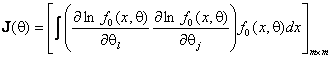 ,
,
![]() -
элементы вектора
-
элементы вектора ![]() , величины
, величины ![]() определяются
соотношением
определяются
соотношением
![]() .
.
При справедливости конкурирующей гипотезы статистика ![]() подчиняется в качестве предельного
подчиняется в качестве предельного ![]() нецентральному
нецентральному ![]() -распределению с параметром нецентральности
-распределению с параметром нецентральности
![]() ,
(4)
,
(4)
где
вектор ![]() с элементами
с элементами ![]() .
.
Распределения статистики Никулина ![]() и
и ![]() практически не зависят от
способа разбиения области определения случайной величины на интервалы [21]. Мощность критерия Никулина при
близких альтернативах выше мощности критерия Пирсона. Это значит, что с его
помощью лучше различаются близкие гипотезы.
практически не зависят от
способа разбиения области определения случайной величины на интервалы [21]. Мощность критерия Никулина при
близких альтернативах выше мощности критерия Пирсона. Это значит, что с его
помощью лучше различаются близкие гипотезы.
Практическое применение критерия Никулина связано с
несколько большими вычислительными затратами по сравнению с критерием ![]() Пирсона. Кроме того, вычисление статистики (3)
при проверке конкретной гипотезы требует от пользователя проведения
определенных математических выкладок, что может оказаться несколько
затруднительным. Рекомендуемый выход видится в создании соответствующего
программного обеспечения, включении его в программные системы задач статистического
анализа, как это сделано в [7,8]. В конечном счете, это оказывается оправданным
замечательными свойствами критерия.
Пирсона. Кроме того, вычисление статистики (3)
при проверке конкретной гипотезы требует от пользователя проведения
определенных математических выкладок, что может оказаться несколько
затруднительным. Рекомендуемый выход видится в создании соответствующего
программного обеспечения, включении его в программные системы задач статистического
анализа, как это сделано в [7,8]. В конечном счете, это оказывается оправданным
замечательными свойствами критерия.
Все вышесказанное о предотвращении принципиальных ошибок направлено на
уменьшение вероятности ошибок первого рода. Но можно говорить и о снижении
вероятности ошибок второго рода, о повышении мощности критериев типа ![]() .
.
При использовании критериев согласия типа ![]() неоднозначность в построении и вычислении
статистик связана с выбором числа интервалов и с тем, каким образом область
определения случайной величины разбивается на интервалы (с выбором граничных
точек интервалов). Такой произвол отражается на статистических свойствах
применяемых критериев согласия и, в частности, на мощности критериев, на их
способности различать близкие конкурирующие гипотез. Очевидно, что выбор
числа интервалов и способа разбиения на интервалы следует осуществлять с
позиций обеспечения максимальной мощности применяемого критерия. Однако
этому не уделяется внимания ни в регламентирующих документах, ни в
литературных источниках.
неоднозначность в построении и вычислении
статистик связана с выбором числа интервалов и с тем, каким образом область
определения случайной величины разбивается на интервалы (с выбором граничных
точек интервалов). Такой произвол отражается на статистических свойствах
применяемых критериев согласия и, в частности, на мощности критериев, на их
способности различать близкие конкурирующие гипотез. Очевидно, что выбор
числа интервалов и способа разбиения на интервалы следует осуществлять с
позиций обеспечения максимальной мощности применяемого критерия. Однако
этому не уделяется внимания ни в регламентирующих документах, ни в
литературных источниках.
Способ группирования оказывает особенно сильное
влияние на предельное распределение ![]() . В работах [11-13, 22-23] показано, что критерии согласия
. В работах [11-13, 22-23] показано, что критерии согласия ![]() Пирсона и
отношения правдоподобия [24] при проверке как простых, так и сложных гипотез имеют
максимальную мощность против близких альтернатив, если использовать такое
разбиение области определения случайной величины на интервалы, при котором
минимальны потери в информации Фишера о параметрах закона, соответствующего
гипотезе
Пирсона и
отношения правдоподобия [24] при проверке как простых, так и сложных гипотез имеют
максимальную мощность против близких альтернатив, если использовать такое
разбиение области определения случайной величины на интервалы, при котором
минимальны потери в информации Фишера о параметрах закона, соответствующего
гипотезе ![]() (асимптотически оптимальное группирование). Чем
меньше потери в информации Фишера, связанные с группированием данных, тем
больше параметр нецентральности, определяемый соотношением
(2). В [11, 23] для конкретных законов распределения представлен достаточно
широкий состав построенных таблиц асимптотически оптимального группирования
(АОГ-группирования), минимизирующего
потери в информации Фишера. Таблицы асимптотически оптимального группирования
(58 таблиц) доступны читателям журнала на WEB-сайте [25]. При построении этих
таблиц максимизировался определитель информационной
матрицы Фишера по группированным наблюдениям, которая определяется
соотношением
(асимптотически оптимальное группирование). Чем
меньше потери в информации Фишера, связанные с группированием данных, тем
больше параметр нецентральности, определяемый соотношением
(2). В [11, 23] для конкретных законов распределения представлен достаточно
широкий состав построенных таблиц асимптотически оптимального группирования
(АОГ-группирования), минимизирующего
потери в информации Фишера. Таблицы асимптотически оптимального группирования
(58 таблиц) доступны читателям журнала на WEB-сайте [25]. При построении этих
таблиц максимизировался определитель информационной
матрицы Фишера по группированным наблюдениям, которая определяется
соотношением
![]() .
.
Использование АОГ-группирования при фиксированном числе интервалов обеспечивает максимальную мощность при близких гипотезах.
Исследование распределений статистики ![]() Никулина, которая
отличается от
Никулина, которая
отличается от ![]() только
при сложных гипотезах, показало, что как
только
при сложных гипотезах, показало, что как ![]() , так и
, так и ![]() несущественно зависят от
способа группирования [21]. Более того, наши исследования показали, что с
позиций наибольшей мощности разбиение на интервалы равной вероятности (РВГ-группирование) оказывается наиболее предпочтительным.
Еще раз подчеркнем, что критерий типа
несущественно зависят от
способа группирования [21]. Более того, наши исследования показали, что с
позиций наибольшей мощности разбиение на интервалы равной вероятности (РВГ-группирование) оказывается наиболее предпочтительным.
Еще раз подчеркнем, что критерий типа ![]() Никулина
мощнее, чем критерии
Никулина
мощнее, чем критерии ![]() Пирсона
и отношения правдоподобия.
Пирсона
и отношения правдоподобия.
Мощность критериев типа ![]() существенно зависит от числа интервалов
существенно зависит от числа интервалов ![]() . Давно известно [26, 27], что, начиная с некоторого
значения, при дальнейшем росте числа интервалов
. Давно известно [26, 27], что, начиная с некоторого
значения, при дальнейшем росте числа интервалов ![]() мощность падает. Вообще говоря, для каждой пары
альтернатив можно подобрать оптимальное значение числа интервалов, которое
зависит от этой пары альтернатив, способа группирования и объема выборки
мощность падает. Вообще говоря, для каждой пары
альтернатив можно подобрать оптимальное значение числа интервалов, которое
зависит от этой пары альтернатив, способа группирования и объема выборки ![]() . Для определения числа интервалов предлагалось
достаточно много эмпирических формул, обширный перечень которых приводится в
[16]. При выводе и построении этих формул опирались на различные требования, но
никогда – на требование максимальной мощности. На основании этих формул
получают различные, возрастающие с ростом объема выборки рекомендуемые числа
интервалов. Причем, далеко не оптимальные, чаще всего
существенно завышенные.
. Для определения числа интервалов предлагалось
достаточно много эмпирических формул, обширный перечень которых приводится в
[16]. При выводе и построении этих формул опирались на различные требования, но
никогда – на требование максимальной мощности. На основании этих формул
получают различные, возрастающие с ростом объема выборки рекомендуемые числа
интервалов. Причем, далеко не оптимальные, чаще всего
существенно завышенные.
Зная предельные распределения ![]() и
и ![]() статистики
статистики
![]() , для любого заданного уровня значимости
, для любого заданного уровня значимости ![]() можно оценить мощность соответствующего
критерия, рассматривая её как функцию от числа интервалов
можно оценить мощность соответствующего
критерия, рассматривая её как функцию от числа интервалов ![]() при заданном объеме выборки
при заданном объеме выборки ![]() . В работе [28] было проведено исследование мощности
критериев Пирсона и Никулина как функции от
. В работе [28] было проведено исследование мощности
критериев Пирсона и Никулина как функции от ![]() и
и ![]() аналитически
и методами статистического моделирования. Причем
результаты аналитических вычислений оказались полностью подтвержденными
оценками мощности, полученными на основании моделирования.
аналитически
и методами статистического моделирования. Причем
результаты аналитических вычислений оказались полностью подтвержденными
оценками мощности, полученными на основании моделирования.
Величина мощности для критериев типа ![]() может
быть вычислена в соответствии с выражением [29]:
может
быть вычислена в соответствии с выражением [29]:
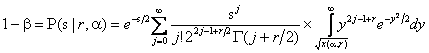 (5)
(5)
где
![]() - параметр нецентральности,
определяемый соотношениями (2) и (4),
- параметр нецентральности,
определяемый соотношениями (2) и (4), ![]() представляет
собой
представляет
собой ![]() -процентную точку
-процентную точку ![]() -распределения
с
-распределения
с ![]() степенями свободы (
степенями свободы (![]() - заданная вероятность ошибки первого рода,
- заданная вероятность ошибки первого рода, ![]() - вероятность ошибки второго рода). Все
приводимые ниже функции мощности строились при уровне значимости
- вероятность ошибки второго рода). Все
приводимые ниже функции мощности строились при уровне значимости ![]() .
.
На рис. 3 в зависимости от числа интервалов ![]() при равновероятном и асимптотически оптимальном
группировании для объема выборок
при равновероятном и асимптотически оптимальном
группировании для объема выборок ![]() , равного
500 и 5000, представлены функции мощности критерия
, равного
500 и 5000, представлены функции мощности критерия ![]() Пирсона при проверке простой гипотезы о согласии
с экспоненциальным законом (
Пирсона при проверке простой гипотезы о согласии
с экспоненциальным законом (![]() :
: ![]() при
при ![]() ; против
; против ![]() :
: ![]() при
при ![]() ).
И в том, и в другом случае с ростом
).
И в том, и в другом случае с ростом ![]() мощность
падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
мощность
падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
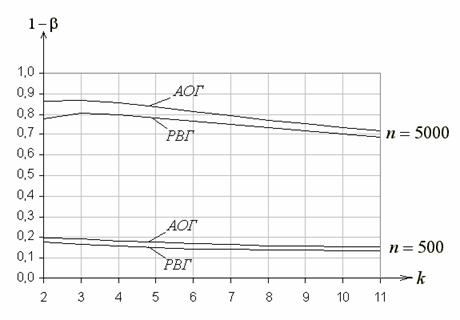
Рис. 3
Аналогично, на рис. 4 приведены функции мощности
критерия ![]() Пирсона как функции числа интервалов
Пирсона как функции числа интервалов ![]() для
для ![]() ,
равного 300 и 2000, при проверке простой гипотезы относительно нормального
закона (
,
равного 300 и 2000, при проверке простой гипотезы относительно нормального
закона (![]() :
: 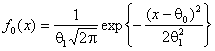 при
при ![]() ,
, ![]() ; против
; против ![]() :
нормальный закон при
:
нормальный закон при ![]() ,
, ![]() ).
).
На рис. 5 приведены функции мощности критерия ![]() Пирсона при проверке сложной гипотезы о согласии
с распределением Вейбулла. Рассматривались гипотеза
Пирсона при проверке сложной гипотезы о согласии
с распределением Вейбулла. Рассматривались гипотеза ![]() :
: 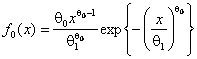 при
при ![]() ,
, ![]() и близкая альтернатива – распределение Накагами
и близкая альтернатива – распределение Накагами ![]() :
: 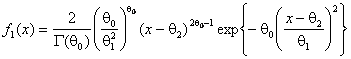 при
при ![]() ,
, ![]() ,
, ![]() .
.
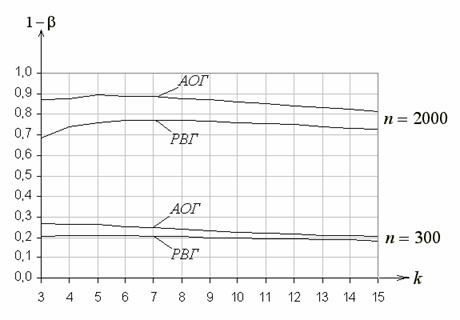
Рис. 4
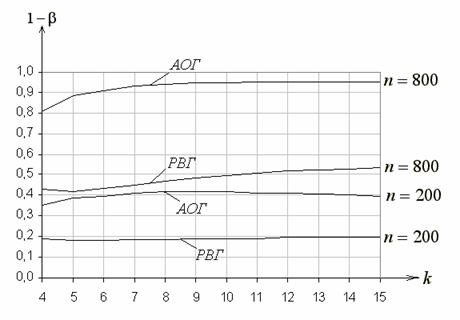
Рис. 5
Рис. 6 иллюстрирует поведение функции мощности
критерия типа ![]() Никулина при использовании равновероятного
группирования и проверке сложной гипотезы о согласии с нормальным законом
Никулина при использовании равновероятного
группирования и проверке сложной гипотезы о согласии с нормальным законом
![]() :
: 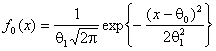 ,
,
когда в качестве альтернативы рассматривается близкий ему логистический закон
![]() :
: 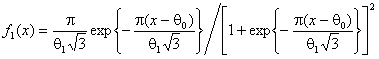
при
значениях параметров ![]() ,
, ![]() .
.
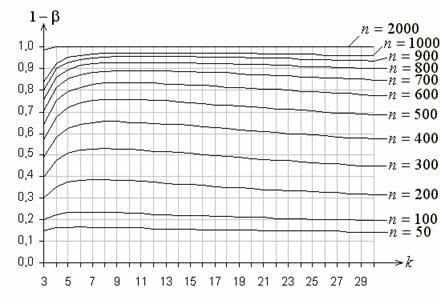
Рис. 6
Еще раз подчеркнем, что результаты статистического моделирования
функций распределения ![]() и
и
![]() для
статистик
для
статистик ![]() рассматриваемых
критериев типа
рассматриваемых
критериев типа ![]() дают
оценки мощности очень близкие к расчетным значениям функции мощности по
соотношению (5).
дают
оценки мощности очень близкие к расчетным значениям функции мощности по
соотношению (5).
Способность любых статистических критериев различать
гипотезы, то есть их мощность, возрастает с ростом объема выборок. При малых ![]() бывает очень трудно, различить пару близких
гипотез, так как очень близкими оказываются распределения
бывает очень трудно, различить пару близких
гипотез, так как очень близкими оказываются распределения ![]() и
и ![]() .
Любой практик может заметить, что при малых
.
Любой практик может заметить, что при малых ![]() с
равным успехом могут быть приняты гипотезы о согласии с целым рядом существенно
отличающихся моделей законов распределений. Поэтому при малых объемах выборок
любой выигрыш в мощности за счет корректного применения критерия особенно ценен.
с
равным успехом могут быть приняты гипотезы о согласии с целым рядом существенно
отличающихся моделей законов распределений. Поэтому при малых объемах выборок
любой выигрыш в мощности за счет корректного применения критерия особенно ценен.
Несколько слов о принятии решения по результатам проверки гипотез. В широко
распространенной практике статистического анализа обычно сравнивают
вычисленное значение статистики ![]() с
критическим
с
критическим ![]() для
данного уровня значимости
для
данного уровня значимости ![]() и
нулевую гипотезу отвергают, если
и
нулевую гипотезу отвергают, если ![]() .
Критическое значение
.
Критическое значение ![]() ,
определяемое из уравнения
,
определяемое из уравнения
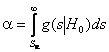 ,
,
обычно берётся из соответствующей статистической таблицы.
Естественно, что больше информации о степени согласия
можно почерпнуть из величины вероятности возможного превышения полученного
значения статистики при истинности нулевой гипотезы: 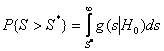 . Иногда эту вероятность называют достигнутым
уровнем значимости. Именно она позволяет судить о том, насколько хорошо выборка
согласуется с теоретическим распределением, так как по существу представляет
собой вероятность истинности нулевой гипотезы. Чем больше величина
. Иногда эту вероятность называют достигнутым
уровнем значимости. Именно она позволяет судить о том, насколько хорошо выборка
согласуется с теоретическим распределением, так как по существу представляет
собой вероятность истинности нулевой гипотезы. Чем больше величина ![]() , тем лучше. Именно она определяет степень нашей
уверенности в том, что предполагаемая модель закона является истинной. Гипотеза
о согласии не должна отвергаться, если
, тем лучше. Именно она определяет степень нашей
уверенности в том, что предполагаемая модель закона является истинной. Гипотеза
о согласии не должна отвергаться, если ![]() .
.
Поэтому мы рекомендуем при проверке любых гипотез
принимать решение на основании найденного значения ![]() , для чего можно или воспользоваться таблицей
соответствующего распределения, или использовать какой-либо статистический
пакет программ.
, для чего можно или воспользоваться таблицей
соответствующего распределения, или использовать какой-либо статистический
пакет программ.
Заключение
Таким образом, если Вы, применяя критерии типа ![]() , стремитесь обеспечить корректность статистических
выводов при обработке измерительной информации, следует обратить внимание на
следующие три момента.
, стремитесь обеспечить корректность статистических
выводов при обработке измерительной информации, следует обратить внимание на
следующие три момента.
Во-первых, на то, по каким данным вычисляются оценки
при проверке сложных гипотез. Предельными ![]() -распределениями
для критериев
-распределениями
для критериев ![]() Пирсона и отношения правдоподобия можно
пользоваться только при оценивании параметров по группированным наблюдениям. Если
Вы в силу понятных причин отдаете предпочтение ОМП по точечным наблюдениям,
целесообразней воспользоваться критерием Никулина. Используя в данной ситуации
критерии
Пирсона и отношения правдоподобия можно
пользоваться только при оценивании параметров по группированным наблюдениям. Если
Вы в силу понятных причин отдаете предпочтение ОМП по точечным наблюдениям,
целесообразней воспользоваться критерием Никулина. Используя в данной ситуации
критерии ![]() Пирсона и отношения правдоподобия, следует
помнить, что величина вероятности
Пирсона и отношения правдоподобия, следует
помнить, что величина вероятности ![]() ,
вычисленная в соответствии с
,
вычисленная в соответствии с ![]() -распределением,
оказывается заниженной по сравнению с истинной.
-распределением,
оказывается заниженной по сравнению с истинной.
Во-вторых, на то, каким образом разбить область
определения случайной величины на интервалы. Использование асимптотически оптимального
группирования максимизирует мощность критериев ![]() Пирсона и отношения правдоподобия по отношению к
близким гипотезам в случае простых и сложных гипотез. Кроме того, применение
таблиц асимптотически оптимального группирования [11, 23, 25], благодаря тому,
что они содержат значения вероятностей попадания в интервал, облегчает и
процесс вычислений. В случае критерия Никулина можно воспользоваться или
асимптотически оптимальным группированием или разбиением на интервалы равных
вероятностей.
Пирсона и отношения правдоподобия по отношению к
близким гипотезам в случае простых и сложных гипотез. Кроме того, применение
таблиц асимптотически оптимального группирования [11, 23, 25], благодаря тому,
что они содержат значения вероятностей попадания в интервал, облегчает и
процесс вычислений. В случае критерия Никулина можно воспользоваться или
асимптотически оптимальным группированием или разбиением на интервалы равных
вероятностей.
В-третьих, на выбор числа интервалов. Выбор слишком большого числа
интервалов приводит к падению мощности. Оптимальное число интервалов ![]() зависит от объема выборки
зависит от объема выборки ![]() и от конкретной пары конкурирующих
гипотез
и от конкретной пары конкурирующих
гипотез ![]() и
и ![]() . Чаще всего оптимальное
. Чаще всего оптимальное ![]() оказывается существенно
меньше значений, рекомендуемых различными регламентирующими документами и задаваемых
множеством эмпирических формул, представленных в [16]. Максимальная мощность
критериев при заданном объеме выборки
оказывается существенно
меньше значений, рекомендуемых различными регламентирующими документами и задаваемых
множеством эмпирических формул, представленных в [16]. Максимальная мощность
критериев при заданном объеме выборки ![]() часто
достигается при минимально возможном или достаточно малом числе интервалов
часто
достигается при минимально возможном или достаточно малом числе интервалов ![]() (см. рис. 3-4). Если Вас интересует конкретная пара альтернатив, относительно
которых часто приходится принимать решение, воспользуйтесь соотношением (5) для
подбора оптимального числа интервалов
(см. рис. 3-4). Если Вас интересует конкретная пара альтернатив, относительно
которых часто приходится принимать решение, воспользуйтесь соотношением (5) для
подбора оптимального числа интервалов ![]() при
заданном объеме выборки
при
заданном объеме выборки ![]() . Если это окажется затруднительным, можно при выборе числа
интервалов опираться на таблицы асимптотически оптимального группирования
[11, 23, 25], выбирая
. Если это окажется затруднительным, можно при выборе числа
интервалов опираться на таблицы асимптотически оптимального группирования
[11, 23, 25], выбирая ![]() таким образом, чтобы ожидаемое число наблюдений,
попадающих в любой интервал при асимптотически оптимальном группировании, было
не очень малым:
таким образом, чтобы ожидаемое число наблюдений,
попадающих в любой интервал при асимптотически оптимальном группировании, было
не очень малым: ![]() .
Как показывает практика, в этом случае число
.
Как показывает практика, в этом случае число ![]() обычно оказывается близким
к оптимальному.
обычно оказывается близким
к оптимальному.
Выполнив первое условие, мы будем иметь возможность точно вычислять
значение критерия, соответствующее задаваемой величине вероятности ошибки
первого рода ![]() (или
вычислять достигаемый уровень значимости по предельному распределению
статистики
(или
вычислять достигаемый уровень значимости по предельному распределению
статистики ![]() ).
Выбрав же оптимальное число интервалов и подобрав
оптимальное разбиение на интервалы, мы получим критерий максимальной мощности,
наилучшим образом различающий конкретные конкурирующие гипотезы (обеспечивающий
минимальную вероятность ошибки второго рода
).
Выбрав же оптимальное число интервалов и подобрав
оптимальное разбиение на интервалы, мы получим критерий максимальной мощности,
наилучшим образом различающий конкретные конкурирующие гипотезы (обеспечивающий
минимальную вероятность ошибки второго рода ![]() при заданной вероятности
ошибки первого рода
при заданной вероятности
ошибки первого рода ![]() ).
).
В заключение отметим, что техническим комитетом ТК 125
“Стандартизация статистических методов управления качеством” готовятся на
утверждение Госстандартом РФ методические рекомендации по применению критериев
типа ![]() ,
подготовленные на базе [23] и последних результатов.
,
подготовленные на базе [23] и последних результатов.
1. Кендалл М., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973. – 900 с.
2. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.
3. Birch M.W. A new proof of the Pearson–Fisher theorem // Ann. Math. Statist. – 1964. V. 35. – P. 817.
4. Сархан А.Е., Гринберг Б.Г. Введение в теорию порядковых статистик. – М.: Статистика, 1970. – 414 с.
5. Лемешко Б.Ю. Оптимальные оценки параметров сдвига и масштаба по выборочным квантилям для больших выборок / Тр. третьей международной научно-технической конференциии “Актуальные проблемы электронного приборостроения АПЭП-96”. – Т. 6. – Ч.1. – Новосибирск, 1996. – С. 37-44
6. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. – Новосибирск: Изд-во НГТУ, 1995. – 125 с.
7. Лемешко Б.Ю., Постовалов С.Н. Объектно-ориентированная версия программной системы статистического анализа // Материалы международной НТК "Информатика и проблемы телекоммуникаций". – Новосибирск, 1998. – С. 98-99.
8. Лемешко Б.Ю., Постовалов С.Н. Система статистического анализа наблюдений и исследования статистических закономерностей // Материалы международной НТК "Информатика и проблемы телекоммуникаций". – Новосибирск, 2001. – С. 80-81.
9. Рао. С.Р. Линейные статистические методы и их применения. – М.: Наука, 1968. – 548 с.
10.
Лемешко Б.Ю., Постовалов С.Н. О зависимости предельных распределений
статистик ![]() Пирсона и отношения правдоподобия от способа
группирования данных // Заводская лаборатория. 1998. – Т. 64. – № 5. – С.56-63.
Пирсона и отношения правдоподобия от способа
группирования данных // Заводская лаборатория. 1998. – Т. 64. – № 5. – С.56-63.
11. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов. В 2-х ч. / Новосиб. гос. техн. ун-т. – Новосибирск, 1993. – 347 с.
12. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев // Надежность и контроль качества. 1997. – № 8. – С. 3-14.
13. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория. 1998. – Т. 64. – №1. – С.56-64.
14. Левин Б.Р. Теория надежности радиотехнических систем (математические основы). – М.: Сов. Радио, 1978. – 264 с.
15. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Юнити, 2000. – 543 с.
16. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л.: Энергоатомиздат, 1991. – 303 с.
17. Никулин М.С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и её применение. 1973. – Т.XVIII. – № 3. – С.675-676.
18. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. – Т. XVIII. – № 3. – С.583-591.
19.
Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // Заводская лаборатория. 1992. – Т. 58. – № 3. – С.52-58.
20. Aguirre N., Nikulin M. Chi-squared goodness-of-fit test for the family of logistic distributions // Kybernetika. 1994. V. 30. – № 3. – P.214-222.
21.
Лемешко Б.Ю., Постовалов С.Н., Чимитова
Е.В. О распределениях статистики и мощности критерия типа ![]() Никулина // Заводская лаборатория. Диагностика
материалов. 2001. – Т. 67. – № 3. – С. 52-58.
Никулина // Заводская лаборатория. Диагностика
материалов. 2001. – Т. 67. – № 3. – С. 52-58.
22. Денисов В.И., Лемешко Б.Ю. Оптимальное группирование при обработке экспериментальных данных // Измерительные информационные системы. – Новосибирск, 1979. – С. 5-14.
23.
Денисов В.И., Лемешко
Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия
опытного распределения с теоретическим. Методические
рекомендации. Часть I. Критерии типа ![]() . – Новосибирск: Изд-во НГТУ, 1998. – 126 с.
. – Новосибирск: Изд-во НГТУ, 1998. – 126 с.
24. Кендалл М., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973. – 900 с.
25. http://www.ami.nstu.ru/~headrd/applied/index.html.
26. Чибисов Д.М., Гванцеладзе Л.Г. О критериях согласия, основанных на группированных данных // III советско-японский симпозиум по теории вероятностей. Ташкент: изд-во “Фан”, 1975. – С. 183-185.
27.
Боровков А.А. О мощности критерия ![]() при увеличении числа групп // Теория вероятностей
и ее применение. 1977. – Т. XXII. – № 2. – С.375-378.
при увеличении числа групп // Теория вероятностей
и ее применение. 1977. – Т. XXII. – № 2. – С.375-378.
28.
Лемешко Б.Ю., Чимитова Е.В.
Максимизация мощности критериев типа ![]() //
Доклады Сибирского отделения Академии наук высшей школы. Новосибирск, 2000. – №
2. – С. 53-61.
//
Доклады Сибирского отделения Академии наук высшей школы. Новосибирск, 2000. – №
2. – С. 53-61.
29. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
[1] Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 00-01-00913)