См. также: Прикладная математическая статистика (материалы к семинарам)

Надежность и контроль качества. - 1997. - № 8. - С. 3-14.

УДК 519.2

Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев согласия

Лемешко Б.Ю

Показывается, что асимптотически оптимальное группирование наблюдений обеспечивает при близких альтернативах максимальную мощность критериев согласия  Пирсона и отношения правдоподобия. Использование полученных таблиц оптимального группирования сокращает риск необоснованного принятия гипотез о согласии.

            Ни для кого не секрет, что результаты проверки гипотез о согласии в соответствии с критерием  Пирсона существенно зависят от того, как сгруппированы данные: сгруппировали одним способом, гипотезу о согласии можно принять, сгруппировали другим - гипотеза о согласии должна быть отвергнута. Откуда же взять уверенность в таком выводе?

Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой мы наблюдали. Поэтому, после того как вычислены оценки параметров гипотетического распределения, необходимо проверить, насколько хорошо выборка согласуется с найденным законом. Такие проверки осуществляются с использованием различных критериев согласия.

            Проверка гипотезы вида , где  - оценка параметра распределения, осуществляется по следующей схеме. Для выбранного критерия вычисляется значение  статистики  как некоторой функции от выборки и закона распределения . Для используемых на практике критериев обычно известны асмиптотические (предельные) распределения  соответствующих статистик при условии истинности гипотезы . Далее в принятой практике статистического анализа обычно сравнивают полученное значение статистики  с критическим  для данного уровня значимости  и нулевую гипотезу отвергают, если . Критическое значение , определяемое из уравнения

,

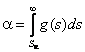обычно берётся из соответствующей статистической таблицы.

            Естественно, что больше информации о степени согласия можно почерпнуть из величины вероятности превышения полученного значения статистики при истинности нулевой гипотезы 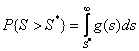. Именно она позволяет судить о степени согласия, так как по существу представляет собой вероятность истинности нулевой гипотезы. Гипотеза о согласии не отвергается, если .

            Задачи оценивания параметров и проверки гипотез опираются на выборки независимых случайных величин. Случайность самой выборки предопределяет, что возможны и ошибки в результатах статистических выводов. С результатами проверки гипотез связывают ошибки 2 видов: ошибка 1-го рода состоит в том, что отклоняется гипотеза , когда она верна; ошибка 2-го рода состоит в том, что принимается гипотеза , в то время как справедлива альтернативная гипотеза . Величина  задаёт вероятность ошибки 1-го рода. Если гипотеза  определена, то задание  определяет и вероятность ошибки 2-го рода  для используемого критерия проверки гипотез. На рис. 1  отображает плотность распределения статистики  при истинности гипотезы , а  - плотность распределения при справедливости гипотезы .

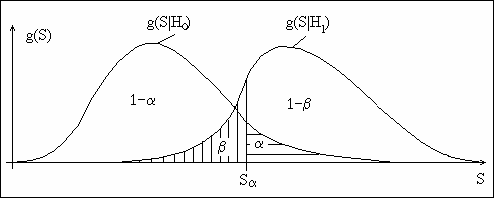
Рис. 1. Распределения статистик при справедливости гипотез  и

            Мощность критерия представляет собой величину . Понятно, что чем выше мощность используемого критерия при заданном значении , тем лучше он различает гипотезы  и . Особенно важно, чтобы используемый критерий хорошо различал близкие альтернативы. Графически требование максимальной мощности критерия означает, что на рис. 1 плотности  и  должны быть максимально "раздвинуты".

В [1] отмечается, что искать оптимальный метод определения границ интервалов для критерия  следует в терминах мощности критерия, т.е. выбирать такую совокупность границ, которая максимизировала бы мощность критерия данного размера. Правило использования интервалов равной вероятности предложено Манном и Вальдом в 1942 г. При таком разбиении максимизируется энтропия, равная  [2]. В этом случае максимизируется асимптотическая мощность критерия, если не требуется рассматривать какую-либо конкретную альтернативу.

Фишеровская информация служит мерой внутренней близости распределений случайных величин, и этот внутренний характер связан с мощностью различения между близкими значениями параметра [3]. Статистика редуцирует выборочные данные, и поэтому мощность различения с помощью статистики не больше, чем с помощью всей выборки. А это значит, если нужно выбирать между несколькими статистиками, следует предпочесть ту, для которой потери фишеровской информации минимальны.

            Статистика критерия согласия  Пирсона, вычисляемая в соответствии с соотношением

,

где  - вероятность попадания наблюдения в -й интервал, при истинной гипотезе  в пределе подчиняется -распределению с числом степеней свободы , если по выборке не оценивались параметры, и с , если по ней оценивалось  параметров закона распределения.

            Эта же статистика подчиняется нецентральному -распределению с тем же числом степеней свободы и параметром нецентральности

,

если верна конкурирующая гипотеза и выборка соответствует распределению того же типа, но с параметром  (в общем случае векторным). Мощность критерия  Пирсона является неубывающей функцией от . Несложно показать [4-5], разлагая в ряд Тейлора при малых  и пренебрегая членами высшего порядка, что

,

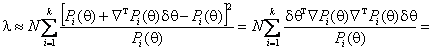
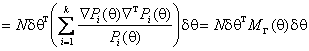где  - информационная матрица Фишера вектора параметров распределения по группированным наблюдениям. Таким образом, чем меньше потери информации, вызванные группированием, то есть чем ближе к информационная матрица Фишера по негруппированным наблюдениям , тем выше мощность критерия  Пирсона при близких альтернативах. Выбирая граничные точки так, чтобы  стремилась к информационной матрице по негруппированным данным , мы обеспечиваем максимальную мощность критерия.

            Аналогичный результат справедлив для критерия отношения правдоподобия [5]. В этом критерии согласия используется статистика вида [1]

.

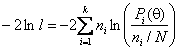При верной нулевой гипотезе она асимптотически распределена как  с -й степенью свободы. Если по выборке оценивались параметры распределения, то число степеней свободы уменьшается на количество оцененных параметров.

            Решение задачи асимптотически оптимального группирования в скалярном случае заключается в максимизации количества информации Фишера о параметре, а в векторном - в максимизации некоторого функционала от информационной матрицы Фишера по группированным данным.

            Приемы группирования, в основном применяемые на практике: разбиение области, в которую попали выборочные значения случайной величины, на интервалы равной длины или на интервалы равной вероятности, - в общем случае весьма далеки от оптимального. Проведенные численные исследования по сравнению способов группировки данных показали неоспоримое преимущество асимптотически оптимального группирования.

            Информационная матрица Фишера зависит от параметров исследуемого распределения. Однако для достаточно широкого ряда распределений при решении задач асимптотически оптимального группирования удалось получить граничные точки интервалов в виде, инвариантном относительно параметров распределений, и на их основе сформировать таблицы асимптотически оптимального группирования. Наиболее полная совокупность таблиц асимптотически оптимального группирования для распределений экспоненциального, полунормального, Рэлея, Максвелла, модуля многомерного нормального вектора, Парето, Эрланга, Лапласа, нормального, логарифмически-нормальных (ln и lg), Коши, Вейбулла, распределений минимального и максимального значения, двойного показательного, гамма-распределения представлена в [5]. В общей сложности получено 54 таблицы оптимальных граничных точек и соответствующих вероятностей. Эти таблицы могут использоваться как при оценивании, так и при проверке гипотез. Полученные таблицы используются в программной системе [6] при проверке согласия по критериям  Пирсона и отношения правдоподобия и при вычислении робастных оценок. В качестве примера в табл. 1 представлены асимптотически оптимальные граничные точки для проверки согласия с нормальным распределением.

            Для многих законов распределений граничные точки интервалов не могут быть выражены в виде, инвариантном относительно параметров распределений, т.е. они остаются функциями этих параметров. Это касается, например, таких законов, как гамма- и бета-распределения [7,8], экспоненциального семейства распределений. В этом случае формирование таблиц асимптотически оптимального группирования теряет смысл. Однако возможно решение задачи асимптотически оптимального группирования при конкретных значениях параметров в процессе проверки гипотез о согласии, как это реализуется в таких ситуациях в программной системе [6].

            На рис. 2 проведено сравнение функций мощности критерия  Пирсона при проверке согласия с распределением Вейбулла, когда по выборке оценивался основной параметр (формы). Функции мощности построены в зависимости от величины отклонения от значения параметра , соответствующего гипотезе . Выбор в качестве объекта сравнения случая равновероятного группирования обоснован определённостью этой процедуры разбиения и ее оптимальностью при отсутствии конкретных альтернатив [2].

Таблица 1.

Оптимальные граничные точки интервалов в виде  при одновременном оценивании двух параметров нормального распределения и при проверке гипотез о согласии по критериям  Пирсона и отношения правдоподобия и соответствующие значения относительной асимптотической информации

3	-1.1106	1.1106
4	-1.3834	0.0	1.3834
5	-1.6961	-0.6894	0.6894	1.6961
6	-1.8817	-0.9970	0.0	0.9970	1.8817
7	-2.0600	-1.2647	-0.4918	0.4918	1.2647	2.0600
8	-2.1954	-1.4552	-0.7863	0.0	0.7863	1.4552	2.1954
9	-2.3188	-1.6218	-1.0223	-0.3828	0.3828	1.0223	1.6218
10	-2.4225	-1.7578	-1.2046	-0.6497	0.0	0.6497	1.2046
11	-2.5167	-1.8784	-1.3602	-0.8621	-0.3143	0.3143	0.8621
12	-2.5993	-1.9028	-1.4914	-1.0331	-0.5334	0.0	0.5334
13	-2.6746	-2.0762	-1.6068	-1.1784	-0.7465	-0.2669	0.2669
14	-2.7436	-2.1609	-1.7092	-1.3042	-0.9065	-0.4818	0.0
15	-2.8069	-2.2378	-1.8011	-1.4150	-1.0435	-0.6590	-0.2325

							0.4065
							0.5527
							0.6826
							0.7557
							0.8103
							0.8474
2.3188							0.8753
1.7578	2.4225						0.8960
1.3602	1.8784	2.5167					0.9121
1.0331	1.4914	1.9028	2.5993				0.9247
0.7465	1.1784	1.6068	2.0762	2.6746			0.9348
0.4818	0.9065	1.3042	1.7092	2.1609	2.7436		0.9430
0.2325	0.6590	1.0435	1.4150	1.8011	2.2378	2.8069	0.9498

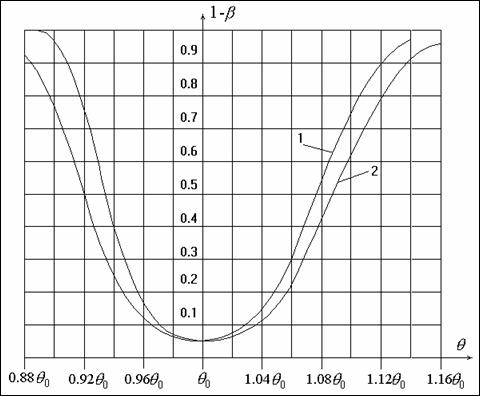
Рис. 2. Функция мощности критерия  Пирсона при проверке гипотез об основном (формы) параметре распределения Вейбулла: уровень значимости , объем выборки , количество интервалов ; 1 - для оптимального группирования; 2 - для равновероятного группирования.

            Все приводимые в дальнейшем результаты и иллюстрации получены с использованием программной системы [6]. Продемонстрируем, как отражается соответствующий способ группирования на результатах проверки гипотез о согласии. С этой целью была смоделирована выборка объёмом 1000 наблюдений в соответствии с логистическим распределением с плотностью

.

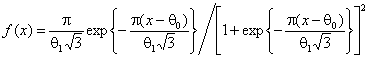При моделировании были заданы параметры: . Это закон отличается от нормального несколько более тяжелыми хвостами. Результаты моделирования представлены на рис. 3.

            На этом и последующем аналогичных рисунках приведены значения статистик отношения правдоподобия,  Пирсона, Колмогорова, Смирнова,  и Мизеса, вычисляемые при проверке гипотез о согласии, и соответствующие вероятности вида , где  - вычисленное значение соответствующей статистики. Гипотеза о согласии не отвергается, если , где  - заданный уровень значимости. Для статистик отношения правдоподобия и  Пирсона значения вероятностей приводятся при двух различных степенях свободы (в скобках). Разность степеней свободы определяется количеством параметров, оцененных по выборке. Полученные по смоделированной выборке оценки максимального правдоподобия (ОМП) параметров логистического распределения , . При проверки согласия по критериям отношения правдоподобия и  Пирсона использовано асимптотически оптимальное группирование. Как видим по значениям статистик и соответствующим вероятностям, согласие по всем критериям очень хорошее.

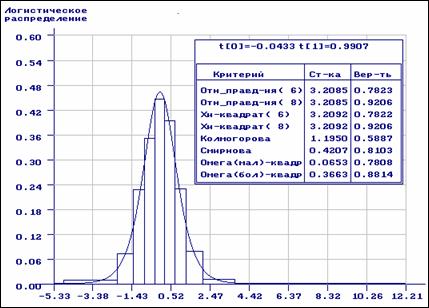
Рис. 3. Результаты статистического анализа для логистического распределения

            Допустим, у нас возникла потребность описать данную выборку с помощью нормального распределения. На рис. 4 представлены результаты выравнивания в соответствии с нормальным законом. Найденные ОМП параметров нормального распределения , . При проверке согласия по критериям отношения правдоподобия и  Пирсона использовалось равновероятное группирование. Если обратим внимание на результаты проверки гипотез о согласии, то увидим, что при уровне значимости  у нас нет оснований отклонять гипотезу о нормальности по критериям  Пирсона и отношения правдоподобия.

            ОМП подвержены влиянию грубых ошибок и отклонений от вида предполагаемого распределения. Так как выборка моделировалась в соответствии с логистическим распределением, то, естественно, это повлияло на оценки параметров нормального распределения. На рис. 5. представлены аналогичные результаты, но в данном случае были найдены робастные ОМП параметров по группированным данным. И при оценивании, и при проверке согласия выборка разбивалась на равновероятные интервалы. ОМП параметров нормального распределения по группированным данным , . Как видим, достаточно хорошее согласие: если уровень значимости , то по всем критериям, кроме Мизеса, гипотеза о согласии будет принята! Эмпирическая и полученная теоретическая функция распределения нормального закона визуально имеют некоторое расхождение на хвостах, но с точки зрения практически всех используемых критериев это расхождение незначимо.

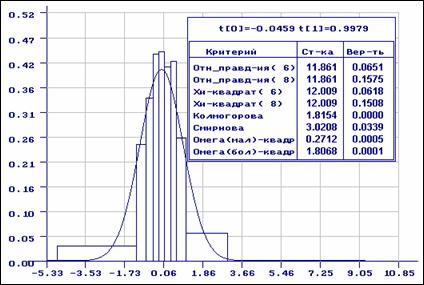
Рис. 4. Выравнивание в соответствии с нормальным законом ОМП найдены по негруппированным данным; при проверке согласия использовано равновероятное группирование

            Результаты статистического анализа, представленные на рис. 6, отличаются от предыдущего случая тем, что в критериях согласия отношения правдоподобия и  Пирсона использовалось асимптотически оптимальное группирование. Сравните значения статистик отношения правдоподобия и  Пирсона с их значениями, представленными на рис. 5. Гипотеза о согласии в данном случае будет отклоняться при  по критерию отношения правдоподобия и при  по критерию  Пирсона.

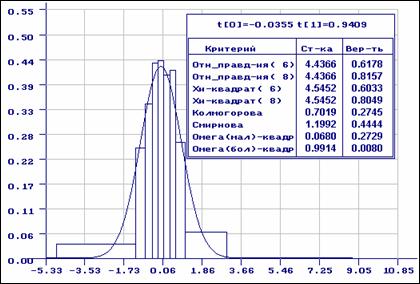
Рис. 5. Выравнивание в соответствии с нормальным законом:

ОМП найдены по группированным данным; при оценивании

и при проверке согласия использовано равновероятное

группирование

            Из приведенных примеров и всего вышесказанного должно быть очевидно, что применение асимптотически оптимального группирования в критериях согласия снижает риск необоснованного принятия гипотез о согласии. Если нас действительно интересует, насколько сильно отличается выборка от предполагаемого распределения, следует применять критерии отношения правдоподобия и  Пирсона с использованием асимптотически оптимального группирования, что гарантирует их максимальную мощность при распознавании близких гипотез.

            В рассмотренных на рис. 4-6 примерах при использовании критериев типа Колмогорова, Смирнова,  и Мизеса при вычислении вероятности вида  учитывался факт оценивания по выборке параметров распределения. Известно, что в этом случае предельные распределения статистик этих критериев зависят как от вида рассматриваемого закона, так и от числа оцененных параметров. Искомые вероятности вычислялись в соответствии с моделями предельных распределений статистик, полученными в [9].

            Все упоминаемые в данной работе критерии используют различные меры близости распределений, по разному улавливают различные отклонения. Поэтому для надежности статистических выводов не следует останавливаться на применении какого-то одного критерия.

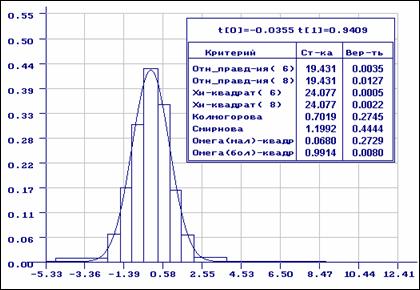
Рис. 6. Выравнивание в соответствии с нормальным законом: ОМП найдены по группированным данным; при проверке согласия использовано асимптотически оптимальное группирование

            Достаточно часто используемые критерии не позволяют отклонить гипотезу о согласии с одним распределением, с другим, с третьим ... Особенно это характерно для ограниченных объёмов выборок, зачастую встречающихся на практике. Если мы стремимся подобрать модель, которая наиболее хорошо описывает выборочные наблюдения, нельзя доверять выводам типа “с уровнем значимости таким-то гипотеза о согласии с нормальным распределением не отвергается”, так как наверняка с большим основанием не будет отвергаться гипотеза о согласии и с другими распределениями.

1. Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.

2. Кокс Д., Хинкли Д. Теоретическая статистика. - М.: Мир, 1978. - 560 с.

3. Рао. С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968. - 548 с.

4. Денисов В.И., Лемешко Б.Ю. Оптимальное группирование при обработке экспериментальных данных // Измерительные информационные системы. - Новосибирск, 1979. - С. 5-14.

5. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов. В 2-х ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. - 347 с.

6. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. - Новосибирск: Изд-во НГТУ,  1995. - 125 с.

7. Денисов В.И., Зачепа Г.Г., Лемешко Б.Ю. Об асимптотически оптимальном группировании при оценивании основного параметра гамма-распределения по группированным данным // Применение ЭВМ в оптимальном планировании и проектировании. - Новосибирск, 1974. - С. 50-53.

8. Лемешко Б.Ю. К вопросу решения задачи асимптотически оптимального группирования данных при обработке наблюдений, подчиняющихся бета-распределению // Машинные методы оптимизации, моделирования и планирования эксперимента. - Новосибирск, 1988. - С. 134-138.

9. Лемешко Б.Ю., Постовалов С.Н. К вопросу о распределениях статистик непараметрических критериев согласия // Сб. научных трудов НГТУ. - 1997. - № 1(6). - С. 23-32.

[Содержание]