См. также: Прикладная
математическая статистика (материалы к семинарам)
Надежность и контроль качества. - 1997. - № 11. - С. 3-17.
УДК 519.2
Прикладные аспекты использования критериев согласия в случае проверки сложных гипотез
Б.Ю. Лемешко, С.Н. Постовалов
При исследовании надежности и контроля качества часто возникает необходимость идентификации закона распределения вероятностей, наиболее адекватно описывающего наблюдаемую случайную величину. В этой связи обычно последовательно решают две задачи: сначала оценивают параметры закона распределения, выбор которого определяется некоторыми теоретическими или практическими соображениями, а затем с использованием какого-либо критерия (или критериев) согласия проверяется гипотеза о принадлежности наблюдаемой выборки найденному закону. При этом наиболее часто проверка согласия осуществляется по той же самой выборке, по которой вычислялись оценки параметров. Именно в этот момент совершается большинство непреднамеренных или преднамеренных ошибок проводимого статистического анализа.
В рассматриваемой ситуации при проверке согласия нулевая гипотеза имеет вид 
,
где 
- плотность распределения наблюдаемого закона,
- истинное значение параметра, 
- оценка параметра, вычисленная по выборке.
С каждым критерием согласия связана определенная статистика 
, вычисляемая по выборке, для которой должен быть
известен предельный закон распределения при истинной нулевой гипотезе 
. Если вероятность 
, вычисленная в соответствии с этим предельным
законом, где 
- полученное по выборке значение статистики, не
меньше задаваемого уровня значимости 
,
то гипотеза 
принимается. Проблема связана с тем, что
предельные распределения статистик в случаях проверки простой и сложной
гипотез обычно кардинально отличаются. Например, предельные распределения
статистик непараметрических критериев согласия типа Колмогорова, Смирнова или 
и 
Мизеса
при оценивании по данной выборке параметров зависят как от вида наблюдаемого
закона, так и от количества, и типа оцениваемых параметров, а иногда и от
конкретного значения параметра.
В критериях согласия 
Пирсона
или отношения правдоподобия, статистики
и [1]
,
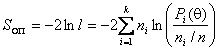где
- объем выборки, 
– количество наблюдений, попавших в интервал, 
- вероятность попадания наблюдения в 
-й интервал, в случае простой гипотезы подчиняются
распределению 
(с числом степеней свободы 
, где 
-
число интервалов, на которые разбивается выборка). При проверке сложной
гипотезы и оценивании по выборке параметров изменение закона распределения статистик учитывается уменьшением числа степеней свободы
предельного распределения на число 
оцененных
по выборке параметров (
)
[1]. Последнее справедливо только в случае, если оценки параметров вычисляются
по группированной выборке. Если же находятся, например, оценки максимального
правдоподобия по негруппированным данным, то предельные распределения этих
статистик лежат между и
и зависят от вида
оцениваемого параметра, и даже способа группирования [2]. Поэтому надо
учитывать, что при использовании в такой ситуации в качестве предельного
закона вычисляемые вероятности 
обычно оказываются заниженными (увеличивается
вероятность ошибки первого рода: отклонить верную гипотезу ).
Проведенное нами сравнительное исследование влияния способов
группирования (равновероятного и асимптотически оптимального, при котором
минимизируются потери в количестве информации Фишера [3,4]) на предельные
законы статистик этих критериев показало, что если по наблюдаемой выборке не
оценивались параметры закона, то распределения статистик критериев отношения
правдоподобия и 
Пирсона при справедливой гипотезе достаточно хорошо согласуются
с как при равновероятном, так и
при асимптотически оптимальном группировании. Различия между распределениями статистик при
равновероятном и асимптотически оптимальном группировании заметны, но не
значимы. При этом распределения статистик при равновероятном группировании в
целом оказываются ближе к распределению.
При проверке сложных гипотез, когда оценки параметров определяются по
негруппированным наблюдениям, предельные распределения статистик критериев
отношения правдоподобия и Пирсона
существенно зависят от способа группирования (и вида закона), особенно при
малом числе интервалов. При этом распределения статистик зависят не только от
количества оцененных по выборке параметров, но и от того, какой параметр
оценивался. Оценивание параметра сдвига приводит к более значительному
изменению распределений статистик, чем оценивание масштабного параметра.
В целом, при малом числе интервалов и оценивании параметров число степеней свободы предельного
распределения уменьшается на “число степеней свободы” меньшее . При этом предельный закон распределения статистики
при асимптотически оптимальном группировании ближе к теоретическому -распределению, чем при равновероятном группировании.
На рис. 1 приведены результаты моделирования распределений статистики Пирсона при 7 интервалах и оценивании двух параметров
нормального распределения при справедливой гипотезе . На рисунке построены функции распределения при 4, 5 и 6 степенях свободы и эмпирические
функции распределения статистики Пирсона
при асимптотически оптимальном (“1”) и равновероятном (“2”) группировании.
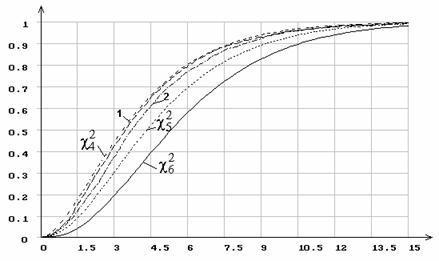
Рис. 1. Распределения статистики Пирсона при 7 интервалах и оценивании двух
параметров нормального распределения
Расчеты показали, что при использовании для вычисления 
функции распределения при асимптотически оптимальном группировании и
малом числе интервалов (
) при малых (именно
при малых вероятностях принимается решение отклонить гипотезу или нет) погрешность имеет величины, которые не
существенны для практических задач. То есть в этом случае, используя , мы не совершаем большой ошибки.
С ростом числа интервалов (при
соответствующем объеме выборки) отличие предельных распределений статистик от
распределений и при асимптотически оптимальном, и при
равновероятном группировании становится несущественным. При этом разность между
функцией распределения и
действительными функциями распределения статистик отношения правдоподобия и
Пирсона в случае асимптотически оптимального
группирования убывает существенно быстрее.
Распределения данных статистик при справедливой конкурирующей гипотезе 
всегда (и с оцениванием параметров и без
оценивания) сильно зависят от варианта группирования. Разность –
при близких альтернативах и асимптотически оптимальном группировании максимальна
и, следовательно, максимальна мощность критерия.
Непараметрические критерии типа Колмогорова, Смирнова, и Мизеса при оценивании по
выборке параметров теряют свойство “свободы от распределения”, и предельные
распределения статистик этих критериев становятся зависящими как от числа
оцененных параметров, так и от вида исследуемого закона распределения 
. Хотя эта проблема приобрела
широкую известность с выходом работы [5], ещё достаточно часто она не
учитывается при использовании этих критериев на практике, что можно объяснить лишь недостаточной освещенностью этих
вопросов в учебной и справочной литературе. О недопустимости пренебрежения фактом
зависимости распределений статистик непараметрических критериев от
оценивания параметров предупреждается в работах [6,7], где подчеркивается,
что это приводит к необоснованному принятию нулевой гипотезы из-за сильно завышенных
значений вероятностей “согласия” вида .
При большом объеме выборки можно, опираясь на результаты, полученные в [8], оценивать параметры распределения по одной половине выборки, а проверять согласие по другой половине. В такой ситуации применение предельных распределений рассматриваемых классических критериев вполне обосновано. Но объемы выборок, зачастую имеющиеся в распоряжении исследователя, не настолько велики, чтобы можно было смириться еще и с разбиением ее на две отдельные части.
Для случая нормального закона предельные распределения статистики критерия Мизеса при оценивании одного из двух или обоих
параметров подробно исследованы и табулированы в [9].
Теоретически решить задачу определения предельных распределений непараметрических статистик для множества законов, используемых для описания наблюдаемых величин, не реально. Поэтому большинство существующих таблиц процентных точек для предельных распределений получены методом статистического моделирования [10-13].
В работах [14-17] для статистик типа Колмогорова-Смирнова
получены формулы для приближенного вычисления вероятностей вида . С помощью этих формул,
учитывающих отличие предельных распределений непараметрических
статистик при оценивании параметров законов от классических, вычисляют
вероятности вида в пакете STADIA [18].
Нами в результате моделирования предельных законов распределения статистик непараметрических критериев найдены такие законы распределения вероятностей, которые с практической точки зрения хорошо аппроксимируют предельные распределения статистик непараметрических критериев в тех случаях, когда по выборке оцениваются параметры [19].
Полученные результаты могут с успехом применяться при решении практических задач проверки гипотез о согласии с использованием непараметрических критериев после вычисления оценок параметров распределения по той же выборке.
В данной работе статистики всех непараметрических критериев рассматриваются в том виде, как они даны в [20]. Статистика Колмогорова определяется выражением
,
статистика Смирнова
,
где
-
объем выборки, 
- упорядоченные по возрастанию выборочные
значения, 
- функция распределения, согласие с которой проверяется.
Распределение величины 
,
если по выборке не оценивались параметры, в пределе подчиняется закону Колмогорова
с функцией распределения 
[20].
В аналогичной ситуации статистика Смирнова 
подчиняется
в пределе распределению с
числом степеней свободы, равным 2 [20].
Статистики Мизеса имеют вид
(статистика Крамера-Мизеса-Смирнова) и
(статистика Андерсона-Дарлинга). Для этих статистик также известны предельные распределения вероятностей [20]
, 
.
Результаты моделирования и последующего анализа с использованием программной
системы [21] показали, что законы распределения статистик непараметрических
критериев достаточно хорошо описываются одним из двух законов распределения:
логарифмически нормальным или гамма-распределением.
Исследованы распределения непараметрических статистик,
когда наблюдаемые случайные величины распределены в соответствии с законами:
экспоненциальным, с плотностью 
; полунормальным - 
; Рэлея - 
; Максвелла - 
; Лапласа - 
; нормальным - 
; логнормальным - 
; Коши - 
; наибольшего и наименьшего значения
- 
и 
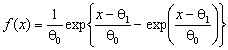; Вейбулла-Гнеденко - 
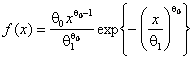; логистическим - 
.
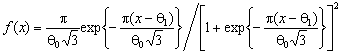В табл. 1 приведены указания на конкретные распределения, которые лучше всего описывают эмпирические распределения статистики критерия Колмогорова (согласуются).
Таблица 1.
|
Предельные распределения статистики Колмогорова |
||||
|
№ п/п |
Распределение случайной величины |
Оценивался только масштабный параметр |
Оценивался только параметр сдвига |
Оценивалось два параметра |
|
1. |
Экспоненциальное |
lnN(-0.3477,0.2638) |
|
|
|
2. |
Полунормальное |
g(3.4090,8.2385,0.3443) |
|
|
|
3. |
Рэлея |
lnN(-0.3366,0.2579) |
|
|
|
4. |
Максвелла |
g(3.4809,9.0801,0.3417) |
|
|
|
5. |
Лапласа |
g(3.2121,6.5137,0.3400) |
lnN(-0.3721,0.2426) |
lnN(-0.4679,0.2329) |
|
6. |
Нормальное |
g(3.6448,7.0208,0.3164) |
lnN(-0.4349,0.2337) |
lnN(-0.4849,0.2254) |
|
7. |
Логнормальное |
g(3.7326,7.4146,0.3265) |
g(3.0857,8.4464,0.3532) |
g(3.7311,10.045,0.3062) |
|
8. |
Коши |
g(3.1388,6.7500,0.3261) |
lnN(-0.3691,0.2542) |
g(4.2049,13.595,0.2983) |
|
9. |
Логистическое |
g(3.3283,6.6563,0.3280) |
lnN(-0.4681,0.2248) |
lnN(-0.5684,0.2111) |
|
10. |
Экстремальных значений (min и max) и Вейбулла |
lnN(-0.2243,0.3028) |
lnN(-0.3505,0.2652)** |
lnN(-0.4996,0.2221) |
** - оценивался параметр формы распределения Вейбулла.
В этой и последующих таблицах 
соответствует
логарифмически нормальному распределению с функцией плотности
,
- гамма-распределению с
функцией плотности
.
В
случае если согласие с каким-то законом не очень хорошее (гипотеза о согласии
принимается с уровнем значимости 
),
то соответствующий закон указан на сером фоне.
В табл. 2-4 приведены соответственно законы распределения статистик Смирнова, и Мизеса
при оценивании различных параметров наблюдаемого закона.
Таблица 2.
|
Предельные распределения статистики Смирнова |
||||
|
№ п/п |
Распределение случайной величины |
Оценивался только масштабный параметр |
Оценивался только параметр сдвига |
Оценивалось два параметра |
|
1. |
Экспоненциальное |
lnN(0.1585,0.7009) |
|
|
|
2. |
Полунормальное |
lnN(0.1289,0.7900) |
|
|
|
3. |
Рэлея |
lnN(0.1936,0.7073) |
|
|
|
4. |
Максвелла |
lnN(0.2221,0.6794) |
|
|
|
5. |
Лапласа |
g(0.8146,0.4654,0.0006) |
g(1.7664,1.2256,0.0207) |
g(1.8235,1.5842,0.0058) |
|
6. |
Нормальное |
g(0.8088,0.4549,0.0006) |
lnN(0.2471,0.5321) |
lnN(0.1299,0.5331) |
|
7. |
Логнормальное |
g(0.8391,0.4641,0.0006) |
lnN(0.4252,0.6481) |
lnN(0.1947,0.6783) |
|
8. |
Коши |
g(0.8570,0.5348,0.0006) |
g(1.4215,0.9846,0.0006) |
g(1.2931,1.2542,0.0006) |
|
9. |
Логистическое |
g(0.8164,0.4709,0.0) |
lnN(0.2684,0.4856) |
lnN(0.0569,0.4491) |
|
10. |
Экстремальных значений (min и max) и Вейбулла |
g(0.8372,0.4637,0.0006) |
lnN(0.2040,0.7135)** |
lnN(0.1151,0.5065) |
** - оценивался параметр формы распределения Вейбулла.
Таблица 3.
|
Предельные распределения статистики |
||||
|
№ п/п |
Распределение случайной величины |
Оценивался только масштабный параметр |
Оценивался только параметр сдвига |
Оценивалось два параметра |
|
1. |
Экспоненциальное |
lnN(-2.6028,0.6453) |
|
|
|
2. |
Полунормальное |
lnN(-2.5046,0.6814) |
|
|
|
3. |
Рэлея |
lnN(-2.5743,0.6345) |
|
|
|
4. |
Максвелла |
lnN(-2.6147,0.6361) |
|
|
|
5. |
Лапласа |
lnN(-2.2328,0.8302) |
lnN(-2.6890,0.5802) |
lnN(-2.9386,0.5500) |
|
6. |
Нормальное |
lnN(-2.2290,0.8284) |
lnN(-2.8102,0.5625) |
lnN(-2.9685,0.5187) |
|
7. |
Логнормальное |
lnN(-2.2334,0.7951) |
lnN(-2.6226,0.6972) |
lnN(-2.8233,0.6673) |
|
8. |
Коши |
lnN(-2.3228,0.8554) |
lnN(-2.6269,0.6202) |
lnN(-2.9746,0.6493) |
|
9. |
Логистическое |
lnN(-2.2460,0.8329) |
lnN(-2.8755,0.5612) |
lnN(-3.1713,0.4841) |
|
10. |
Экстремальных значений (min и max) и Вейбулла |
lnN(-2.2236,0.8369) |
lnN(-2.6077,0.6650)** |
lnN(-3.0231,0.5191) |
** - оценивался параметр формы распределения Вейбулла.
Таблица 4.
|
Предельные распределения статистики |
||||
|
№ п/п |
Распределение случайной величины |
Оценивался только масштабный параметр |
Оценивался только параметр сдвига |
Оценивалось два параметра |
|
1. |
Экспоненциальное |
lnN(-0.7055,0.5690) |
|
|
|
2. |
Полунормальное |
lnN(-0.6931,0.5900) |
|
|
|
3. |
Рэлея |
lnN(-0.6850,0.5541) |
|
|
|
4. |
Максвелла |
lnN(-0.7051,0.5658) |
|
|
|
5. |
Лапласа |
lnN(-0.4107,0.7170) |
lnN(-0.6654,0.5345) |
lnN(-0.9378,0.4999) |
|
6. |
Нормальное |
lnN(-0.4121,0.7206) |
lnN(-0.8363,0.5096) |
lnN(-1.0840,0.4509) |
|
7. |
Логнормальное |
lnN(-0.4092,0.6938) |
lnN(-0.6827,0.6146) |
lnN(-0.9322,0.5819) |
|
8. |
Коши |
lnN(-0.4326,0.7164) |
lnN(-0.6102,0.5737) |
lnN(-0.8815,0.5905) |
|
9. |
Логистическое |
lnN(-0.4243,0.7224) |
lnN(-0.8465,0.5109) |
lnN(-1.1685,0.4239) |
|
10. |
Экстремальных значений (min и max) и Вейбулла |
lnN(-0.4085,0.7180) |
lnN(-0.6911,0.5736) |
lnN(-1.0947,0.4457) |
** - оценивался параметр формы распределения Вейбулла.
Зависимость распределений непараметрических статистик от вида закона,
параметры которого оценивались по наблюдаемой выборке, можно наглядно
проследить на рис. 2-5, где соответственно рассматривались распределения
статистик , , 
, 
.
На этих рисунках представлены эмпирические распределения статистик при
оценивании по выборке всех параметров распределения: нормального (помечено
символом “1”), логистического (“2”), Лапласа (“3”), Коши (“4”). Символом “0”
на рисунках отмечено предельное распределение соответствующей классической
статистики (когда по выборке не оцениваются параметры).
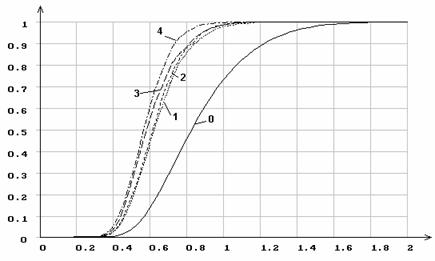
Рис. 2. Распределения статистики Колмогорова при оценивании по выборке всех параметров
распределения: 1 - нормального; 2 - логистического; 3 - Лапласа; 4 - Коши; 0
- функция распределения Колмогорова .
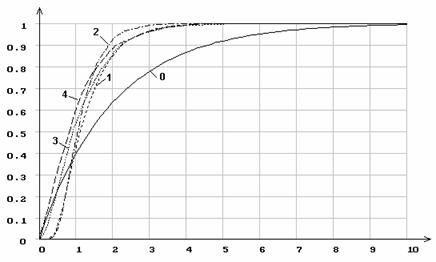
Рис. 3. Распределения статистики Смирнова при оценивании по выборке всех параметров
распределения: 1 - нормального; 2 - логистического; 3 - Лапласа; 4 - Коши; 0
- функция распределения 
.
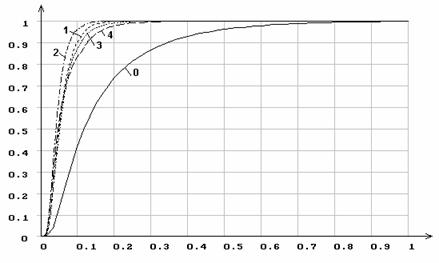
Рис. 4. Распределения статистики Мизеса при оценивании по выборке всех параметров
распределения: 1 - нормального; 2 - логистического; 3 - Лапласа; 4 - Коши; 0
- функция распределения 
.
В случае оценивания одного из параметров наблюдаемого закона (нормального,
логистического, Лапласа, Коши) распределения статистик отличны от тех, что
изображены на рис. 1-4. Предельные распределения статистик для этих законов
случайных величин зависят только от вида закона, типа и числа
оцениваемых параметров. Но возможна и менее благоприятная ситуация. Например, предельные распределения статистик всех рассматриваемых
непараметрических критериев при проверке согласия наблюдаемой выборки с
гамма-распределением зависят от значения его параметра формы . На рис. 6 представлены полученные
в результате моделирования эмпирические функции распределения статистики Колмогорова
при одновременном оценивании по выборке двух параметров гамма-распределения в
зависимости от значения параметра формы . Отметим, что с его ростом
предельные распределения статистик стремятся к предельным распределениям для нормального закона. Последними практически можно
пользоваться при >5.
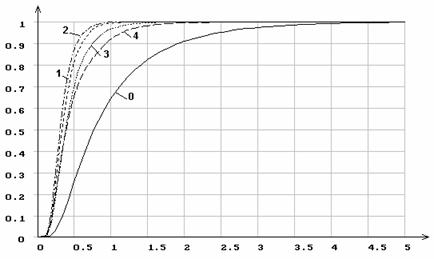
Рис. 5. Распределения статистики Мизеса при оценивании по выборке всех параметров
распределения: 1 - нормального; 2 - логистического; 3 - Лапласа; 4 - Коши; 0
- функция распределения 
.
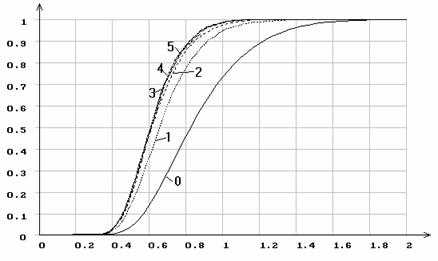
Рис. 6. Эмпирические функции распределения статистики Колмогорова при оценивании одновременно двух
параметров гамма-рапределения и различных значениях параметра формы : 0 - функция распределения Колмогорова; 1 - =0.5; 2 - =1.0;
3 - =2.0; 4 - =5.0;
5 - =10.0.
В качестве моделей законов распределения реальных случайных величин могут
использоваться и усеченные законы, и смеси законов вида 
, где 
-
параметр смеси, 
- параметры законов, входящих в смесь, в общем
случае векторные. Если по выборке будут оцениваться все или часть параметров,
определяющих смесь законов, то это отразится на предельном распределении
статистики используемого критерия. На рис. 7 для иллюстрации приведены смоделированные
распределения статистики Колмогорова при оценивании 2-х параметров нормального
распределения (“1”) и при оценивании всех 5-ти параметров смеси двух
нормальных распределений (“2”).
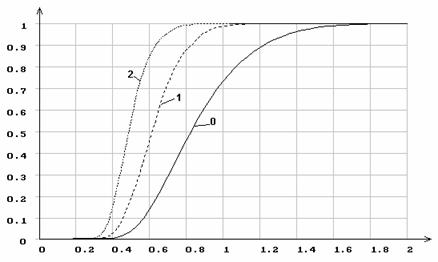
Рис. 7. Распределения статистики Колмогорова при оценивании по выборке всех параметров
распределения: 1 - нормального; 2 - смеси двух нормальных распределений (5
параметров); 0 - функция распределения Колмогорова .
Таким образом, при проверке сложных гипотез с использованием критериев
отношения правдоподобия и Пирсона
и оценивании параметров по негруппированным наблюдениям применение -распределения для вычисления вероятностей вида при асимптотически оптимальном группировании
приводит к достаточно малым ошибкам, которыми при практическом использовании
критериев можно пренебречь. А с ростом числа интервалов (
) эти ошибки оказываются малыми как при асимптотически
оптимальном, так и при равновероятном группировании. В то же время мощность
критериев при асимптотически оптимальном группировании и близких альтернативах
максимальна [4,5].
Применение законов, аппроксимирующих предельные распределения статистик
непараметрических критериев и представленных в табл. 1-4, для вычисления
вероятностей позволит делать более надежные статистические
выводы, избавит от ошибок при практическом использовании непараметрических
критериев согласия. В частности, избавит от наиболее часто совершаемых ошибок,
связанных с необоснованным принятием неверной нулевой гипотезы.
1. Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.
2.
Б.Ю.Лемешко, С.Н.Постовалов. О влиянии
способа группирования данных на распределения статистик Пирсона и отношения правдоподобия // Мат.
международной НТК “Информатика и проблемы телекоммуникаций”. - Новосибирск,
1997. - С.120-123.
3. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов. В 2-х ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. - 347 с.
4.
Лемешко Б.Ю. Асимптотически оптимальное
группирование наблюдений - это обеспечение максимальной мощности критериев //
Надежность и контроль качества, 1997. № 5. С. (в печати).
5. Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat., 1955. V.26. - P.189-211.
6. Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория, 1985. Т. 51. №1. - С. 60-62.
7.
Бондарев Б.В. О проверке сложных
статистических гипотез // Заводская лаборатория. 1986. Т. 52. № 10. - С. 62-63.
8. Durbin J. Kolmogorov-Smirnov tests when parameters are estimated // Lect. Notes Math., 1976. V.566. - P.33-44.
9. Мартынов Г.В. Критерии омега-квадрат. - М.: Наука, 1978. - 80 с.
10. Pearson E.S.,
Hartley H.O. Biometrika tables for Statisticians. Vol. 2.
- Cambridge: University Press. 1972. - 634 p.
11. Stephens M.A. Use
of Kolmogorov - Smirnov, Cramer - von Mises and related statistics - without
extensive tables // J. R. Stat. Soc., 1970. B.32. -
P.115-122.
12. Stephens M.A. EDF
statistics for goodness of fit and some comparisons // J. Am. Statist. Assoc., 1974. V.69. - P.730-737.
13. Chandra M.,
14. Тюрин Ю.Н. О предельном распределении статистик Колмогорова-Смирнова для сложной гипотезы / Известия АН СССР. Сер. Матем. 1984. Т. 48. № 6. - С. 1314-1343.
15. Тюрин Ю.Н., Саввушкина Н.Е. Критерий согласия для распределения Вейбулла-Гнеденко / Известия АН СССР. Сер. Техн. кибернетика. 1984. № 3. - С. 109-112.
16. Тюрин Ю.Н. Исследования по непараметрической статистике (непараметрические методы и линейная модель). Автореф. дисс. докт. физ.-мат. наук. - М.: МГУ, 1985. - 33 с.
17. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. - М.: ИНФРА-М, Финансы и статистика, 1995. - 384 с.
18. Саввушкина Н.Е. Критерий Колмогорова-Смирнова для логистического и гамма-распределения // Сб. тр. / ВНИИ систем. исслед. - 1990. № 8. - С. 50-56.
19. Б.Ю.Лемешко, С.Н.Постовалов. О распределениях статистик непараметрических критериев при потере свойства “свободы от распределения” // Мат. международной НТК “Информатика и проблемы телекоммуникаций”. - Новосибирск, 1997. - С. 117-120.
20. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.
21. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. - Новосибирск: Изд-во НГТУ. - 1995. - 125 с.