См. также: Прикладная математическая статистика (материалы к семинарам)

Методы менеджмента качества. Надежность и контроль качества. - 1999. № 11. - C. 34-43.

 

УДК 519.2

 

О ПРАВИЛАХ ПРОВЕРКИ СОГЛАСИЯ ОПЫТНОГО РАСПРЕДЕЛЕНИЯ С ТЕОРЕТИЧЕСКИМ

 

Б.Ю. Лемешко,  С.Н. Постовалов

 

            Целью первичной обработки экспериментальных наблюдений обыч­но является выбор закона распределения, наиболее хорошо опи­сывающего случайную величину, выборку которой мы наблюдали. Проверка того, на­сколько хорошо наблюдаемая выборка описывается теоретическим зако­ном, осуществляется с использованием различных кри­те­риев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретиче­ским является стремление удостовериться в том, что данная модель теоре­тического закона не противоречит наблю­даемым данным и использование ее не приведет к существенным ошиб­кам при вероятностных расчетах. Не­корректное исполь­зование крите­риев согласия может приводить к необос­нованному принятию (чаще всего) или необоснованному отклонению про­веряемой гипотезы.

            Существующие в различных источниках рекомендации по правилам использования критериев согласия имеют ряд очень крупных недостатков. В случае параметрических критериев типа  это связано с подходом к группированию данных, а в случае непараметрических критериев типа Колмогорова, Смирнова,  и  Мизеса – с проверкой сложных гипотез.

В действующих регламентирующих документах и, в частности, в ГОСТе СТ СЭВ 1190-78 “Прикладная статис­тика. Правила проверки согла­сия опытного распределения с теоретическим” практически не оговорены правила при­мене­ния критериев согласия при проверке сложных гипотез. Вследствие этого практика использования таких кри­териев в задачах кон­троля качества, исследования надежности и в других приложениях зача­стую приводит к некорректному их применению и, как следствие, неверным выводам. Это касается как критериев согласия типа , так и непараметри­ческих критериев типа Колмогорова или типа  Мизеса.

В критериях типа  наиболее неопределенным моментом является способ группирования данных (способ разбиения области определения слу­чай­ной величины на интервалы). В действующих рекомендациях по при­ме­нению критериев типа  используемые способы груп­пирования наблюде­ний не учитывают асимптотических свойств этого критерия. Неоднознач­ность процедуры группирования отражается на мощности применяемого критерия, его способности различать близкие гипотезы. Не учет этих свойств, как правило, приводит на практике к неоправданному принятию проверяемой гипотезы.

Пробел в руководящих документах, связанный с неэффективным и некорректным применением критериев типа , призван ликвидировать проект нового ГОСТа “Прикладная статистика. Правила проверки согла­сия опытного распределения с теоретическим. Методические рекоменда­ции. Часть I. Критерии типа ”. Проект, в основу которого положена ра­бота [1], подготовлен при поддержке Технического комитета по стандарти­зации ТК 125 “Стан­дар­тизация статистических методов управления ка­чеством”. В настоящий момент ТК 125 проводит экспертизу проекта.

Подготовленные рекомендации предназначены для использования в качестве руко­водства по применению критериев согласия типа  при ста­тистичес­кой обработке результатов наблюдений в различных приложениях: анализе данных физических и технологических экспериментов, обра­ботке результатов измерений, в задачах исследования надежности, кон­троля ка­чества и т.д. Основное внимание уделено способам разбиения наблюдаемой выборки на интервалы, в частности, асимптотически оптимальному груп­пированию, обеспечивающему максимальную мощ­ность используемому критерию при близких альтернативах [2-4].

            Что касается применения непараметрических критериев согласия типа Колмогорова, Смирнова,  и  Мизеса, то здесь узким местом является проверка сложных гипотез. В данном случае подготовка соответствующих рекомендаций требует дополнительных исследований, но в настоящий мо­мент уже возможна.

            Проблема заключается в следующем. При проверке согласия разли­чают простые и сложные гипотезы. Про­стая проверяемая гипотеза имеет вид : , где  – функция распределения вероятностей, с которой проверяется согласие наблюдаемой выборки, а  – известное значение параметра (скалярного или векторного). Сложная гипотеза имеет вид : , где  – оценка параметра, вычисленная по этой же самой выборке (если оценка  вычислена по другой выборке, то гипотеза простая).

В процессе проверки по выборке вычисляется значение  статистики используемого критерия. А далее, для того, чтобы сделать вывод о том, принять или отклонить гипотезу , необходимо знать условное распреде­ление  статистики  при справедливости . И если вероятность

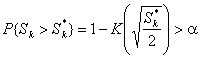
достаточно большая, по крайней мере , где  – услов­ная плотность, а  – задаваемый уровень значимости (вероятность ошибки первого рода, т.е. вероятность отклонить справедливую гипотезу ), то нет оснований отклонять гипотезу .

Когда проверяется простая гипотеза, всё ясно, и порядок проверки определен действующим СТ СЭВ 1190-78. В случае простых гипотез непа­раметрические критерии согласия Колмогорова, Смирнова,  и  Ми­зеса являются “свободными от распределения”, и условные законы распре­деления  статистик этих критериев известны.

            Так в критерии Колмогорова (Колмогорова-Смир­нова) наиболее часто ис­поль­зуется статистика [5]

,                                                      (1)

где  

 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция закона распределения, согласие с которым про­веряется. Распределение величины  при простой гипотезе в пределе подчиняется закону Колмо­горова  [5].

            Статистика критерия Смирнова [5]

                                                      (2)

при простой гипотезе в пределе подчиняется распределению  с числом степеней свободы, равным 2.

            Статистика критерия  Мизеса (Крамера-Мизеса-Смирнова)

                             (3)

при простой гипотезе подчиняется распределению  [5], а статистика критерия  Мизеса (Андерсона-Дарлинга)

      (4)

– распределению  [5].

В случае сложных гипотез, распределе­ния  существенно отли­ча­ются от распределений статистик при простых гипотезах. Более того, распре­деления статистик непараметрических критериев согласия при про­верке сложных гипотез зависят от характера этой сложной гипотезы. Це­лый ряд факторов, определяющих “сложность” гипотезы, влияет на закон распределения статистики . В первую очередь, конечно, это вид на­блюдаемого закона распределения (закона, соответ­ству­ющего истинной ги­потезе ), далее тип оцениваемого пара­метра и количество оцениваемых параметров (а в некоторых ситуациях и конкретное значение параметра, как, например, в случае гамма-рас­пре­деления), затем используемый метод оценивания параметров, а при малых объемах выборки  распределение  зависит и от . Правда существенная зависимость от  наблю­дается только при небольших объемах выборки. Уже при  рас­пределение  достаточно близко к предельному , и зависи­мостью от  можно пренебречь.

Решению проблемы применения непараметрических критериев согла­сия при сложных гипотезах с использованием различных подходов посвя­щено очень много публикаций. Главный вывод, который можно сделать на основании наиболее значимых, на наш взгляд, работ [5-18] – нельзя прене­брегать тем фактом, что проверяется сложная гипотеза: ошибки слишком велики. Однако, рекомендаций того, как поступать в каждой реальной си­туации (за редким исключением) они не дают. Специалисты по-прежнему предупреждают об опасности некорректного применения непараметриче­ских критериев при сложных гипотезах [19-21].

В [22,23] нами были получены обнадеживающие результаты при ис­сле­довании методами статистического моделирования распределе­ний ста­тистик  для различных наблюдаемых законов случайных величин и оцени­вании параметров этих законов методом максимального правдопо­добия. На основании этих результатов (построенных аппроксимаций для ) при условии, что мы фиксируем сложную гипотезу (фиксируем закон, согласие с которым проверяем, и выбираем в качестве метода оцени­вания метод максимального правдоподобия), уже можно для достаточно широкого спектра законов  обеспечивать корректное применение непарамет­рических критериев согласия.

Следует подчеркнуть, что рекомендации, вытекающие из работ [22,23], справедливы только при использовании оценок максимального правдопо­добия (ОМП). Дальнейшие исследования показали [24], что на распреде­ле­ния статистик непараметрических критериев согласия при сложных гипоте­зах очень существенно влияет приме­няемый метод оценивания параметров.

Насколько существенна зависимость распределений статистик крите­риев согласия от метода оценивания параметров показывают следующие примеры. В данном случае для иллюстрации зависимости нами использо­вались оценки максимального правдоподобия и MD-оценки. При вычисле­нии MD-оценок минимизируется соответствующее расстояние между эмпи­рическим и теорети­ческим распределениями. При использовании статис­тики Колмогорова  в качестве оценки вектора параметров  выби­раются значения, минимизирую­щие статистику (1):

 

(MD-оценки ). Аналогично, при использовании статистики  миними­зиру­ется по  статистика  (3)

(MD-оценки ).

На рис. 1 представлены распределения  статистики Колмо­го­рова  при проверке сложной гипотезы с использованием метода макси­ма­ль­­ного правдоподобия и оценивании двух параметров закона, когда ги­потезе  соответствует: “1” – нормальный закон с функцией плотности 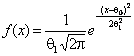, “2” – логистический 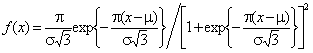, “3” – Лапласа , “4” – наименьшего значения 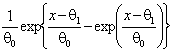, “5” – Коши .

 

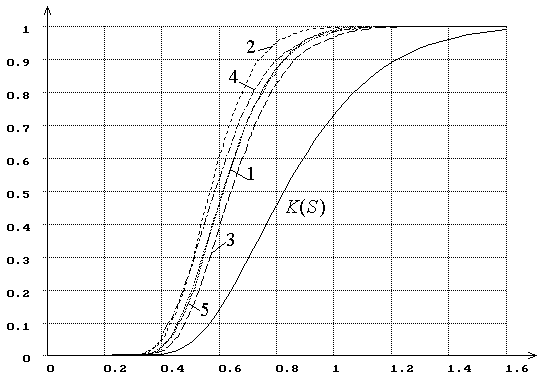
Рис. 1. Распределения  статистики Колмо­горова  при использовании ОМП.

 

            На рис. 2 для аналогичных гипотез  и использовании ОМП приве­дены распределения статистики  Крамера-Мизеса-Смирнова, а на рис. 3 в подобной ситуации - распределения статистики  Андерсона-Дарлинга. Для того, чтобы показать насколько сильно отличаются распределения  при простых и сложных гипотезах, на всех рисунках представлены графики предельных функций распределений этих статистик в случае про­верки простых гипотез, соответственно, функции распределения , , .

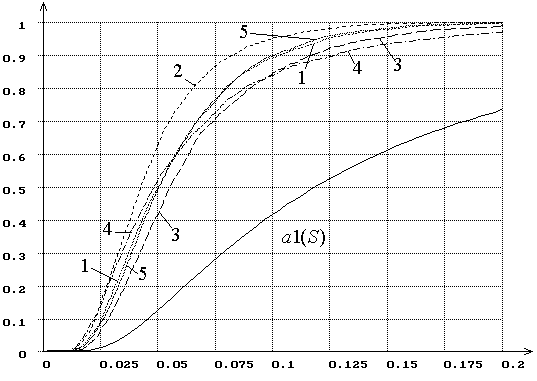
Рис. 2. Распределения  статистики  Крамера-Мизеса-Смирнова при использовании ОМП.

 

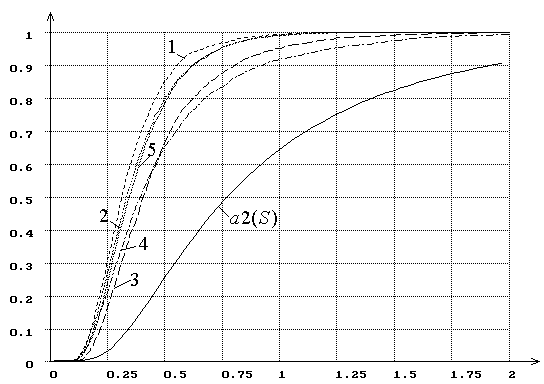
Рис. 3. Распределения  статистики  Андерсона-Дарлинга при использовании ОМП.

 

            Рис. 4 дает представление о характере изменения распределения  при одном и том же виде гипотезы :  в зависи­мости от выбранного метода оценивания. На этом рисунке приведены рас­пределения статистики  Андерсона-Дарлинга при проверке гипотезы о нормальности при использовании MD-оценок  (на рис. обозначено “1”), ОМП (“2”), MD-оценок  (“3”).

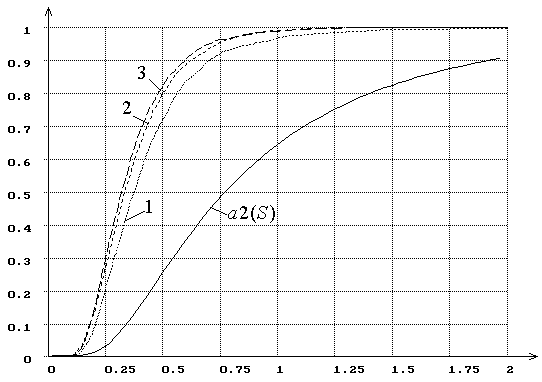
Рис. 4. Распределения  статистики  Андерсона-Дарлинга при проверке нормальности и использовании MD-оценок  (1), использовании ОМП (2), использовании MD-оценок  (3).

 

            Используемый метод оценивания очень сильно влияет на распределе­ния статистик непараметрических критериев, и не учитывать этого ни в коем случае нельзя. В то же время следует отметить, что, если при проверке гипотез :  относительно различных законов  ис­пользуются в качестве оценок параметров значения, минимизирующие ста­тистику критерия согласия, то разброс распределений  для различ­ных гипотез мини­мален. На рис. 5 представлены графики распределений  для статистики Колмогорова  при проверке тех же гипотез, что и на рис. 1 (о принад­леж­ности нормальному закону – “1”, логистическому – “2”, Лапласа – “3”, наи­меньшего значения – “4”, Коши – “5”), но при ис­пользовании в данном случае MD-оценок, ми­ни­мизирующих статистику . На рис. 6 отображены распределения  для статистики  Кра­мера-Мизеса-Смирнова для аналогичных гипотез  и использовании MD-оценок, минимизирующих эту же статистику  (сравните с рис. 2).

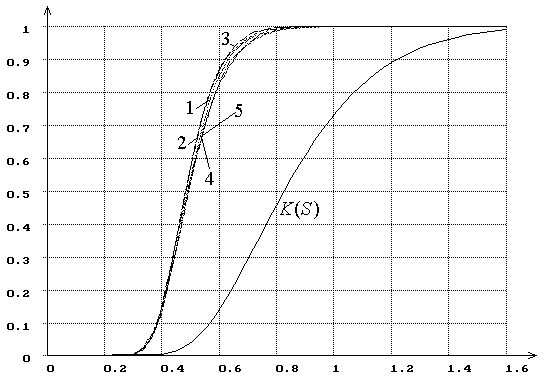
Рис. 5. Распределения  статистики Колмо­горова  при использовании MD-оценок .

 

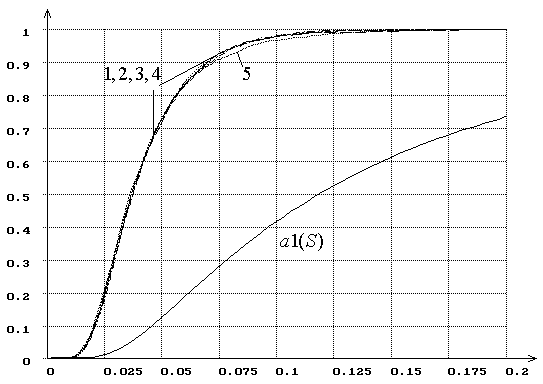
Рис. 6. Распределения  статистики   Крамера-Мизеса-Смирнова при использовании MD-оценок .

 

            Если рассматривать только распределения  статистик непа­раметрических критериев согласия, то кажется наиболее целесообразным при проверке сложных гипотез использовать MD-оценки, так как в этом случае разброс  для разных законов  минимален. Но если обратить внимание на мощность соответствующих критериев согласия, то оказывается, что следует отдать предпочтение использованию ОМП. На рис. 7 представлены оперативные характеристики (мощность  как функция от уровня значимости ) для критерия согласия Колмогорова при проверке сложной гипотезы о нормальности наблюдаемого закона против гипотезы о принадлежности выборки логистическому распределению. Опе­ративные характеристики построены для объема выборки . Они по­казывают, что при использовании ОМП критерий согласия более мощен, чем при использовании MD-оценок.

 

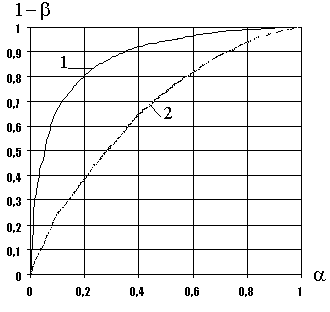
Рис.7. Оперативные характеристики критерия Колмогорова при проверке  сложной гипотезы о согласии с нормальным распределением против  альтернативы– логистическое распределение (1 – ОМП, 2 – MD-оценки)

 

            Что следует отметить в заключение? Давно назрела необходимость разработки рекомендаций, устанавливающих четкие правила применения непараметрических критериев при проверке сложных гипотез о согласии опытного распределения с теоретическим. В настоящий момент для этого уже нет принципиальных трудностей. Для достаточно широкого класса па­ра­метри­ческих моделей законов распределений, наиболее часто используе­мых в приложениях и, в частности, в задачах контроля качества и исследо­ваниях надежности, методами компьютерного моделирования могут быть построены хорошие приближения предельных распределений статистик критериев при различных сложных гипотезах (и различных методах оцени­вания). Могут быть построены аналитически простые модели и рассчитаны таблицы этих распределений, облегчающие применение критериев.

            Естественно, что при всей широте такие рекомендации не могут охва­тить всего много­обра­зия законов случайных величин, с которыми мы мо­жем столкнуться на прак­тике. В принципе, любой исследователь для кон­кретной наблюдаемой величины может предложить (построить) свою па­раметрическую модель закона, не представленную в руководящих докумен­тах, наиболее адекватно, с его точки зрения, описывающего эту случайную величину. После оценки по имеющейся выборке параметров модели возни­кает необходимость проверки сложной гипотезы об адекватности выбо­рочных наблюдений и построенного закона с использованием критериев согласия.

            Понятно, что множество всех сложных гипотез бесконечно и заранее иметь распределения  для любой сложной гипотезы  практиче­ски невозможно. Что же делать, если для описания выборки используется закон распределения вероятностей  и найдены оценки его пара­метров, а для проверки сложной гипотезы :  исследо­ва­телю неизвестно распределение  статистики соответству­ющего критерия согласия?

            Для ситуаций, когда используемый закон распределения вероятностей  и/или метод оценивания его параметров не зафиксированы кон­кретно в правилах, определяемых рекомендациями, для проверки сложной гипотезы :  наиболее целесообразно, на наш взгляд, ого­ворить в тексте руководящего документа следующую методику компьютер­ного анализа статистических закономерностей. В соответствии с законом  следует смоделировать  выборок того же объема , что и вы­борка, для которой необходимо проверить гипотезу : . Для каждой из  выборок вычислить оценки тех же параметров, а затем значение статистики  соответствующего критерия согласия. В результате получим выборку значений статистики с законом распределе­ния  для проверяемой гипотезы . По этой выборке при доста­точно большом  можно построить достаточно гладкую эмпирическую функцию распределения , которой можно непо­средственно вос­пользоваться для вывода о том, следует ли принимать гипотезу . А можно, при желании, по  построить приближенную анали­ти­ческую модель, аппрокси­ми­рующую , и тогда уже, опираясь на эту модель, принимать решение по поводу проверяемой гипотезы. Хоро­шей аналитической моделью для  может оказаться и функция распре­деления одного из знакомых законов, часто используемых в прило­жениях, как было получено в [23]. Во всяком случае, всегда можно, опи­раясь на огра­ниченное множество законов распределения, построить для  модель в виде смеси законов [ 25,26].

Реализация такой процедуры компьютерного анализа распределений статистик в настоящий момент не содержит ни принципиальных, ни прак­тических трудностей.

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

 

1.    Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статис­тика. Правила про­верки согласия опытного распределения с тео­ретическим. Мето­дические реко­мендации. Часть I. Критерии типа  . - Новосибирск: Изд-во НГТУ, 1998. - 126 с.

2.    Лемешко Б.Ю. Асимптотически оптимальное группирование наблю­де­ний - это обес­печение максимальной мощности критериев // Надеж­ность и контроль качества. - 1997. - № 8. - С. 3-14.

3.    Лемешко Б.Ю. Асимптотически оптимальное группирование наблю­дений в крите­риях согласия // Заводская лаборатория. - 1998. Т. 64. – №1. – С.56-64.

4.    Лемешко Б.Ю., Постовалов С.Н. О зависимости предельных распреде­лений ста­тис­тик  Пирсона и отношения правдоподобия от способа группирования данных // Заводская лаборатория. - 1998. Т. 64. – № 5. – С.56-63.

5.    Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

6.    Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat., 1955. V.26. - P.189-211.

7.    Durbin J.  Kolmogorov-Smirnov test when parameters are estimated  // Lect. Notes Math. 1976. V. 566. P. 33-44.

8.    Мартынов Г.В. Критерии омега-квадрат. – М.: Наука, 1978. – 80 с.

9.    Pearson E.S., Hartley H.O. Biometrica tables for Statistics. V.2. – Cambridge: University Press, 1972. – 634 p.

10.Stephens M.A. Use of Kolmogorov-Smirnov, Cramer - von Mises and related statistics – vithout extensive table // J. R. Stat. Soc., 1970, B. 32. – P. 115-122.

11.Stephens M.A. EDF statistics for goodness of fit and some comparisons // J. Am. Statist. Assoc., 1974, v.69. – P. 730-737.

12.Chandra M., Singpurwalla N.D., Stephens M.A. Statistics for Test of Fit for the Extrem-Value and Weibull Distribution // J. Am. Statist. Assoc., 1981, v.76. – P. 375.

13.Несененко Г.А. Тюрин Ю.Н. Асимптотика статистики Колмогорова для параметри­ческого семейства // ДАН СССР, 1978, т.239, № 6. – С. 1292-1294.

14.Тюрин Ю.Н. О предельном распределении статистик Колмогорова-Смирнова для сложной гипотезы // Изв. АН СССР. Сер. Матем., 1984, т. 48, № 6. – C. 1314-1343.

15.Тюрин Ю.Н., Саввушкина Н.Е. Критерии согласия для распределения Вейбулла-Гнеденко. // Изв. АН СССР. Сер. Техн. кибернетика, 1984, № 3. – C. 109-112.

16.Тюрин Ю.Н. Исследования по непараметрической статистике (непа­раметрические методы и линейная модель). Автореф. дисс. на соиск. учен. степени д-ра физ.-мат. наук. – М., 1985. - 33 с. – (МГУ).

17.Саввушкина Н.Е. Критерий Колмогорова-Смирнова для логистического и гамма-распределения // Сб. тр. ВНИИ систем. исслед. – 1990, № 8.

18.Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. // М.: ИНФРА-М, Фи­нансы и статистика, 1995. – 384 с.

19.Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория, 1985. Т. 51. №1. - С. 60-62.

20.Бондарев Б.В.  О проверке сложных статистических гипотез // Заводская лаборато­рия. 1986. Т. 52. № 10. - С. 62-63.

21.Кулинская Е.В., Саввушкина Н.Е. О некоторых ошибках в реализации и применении непараметрических методов в пакете для IBM PC // Заводская лаборатория, 1990. Т. 56. № 5. - С. 96-99.

22.Лемешко Б.Ю. Постовалов С.Н. Прикладные аспекты использования критериев со­гласия в случае проверки сложных гипотез // Надеж­ность и контроль качества. - 1997. - № 11. - С. 3-17.

23.Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непара­метрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. - 1998. Т. 64. – № 3. – С. 61-72

24.Лемешко Б.Ю., Постовалов С.Н. Исследование допредельных распре­делений ста­тистик критериев согласия при проверке сложных гипотез // Тр. IV межд. конферен­ции “Актуальные проблемы элек­трон­ного приборостроения АПЭП-98”. Новоси­бирск, 1998. Т.3. – С. 12-16.

25.Лемешко Б.Ю., Постовалов С.Н. Статистический анализ смесей рас­пре­делений по частично группированным данным // Сб. научных тру­дов НГТУ. - Новосибирск: Изд-во НГТУ, 1995. - № 1. - С. 25-31.

26.Лемешко Б.Ю., Постовалов С.Н. Программное обеспечение статис­ти­че­ского ана­лиза смесей случайных величин, пред­став­ленных частично группированными и ин­тер­вальными выборками // Тр. III межд. конференции “Актуальные проблемы элек­тронного приборо­строения АПЭП-96”. - Новосибирск, 1996. - Т. 6. - Ч.1. - С.50-53.

 

 

[Содержание]