См. также: Прикладная математическая статистика (материалы к семинарам)

Методы менеджмента качества. 2001. - № 4. - С.32-38.

УДК 519.2 

ОБ ОЦЕНИВАНИИЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ И ПРОВЕРКЕ ГИПОТЕЗ ПО ЦЕНЗУРИРОВАННЫМ ВЫБОРКАМ

Б.Ю. Лемешко

Опубликованная в ММК (НКК) № 11 за 1999 г. подборка [1-3] начинается с дискуссионной статьи О.Н. Демидовича [1], которая обоснованно концентрирует внимание на особенностях и проблемах статистического анализа в задачах надежности. В то же время статья вызывает ряд серьезных возражений, в том числе и из-за некоторого смещения акцентов в целях статистического анализа. Это касается оценки степени изученности вопросов применения критериев согласия (при проверке сложных гипотез и цензурировании данных), предложения резко ограничить число моделей законов распределения, используемых в задачах надежности, возможности различения законов распределения при цензурированных наблюдениях.

Да, статистики критериев согласия типа , типа Колмогорова и типа Мизеса известны давно. Но не все они так уж хорошо изучены и не всегда корректно применяются в приложениях, в том числе в задачах надежности. При проверке сложных гипотез далеко не всё досконально исследовано и, тем более, известно широкому кругу пользователей статистических методов, с чем, собственно говоря, и бывает связано некорректное применение данных критериев, приводящее к серьезным ошибкам.

Например, от внимания большинства исследователей, использующих критерий  Пирсона, ускользает тот факт, что мощность данного критерия падает с ростом числа интервалов группирования, и максимальную мощность критерий имеет при минимально возможном числе интервалов. Мало кому из практиков известно, что всегда можно так осуществить группировку наблюдений, чтобы обеспечить критерию  Пирсона максимальную мощность различения близких альтернатив при проверке и простых, и сложных гипотез. При проверке простых гипотез в случае применения асимптотически оптимального группирования [4,5] критерий  Пирсона превосходит по мощности критерии Колмогорова, Смирнова,  и Мизеса. Практики полностью обошли вниманием замечательный вариант критерия типа , предложенный М.С. Никулиным [6-9]. Пусть статистика этого критерия требует несколько большего объема вычислений, зато при проверке сложных гипотез и использовании оценок максимального правдоподобия по исходным негруппированным наблюдениям при любом числе оцененных параметров она подчиняется -распределению с числом степеней свободы , где  – число интервалов группирования. Ведь это, по существу, “свобода от распределения”! Этот критерий превосходит по мощности критерий  Пирсона и лишь не многим уступает по мощности в аналогичной ситуации критериям согласия типа Колмогорова и типа Мизеса.

Что касается непараметрических критериев согласия типа Колмогорова и типа Мизеса, то, к большому сожалению радикальных сторонников непараметрических методов, при проверке сложных гипотез данные критерии теряют свойство “свободы от распределения”. Распределения статистик  критериев становятся зависимыми от характера проверяемой сложной гипотезы. Причем, факт оценивания параметров и используемый метод оценивания радикально отражаются на распределениях статистик критериев. Целый ряд факторов, определяющих “сложность” гипотезы, влияет на законы распределения статистик: вид наблюдаемого закона распределения , соответствующего истинной гипотезе ; тип оцениваемого параметра и количество оцениваемых параметров; в некоторых ситуациях конкретное значение параметра; используемый метод оценивания параметров. Различных вариантов слишком много, чтобы можно было изучить распределения статистик в каждой ситуации, но это можно сделать для тех случаев, которые важны для практики. Необходимость этого может быть обоснована хотя бы тем, что при проверке сложных гипотез (в комбинации с методом максимального правдоподобия для вычисления оценок) критерии типа Колмогорова, типа  и Мизеса превосходят по мощности критерии типа . Работы [10,11] являются некоторым промежуточным итогом, опирающимся на наши результаты и результаты предыдущих авторов, однако и они покрывают лишь ограниченное множество моделей законов распределения, используемых в различных приложениях, в том числе и в теории надежности.

Должны ли статистические критерии учитывать специфику предмета, в частности, специфику задач надежности? Дело не в том, что нужны специфические критерии для задач надежности, а в том, что математическая модель должна соответствовать, быть адекватной конкретной задаче исследования надежности. А используемые математические методы должны быть корректны по отношению к виду математической модели.

Действительность всегда сложнее моделей, используемых для их описания. Любая математическая модель имеет право на жизнь и может быть использована для поиска решения, поиска оптимального решения для конкретной задачи, если эта модель адекватно отражает действительность, достаточно точно описывает и предсказывает поведение соответствующей системы. Методы оценивания параметров модели, проверка ее адекватности, проверка различных гипотез о параметрах или составляющих модели опираются (или должны опираться) на имеющуюся априорную информацию, на количество и форму (структуру) наблюдений, характеризующих поведение или состояние системы.

То же самое в задачах надежности. Специфика задач должна учитываться математической моделью. Методы обработки (методы статистического анализа) определяются математической моделью, структурой наблюдений, априорной информацией и достигнутым уровнем развития математического аппарата. Сложнее исходная задача надежности, сложнее и модель. В одних случаях наработка до отказа хорошо описывается конкретным законом распределения, в других – время жизни изделия достаточно точно задается некоторой регрессионной зависимостью и т.д. Да, никто не видел "живого" нормального, экспоненциального или любого другого распределения ни в одной задаче. Но это не мешает с использованием этих моделей описывать реальные ситуации и очень точно предсказывать возможные события.

После того, как высказаны предположения о характере вероятностной модели, на основе имеющихся наблюдений обычно решают два вида задач статистического анализа. Во-первых, стараются оценить параметры этой модели таким образом, чтобы она с наибольшей точностью описывала соответствующее явление (систему, процесс). Во-вторых, с использованием некоторого критерия проверяют адекватность модели данному явлению. Если эта модель представляет собой закон распределения, то проверка осуществляется с использованием некоторого критерия согласия. На этапе такой проверки с минимальными вероятностями ошибок гипотеза об адекватности модели должна быть принята, если это действительно так, или отклонена в пользу другой модели, более подходящей. Цель такой проверки – уловить отклонения модели от “истинной”, если они есть, а не постараться их не заметить.

Возможно с позиций реальных сроков жизни невосстанавливаемых изделий поздние отказы за пределами обычных сроков эксплуатации, вызываемые какими-либо процессами деградации, имеют достаточно малый вес в общем количестве отказов. Но если рассматривать моменты отказов как случайную величину, то модель закона распределения, если мы ее используем, должна адекватно описывать эти отказы на  всей области определения. Простые модели, наиболее часто используемые в задачах надежности (распределения экспоненциальное, Вейбулла, логарифмически нормальное, гамма-распределение), не могут описать отказы, которые на “хвостах” определяются другими технологическими факторами. В таких ситуациях достаточно хорошей моделью, описывающей действительность, может оказаться, например, смесь распределений.

Специфика задач надежности, физическая сущность конкретной предметной области, должны учитываться на этапе выбора вида модели, а методы статистического анализа должны опираться на вид модели и структуру наблюдаемых данных. В задачах надежности очень часто имеют дело с цензурированными выборками. И в этом случае, как справедливо отмечено О.Н. Демидовичем [1], проблемы налицо. Вследствие потерь информации из-за цензурирования снижается качество статистических выводов: труднее идентифицировать модель, труднее различать близкие законы распределения, снижается точность оценивания параметров. В то же время недостаточно разработаны и статистические методы анализа таких данных. Например, при вычислении по цензурированным выборкам оценок максимального правдоподобия (ОМП) сталкиваются со значительной смещённостью оценок, при этом величина смещения зависит от степени цензурирования и от объёма выборки. При цензурированных наблюдениях плохо проработаны вопросы проверки сложных гипотез о согласии эмпирического распределения с теоретическим. Конечно, при достаточно больших объёмах выборок (и достаточно большом объёме нецензурированных наблюдений) возможно применение критериев типа  (Пирсона, Никулина). При простых гипотезах и цензурированных наблюдениях для проверки согласия могут использоваться критерии Реньи [12], которые в этой ситуации являются “свободными от распределения”. Однако очевидно, что при проверке сложных гипотез они теряют это свойство и, следовательно, необходимы соответствующие исследования распределений их статистик. Отметим кстати, что в этих статистиках вполне обосновано с наибольшим весом берутся наблюдения вблизи точек цензурирования. Применимость критериев согласия типа , типа Колмогорова и типа Мизеса при цензурированных наблюдениях также требует дополнительных исследований. При этом следует иметь в виду, что как в данном случае, так и в случае критериев типа Реньи проверка сложных гипотез тесно взаимосвязана с проблемой оценивания параметров.

Нельзя согласиться с О.Н. Демидовичем по поводу уменьшения числа используемых моделей законов. То, что мы не можем различить близкие законы при цензурированных наблюдениях, не является серьезным доводом для отказа от применения множества моделей в пользу только одной. Да, при цензурировании происходят потери информации (потери информации Фишера). Это отражается на способности различать законы распределения с использованием критериев согласия и на точности оценивания параметров рассматриваемых законов. Как видим, проблемы есть, и проблемы серьезные. Но всегда ли они оказываются непреодолимыми?

Применяя критерии согласия при проверке простых гипотез, мы должны четко понимать, что, по сравнению с проверкой сложных гипотез, мощность тех же самых критериев в два, а то и в два с половиной раза меньше (при одних и тех же близких альтернативах). Ясно, что при цензурировании способность различения законов в случае простых гипотез ещё снижается. Тем более, в целях наилучшего различения законов следует осуществлять проверку сложных гипотез, оценивая по выборке параметры закона, соответствующего проверяемой гипотезе. А на этом пути следует преодолеть два препятствия, обеспечить решение двух задач. Во-первых, следует научиться на основании имеющейся (ограниченной!) информации находить по возможности наиболее точные оценки параметров. Во-вторых, требуется найти распределения статистик критериев согласия, соответствующие данному методу оценивания. Это могут быть как статистики хорошо известных старых, так и вновь предложенных критериев.

При условии, что будет реализован алгоритм эффективного решения первой задачи, решение второй не вызывает в настоящий момент принципиальных трудностей, так как с помощью методов статистического моделирования и с использованием возросших возможностей компьютерной техники с достаточной для практического применения точностью могут быть построены приближенные модели предельных распределений статистик [3,11].

Какие трудности поджидают нас при решении первой задачи? Как упоминалось выше, из-за потерь информации при цензурировании наблюдений падает точность оценивания и, самое неприятное, появляется смещение оценок, зависящее от степени цензурирования и от объёма выборок.

То, что касается возможной точности оценивания, то для ОМП скалярного параметра она ограничивается снизу асимптотической дисперсией

,

где  – объем выборки. Информационное количество Фишера по цензурированной выборке определяется соотношением

,

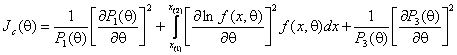где  – вероятность попадания в область цензурирования слева,  – вероятность попадания в область цензурирования справа, а наблюдаемая область лежит в пределах от  до . Если выборка цензурирована только справа, то в выражении исчезает левое слагаемое, только слева - правое слагаемое. Это соотношение позволяет судить о потерях информации о параметре распределения в зависимости от степени цензурирования слева или справа и возможной точности оценивания. Чем больше потери информации, тем меньше возможная точность оценивания.

            Очевидно, что чем больше цензурирование, тем больше потери информации. И, казалось бы, что при значительном цензурировании (при достаточно малой вероятности попадания в наблюдаемую область) ничего хорошего ожидать не следует. Однако исследования показывают, что иногда при достаточно сильном цензурировании сохраняется неожиданно много информации о параметрах закона, что дает возможность получать достаточно хорошие оценки.

Об эффективности оценивания параметров по цензурированной выборке по отношению к оцениванию по полной выборке (без цензурирования) можно судить по величине , где  – количество информации Фишера по полной выборке. В приводимой табл. 1 представлены значения  в зависимости от степени цензурирования (от величины наблюдаемой области) для распределений: экспоненциального с плотностью , Вейбулла - 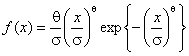, минимального значения -  и максимального -, нормального (или логарифмически нормального) - 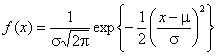, Лапласа - , Рэлея - 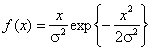, логистического - 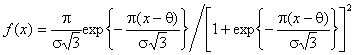, Коши - , гамма-распределения .

Таблица 1.

Отношения  для различных законов

Наблю- даемая часть %	О масштабном параметре распределений экспоненциального и Вейбулла, о параметрах сдвига распределений минимального и максимального^*) значения		О параметре формы распределения Вей булла, о параметрах масштаба распределений минимального и максимального^*) значения		О двух параметрах распределения Вейбулла, о параметрах распределений минимального и максимального^*) значения
	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа
100	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
60	0.9914	0.6000	0.7091	0.4343	0.6389	0.2658
50	0.9805	0.5000	0.6343	0.4011	0.5256	0.1771
40	0.9597	0.4000	0.5680	0.3878	0.4076	0.1093
30	0.9212	0.3000	0.5168	0.3859	0.2878	0.0595
20	0.8476	0.2000	0.4883	0.3814	0.1707	0.0257
10	0.6891	0.1000	0.4830	0.3405	0.0654	0.0063
5	0.5223	0.0500	0.4654	0.2718	0.0234	0.0015

Наблю- даемая часть %	О параметре сдвига нормального распределения	О параметре масштаба нормального распределения	О двух параметрах нормального распределения	О параметре масштаба распределения Лапласа	О параметре распределения Рэлея
	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева	Цензурирование справа
100	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
60	0.8753	0.5599	0.4399	0.6131	0.9914	0.6000
50	0.8183	0.5000	0.3296	0.6103	0.9805	0.5000
40	0.7467	0.4601	0.2311	0.5918	0.9597	0.4000
30	0.6550	0.4399	0.1457	0.5538	0.9212	0.3000
20	0.5336	0.4309	0.0754	0.4885	0.8476	0.2000
10	0.3591	0.4252	0.0239	0.3740	0.6891	0.1000
5	0.2318	0.3795	0.0073	0.2730	0.5223	0.0500

Наблю- даемая часть %	О параметре сдвига логистического распределения	О параметре масштаба логистического распределения	О двух параметрах логистического распределения	О параметре сдвига распределения Коши	О параметре масштаба распределения Коши	О двух параметрах распределения Коши
	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)	Цензурирование слева^**)
100	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
60	0.9359	0.5828	0.5249	0.9388	0.7194	0.6691
50	0.8750	0.5000	0.3917	0.9053	0.5000	0.4526
40	0.7840	0.4447	0.2679	0.7520	0.3535	0.2449
30	0.6570	0.4195	0.1603	0.4708	0.3187	0.0953
20	0.4880	0.4160	0.0754	0.1835	0.3041	0.0213
10	0.2709	0.3944	0.0199	0.0264	0.1951	0.0014
5	0.1426	0.3293	0.0051	0.0034	0.1019	0.0001

Наблю- даемая часть %	О параметре формы гамма-распределения ()		О параметре масштаба гамма-распределения ()		О двух параметрах гамма-распределения ()
	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа
100	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
60	0.6693	0.9698	0.9984	0.4750	0.4756	0.3201
50	0.5819	0.9484	0.9955	0.3715	0.3589	0.2163
40	0.4902	0.9157	0.9876	0.2778	0.2522	0.1343
30	0.3927	0.8646	0.9681	0.1939	0.1586	0.0730
20	0.2865	0.7796	0.9208	0.1196	0.0812	0.0311
10	0.1651	0.6192	0.7925	0.0554	0.0251	0.0075
5	0.0935	0.4615	0.6321	0.0265	0.0076	0.0018

Наблю- даемая часть %	О параметре формы гамма-распределения ()		О параметре масштаба гамма-распределения ()		О двух параметрах гамма-распределения ()
	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа	Цензурирование слева	Цензурирование справа
100	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
60	0.7770	0.9353	0.9759	0.6895	0.4395	0.4171
50	0.7022	0.8985	0.9548	0.5981	0.3284	0.3071
40	0.6168	0.8475	0.9208	0.5005	0.2296	0.2108
30	0.5177	0.7758	0.8659	0.3957	0.1444	0.1292
20	0.3993	0.6697	0.7737	0.2815	0.0749	0.0642
10	0.2483	0.4955	0.6002	0.1543	0.0248	0.0190
5	0.1498	0.3470	0.4369	0.0825	0.0089	0.0054

^*)  – для распределения максимального значения левое цензурирование меняется на правое;

^**)  – при левом и правом цензурировании ситуация идентична.

В случае векторного параметра в таблице приведены значения отношения определителей информационных матриц: . В зависимости от закона цензурирование справа и слева различным образом влияет на потери информации о параметрах. Конечно, данный пример представляет собой крайний случай, но при цензурировании слева, при котором вероятность попадания в наблюдаемую область составляет всего 0.05, в такой цензурированной выборке сохраняется больше 52% количества информации Фишера о параметре масштаба экспоненциального распределения!  В случае гамма-распределения величина отношения зависит от параметра формы  этого распределения и “перераспределяется” между параметрами закона с его ростом. В табл. 1 ее значения для гамма-распределения приведены для значений параметра формы 0.5 и 2. Представленные в таблице значения  позволяют ориентироваться, при какой степени цензурирования (или вероятности попадания в наблюдаемую область) при заданном объеме выборки можно надеяться оценить параметры с определенной точностью и сделать корректные выводы о результатах проверки гипотез.

Таким образом, сохраняющаяся в цензурированной выборке информация часто оказывается достаточной для оценивания параметров интересующего нас закона с требуемой точностью. Экспериментальные исследования полностью подтверждают сказанное.

Но наибольшая неприятность связана со смещенностью оценок параметров, вычисляемых по цензурированным выборкам, и, в частности, смещенностью ОМП. К тому же, при сильном цензурировании распределения ОМП параметров очень медленно сходятся к асимптотическому нормальному закону, а при ограниченных объемах выборок эти распределения оказываются существенно асимметричными. Однако обе эти проблемы не являются непреодолимыми, и имеется реальная возможность исследования законов распределения оценок (например, методами статистического моделирования), построения для вычисляемых оценок поправок на смещение в виде функций от объема выборки и степени цензурирования. Такие поправки, нейтрализующие смещение, позволят находить несмещенные оценки параметров. А возможность построения несмещенных оценок параметров по цензурированным выборкам, позволит исследовать распределения статистик критериев согласия, и, следовательно, корректно проверять сложные гипотезы относительно законов распределения.

В конечном счете, задача различения законов при цензурированных выборках не так уж безнадежна, конечно, при достаточности сохранившейся в цензурированной выборке информации.

Использование на практике полученных поправок для оценок по цензурированным наблюдениям и построенных распределений статистик критериев согласия не вызовет никаких затруднений. Но построение поправок на смещение и исследование распределений статистик критериев согласия в каждом конкретном случае представляют, сами по себе, достаточно нетривиальные и трудоемкие задачи. Поэтому выбор конкретного перечня моделей законов распределений, перспективных с точки зрения использования при исследовании надежности, для которых целесообразно построить зависимости для поправок и модели предельных распределений статистик, должен определяться специалистами, вплотную занимающимися проблемами надежности.

И еще одна ремарка. Нет ничего необычного в использовании критериев, в которых наблюдения берутся с различными весами. Однако, в контексте изложения [1] предложение “использовать для проверки согласия статистики критериев с убывающими весовыми коэффициентами для членов вариационного ряда” противоречит смыслу проверки гипотез о согласии, так как выглядит, как стремление уменьшить число случаев отклонения проверяемой гипотезы, как стремление снизить мощность критерия. Если модель неадекватна реальной ситуации, то зачем ее использовать?

В целом дискуссия, инициированная О.Н. Демидовичем на страницах журнала, несомненно, полезна. В результате может быть обозначен круг задач, обусловленных спецификой регистрации данных в задачах надежности, решение которых требует совершенствования методов статистического анализа, необходимости разработки соответствующего программного обеспечения и последующей коррекции регламентирующих документов.

Несколько замечаний по поводу статьи [2]. Строго говоря, предлагаемый в ней критерий не является критерием согласия, так как по существу проверяется гипотеза о принадлежности вектора параметров определенной области.

В основу построения этого критерия взята совместная асимптотическая нормальность оценок трех параметров. Очень сомнительно, чтобы при ограниченных объемах выборок, которыми приходится оперировать, вектор этих оценок подчинялся многомерному нормальному распределению. К сожалению, в реальных ситуациях ограниченных объемов экспериментальных данных распределения используемых статистик часто оказываются весьма далекими от асимптотических (предельных). В случае "хороших" критериев проверки гипотез распределения статистик оказывается достаточно близкими к предельным уже при объемах выборок в 15–20 наблюдений. В данном случае, повторяю, весьма сомнительна совместная нормальность оценок. Даже распределения асимптотически эффективных одномерных оценок при ограниченных объемах выборок часто оказываются достаточно далекими от нормального закона (особенно при цензурировании). Что уж говорить о совместной нормальности трехмерного вектора оценок, да при зависимости компонент?

Для упоминаемых в статье [2] законов распределений три рассматриваемых параметра не всегда являются независимыми, не будут являться независимыми и их оценки. И невозможность отличить распределение Вейбулла от нормального объясняется не близостью этих законов (с помощью других критериев эти распределения различаются обычно легко), а возможным пересечением соответствующих эллипсоидов для данных распределений.

На мой взгляд, некорректно проведено в [2] сравнение мощности критериев в пользу предлагаемого. Судя по тексту и приводимым результатам, в качестве оценок мощности взят процент отклоненных выборок, моделируемых в соответствии с распределением Вейбулла, при проверке согласия с экспоненциальным. При этом априори, по-видимому, предполагалось, что при моделировании экспоненциального распределения в 95% случаев гипотеза о согласии не будет отвергнута. Сомнительно. Тем более что невелик и материал, полученный на основании статистического моделирования. Кроме этого надо иметь в виду, что распределения статистик непараметрических критериев согласия типа Колмогорова и типа Мизеса при проверке сложных гипотез зависят от используемого метода оценивания параметров. В частности, это замечание справедливо для критерия проверки экспоненциальности, с которым проводилось сравнение. Следовательно, приводимые в [2] оценки мощности для этого критерия неверны.

СПИСОК  ИСПОЛЬЗОВАННОЙ  ЛИТЕРАТУРЫ

1. Демидович О.Н. Особенности проверки соответствия опытного распределения теоретическому в задачах надежности // Методы менеджмента качества. – 1999. – № 11. – С. 29-33.

2. Баскин Э.М. Новый общий критерий согласия // Методы менеджмента качества. – 1999. – № 11. – С. 43-55.

3. Лемешко Б.Ю. Постовалов С.Н. О правилах проверки согласия опытного распределения с теоретическим // Методы менеджмента качества. – 1999. – № 11. – С. 34-43.

4. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев // Надежность и контроль качества. - 1997. - № 8. - С. 3-14.

5. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория. - 1998. Т. 64. – №1. – С.56-64.

6. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.583-591.

7. Никулин М.С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.675-676.

8. Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // Заводская лаборатория. 1992. Т. 58. № 3. – С.52-58.

9. Aguirre N., Nikulin M. Chi-squared goodness-of-fit test for the family of logistic distributions // Kybernetika. 1994. V. 30. № 3. – P.214-222.

10. Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть I. Критерии типа  . – Новосибирск: Изд-во НГТУ. – 1998. – 126 с.

11. Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ. – 1999. – 86 с.

12. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

[Содержание]